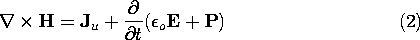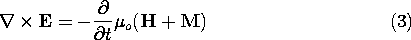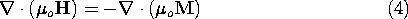12.0
Introduction

This chapter and the remaining chapters are concerned with the combined effects of the magnetic induction B / t in Faraday's law and the electric displacement current D / t in Ampère's law. Thus, the full Maxwell's equations without the quasistatic approximations form our point of departure. In the order introduced in Chaps. 1 and 2, but now including polarization and magnetization, these are, as generalized in Chaps. 6 and 9,

One may question whether a generalization carried out within the formalism of electroquasistatics and magnetoquasistatics is adequate to be included in the full dynamic Maxwell's equations, and some remarks are in order. Gauss' law for the electric field was modified to include charge that accumulates in the polarization process. The accounting for the charge leaving a designated volume was done under no restrictions of quasistatics, and thus (1) can be adopted in the fully dynamic case. Subsequently, Ampère's law was modified to preserve the divergence-free character of the right-hand side. But there was more involved in that step. The term P/ t can be identified unequivocally as the current density associated with a time dependent polarization process, provided that the medium as a whole is at rest. Thus, (2) is the correct generalization of Ampère's law for polarizable media at rest. If the medium moves with the velocity v, a term x (P x v) has to be added to the right-hand side^[1,2]. The generalization of Gauss' law and Faraday's law for magnetic fields is by analogy. If the material is moving and magnetized, a term -_o x (M x v) must be added to the right-hand side of (3). We shall not consider such moving polarized or magnetized media in the sequel.

Throughout this chapter, we are generally interested in electromagnetic fields in free space. If the region of interest is filled by a material having an appreciable polarization and or magnetization, the constitutive laws are presumed to represent a linear and isotropic material

and and are assumed uniform throughout the region of interest.

---

¹ To make any relation in this chapter apply to free space, let = _o and = _o.

---

Maxwell's equations in linear and isotropic media may be rewritten more simply

Our approach in this chapter is a continuation of the one used before. By expressing the fields in terms of superposition integrals, we emphasize the relationship between electrodynamic fields and their sources. Next we take into account the effect of conducting bodies upon the electromagnetic field, introducing the boundary value approach.

We began Chaps. 4 and 8 by expressing an irrotational E in terms of a scalar potential and a solenoidal B in terms of a vector potential A. We start this chapter in Sec. 12.1 with the generalization of these potentials to represent the electric and magnetic fields under electrodynamic conditions. Poisson's equation related to its source in Chap. 4 and A to the current density J in Chap. 8. What equation relates these potentials to their sources when quasistatic approximations do not apply? In Sec. 12.1, we develop the inhomogeneous wave equation, which assumes the role played by Poisson's equation in the quasistatic cases. It follows from this equation that for linearly polarizable and magnetizable materials, the superposition principle applies to electrodynamics.

The fields associated with source singularities are the next topic, in analogy either with Chaps. 4 or 8. In Sec. 12.2, we start with the field of an elemental charge and build up the field of a dynamic electric dipole. Here we exemplify the launching of an electromagnetic wave and see how the quasistatic electric dipole fields relate to the more general electrodynamic fields. The section concludes by deriving the electrodynamic fields associated with a magnetic dipole from the fields for an electric dipole by exploiting the symmetry of Maxwell's equations in source-free regions.

The superposition integrals developed in Sec. 12.3 provide particular solutions to the inhomogeneous wave equations, just as those of Chaps. 4 and 8, respectively, gave solutions to the scalar and vector Poisson's equations. In describing the operation of antennae, the fields that radiate away from the source are of primary interest. The superposition integrals for these radiation fields are used to find antenna radiation patterns in Sec. 12.4. The discussion of antennae is continued in Sec. 12.5, which has as a theme the complex form of Poynting's theorem. This theorem makes it possible to model the impedance of antennae as "seen" by their driving sources.

In Sec. 12.6, the field sources take the form of surface currents and surface charges. It is generally not convenient to find the associated fields by making direct use of the superposition integrals. Nevertheless, the sources are a "given," and any method that results in the associated fields amounts to solving the superposition integrals. This section provides a first view of the solutions to the wave equation in Cartesian coordinates that will be derived from the boundary value point of view in Chap. 13. In preparation for the boundary value approach of the next chapter, boundary conditions are satisfied by appropriate choices of sources. Thus, the parallel plate waveguide considered from the boundary value point of view in Chap. 13 is seen here from the point of view of waves initiated by given sources. The method of images, taken up in Sec. 12.7, provides further examples of this approach to satisfying boundary conditions.

When boundaries are introduced in this chapter, they are presumed to be perfectly conducting. In Chap. 13, the boundaries can also be interfaces between perfectly insulating dielectrics. In both of these chapters, the theme is dynamical phenomena related to the propagation and reflection of electromagnetic waves. The dynamics are characterized by one or more electromagnetic transit times, _em. Dynamical phenomena associated with charge relaxation or magnetic diffusion, characterized by _e and _m, are excluded. We will look at these again in Chaps. 14 and 15.