14.2
Transverse Electromagnetic Waves

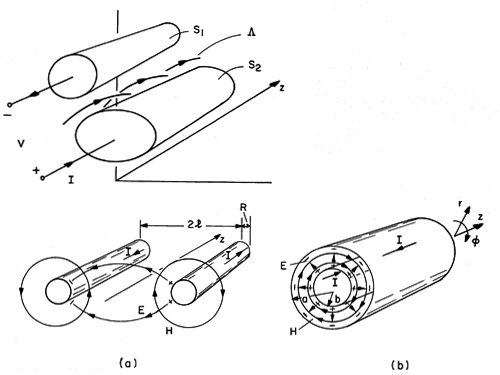
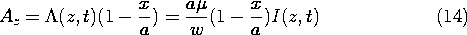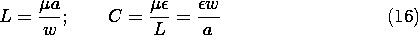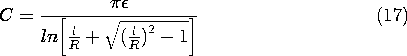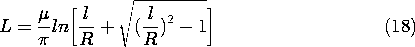The parallel plates of Sec. 13.1 are a special case of the general configuration shown in Fig. 14.2.1. The conductors have the same cross-section in any plane z = constant, but their cross-sectional geometry is arbitrary.⁴

---

⁴The direction of propagation is now z rather than y.

---

The region between the pair of perfect conductors is filled by a material having uniform permittivity and permeability . In this section, we show that such a structure can support fields that are transverse to the axial coordinate z, and that the z - t dependence of these fields is described by the ideal transmission line model.

Two common transmission line configurations are illustrated in Fig. 14.2.2.

Fig 14.2.1 and 14.2.2(top) Configuration of two parallel perfect conductors supporting TEM fields. (bottom) Two examples of transmission lines that support TEM waves: (a) parallel wire conductiors; and (b) coaxial conductors.

The TEM fields are conveniently pictured in terms of the vector and scalar potentials, A and 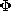, generalized to describe electrodynamic fields in Sec. 12.1. This is because such fields have only an axial component of A.

Indeed, evaluation in Cartesian coordinates, shows that even though A_z is in general not only a function of the transverse coordinates but of the axial coordinate z as well, there is no longitudinal component of H.

To insure that the electric field is also transverse to the z axis, the z component of the expression relating E to A and 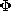(12.1.3) must be zero.

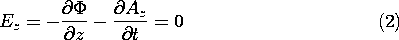
A second relation between 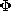and A_z is the gauge condition, (12.1.7), which in view of (1) becomes

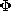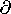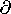These last two equations combine to show that both and A_z must satisfy the one-dimensional wave equation. For example, elimination of ² A_z/ z 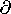t between the z derivative of (2) and the time derivative of (3) gives

A similar manipulation, with the roles of z and t reversed, shows that A_z also satisfies the one-dimensional wave equation.

Even though the potentials satisfy the one-dimensional wave equations, in general they depend on the transverse coordinates. In fact, the differential equation governing the dependence on the transverse coordinates is the two-dimensional Laplace's equation. To see this, observe that the three-dimensional Laplacian consists of a part involving derivatives with respect to the transverse coordinates and a second derivative with respect to z.

In general, 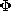and A satisfy the three-dimensional wave equation, the homogeneous forms of (12.1.8) and (12.1.10). But, in view of (4) and (5), these expressions reduce to

where the Laplacian 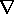²_T is the two-dimensional Laplacian, written in terms of the transverse coordinates.

Even though the fields actually depend on z, the transverse dependence is as though the fields were quasistatic and two dimensional.

The boundary conditions on the surfaces of the conductors require that there be no tangential E and no normal B. The latter condition prevails if A_z is constant on the surfaces of the conductors. This condition is familiar from Sec. 8.6. With A_z defined as zero on the surface S₁ of one of the conductors, as shown in Fig. 14.2.1, it is equal to the flux per unit length passing between the conductors when evaluated anywhere on the second conductor. Thus, the boundary conditions imposed on A_z are

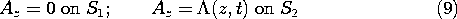
As described in Sec. 8.6, where two-dimensional magnetic fields were represented in terms of A_z, 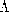is the flux per unit length passing between the conductors. Because E is transverse to z and A has only a z component, E is found from 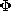by taking the transverse gradient just as if the fields were two dimensional. The boundary condition on E, met by making 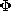constant on the surfaces of the conductors, is therefore familiar from Chaps. 4 and 5.

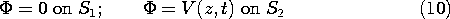
By definition, 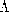is equal to the inductance per unit length L times the total current I carried by the conductor having the surface S₂.

The first of the transmission line equations is now obtained simply by evaluating (2) on the boundary S₂ of the second conductor and using the definition of 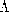from (11).

The second equation follows from a similar evaluation of (3). This time we introduce the capacitance per unit length by exploiting the relation LC = , (8.6.14).

The integral of E between the conductors within a given plane of constant z is V, and can be interpreted as the voltage between the two conductors. The total current carried in the +z direction through a plane of constant z by one of the conductors and returned in the -z direction by the other is I. Because effects of magnetic induction are important, V is a function of z. Similarly, because the displacement current is important, the current I is also a function of z.

Example 14.2.1. Parallel Plate Transmission Line

Between the perfectly conducting parallel plates of Fig. 14.1.3, solutions to (7) and (8) that meet the boundary conditions of (9) and (10) are

In the EQS context of Chap. 5, the latter is the potential associated with a uniform electric field between plane parallel electrodes, while in the MQS context of Example 8.4.4, (14) is the vector potential associated with the uniform magnetic field inside a one-turn solenoid. The inductance per unit length follows from (11) and the evaluation of (14) on the surface S₂, and one way to evaluate the capacitance per unit length is to use the relation LC = .

Every two-dimensional example from Chap. 4 with perfectly conducting boundaries is a candidate for supporting TEM fields that propagate in a direction perpendicular to the two dimensions. For every solution to (7) meeting the boundary conditions of (10), there is one to (8) satisfying the conditions of (9). This follows from the antiduality exploited in Chap. 8 to describe the magnetic fields with perfectly conducting boundaries (Example 8.6.3). The next example illustrates how we can draw upon results from these earlier chapters.

Example 14.2.2. Parallel Wire Transmission Line

For the parallel wire configuration of Fig. 14.2.2a, the capacitance per unit length was derived in Example 4.6.3, (4.6.27).

The inductance per unit length was derived in Example 8.6.1, (8.6.12).

Of course, the product of these is .

At any given instant, the electric and magnetic fields have a cross-sectional distribution depicted by Figs. 4.6.5 and 8.6.6, respectively. The evolution of the fields with z and t are predicted by the one-dimensional wave equation, (4) or (5), or a similar equation resulting from combining the transmission line equations.

Propagation is in the z direction. With the understanding that the fields have transverse distributions that are identical to the EQS and MQS patterns, the next sections focus on the evolution of the fields with z and t.

No TEM Fields in Hollow Pipes

From the general description of TEM fields given in this section, we can see that TEM modes will not exist inside a hollow perfectly conducting pipe. This follows from the fact that both A_z and 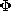must be constant on the walls of such a pipe, and solutions to (7) and (8) that meet these conditions are that A_z and 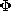, respectively, are equal to these constants throughout. From Sec. 5.2, we know that these solutions to Laplace's equation are unique. The E and H they represent are zero, so there can be no TEM fields. This is consistent with the finding for rectangular waveguides in Sec. 13.4. The parallel plate configuration considered in Secs. 13.1-13.3 could support TEM modes because it was assumed that in any given cross-section (perpendicular to the axial position), the electrodes were insulated from each other.

Power-flow and Energy Storage

The transmission line model expresses the fields in terms of V and I. For the TEM fields, this is not an approximation but rather an elegant way of dealing with a class of three-dimensional time-dependent fields. To emphasize this point, we now show the equivalence of power flow and energy storage as derived from the transmission line model and from Poynting's theorem.

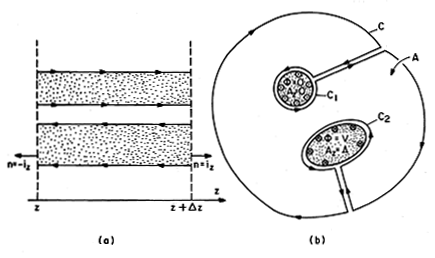
An incremental length, z, of a two-conductor system and its cross-section are pictured in Fig. 14.2.3. A one-dimensional version of the energy conservation law introduced in Sec. 11.1 can be derived from the transmission line equations using manipulations analogous to those used to derive Poynting's theorem in Sec. 11.2. We multiply (14.1.4) by V and (14.1.5) by I and add. The result is a one-dimensional statement of energy conservation.

Fig 14.2.3 Incremental length of transmission line and its cross-section.

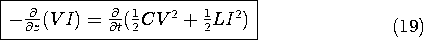
This equation has intuitive "appeal." The power flowing in the z direction is VI, and the energy per unit length stored in the electric and magnetic fields is 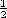CV² and 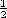LI², respectively. Multiplied by z, (19) states that the amount by which the power flow at z exceeds that at z + z is equal to the rate at which energy is stored in the length z of the line.

We can obtain the same result from the three-dimensional Poynting's integral theorem, (11.1.1), evaluated using (11.3.3), and applied to a volume element of incremental length z but one having the cross-sectional area A of the system (if need be, one extending to infinity).

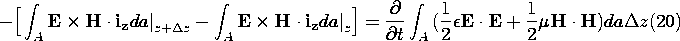
Here, the integral of Poynting's flux density, E x H, over a closed surface S has been converted to one over the cross-sectional areas A in the planes z and z + z. The closed surface is in this case a cylinder having length z in the z direction and a lateral surface described by the contour C in Fig. 14.2.3b. The integrals of Poynting's flux density over the various parts of this lateral surface (having circumference C and length z) either are zero or cancel. For example, on the surfaces of the conductors denoted by C₁ and C₂, the contributions are zero because E is perpendicular. Thus, the contributions to the integral over S come only from integrations over A in the planes z + z and z. Note that in writing these contributions on the left in (20), the normal to S on these surfaces is i_z and -i_z, respectively.

To see that the integrals of the Poynting flux over the cross-section of the system are indeed simply VI, E is written in terms of the potentials (12.1.3).

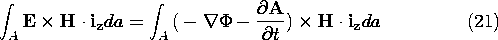
The surface of integration has its normal in the z direction. Because A is also in the z direction, the cross-product of 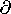A

---

/ t with H must be perpendicular to z, and therefore makes no contribution to the integral. A vector identity then converts the integral to

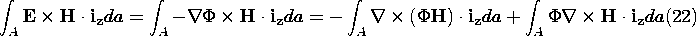
In Fig. 14.2.3, the area A, enclosed by the contour C, is insulating. Thus, because J = 0 in this region and the electric field, and hence the displacement current, are perpendicular to the surface of integration, Ampère's law tells us that the integrand in the second integral is zero. The first integral can be converted, by Stokes' theorem, to a line integral.

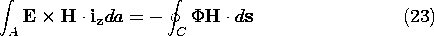
On the contour, 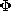= 0 on C₁ and at infinity. The contributions along the segments connecting C₁ and C₂ to infinity cancel, and so the only contribution comes from C₂. On that contour, 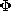= V, so 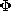is a constant. Finally, again because the displacement current is perpendicular to ds, Ampère's integral law requires that the line integral of H on the contour C₂ enclosing the conductor having potential V be equal to -I. Thus, (23) becomes

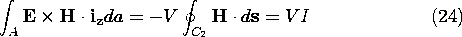
The axial power flux pictured by Poynting's theorem as passing through the insulating region between the conductors can just as well be represented by the current and voltage of one of the conductors. To formalize the equivalence of these points of view, (24) is used to evaluate the left-hand side of Poynting's theorem, (20), and that expression divided by z.

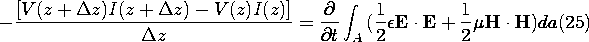
In the limit z 0, this statement is equivalent to that implied by the transmission line equations, (19), because the electric and magnetic energy storages per unit length are

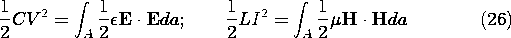
In summary, for TEM fields, we are justified in thinking of a transmission line as storing energies per unit length given by (26) and as carrying a power VI in the z direction.