15.1
Source and Material Configurations

We can use any one of a number of configurations to review physical phenomena outlined in Fig. 1.0.1. The sections, examples, and problems associated with a given physical situation are referenced in the tables used to trace the evolution of a given configuration.

Incremental Dipoles

In homogeneous media, dipole fields are simple solutions to Laplace's equation or the wave equation in two or three dimensions and have been used to represent the range of situations summarized in Table 15.1.1. As introduced in Chap. 4, the dipole represented closely spaced equal and opposite electric charges. Perhaps these charges were produced on a pair of closely spaced conducting objects, as shown in Fig. 3.3.1a. In Chap. 6, the electric dipole was used to represent polarization, and a distinction was made between unpaired and paired (polarization) charges.

TABLE 15.1.1 SUMMARY OF INCREMENTAL DIPOLES

Electroquasistatic charge: Point; Sec. 4.4, Line; Prob. 4.4.1, Sec. 5.7
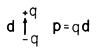Electroquasistatic polarization: Sec. 6.1
Stationary conduction current: Point; Example 7.3.2 Line; Prob. 7.3.3
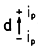Magnetoquasistatic current: Point; Example 8.3.2 Line; Example 8.1.2
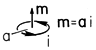Magnetoquasistatic magnetization: Sec. 9.1
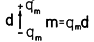Electric Electrodynamic: Point; Sec. 12.2
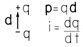Magnetic Electrodynamic: Point; Sec. 12.2

In representing conduction phenomena in Chap. 7, the dipole represented a closely spaced pair of current sources. Rather than being a source in Gauss' law, the dipole was a source in the law of charge conservation.

In magnetoquasistatics, there were two types of dipoles. First was the small current loop, where the dipole moment was the product of the area, a, and the circulating current, i. The dipole fields were those from a current loop, far from the loop, such as shown in Fig. 3.3.1b. As we will discuss in Sec. 15.2, we could have used current loop dipoles to represent magnetization. However, in Chap. 9, magnetization was represented by magnetic dipoles, a pair of equal and opposite magnetic charges. Thus, the developments of polarization in Chap. 6 were directly applicable to magnetization.

To create the time-varying positive and negative charges of the electric dipole, a current is required. In Fig. 3.3.1a, this current is supplied by the voltage source. In the EQS limit, the magnetic field associated with this current is negligible, as are the effects of the associated magnetic field. In Chap. 12, where the laws of Faraday and Ampère were made self-consistent, the coupling between these laws was found to result in electromagnetic radiation. Electric dipole radiation existed because the charging currents created some magnetic field and that, in turn, induced a rotational electric field. In the case of the magnetic dipole shown last in Table 15.1.1, electromagnetic waves resulted from a displacement current induced by the time-varying magnetic field that, in turn, produced a more rotational magnetic field.

Planar Periodic Configurations

Solutions to Laplace's equation in Cartesian coordinates are all that is required to study the quasistatic and "steady" situations outlined in Table 15.1.2. The fields used to study these physical situations, which are periodic in a plane that "extends to infinity," are by nature decaying in the direction perpendicular to that plane.

The electrodynamic fields studied in Sec. 12.6 have this same decay in a direction perpendicular to the direction of periodicity as the frequency becomes low. From the point of view of electromagnetic waves, these low frequency, essentially Laplacian, fields are represented by nonuniform plane waves. As the frequency is raised, the nonuniform plane waves become waves that propagate in the direction in which they formerly decayed. Solutions to the wave equation can be spatially periodic in both directions. The TE and TM electrodynamic field configurations that conclude Table 15.1.2 help put into perspective those aspects of the EQS and MQS configurations that do not involve losses.

TABLE 15.1.2 PLANAR PERIODIC CONFIGURATIONS  

Field Solutions   Laplace's equation:       Sec. 5.4  Wave equation:              Sec. 12.6
Electroquasistatic (EQS)  Constrained Potentials and Surface Charge:  Constrained Potentials and Volume Charge:  Constrained Potentials and Polarization:  Charge Relaxation:	Examp. 5.6.2 Examp. 5.6.1  Probs. 5.6.1-4  Probs. 6.3.1-4  Probs. 7.9.7-8
Steady Conductor (MQS or EQS)  Constrained Potential and Insulating Boundary:	Prob. 7.4.3
Magnetoquasistatic (MQS)  Magnetization:  Magnetic diffusion through Thin Conductors:	Examp. 9.3.2  Probs.10.4.1-2
Electrodynamic  Imposed Surface Sources:      Imposed Sources with Perfectly         Conducting Boundaries:    Perfectly Insulating Boundaries:	Examps. 12.6.1-2  Probs. 12.6.1-4  Examp. 12.7.2  Probs. 12.7.3-4  Probs. 13.2.1  Sec. 13.5  Probs. 13.2.3-4  Probs. 13.5.1-4

Cylindrical and Spherical

A few simple solutions to Laplace's equation are sufficient to illustrate the nature of fields in and around cylindrical and spherical material objects. Table 15.1.3 shows how a sequence of case studies begins with EQS and MQS fields, respectively, in systems of "perfect" insulators and "perfect" conductors and culminates in the very different influences of finite conductivity on EQS and MQS fields.

TABLE 15.1.3 CYLINDRICAL AND SPHERICAL CONFIGURATIONS  

Field Solutions to Laplace's Equation	Cylindrical; Sec.5.7	Spherical; Sec. 5.9
Electroquasistatic  Equipotentials: Polarization:     Permanent:       Induced: Charge Relaxation:	Examp. 5.8.1 Prob. 6.3.6  Examp. 6.6.2  Probs. 7.9.4-5	Examp. 5.9.2  Examp. 6.3.1   Prob. 6.3.5   Probs. 6.6.1-2  Examp. 7.9.3  Prob. 7.9.6
Steady Conduction (MQS or EQS) Imposed Current:	Examp. 7.5.1	Probs. 7.5.1-2
Magnetoquasistatic Imposed Current: Perfect Conductor: Magnetization: Magnetic Diffusion:	Probs. 8.5.1-2 Probs. 8.4.2-3  Probs. 9.6.3-4,10,12  Examp. 10.4.1  Probs. 10.4.5-6	Examp. 8.5.1  Examp. 8.4.3  Prob. 8.4.1 Probs. 9.6.11,13 Probs. 10.4.3-4

Fields Between Plane Parallel Plates

Uniform and piece-wise uniform quasistatic fields are sufficient to illustrate phenomena ranging from EQS, the "capacitor," to MQS "magnetic diffusion through thin conductors," Table 15.1.4. Closely related TEM fields describe the remaining situations.

TABLE 15.1.4  SPECIAL CONFIGURATIONS  

Fields Between Plane Parallel Plates      Capacitor:    Resistor:  Inductor:  Charge Relaxation:  Magnetic Diffusion though:         Thin Conductors:         Thick Conductors (TEM):  Principle (TEM) Waveguide Modes  Transmission Line:	Examps. 3.3.1, 6.3.3  Probs. 6.5.1-4, 6.6.8, 11.2.1                11.3.3, 11.6.1  Examps. 7.2.1, 7.5.2  Examp. 8.4.4, Probs. 9.5.1,3,6  Examp. 7.9.2  Prob. 10.3.4  Examps. 10.6.1, 10.7.1  Probs. 10.3.4, 10.6.1-2, 10.7.1-2  Examps. 13.1.1-2  Examps. 14.1.1, 14.8.2
Axisymmetric (Coaxial) Fields      Capacitor:  Resistor:  Inductor:  Charge Relaxation:  TEM Transmission Line	Probs 6.5.5-6  Examps. 7.5.2  Probs. 7.2.1,4,8  Examp. 3.4.1  Probs. 9.5.2,4-5  Prob. 7.9.1  Prob. 13.1.4
TM and TE Fields with Longitudinal  Boundary Conditions      Capacitive Attenuator:  TM Waveguide Fields:  Inductive Attenuator:  TE Waveguide Fields:	Sec. 5.5 Examp. 13.3.1  Examp. 8.6.3  Examp. 13.3.2
Cylindrical Conductor-Pair and  Conductor-Plane      EQS Perfect Conductors:  MQS Perfect Conductors:  TEM Transmission Line:	Examp. 4.6.3  Examp. 8.6.1  Examp. 14.2.2

Axisymmetric (Coaxial) Fields

The case studies summarized in Table 15.1.4 under this category parallel those for fields between plane parallel conductors.

TM and TE Fields with Longitudinal Boundary Conditions

The case studies under this heading in Table 15.1.4 offer the opportunity to see the relationship between fields and their sources, in the quasistatic limits and as electromagnetic waves. The EQS and MQS limits, illustrated by Demonstrations 5.5.1 and 8.6.2, respectively, become the shorted TM and TE waveguide fields of Demonstrations 13.3.1 and 13.3.2.

Cylindrical Conductor Pair and Conductor Plane

The fields used in these configurations are first EQS, then MQS, and finally TEM. The relationship between the EQS and MQS fields and the physical world is illustrated by Demonstrations 4.7.1 and 8.6.1. Regardless of cross-sectional geometry, TEM waves on pairs of perfect conductors are much of the same nature regardless of geometry, as illustrated by Demonstration 13.1.1.