Source Representation of Macroscopic Media
The primary sources of the EQS electric field intensity were the unpaired and paired charge densities, respectively, describing the influence of macroscopic media on the fields through conduction and polarization (Chap. 6). Although in Chap. 8 the primary source of the MQS magnetic field due to conduction was the unpaired current density, in Chap. 9, magnetization was modeled as the result of orientation of permanent magnetic dipoles made up of a pair of magnetic charges, positive and negative. This is not the conventional way of introducing magnetization. However, the magnetic charge model made possible an analogy between polarization and magnetization that enabled us to introduce magnetization into the field equations by analogy to polarization. More conventional is the approach that treats magnetization as the result of circulating Ampèrian currents. The two approaches lead to the same final result, only the model is different. To illustrate this, let us rewrite Maxwell's equations (12.0.1)-(12.0.4) in terms of B, rather than H

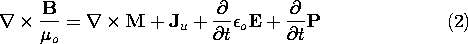


Thus, if B is considered to be the fundamental field variable,
rather than H, then the presence of magnetization manifests
itself by the appearance of the term 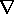 x M next to
Ju in Ampère's law. Like Ju, the Ampèrian
current density,
x M next to
Ju in Ampère's law. Like Ju, the Ampèrian
current density, 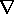 x M, is the source responsible for
driving B/
x M, is the source responsible for
driving B/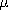 o. Because B is solenoidal, no sources of
divergence appear in Maxwell's equations reformulated in terms of
B. The fundamental source representing magnetization is now a
current flowing around a small loop (magnetic dipole). Equations
(1)-(4) are, of course, identical in content to
(12.0.1)-(12.0.4) because they resulted from the latter by a simple
substitution of B/
o. Because B is solenoidal, no sources of
divergence appear in Maxwell's equations reformulated in terms of
B. The fundamental source representing magnetization is now a
current flowing around a small loop (magnetic dipole). Equations
(1)-(4) are, of course, identical in content to
(12.0.1)-(12.0.4) because they resulted from the latter by a simple
substitution of B/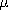 o - M for H. Yet the model of
magnetization was changed by this substitution. As mentioned in Sec.
11.8, both models lead to the same result even when relativistic
effects are included, but the Ampèrian model calls for greater
care and sophistication, because it contains moving parts (currents)
in the rest frame. This is the other reason we chose the
magnetic charge model extensively developed by L. J. Chu.
o - M for H. Yet the model of
magnetization was changed by this substitution. As mentioned in Sec.
11.8, both models lead to the same result even when relativistic
effects are included, but the Ampèrian model calls for greater
care and sophistication, because it contains moving parts (currents)
in the rest frame. This is the other reason we chose the
magnetic charge model extensively developed by L. J. Chu.
Material Idealizations
Much of our analysis of electromagnetic fields has been based on source idealizations. In the case of sources produced by or induced in media, idealizations were made of the media and of the boundary conditions implied by the induced sources. These are summarized by the first and second parts of Table 15.2.1.
| Idealization | Source Constraint | Section |
EQS Perfect Insulator Perfectly Polarized MQS Perfect "Insulator'' Perfectly Magnetized Resonant/Traveling-Wave
Electrodynamic Systems |
Charges Constrained P Constrained Currents Constrained M Constrained Self-Consistent
|
4.3-5 6.3 8.1-3 9.3 12.2-4, 12.6 |
| Idealization | Boundary Condition | Section |
EQS Perfect Conductor Steady Conduction
"Infinite'' Permeability
|
Perfectly Conducting Surfaces Equipotentials n x E n x E n x H |
4.6-7, 5.1-10 7.2, 9.6 9.6
8.4,8.6
|
The case studies listed in Tables 15.1.2-15.1.4 can be used as themes to exemplify these idealizations.
The Relativity of Perfection
We began modeling EQS and MQS fields in the presence of media by postulating "perfect" conductors. When we studied materials in more detail, we learned that "perfection" is a relative concept. Useful as are the idealizations summarized in Table 15.2.1, they must be used with proper regard for the approximations made. Those idealizations that involve conductivity depend not only on relative material properties for their validity but on size and time-rates of change as well. These are reviewed in the next section.
In each of the three "infinite parameter" idealizations listed in the table, the parameter in one region is large compared to that in another region. The appropriate boundary condition depends on the region of field excitation. The idealization makes it possible to approximate the field in an "inside" region without regard for what is "outside." One of the continuity conditions on the surface of the "inside" region is approximated as being homogeneous. Then the fields in the "outside" region are found by starting with the other continuity condition. Our first introduction to this "inside-outside" approach came in Sec. 7.5. With appropriate regard for replacing a source of curl with a source of divergence, the general discussion given in Sec. 9.6 for magnetizable materials is applicable to the other situations as well.


 0 or n . J
0 or n . J 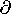 n . B/
n . B/