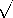Self-Consistency of Approximate Laws
By dealing with EQS and MQS systems, we concentrated on phenomena that result from approximate forms of Maxwell's equations. Terms in the "exact" equations were ignored, and field configurations were derived from these truncated forms of the equations. This way of solving problems is not unique to electromagnetic field theory. Very often it is necessary to ignore terms that appear in a "more exact" formulation of a physical problem. When this is done, it is necessary to be fully cognizant of the consequences of such approximations. Thus, the energy conservation relations used in the EQS and MQS approximations are special limiting cases of the Poynting theorem obeyed by the full Maxwell equations. The neglect of the displacement current or magnetic induction is equivalent to the neglect of the electric or magnetic energy storage.
Next, one needs to ascertain whether the problem has been sufficiently specified by the approximate form of the equations and which boundary conditions have to be retained, which discarded. The development of the EQS and MQS approximations, with the proof of the uniqueness theorem, provided examples of the development of a self-consistent formalism within the framework of a set of approximate equations. In systems composed of "perfectly conducting" and "perfectly insulating" media, it is relatively easy to decide whether or not there are subsystems that are EQS or MQS.
A system of perfect conductors surrounded by perfect insulators is likely to be EQS, if it is "open circuit" at zero frequency (a system of capacitors), and MQS, if it is "short circuit" at zero frequency (a system of inductors). However, we are generally not confronted with physical situations in which the materials are labeled as "perfect conductors" or "perfect insulators." Indeed, with the last half of Chap. 7 and Chap. 10 as background, there comes an awareness that in EQS and MQS systems the term "perfect" usually has very different meanings.
Presented with a physical object connected to an electrical source, how do we sort the dominant from the inconsequential electromagnetic phenomena? Generally, this is an iterative process with the first "guess" based on experience and intuition. With the understanding that the combinations of materials and geometries that are of practical interest are far too diverse to make a few simple rules universally applicable, this section is nevertheless aimed at organizing what we have learned so as to promote the insight required to identify dominant physical processes.
From the examination of how finite conductivity influences the distribution of the charge density in the EQS systems of Chap. 7 and the current density in the MQS systems of Chap. 10, and from the discussion of the electrodynamics of lossy materials, we have a good idea of what questions must be asked to determine the electromagnetic nature of simple subsystems. A specific example, familiar from Sec. 14.8, is the conducting block sandwiched between perfectly conducting plane parallel electrodes, shown in Fig. 14.8.1.
materials? Here this question has been reduced to, What are  ,
,  , and
, and 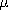 ? The most widely ranging of these parameters is the
conductivity
? The most widely ranging of these parameters is the
conductivity  , which can vary from 10-14 S/m in common
hydrocarbon liquids to almost 108 S/m in copper. Indeed,
vacuum and superconducting materials extend this range from absolute
zero to infinity.
, which can vary from 10-14 S/m in common
hydrocarbon liquids to almost 108 S/m in copper. Indeed,
vacuum and superconducting materials extend this range from absolute
zero to infinity.
Perhaps the system is driven by a sinusoidally varying source. Then,
the time scale would most likely be the reciprocal of the angular
frequency 1/ . In common engineering practice, frequencies
range from 10-2 Hz used to characterize insulation to optical
frequencies in the range of 1015 Hz. Again, nature provides
frequencies that range even more widely, including the reciprocal of
millions of years for terrestrial magnetic fields in one extreme and
the frequencies of gamma rays in the other.
. In common engineering practice, frequencies
range from 10-2 Hz used to characterize insulation to optical
frequencies in the range of 1015 Hz. Again, nature provides
frequencies that range even more widely, including the reciprocal of
millions of years for terrestrial magnetic fields in one extreme and
the frequencies of gamma rays in the other.
Similitude and Maxwell's Equations
Consider an arbitrary system, shown in Fig. 15.3.1, having the typical length l and properties

where  ,
,  , and
, and 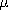 are typical magnitudes of dielectric
constant, conductivity and permeability, and
are typical magnitudes of dielectric
constant, conductivity and permeability, and 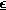 (r),
(r),  (r), and
(r), and 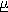 (r) are the spatial distributions,
normalized so that their peak values are of the order of unity.
(r) are the spatial distributions,
normalized so that their peak values are of the order of unity.
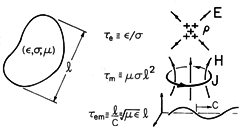
 , conductivity
, conductivity  ,
and permeability
,
and permeability 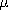 .
.
From our studies of ohmic conductors in EQS and MQS systems, we
know that field distributions are governed by the charge
relaxation time  e and the magnetic diffusion time
e and the magnetic diffusion time  m,
respectively.
Moreover, from our study of electromagnetic waves, we know that the
transit time for an electromagnetic wave,
m,
respectively.
Moreover, from our study of electromagnetic waves, we know that the
transit time for an electromagnetic wave,  em, comes into play
with electrodynamic effects. Sections in which these three times
were exemplified are listed in Table 15.3.1. Thus, we expect to find
that in systems having one typical size scale, there are no more than
three times that determine the nature of the fields.
em, comes into play
with electrodynamic effects. Sections in which these three times
were exemplified are listed in Table 15.3.1. Thus, we expect to find
that in systems having one typical size scale, there are no more than
three times that determine the nature of the fields.
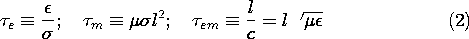
Actually, the electromagnetic transit time is the geometric mean of the other two times, so that only two of these times are independent.

TABLE 15.3.1 SECTIONS EXEMPLIFYING CHARACTERISTIC TIMES
| Electroquasistactic charge relaxation time : | Sec. 7.7, 7.9 |
| Magnetoquasistatic magnetic (current)
diffusion time: |
Sec. 10.2-7 |
| Electromagnetic wave transient time: | Sec. 12.2-7, 13.1-2, 14.3-4 |
With an excitation having the angular frequency  , the relative
distribution of sources and fields in a system is determined by the
product of
, the relative
distribution of sources and fields in a system is determined by the
product of  and any pair of these times. This can be seen by
writing Maxwell's equations in normalized form. To that end, we use
underbars to denote normalized (dimensionless) variables and normalize
the spatial coordinates to the typical length l. The time is
normalized to the reciprocal of the angular frequency.
and any pair of these times. This can be seen by
writing Maxwell's equations in normalized form. To that end, we use
underbars to denote normalized (dimensionless) variables and normalize
the spatial coordinates to the typical length l. The time is
normalized to the reciprocal of the angular frequency.
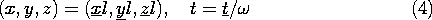
The fields and charge density are normalized to a typical electric
field intensity 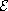 .
.
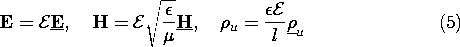
Then, Maxwell's equations (12.0.7)-(12.0.10), with the constitutive laws of (1), become

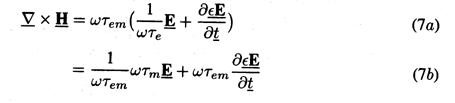
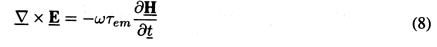

In writing the alternative forms of Ampère's law, (3) has been used.
In a system having the constitutive laws of (1), two parameters
specify the fields predicted by Maxwell's equations, (6)-(9). These
are any pair of the three ratios of the characteristic times of (2)
to the typical time of interest. For the sinusoidal steady
state, the time of interest is 1/ . Thus, using the version of
Ampère's law given by (7a), the dimensionless parameters
(
. Thus, using the version of
Ampère's law given by (7a), the dimensionless parameters
(
 em,
em, 
 e) specify the fields. Using (7b), the
parameters are (
e) specify the fields. Using (7b), the
parameters are (
 em,
em, 
 m).
m).
Characteristic Times and Lengths
Evidently, the three dimensionless parameters formed by multiplying the characteristic times of (2) by the frequency, , (or the reciprocal of some
other time typifying the dynamics), are the key to sorting out
physical processes.
, (or the reciprocal of some
other time typifying the dynamics), are the key to sorting out
physical processes.

Given two of these parameters and hence the third, we have some clues as to what physical processes are dominant. However, even in a subsystem typified by one permittivity, one conductivity, and one permeability, other parameters may be needed to specify the geometry. Every ratio of dimensions is another dimensionless parameter! To begin with, suppose that we are dealing with a system where all of the dimensions are on the order of the typical length l. The characteristic times make evident why quasistatic systems are either EQS or MQS. They also determine how the effects of finite conductivity come into play either through charge relaxation or magnetic diffusion as the frequency is raised.
Since the electromagnetic transit time is the geometric mean of
the charge relaxation and magnetic diffusion times, (3),
 em must lie between the other two times. Thus, the three times
are in one of two orders. Either
em must lie between the other two times. Thus, the three times
are in one of two orders. Either  m <
m <  e, in which case
the order of reciprocal times is as shown in Fig. 15.3.2a, or the
reverse is true, and the order is as in Fig. 15.3.2b. Moreover, if
e, in which case
the order of reciprocal times is as shown in Fig. 15.3.2a, or the
reverse is true, and the order is as in Fig. 15.3.2b. Moreover, if
 e is well removed from
e is well removed from  em, then we are assured that
em, then we are assured that
 m is also very different from
m is also very different from  em.
em.
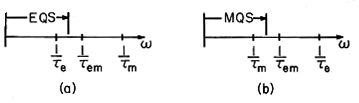
As the frequency is raised, we first encounter either the charge relaxation phenomena typical of EQS subsystems (Fig. 15.3.2a) or the magnetic diffusion phenomena of MQS subsystems (Fig. 15.3.2b). The respective quasistatic laws for EQS and MQS systems apply for frequencies ranging above the first reciprocal time but below the reciprocal electromagnetic transit time. In both cases, the frequency is well below the reciprocal of the electromagnetic delay time.
The EQS laws follow from (6)-(9) using the first form
of (7). A physical situation is characterized by the EQS laws, when
the term on the right hand side of Faraday's law, (8), is negligible.
From Ampère's law we gather that H is of the order of

 emE when
emE when 
 e > 1, and of order
(
e > 1, and of order
( em/
em/ e)E when
e)E when 
 e < 1. In the former case, in
which the displacement current density dominates over the conduction
current density, one finds for the right hand side in Faraday's law:
(
e < 1. In the former case, in
which the displacement current density dominates over the conduction
current density, one finds for the right hand side in Faraday's law:
(
 em)2E . In the latter case, in which the
conduction current density is larger than the displacement current
density, the right hand side of (8) is
em)2E . In the latter case, in which the
conduction current density is larger than the displacement current
density, the right hand side of (8) is 
 2em/
2em/ eE.
Thus the source of curl in Faraday's law can be neglected when
(
eE.
Thus the source of curl in Faraday's law can be neglected when
(
 em)2
em)2 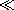 1 or
1 or 
 em/
em/ e
e 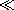 1
whichever is a more stringent limit on
1
whichever is a more stringent limit on  . The laws of EQS
prevail. An analogous, but simpler, argument arrives at the laws of
MQS. The argument is simpler, because there is no analog to
unpaired electric charge.
. The laws of EQS
prevail. An analogous, but simpler, argument arrives at the laws of
MQS. The argument is simpler, because there is no analog to
unpaired electric charge.
In cases where the ordering of characteristic times is as in Fig.
15.3.2b, the MQS laws apply for frequencies beyond the reciprocal
magnetic diffusion time but again falling short of the electromagnetic
transit time. This can be seen from the normalized Maxwell's
equations, this time using (7b). Because 
 em
em 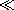 1, the last term in (7b) (the displacement current) is
negligible. Thus, we are led to the primary MQS laws, Ampère's law
with the displacement current neglected and the continuity law for
the magnetic flux density (9). This time, it follows from
Ampère's law [(7b) with the last term neglected] that H
1, the last term in (7b) (the displacement current) is
negligible. Thus, we are led to the primary MQS laws, Ampère's law
with the displacement current neglected and the continuity law for
the magnetic flux density (9). This time, it follows from
Ampère's law [(7b) with the last term neglected] that H
 (
(
 m/
m/
 em)E, so
that the right-hand side of Faraday's law, (8), is of the order
of
em)E, so
that the right-hand side of Faraday's law, (8), is of the order
of 
 m. Thus, the MQS laws are (10.0.1)-(10.0.3).
m. Thus, the MQS laws are (10.0.1)-(10.0.3).
As the frequency is raised, so that we move from left to right
along the frequency axes of Fig. 15.3.2, we expect dynamical phenomena
associated with charge relaxation, electromagnetic waves, and magnetic
diffusion to come into play as the frequency comes into the range of
the respective reciprocal characteristic times. Actually, because the
dynamics can establish their own length scales (for example, the skin
depth), matters are sometimes not so simple. However, insight is
gained by observing that the length scale l orders these critical
frequencies. With the objective of picturing the electromagnetic
phenomena in a plane, in which one axis reflects the effect of the
frequency while the other axis represents the length scale, we
normalize the frequency to the one characteristic time,  e,
that does not depend on the length. Thus, the frequency conditions
for effects of charge relaxation, magnetic diffusion, and
electromagnetic waves to be important are, respectively,
e,
that does not depend on the length. Thus, the frequency conditions
for effects of charge relaxation, magnetic diffusion, and
electromagnetic waves to be important are, respectively,

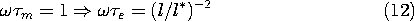
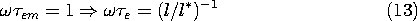
where the characteristic length l* is

In a plane in which the coordinates are essentially the length
scale and the frequency, the lines along which the frequency is equal
to the respective reciprocal characteristic times are shown in Fig.
15.3.3. The vertical axis denotes the log of the length scale
normalized to the characteristic length, while the horizontal axis is
the log of the frequency multiplied by the charge relaxation time.
Thus, the origin is where the length is equal to l* and the
frequency is equal to 1/ e.
e.
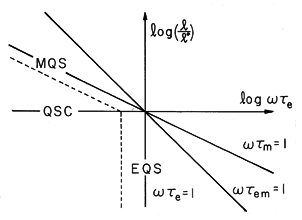
 e, the three lines denote possible boundaries between regimes.
e, the three lines denote possible boundaries between regimes.
Note that for systems having a typical length l less than the
reciprocal of the characteristic impedance conductivity product,
l*, the ordering of times is as in Fig. 15.2.1a. If the
length is greater than this characteristic length, then the ordering is
as in Fig. 15.2.1b. At least for systems having one length scale
l and one characteristic time 1/ , the system can be
MQS only if l is larger than l* and can be EQS only if l
is smaller than l*. The MQS and EQS regimes of Fig. 15.3.3 both
reduce to quasistationary conduction (QSC) at frequencies such that
, the system can be
MQS only if l is larger than l* and can be EQS only if l
is smaller than l*. The MQS and EQS regimes of Fig. 15.3.3 both
reduce to quasistationary conduction (QSC) at frequencies such that

 m
m 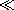 1 and
1 and 
 e
e 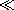 1, respectively.
1, respectively.
Since  is such a widely varying parameter, the values of
l* also have a wide range. Table 15.3.2 illustrates this fact.
In water having physiological conductivity (in flesh), the
characteristic times would coincide if the length scale were
about 12 cm at a characteristic frequency (
is such a widely varying parameter, the values of
l* also have a wide range. Table 15.3.2 illustrates this fact.
In water having physiological conductivity (in flesh), the
characteristic times would coincide if the length scale were
about 12 cm at a characteristic frequency (
 e =
1) f = 45 MHz. For lengths less than about 12 cm, the ordering
would be as in Fig. 15.3.2a and for longer lengths, as in Fig. 15.3.2b.
However, in copper it would require that the characteristic length be
less than an atomic distance to make
e =
1) f = 45 MHz. For lengths less than about 12 cm, the ordering
would be as in Fig. 15.3.2a and for longer lengths, as in Fig. 15.3.2b.
However, in copper it would require that the characteristic length be
less than an atomic distance to make  e exceed
e exceed  m. On
such a short length scale, the conductivity model is not
valid.
m. On
such a short length scale, the conductivity model is not
valid.
1 Put another way, on a time scale as short as the charge relaxation time in a metal, the inertia of the electrons responsible for the conduction would come into play. (S. Gruber, "On Charge Relaxation in Good Conductors," Proc. IEEE, Vol. 61 (1973), pp. 237-238. The inertial force is not included in the conductivity model.
In the
opposite extreme, a layer of corn oil about 60,000 miles thick would
be required to make  m exceed
m exceed  e!
e!
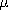 =
= 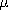 o)
o)| material |
|
|
|
l* |
| Corn oil
Water Copper |
3.1 o o
81
|
5e-11
0.2 5.7e7 |
3.5e-9
3.5e-9 1.5e-19 |
108
0.12 4.7e-11 |
Example 15.3.1. Overview of TEM Fields in Open Circuit Transmission Line Filled with Lossy Material (continued)
In Sec. 14.8, we considered the nature of the electromagnetic fields in a conductor sandwiched between "perfectly conducting" plates. Example 14.8.2 was devoted to an overview of electromagnetic regimes pictured in the length-time plane, Fig. 14.8.3, redrawn as Fig. 15.3.3. As the frequency was raised in that example with l
l*, the line
m = 1 indicated that quasi-stationary conduction had given way to magnetic diffusion (the resistor had become a system of distributed resistors and inductors). In that specific example, this was the line at which the long wave approximation broke down,
l
1. With l
l*, we have seen that as the frequency was raised, the crossing of the line
e = 1 denoted that a resistor had changed into a system of distributed resistors in parallel with distributed capacitors.
This example has a misleading simplicity that can be traced to the fact that it actually possesses more than one length scale and conductivity. To impose the TEM fields by means of the source, it was necessary to envision the slab of conductor as making perfect electrical contact with perfectly conducting plates. In reality, the boundary condition used to represent these plates implies conditions on still other parameters, notably the electrical properties and thickness of the plates.
As the frequency is raised for a system in the upper half-plane (l larger than the matching length), why do we not see a transition to electromagnetic waves at
em = 1 rather than
e = 1? The perfectly conducting plates force the displacement current to compete with the conduction current on its "own" length scale (either the skin depth or the electromagnetic wavelength). Thus, in this example, we do not make a transition from magnetic diffusion (with a penetration length determined by the skin depth
) to a damped electromagnetic wave (with a decay length of twice l*) until the electromagnetic wavelength
= 2
/

has become as short as the skin depth. Both are decreasing with increasing frequency. However, the skin depth (which decreases as 1/
) is equal to the wavelength (which decreases as 1/
) only as the frequency reaches
e = 2
2 (for present purposes, "
e = 1").
In the lower half-plane, where systems are smaller than the characteristic length, why was the transition at
e = 1 evident in the surface current density in the plates but not in the spatial distribution of the fields? The electric field was found to remain uniform until the frequency had been raised to
em = 1. Here again, the "perfectly conducting" plates obscure the general situation. The conducting block has uniform conductivity. As a result, it can support no volume charge density, regardless of the frequency. In the EQS limit, it is the charge density that shapes the electric field distribution. Here the only charges are at the interfaces between the block and the perfectly conducting plates. Until magnetic induction comes into play at
em = 1, these surface charges assume whatever distribution they must to be consistent with an irrotational electric field. As a result, the plates make the EQS fields essentially uniform, and the appropriate model simplifies to one lumped parameter C in parallel with one lumped parameter R.