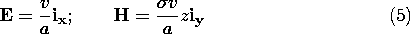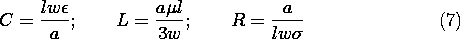Maxwell's equations attribute an excitation (E and H) to every point in space. Consistent with this view, energy density and power flow density must be associated with every point in space as well. Poynting's theorem, Sec. 11.2, does that. Poynting's theorem identifies energy storage and dissipation associated with the polarization and magnetization processes.
Each self-consistent macroscopic set of equations must possess an energy conservation principle, maybe including terms describing transformation of energy into other forms, like heat, if dissipation is present. An example was given in Sec. 11.3 of a conservation principle for the approximate description of EQS fields with a density of power flow vector that was different from E x H. This alternate form of an energy conservation principle was better suited to the EQS description, because it did not contain the H field which is not usually evaluated in the EQS approximation. Instead, the charge conservation law (derived from Ampère's law) was used to find the currents flowing in the system.
An important application of the concept of energy was the derivation of the force on macroscopic material. The force on a dielectric or magnetic object computed from energy change can include correctly the contributions to the net force from fringing fields even though the field expressions neglect them, if the energy associated with the fringing field does not change in a small displacement of the object.
Energy and Quasistatics
Because magnetic and electric energy storages, respectively, are negligible in EQS and MQS systems, a comparison of energy densities can also be used to establish the validity of a quasistatic approximation. Specifically, we will see that in systems characterized by one length scale, the ratio of magnetic to electric energy storage takes the form
where l* is the characteristic length
familiar from Secs. 14.82 and 15.3 and K is of the order of unity.
2In Sec. 14.8, twice this length was found to be the decay length for an electromagnetic wave.
Energy arguments can also be the basis for simple models that modestly extend the frequency range of quasi-stationary conduction. A second object in this section is the illustration of how these models are deduced.
As the frequency is raised, one of two processes leads to a modification in the field sources, and hence of the fields. If l is less than l*, so that 1/
e is the first reciprocal characteristic time encountered as
is raised, then the current density is progressively altered to supply unpaired charge to regions of nonuniform
and
. Alternatively, if l is larger than l*, so that 1/
Fully dynamic fields, in which all three (or more) characteristic times are of the same order of magnitude are difficult to analyze because the distribution of sources is not known until the fields have been solved selfconsistently, often a difficult task. However, if the frequency is lower than the lowest reciprocal time, the field distributions still approximate those for stationary conduction. This makes it possible to approximate the energy storages, and hence to identify both the conditions for the system to be EQS or MQS and to develop models that are appropriate for frequencies approaching the lowest reciprocal characteristic time.
The first step in this process is to determine the quasi-stationary fields. The second is to use these fields to evaluate the total electric and magnetic energy storages as well as the total energy dissipation.
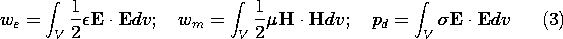
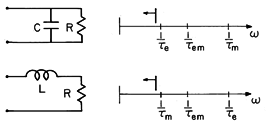
If it is found that the ratio of magnetic to electric energy storage takes the form of (1), and that if l is either very small or very large compared to the characteristic length, then we can presumably model the system by either the R-C or the L-R circuit of Fig. 15.4.1.
Fig 15.4.1 Low-frequency equivalent circuits and associated ordering to reciprocal times. As the third step, parameters in these circuits are determined by comparing we , wm, and pd, as found from the QSC fields using (3), to these quantities determined in terms of the circuit variables.
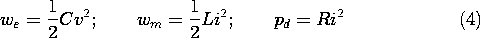
In general, the circuit models are valid only up to frequencies approaching, but not equal to, the lowest reciprocal time for the system. In the following example, we will find that the R-C circuit is an exact model for the EQS system, so that the model is valid even for frequencies beyond 1/
Example 15.4.1. Energy Method for Deriving an Equivalent Circuit
The block of uniformly conducting material sandwiched between plane parallel perfectly conducting plates, as shown in Fig. 14.8.1, was the theme of Sec. 14.8. This gives the opportunity to see how the low-frequency model developed here fits into the general picture provided by that section.
In the conducting block, the quasi-stationary conduction (QSC) fields have the distributions
The total electric and magnetic energies and total dissipation follow from an integration of the respective densities over the volume of the system in accordance with (3)
where v and i are the terminal voltage and current.
Comparison of (4) and (6) shows that
Because the entire volume of the system considered here has uniform properties, there are no sources of the electric field (charge densities) in the volume of the system. As a result, the capacitance C found here is no different than if the volume were filled with a perfectly insulating material. By contrast, if the slab were of nonuniform conductivity, as in Example 7.2.1, the capacitance, and hence equivalent circuit, found by this energy method would not be so "obvious." The inductance of the equivalent circuit does reflect a distribution of the source of the magnetic field, for the current density is distributed throughout the volume of the slab. By using the energy argument, we have acknowledged that there is a distribution of current paths, each having a different flux linkage. Strictly, when the flux linked by any current path is the same, inductance is only defined for perfectly conducting current paths.
Which equivalent circuit is appropriate? Here we decide by comparing the stored energies.
Thus, as we anticipated with (1), the system can be EQS if l
l* and MQS if l
l*. The appropriate equivalent circuit in Fig. 15.4.1 is the R-C circuit if l
The simple circuits of Fig. 15.4.1 are not generally valid if the frequency reaches the reciprocal of the longest characteristic time, since the field distributions have changed by then. In terms of the circuit elements, this means that in order for the circuits to be equivalent to the physical system, the time rates of change must remain slow enough so that
