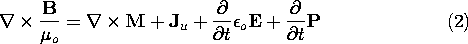In developing the study of electromagnetic fields, we have followed
the course summarized in Fig. 1.0.1. Our quest has been to make the
laws of electricity and magnetism, summarized by Maxwell's equations,
a basis for understanding and innovation. These laws are both
general and simple. But, as a consequence, they are mastered only
after experience has been gained through many specific examples. The
case studies developed in this text have been aimed at providing this
experience. This chapter reviews the examples and intends to foster
a synthesis of concepts and applications.
At each stage, simple configurations have been used to illustrate how
fields relate to their sources, whether the latter are imposed or
induced in materials. Some of these configurations are identified in
Section 15.1, where they are used to outline a comparative study of
electroquasistatic, magnetoquasistatic, and electrodynamic fields. A
review of much of the outline (Fig. 1.0.1) can be made by selecting a
particular class of configurations, such as cylinders and spheres,
and using it to exemplify the material in a sequence of case studies.
The relationship between fields and their sources is the theme in
Section 15.2. Again, following the outline in Fig. 1.0.1, electric
field sources are unpaired charges and polarization charges, while
magnetic field sources are current and (paired) magnetic charges.
Beginning with electroquasistatics, followed by magnetoquasistatics
and finally by electrodynamics, our outline first focused on physical
situations where the sources were constrained and then were induced
by the presence of media. In this text, magnetization has been
represented by magnetic charge. An alternative commonly used
formulation, in which magnetization is represented by ``Ampèrian"
currents, is discussed in Sec. 15.2.
As a starting point in the discussions of EQS, MQS, and electrodynamic
fields, we have used idealized models for media. The limits in which
materials behave as ``perfect conductors" and ``perfect insulators"
and in which they can be said to have "infinite permittivity or
permeability" provide yet another way to form an overview of the
material. Such an approach is taken at the end of Sec. 15.2.
Useful as these idealizations are, their physical significance can
be appreciated only by considering the relativity of perfection.
Although we have introduced the effects of materials by making them
ideal, we have then looked more closely and seen that ``perfection"
is a relative concept. If the fields associated with idealized
models are said to be ``zero order," the second part of Sec. 15.2
raises the level of maturity reflected in the review by considering
the ``first order" fields.
What is meant by a ``perfect conductor" in EQS and MQS systems is a
part of Sec. 15.2 that naturally leads to a review in Sec. 15.3 of how
characteristic times can be used to understand electromagnetic field
interactions with media. Now that we can see EQS and MQS systems
from the perspective of electrodynamics, Sec. 15.3 is aimed at an
overview of how the spatial scale, time scale (frequency), and material
properties determine the dominant processes. The objective in this
section is not only to integrate material, but to add insight into
the often iterative process by which a model is made to both
encapsulate the essential physics and serve as a basis of engineering
innovation.
Energy storage and dissipation, together with the associated forces
on macroscopic media, provide yet another overview of
electromagnetic systems. This is the theme of Sec. 15.4, which
summarizes the reasons why macroscopic forces can usually be
classified as being either EQS or MQS.
We can use any one of a number of configurations to review physical
phenomena outlined in Fig. 1.0.1. The sections, examples, and
problems associated with a given physical situation are referenced in
the tables used to trace the evolution of a given configuration.
Incremental Dipoles
In homogeneous media, dipole fields
are simple solutions to Laplace's equation or the wave equation in
two or three dimensions and have been used to represent the range of
situations summarized in Table 15.1.1. As introduced in Chap. 4, the
dipole represented closely spaced equal and opposite electric
charges. Perhaps these charges were produced on a pair of closely
spaced conducting objects, as shown in Fig. 3.3.1a. In Chap. 6, the
electric dipole was used to represent polarization, and a distinction
was made between unpaired and paired (polarization) charges.
 In representing conduction phenomena in Chap. 7, the dipole
represented a closely spaced pair of current sources. Rather than
being a source in Gauss' law, the dipole was a source in the law of
charge conservation.
In representing conduction phenomena in Chap. 7, the dipole
represented a closely spaced pair of current sources. Rather than
being a source in Gauss' law, the dipole was a source in the law of
charge conservation.
In magnetoquasistatics, there were two types of dipoles. First was
the small current loop, where the dipole moment was the product of
the area, a, and the circulating current, i. The dipole fields
were those from a current loop, far from the loop, such as shown in
Fig. 3.3.1b. As we will discuss in Sec. 15.2, we could have used
current loop dipoles to represent magnetization. However, in Chap.
9, magnetization was represented by magnetic dipoles, a pair of equal
and opposite magnetic charges. Thus, the developments of
polarization in Chap. 6 were directly applicable to magnetization.
To create the time-varying positive and negative charges of the
electric dipole, a current is required. In Fig. 3.3.1a, this current
is supplied by the voltage source. In the EQS limit, the magnetic
field associated with this current is negligible, as are the effects
of the associated magnetic field. In Chap. 12, where the laws of
Faraday and Ampère were made self-consistent, the coupling
between these laws was found to result in electromagnetic radiation.
Electric dipole radiation existed because the charging currents
created some magnetic field and that, in turn, induced a rotational
electric field. In the case of the magnetic dipole shown last in
Table 15.1.1, electromagnetic waves resulted from a displacement
current induced by the time-varying magnetic field that, in turn,
produced a more rotational magnetic field.
Planar Periodic Configurations
Solutions to Laplace's
equation in Cartesian coordinates are all that is required to study
the quasistatic and ``steady" situations outlined in Table 15.1.2.
The fields used to study these physical situations, which are
periodic in a plane that ``extends to infinity," are by nature
decaying in the direction perpendicular to that plane.
 The electrodynamic fields studied in Sec. 12.6 have this same decay
in a direction perpendicular to the direction of periodicity as the
frequency becomes low. From the point of view of electromagnetic
waves, these low frequency, essentially Laplacian, fields are
represented by nonuniform plane waves. As the frequency is raised,
the nonuniform plane waves become waves that propagate in the
direction in which they formerly decayed. Solutions to the wave
equation can be spatially periodic in both directions. The TE and TM
electrodynamic field configurations that conclude Table 15.1.2 help
put into perspective those aspects of the EQS and MQS configurations
that do not involve losses.
The electrodynamic fields studied in Sec. 12.6 have this same decay
in a direction perpendicular to the direction of periodicity as the
frequency becomes low. From the point of view of electromagnetic
waves, these low frequency, essentially Laplacian, fields are
represented by nonuniform plane waves. As the frequency is raised,
the nonuniform plane waves become waves that propagate in the
direction in which they formerly decayed. Solutions to the wave
equation can be spatially periodic in both directions. The TE and TM
electrodynamic field configurations that conclude Table 15.1.2 help
put into perspective those aspects of the EQS and MQS configurations
that do not involve losses.
Cylindrical and Spherical
A few simple solutions to
Laplace's equation are sufficient to illustrate the nature of fields
in and around cylindrical and spherical material objects. Table 15.1.3
shows how a sequence of case studies begins with EQS and MQS fields,
respectively, in systems of ``perfect" insulators and ``perfect"
conductors and culminates in the very different influences of finite
conductivity on EQS and MQS fields.

Fields Between Plane Parallel Plates
Uniform and
piece-wise uniform quasistatic fields are sufficient to illustrate
phenomena ranging from EQS, the ``capacitor," to MQS ``magnetic
diffusion through thin conductors," Table 15.1.4. Closely related
TEM fields describe the remaining situations.

Axisymmetric (Coaxial) Fields
The case studies
summarized in Table 15.1.4 under this category parallel those for
fields between plane parallel conductors.
TM and TE Fields with Longitudinal Boundary Conditions
The case studies under this heading in Table 15.1.4 offer
the opportunity to see the relationship between fields and their
sources, in the quasistatic limits and as electromagnetic waves. The
EQS and MQS limits, illustrated by Demonstrations 5.5.1 and 8.6.2,
respectively, become the shorted TM and TE waveguide fields of
Demonstrations 13.3.1 and 13.3.2.
Cylindrical Conductor Pair and Conductor Plane
The fields
used in these configurations are first EQS, then MQS, and finally TEM.
The relationship between the EQS and MQS fields and the physical
world is illustrated by Demonstrations 4.7.1 and 8.6.1. Regardless
of cross-sectional geometry, TEM waves on pairs of perfect conductors
are much of the same nature regardless of geometry, as illustrated by
Demonstration 13.1.1.
Self-Consistency of Approximate Laws
By dealing with EQS and MQS systems, we concentrated
on phenomena that result from approximate forms of Maxwell's
equations. Terms in the ``exact" equations were ignored, and field
configurations were derived from these truncated forms of the
equations. This way of solving problems is not unique to
electromagnetic field theory. Very often it is necessary to ignore
terms that appear in a ``more exact" formulation of a physical
problem. When this is done, it is necessary to be fully cognizant of
the consequences of such approximations. Thus, the energy
conservation relations used in the EQS and MQS approximations are
special limiting cases of the Poynting theorem obeyed by the full
Maxwell equations. The neglect of the displacement current or
magnetic induction is equivalent to the neglect of the electric or
magnetic energy storage.
Next, one needs to ascertain whether the problem has been sufficiently
specified by the approximate form of the equations and which boundary
conditions have to be retained, which discarded.
The development of the EQS and MQS approximations, with the proof of
the uniqueness theorem, provided examples of the development of a
self-consistent formalism within the framework of a set of
approximate equations. In systems composed of "perfectly
conducting" and ``perfectly insulating" media, it is relatively
easy to decide whether or not there are subsystems that are EQS or
MQS.
A system of perfect
conductors surrounded by perfect insulators is likely to be EQS, if it
is ``open circuit" at zero frequency (a system of capacitors), and
MQS, if it is ``short circuit" at zero frequency (a system of
inductors). However, we are generally not confronted with physical
situations in which the materials are labeled as "perfect
conductors" or ``perfect insulators." Indeed, with the last half
of Chap. 7 and Chap. 10 as background, there comes an awareness that
in EQS and MQS systems the term ``perfect" usually has very
different meanings.
Presented with a physical object connected to an electrical
source, how do we sort the dominant from the inconsequential
electromagnetic phenomena? Generally, this is an iterative process
with the first ``guess" based on experience and intuition.
With the understanding that the combinations of materials and
geometries that are of practical interest are far too diverse to make
a few simple rules universally applicable, this section is
nevertheless aimed at organizing what we have learned so as to
promote the insight required to identify dominant physical
processes.
From the examination of how finite conductivity influences the
distribution of the charge density in the EQS systems of Chap. 7 and
the current density in the MQS systems of Chap. 10, and from the
discussion of the electrodynamics of lossy materials, we have a good
idea of what questions must be asked to determine the electromagnetic
nature of simple subsystems. A specific example, familiar from Sec.
14.8, is the conducting block sandwiched between perfectly conducting
plane parallel electrodes, shown in Fig. 14.8.1.
materials? Here this question has been reduced to, What are  ,
,  , and
, and  ? The most widely ranging of these parameters is the
conductivity
? The most widely ranging of these parameters is the
conductivity  , which can vary from 10-14 S/m in common
hydrocarbon liquids to almost 108 S/m in copper. Indeed,
vacuum and superconducting materials extend this range from absolute
zero to infinity.
, which can vary from 10-14 S/m in common
hydrocarbon liquids to almost 108 S/m in copper. Indeed,
vacuum and superconducting materials extend this range from absolute
zero to infinity.
| \bullet | First, what are the electrical properties of the
|
| \bullet | Second, what is the size scale l? In common
engineering systems, lengths of interest range from the submicrometer
scales of semiconductor junctions to lengths for power transmission
systems in excess of 1000 kilometers. Of course, even this range is
small compared to the subnuclear to supergalactic range provided by
nature.
|
Perhaps the system is driven by a sinusoidally varying source. Then,
the time scale would most likely be the reciprocal of the angular
frequency 1/ . In common engineering practice, frequencies
range from 10-2 Hz used to characterize insulation to optical
frequencies in the range of 1015 Hz. Again, nature provides
frequencies that range even more widely, including the reciprocal of
millions of years for terrestrial magnetic fields in one extreme and
the frequencies of gamma rays in the other.
. In common engineering practice, frequencies
range from 10-2 Hz used to characterize insulation to optical
frequencies in the range of 1015 Hz. Again, nature provides
frequencies that range even more widely, including the reciprocal of
millions of years for terrestrial magnetic fields in one extreme and
the frequencies of gamma rays in the other.
Similitude and Maxwell's Equations
Consider an arbitrary system, shown in Fig. 15.3.1, having the
typical length l and properties
 where
where  ,
,  , and
, and  are typical magnitudes of dielectric
constant, conductivity and permeability, and \un
are typical magnitudes of dielectric
constant, conductivity and permeability, and \un (r), \un
(r), \un (r), and \un
(r), and \un (r) are the spatial distributions,
normalized so that their peak values are of the order of unity.
(r) are the spatial distributions,
normalized so that their peak values are of the order of unity.
 From our studies of ohmic conductors in EQS and MQS systems, we
know that field distributions are governed by the charge
relaxation time
From our studies of ohmic conductors in EQS and MQS systems, we
know that field distributions are governed by the charge
relaxation time  e and the magnetic diffusion time
e and the magnetic diffusion time  m,
respectively.
Moreover, from our study of electromagnetic waves, we know that the
transit time for an electromagnetic wave,
m,
respectively.
Moreover, from our study of electromagnetic waves, we know that the
transit time for an electromagnetic wave,  em, comes into play
with electrodynamic effects. Sections in which these three times
were exemplified are listed in Table 15.3.1. Thus, we expect to find
that in systems having one typical size scale, there are no more than
three times that determine the nature of the fields.
em, comes into play
with electrodynamic effects. Sections in which these three times
were exemplified are listed in Table 15.3.1. Thus, we expect to find
that in systems having one typical size scale, there are no more than
three times that determine the nature of the fields.
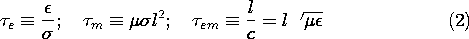 Actually, the electromagnetic transit time is the geometric mean of
the other two times, so that only two of these times are independent.
Actually, the electromagnetic transit time is the geometric mean of
the other two times, so that only two of these times are independent.

 With an excitation having the angular frequency
With an excitation having the angular frequency  , the relative
distribution of sources and fields in a system is determined by the
product of
, the relative
distribution of sources and fields in a system is determined by the
product of  and any pair of these times. This can be seen by
writing Maxwell's equations in normalized form. To that end, we use
underbars to denote normalized (dimensionless) variables and normalize
the spatial coordinates to the typical length l. The time is
normalized to the reciprocal of the angular frequency.
and any pair of these times. This can be seen by
writing Maxwell's equations in normalized form. To that end, we use
underbars to denote normalized (dimensionless) variables and normalize
the spatial coordinates to the typical length l. The time is
normalized to the reciprocal of the angular frequency.
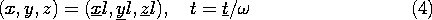 The fields and charge density are normalized to a typical electric
field intensity \cal E.
The fields and charge density are normalized to a typical electric
field intensity \cal E.
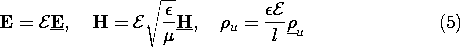 Then, Maxwell's equations (12.0.7)-(12.0.10), with the constitutive
laws of (1), become
Then, Maxwell's equations (12.0.7)-(12.0.10), with the constitutive
laws of (1), become

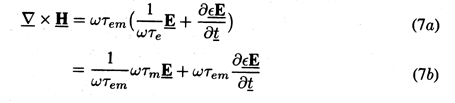
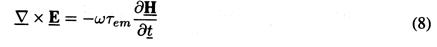
 In writing the alternative forms of Ampère's law, (3) has been used.
In writing the alternative forms of Ampère's law, (3) has been used.
In a system having the constitutive laws of (1), two parameters
specify the fields predicted by Maxwell's equations, (6)-(9). These
are any pair of the three ratios of the characteristic times of (2)
to the typical time of interest. For the sinusoidal steady
state, the time of interest is 1/ . Thus, using the version of
Ampère's law given by (7a), the dimensionless parameters
(
. Thus, using the version of
Ampère's law given by (7a), the dimensionless parameters
(
 em,
em, 
 e) specify the fields. Using (7b), the
parameters are (
e) specify the fields. Using (7b), the
parameters are (
 em,
em, 
 m).
m).
Characteristic Times and Lengths
Evidently, the three
dimensionless parameters formed by multiplying the characteristic
times of (2) by the frequency,  , (or the reciprocal of some
other time typifying the dynamics), are the key to sorting out
physical processes.
, (or the reciprocal of some
other time typifying the dynamics), are the key to sorting out
physical processes.
 Given two of these parameters and hence the third, we have some clues
as to what physical processes are dominant. However, even in a
subsystem typified by one permittivity, one conductivity, and one
permeability, other parameters may be needed to specify the geometry.
Every ratio of dimensions is another dimensionless parameter! To
begin with, suppose that we are dealing with a system where all of
the dimensions are on the order of the typical length l. The
characteristic times make evident why quasistatic systems are either
EQS or MQS. They also determine how the effects of finite
conductivity come into play either through charge relaxation or
magnetic diffusion as the frequency is raised.
Given two of these parameters and hence the third, we have some clues
as to what physical processes are dominant. However, even in a
subsystem typified by one permittivity, one conductivity, and one
permeability, other parameters may be needed to specify the geometry.
Every ratio of dimensions is another dimensionless parameter! To
begin with, suppose that we are dealing with a system where all of
the dimensions are on the order of the typical length l. The
characteristic times make evident why quasistatic systems are either
EQS or MQS. They also determine how the effects of finite
conductivity come into play either through charge relaxation or
magnetic diffusion as the frequency is raised.
Since the electromagnetic transit time is the geometric mean of
the charge relaxation and magnetic diffusion times, (3),
 em must lie between the other two times. Thus, the three times
are in one of two orders. Either
em must lie between the other two times. Thus, the three times
are in one of two orders. Either  m <
m <  e, in which case
the order of reciprocal times is as shown in Fig. 15.3.2a, or the
reverse is true, and the order is as in Fig. 15.3.2b. Moreover, if
e, in which case
the order of reciprocal times is as shown in Fig. 15.3.2a, or the
reverse is true, and the order is as in Fig. 15.3.2b. Moreover, if
 e is well removed from
e is well removed from  em, then we are assured that
em, then we are assured that
 m is also very different from
m is also very different from  em.
em.
 As the frequency is raised, we first encounter either the charge
relaxation phenomena typical of EQS subsystems (Fig. 15.3.2a) or the
magnetic diffusion phenomena of MQS subsystems (Fig. 15.3.2b). The
respective quasistatic laws for EQS and MQS systems apply for
frequencies ranging above the first reciprocal time but
below the reciprocal electromagnetic transit time. In both cases, the
frequency is well below the reciprocal of the electromagnetic delay
time.
The EQS laws follow from (6)-(9) using the first form
of (7). A physical situation is characterized by the EQS laws, when
the term on the right hand side of Faraday's law, (8), is negligible.
From Ampère's law we gather that \underlineH is of the order of
As the frequency is raised, we first encounter either the charge
relaxation phenomena typical of EQS subsystems (Fig. 15.3.2a) or the
magnetic diffusion phenomena of MQS subsystems (Fig. 15.3.2b). The
respective quasistatic laws for EQS and MQS systems apply for
frequencies ranging above the first reciprocal time but
below the reciprocal electromagnetic transit time. In both cases, the
frequency is well below the reciprocal of the electromagnetic delay
time.
The EQS laws follow from (6)-(9) using the first form
of (7). A physical situation is characterized by the EQS laws, when
the term on the right hand side of Faraday's law, (8), is negligible.
From Ampère's law we gather that \underlineH is of the order of

 em\underlineE when
em\underlineE when 
 e > 1, and of order
e > 1, and of order
 em/
em/ e when
e when 
 e < 1. In the former case, in
which the displacement current density dominates over the conduction
current density, one finds for the right hand side in Faraday's law:
(
e < 1. In the former case, in
which the displacement current density dominates over the conduction
current density, one finds for the right hand side in Faraday's law:
(
 em)2 \underlineE. In the latter case, in which the
conduction current density is larger than the displacement current
density, the right hand side of (8) is
em)2 \underlineE. In the latter case, in which the
conduction current density is larger than the displacement current
density, the right hand side of (8) is 
 2em/
2em/ e
\underlineE.
Thus the source of curl in Faraday's law can be neglected when
(
e
\underlineE.
Thus the source of curl in Faraday's law can be neglected when
(
 em)2 \ll 1 or
em)2 \ll 1 or 
 em/
em/ e \ll 1
whichever is a more stringent limit on
e \ll 1
whichever is a more stringent limit on  . The laws of EQS
prevail. An analogous, but simpler, argument arrives at the laws of
MQS. The argument is simpler, because there is no analog to
unpaired electric charge.
. The laws of EQS
prevail. An analogous, but simpler, argument arrives at the laws of
MQS. The argument is simpler, because there is no analog to
unpaired electric charge.
In cases where the ordering of characteristic times is as in Fig.
15.3.2b, the MQS laws apply for frequencies beyond the reciprocal
magnetic diffusion time but again falling short of the electromagnetic
transit time. This can be seen from the normalized Maxwell's
equations, this time using (7b). Because 
 em \ll
1, the last term in (7b) (the displacement current) is
negligible. Thus, we are led to the primary MQS laws, Ampère's law
with the displacement current neglected and the continuity law for
the magnetic flux density (9). This time, it follows from
Ampère's law [(7b) with the last term neglected] that H
\approx (
em \ll
1, the last term in (7b) (the displacement current) is
negligible. Thus, we are led to the primary MQS laws, Ampère's law
with the displacement current neglected and the continuity law for
the magnetic flux density (9). This time, it follows from
Ampère's law [(7b) with the last term neglected] that H
\approx (
 m/
m/
 em)E, so
that the right-hand side of Faraday's law, (8), is of the order
of
em)E, so
that the right-hand side of Faraday's law, (8), is of the order
of 
 m. Thus, the MQS laws are (10.0.1)-(10.0.3).
m. Thus, the MQS laws are (10.0.1)-(10.0.3).
As the frequency is raised, so that we move from left to right
along the frequency axes of Fig. 15.3.2, we expect dynamical phenomena
associated with charge relaxation, electromagnetic waves, and magnetic
diffusion to come into play as the frequency comes into the range of
the respective reciprocal characteristic times. Actually, because the
dynamics can establish their own length scales (for example, the skin
depth), matters are sometimes not so simple. However, insight is
gained by observing that the length scale l orders these critical
frequencies. With the objective of picturing the electromagnetic
phenomena in a plane, in which one axis reflects the effect of the
frequency while the other axis represents the length scale, we
normalize the frequency to the one characteristic time,  e,
that does not depend on the length. Thus, the frequency conditions
for effects of charge relaxation, magnetic diffusion, and
electromagnetic waves to be important are, respectively,
e,
that does not depend on the length. Thus, the frequency conditions
for effects of charge relaxation, magnetic diffusion, and
electromagnetic waves to be important are, respectively,

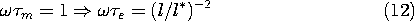
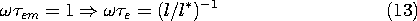 where the characteristic length l* is
where the characteristic length l* is
 In a plane in which the coordinates are essentially the length
scale and the frequency, the lines along which the frequency is equal
to the respective reciprocal characteristic times are shown in Fig.
15.3.3. The vertical axis denotes the log of the length scale
normalized to the characteristic length, while the horizontal axis is
the log of the frequency multiplied by the charge relaxation time.
Thus, the origin is where the length is equal to l* and the
frequency is equal to 1/
In a plane in which the coordinates are essentially the length
scale and the frequency, the lines along which the frequency is equal
to the respective reciprocal characteristic times are shown in Fig.
15.3.3. The vertical axis denotes the log of the length scale
normalized to the characteristic length, while the horizontal axis is
the log of the frequency multiplied by the charge relaxation time.
Thus, the origin is where the length is equal to l* and the
frequency is equal to 1/ e.
e.
 Note that for systems having a typical length l less than the
reciprocal of the characteristic impedance conductivity product,
l*, the ordering of times is as in Fig. 15.2.1a. If the
length is greater than this characteristic length, then the ordering is
as in Fig. 15.2.1b. At least for systems having one length scale
l and one characteristic time 1/
Note that for systems having a typical length l less than the
reciprocal of the characteristic impedance conductivity product,
l*, the ordering of times is as in Fig. 15.2.1a. If the
length is greater than this characteristic length, then the ordering is
as in Fig. 15.2.1b. At least for systems having one length scale
l and one characteristic time 1/ , the system can be
MQS only if l is larger than l* and can be EQS only if l
is smaller than l*. The MQS and EQS regimes of Fig. 15.3.3 both
reduce to quasistationary conduction (QSC) at frequencies such that
, the system can be
MQS only if l is larger than l* and can be EQS only if l
is smaller than l*. The MQS and EQS regimes of Fig. 15.3.3 both
reduce to quasistationary conduction (QSC) at frequencies such that

 m \ll 1 and
m \ll 1 and 
 e \ll 1, respectively.
e \ll 1, respectively.
Since  is such a widely varying parameter, the values of
l* also have a wide range. Table 15.3.2 illustrates this fact.
In water having physiological conductivity (in flesh), the
characteristic times would coincide if the length scale were
about 12 cm at a characteristic frequency (
is such a widely varying parameter, the values of
l* also have a wide range. Table 15.3.2 illustrates this fact.
In water having physiological conductivity (in flesh), the
characteristic times would coincide if the length scale were
about 12 cm at a characteristic frequency (
 e =
1) f = 45 MHz. For lengths less than about 12 cm, the ordering
would be as in Fig. 15.3.2a and for longer lengths, as in Fig. 15.3.2b.
However, in copper it would require that the characteristic length be
less than an atomic distance to make
e =
1) f = 45 MHz. For lengths less than about 12 cm, the ordering
would be as in Fig. 15.3.2a and for longer lengths, as in Fig. 15.3.2b.
However, in copper it would require that the characteristic length be
less than an atomic distance to make  e exceed
e exceed  m. On
such a short length scale, the conductivity model is not
valid.
m. On
such a short length scale, the conductivity model is not
valid.
1 Put another way, on a time scale as short as
the charge relaxation time in a metal, the inertia of the electrons
responsible for the conduction would come into play. (S. Gruber,
``On Charge Relaxation in Good Conductors," Proc. IEEE, Vol.
61 (1973), pp. 237-238.
The inertial force is not included in the conductivity model. In the
opposite extreme, a layer of corn oil about 60,000 miles thick would
be required to make  m exceed
m exceed  e!
e!
Example 15.3.1. Overview of TEM Fields in Open Circuit
Transmission Line Filled with Lossy Material (continued)
In Sec. 14.8, we considered the nature of the electromagnetic
fields in a conductor sandwiched between ``perfectly conducting"
plates. Example 14.8.2 was devoted to an overview of electromagnetic
regimes pictured in the length-time plane, Fig. 14.8.3, redrawn as Fig.
15.3.3. As the frequency was raised in that
example with l \gg l*, the line 
 m = 1
indicated that quasi-stationary conduction had given way to magnetic
diffusion (the resistor had become a system of distributed resistors
and inductors). In that specific example, this was the line at which
the long wave approximation broke down,
m = 1
indicated that quasi-stationary conduction had given way to magnetic
diffusion (the resistor had become a system of distributed resistors
and inductors). In that specific example, this was the line at which
the long wave approximation broke down,  l \approx 1. With l
\ll l*, we have seen that as the frequency was raised, the crossing
of the line
l \approx 1. With l
\ll l*, we have seen that as the frequency was raised, the crossing
of the line 
 e = 1 denoted that a resistor had changed into
a system of distributed resistors in parallel with distributed
capacitors.
e = 1 denoted that a resistor had changed into
a system of distributed resistors in parallel with distributed
capacitors.
This example has a misleading simplicity that can be traced to the
fact that it actually possesses more than one length scale and
conductivity. To impose the TEM fields by means of the source, it was
necessary to envision the slab of conductor as making perfect
electrical contact with perfectly conducting plates. In reality,
the boundary condition used to represent these plates implies
conditions on still other parameters, notably the electrical
properties and thickness of the plates.
As the frequency is raised for a system in the upper half-plane
(l larger than the matching length), why do we not see a
transition to electromagnetic waves at 
 em = 1 rather
than
em = 1 rather
than 
 e = 1? The perfectly conducting plates force the
displacement current to compete with the conduction current on its
``own" length scale (either the skin depth or the electromagnetic
wavelength). Thus, in this example, we do not make a transition from
magnetic diffusion (with a penetration length determined by the skin
depth
e = 1? The perfectly conducting plates force the
displacement current to compete with the conduction current on its
``own" length scale (either the skin depth or the electromagnetic
wavelength). Thus, in this example, we do not make a transition from
magnetic diffusion (with a penetration length determined by the skin
depth 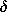 ) to a damped electromagnetic wave (with a decay
length of twice l*) until the electromagnetic wavelength
) to a damped electromagnetic wave (with a decay
length of twice l*) until the electromagnetic wavelength 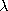 = 2
= 2 /
/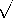
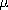

 has become as short as the
skin depth. Both are decreasing with increasing frequency. However,
the skin depth (which decreases as 1/
has become as short as the
skin depth. Both are decreasing with increasing frequency. However,
the skin depth (which decreases as 1/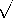
 ) is equal to the
wavelength (which decreases as 1/
) is equal to the
wavelength (which decreases as 1/ ) only as the frequency
reaches
) only as the frequency
reaches 
 e = 2
e = 2 2 (for present purposes,
``
2 (for present purposes,
``
 e = 1").
e = 1").
In the lower half-plane, where systems are smaller than the
characteristic length, why was the transition at 
 e = 1
evident in the surface current density in the plates but not
in the spatial distribution of the fields? The electric
field was found to remain uniform until the frequency had been raised to
e = 1
evident in the surface current density in the plates but not
in the spatial distribution of the fields? The electric
field was found to remain uniform until the frequency had been raised to

 em = 1. Here again, the ``perfectly conducting"
plates obscure the general situation. The conducting block has
uniform conductivity. As a result, it can support no volume charge
density, regardless of the frequency. In the EQS limit, it is
the charge density that shapes the electric field distribution.
Here the only charges are at
the interfaces between the block and the perfectly conducting
plates. Until magnetic induction comes into play at
em = 1. Here again, the ``perfectly conducting"
plates obscure the general situation. The conducting block has
uniform conductivity. As a result, it can support no volume charge
density, regardless of the frequency. In the EQS limit, it is
the charge density that shapes the electric field distribution.
Here the only charges are at
the interfaces between the block and the perfectly conducting
plates. Until magnetic induction comes into play at 
 em
= 1, these surface charges assume whatever distribution they must to
be consistent with an irrotational electric field. As a result, the
plates make the EQS fields essentially uniform, and the appropriate
model simplifies to one lumped parameter C in parallel with one
lumped parameter R.
em
= 1, these surface charges assume whatever distribution they must to
be consistent with an irrotational electric field. As a result, the
plates make the EQS fields essentially uniform, and the appropriate
model simplifies to one lumped parameter C in parallel with one
lumped parameter R.
15.4 Energy, Power, and Force
Maxwell's equations attribute an excitation (E and H) to
every point in space. Consistent with this view, energy density and
power flow density must be associated with every point in space as
well. Poynting's theorem, Sec. 11.2, does that. Poynting's theorem
identifies energy storage and dissipation associated with the
polarization and magnetization processes.
Each self-consistent macroscopic set of equations must possess an
energy conservation principle, maybe including terms describing
transformation of energy into other forms, like heat, if dissipation
is present. An example was given in Sec. 11.3 of a conservation
principle for the approximate description of EQS fields with a
density of power flow vector that was different from E x
H. This alternate form of an energy conservation principle was
better suited to the EQS description, because it did not contain the
H field which is not usually evaluated in the EQS approximation.
Instead, the charge conservation law (derived from Ampère's law)
was used to find the currents flowing in the system.
An important application of the concept of energy was the derivation
of the force on macroscopic material. The force on a dielectric or
magnetic object computed from energy change can include correctly the
contributions to the net force from fringing fields even though the
field expressions neglect them, if the energy associated with the
fringing field does not change in a small displacement of the object.
Energy and Quasistatics
Because magnetic and electric
energy storages, respectively, are negligible in EQS and MQS systems, a
comparison of energy densities can also be used to establish the
validity of a quasistatic approximation. Specifically, we will see
that in systems characterized by one length scale, the ratio of
magnetic to electric energy storage takes the form
 where l* is the characteristic length
where l* is the characteristic length
 familiar from Secs. 14.8
\footnote2In Sec. 14.8, twice
this length was found to be the decay length for an electromagnetic
wave. and 15.3 and K is of the order of unity.
familiar from Secs. 14.8
\footnote2In Sec. 14.8, twice
this length was found to be the decay length for an electromagnetic
wave. and 15.3 and K is of the order of unity.
Energy arguments can also be the basis for simple models that
modestly extend the frequency range of quasi-stationary conduction.
A second object in this section is the illustration of how these
models are deduced.
As the frequency is raised, one of two processes leads to a
modification in the field sources, and hence of the fields. If
l is less than l*, so that 1/ e is the first
reciprocal characteristic time encountered as
e is the first
reciprocal characteristic time encountered as  is raised, then
the current density is progressively altered to supply unpaired
charge to regions of nonuniform
is raised, then
the current density is progressively altered to supply unpaired
charge to regions of nonuniform  and
and  . Alternatively, if
l is larger than l*, so that 1/
. Alternatively, if
l is larger than l*, so that 1/ m is the shortest
reciprocal characteristic time, magnetic induction alters the current
density notonly in its magnitude and time dependence but in its spatial
distribution as well.
Fully dynamic fields, in which all three (or more) characteristic
times are of the same order of magnitude are difficult to analyze
because the distribution of sources is not known until the fields
have been solved selfconsistently, often a difficult task. However,
if the frequency is lower than the lowest reciprocal time, the field
distributions still approximate those for stationary conduction.
This makes it possible to approximate the energy storages, and hence
to identify both the conditions for the system to be EQS or MQS and
to develop models that are appropriate for frequencies approaching
the lowest reciprocal characteristic time.
m is the shortest
reciprocal characteristic time, magnetic induction alters the current
density notonly in its magnitude and time dependence but in its spatial
distribution as well.
Fully dynamic fields, in which all three (or more) characteristic
times are of the same order of magnitude are difficult to analyze
because the distribution of sources is not known until the fields
have been solved selfconsistently, often a difficult task. However,
if the frequency is lower than the lowest reciprocal time, the field
distributions still approximate those for stationary conduction.
This makes it possible to approximate the energy storages, and hence
to identify both the conditions for the system to be EQS or MQS and
to develop models that are appropriate for frequencies approaching
the lowest reciprocal characteristic time.
The first step in this process is to determine the
quasi-stationary fields. The second is to use these fields to evaluate
the total electric and magnetic energy storages as well as the total
energy dissipation.
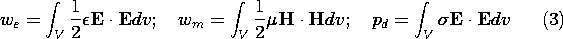 If it is found that the ratio of magnetic to electric energy storage
takes the form of (1), and that if l is either very small or very
large compared to the characteristic length, then we can presumably
model the system by either the R-C or the L-R circuit of Fig. 15.4.1.
If it is found that the ratio of magnetic to electric energy storage
takes the form of (1), and that if l is either very small or very
large compared to the characteristic length, then we can presumably
model the system by either the R-C or the L-R circuit of Fig. 15.4.1.
 As the third step, parameters in these circuits are determined by
comparing we , wm, and pd, as found from the QSC fields using
(3), to these quantities determined in terms of the circuit
variables.
As the third step, parameters in these circuits are determined by
comparing we , wm, and pd, as found from the QSC fields using
(3), to these quantities determined in terms of the circuit
variables.
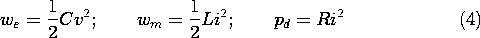 In general, the circuit models are valid only up to frequencies
approaching, but not equal to, the lowest reciprocal time for the
system. In the following example, we will find that the R-C circuit is
an exact model for the EQS system, so that the model is valid even for
frequencies beyond 1/
In general, the circuit models are valid only up to frequencies
approaching, but not equal to, the lowest reciprocal time for the
system. In the following example, we will find that the R-C circuit is
an exact model for the EQS system, so that the model is valid even for
frequencies beyond 1/ e. However, because the fields can be
strongly altered by rate processes if the frequency is equal to the
lowest reciprocal time, it is generally not appropriate to use the
equivalent circuits except to take into account energy storage effects
coming into play as the frequency approaches 1/RC or R/L.
e. However, because the fields can be
strongly altered by rate processes if the frequency is equal to the
lowest reciprocal time, it is generally not appropriate to use the
equivalent circuits except to take into account energy storage effects
coming into play as the frequency approaches 1/RC or R/L.
Example 15.4.1. Energy Method for Deriving an Equivalent Circuit
The block of uniformly conducting material sandwiched between
plane parallel perfectly conducting plates, as shown in Fig. 14.8.1, was
the theme of Sec. 14.8. This gives the opportunity to see how the
low-frequency model developed here fits into the general picture provided
by that section.
In the conducting block, the quasi-stationary conduction (QSC)
fields have the distributions
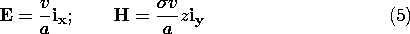 The total electric and magnetic energies and total dissipation
follow from an integration of the respective densities over the volume
of the system in accordance with (3)
The total electric and magnetic energies and total dissipation
follow from an integration of the respective densities over the volume
of the system in accordance with (3)
 where v and i are the terminal voltage and current.
where v and i are the terminal voltage and current.
Comparison of (4) and (6) shows that
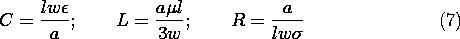 Because the entire volume of the system considered here has
uniform properties, there are no sources of the electric field (charge
densities) in the volume of the system. As a result, the capacitance
C found here is no different than if the volume were filled with a
perfectly insulating material. By contrast, if the slab were of
nonuniform conductivity, as in Example 7.2.1, the capacitance, and
hence equivalent circuit, found by this energy method would not be so
``obvious."
The inductance of the equivalent circuit does reflect a
distribution of the source of the magnetic field, for the current
density is distributed throughout the volume of the slab.
By using the energy argument, we have acknowledged that there is a
distribution of current paths, each having a different flux linkage.
Strictly, when the flux linked by any current path is the same,
inductance is only defined for perfectly conducting current
paths.
Because the entire volume of the system considered here has
uniform properties, there are no sources of the electric field (charge
densities) in the volume of the system. As a result, the capacitance
C found here is no different than if the volume were filled with a
perfectly insulating material. By contrast, if the slab were of
nonuniform conductivity, as in Example 7.2.1, the capacitance, and
hence equivalent circuit, found by this energy method would not be so
``obvious."
The inductance of the equivalent circuit does reflect a
distribution of the source of the magnetic field, for the current
density is distributed throughout the volume of the slab.
By using the energy argument, we have acknowledged that there is a
distribution of current paths, each having a different flux linkage.
Strictly, when the flux linked by any current path is the same,
inductance is only defined for perfectly conducting current
paths.
Which equivalent circuit is appropriate? Here we decide by
comparing the stored energies.
 Thus, as we anticipated with (1), the system can be EQS if l \ll
l* and MQS if l \gg l*. The appropriate equivalent
circuit in Fig. 15.4.1 is the R-C circuit if l \ll l* and is the
L-R circuit if l \gg l*.
Thus, as we anticipated with (1), the system can be EQS if l \ll
l* and MQS if l \gg l*. The appropriate equivalent
circuit in Fig. 15.4.1 is the R-C circuit if l \ll l* and is the
L-R circuit if l \gg l*.
The simple circuits of Fig. 15.4.1 are
not generally valid if the frequency reaches the reciprocal of the
longest characteristic time, since the field distributions have
changed by then. In terms of the circuit elements, this
means that in order for the circuits to be equivalent to the physical
system, the time rates of change must remain slow enough so that
 RC < 1 or
RC < 1 or  L/R < 1.
L/R < 1.
P R O B L E M S |
|---|
| | \problem1
|
|---|
A theme from Chap. 5 on has been the use of orthogonal modes to
represent field solutions and satisfy boundary conditions. Make a
table identifying examples and problems illustrating this theme.
| | Macroscopic Media |
|---|
| 15.2.1 | Field lines in the vicinity of a spherical interface between materials
(a) and (b) are shown in Fig. P15.2.1. In each case, describe four
idealized physical situations for which the field lines would be
appropriate.


|
| 15.2.2 | Dipoles at the center of a spherical region and associated fields are
shown in Fig. P15.2.2. In each case, describe four appropriate
idealized physical situations.
|
| | Approximations
|
|---|
| 15.3.1 | In Fig. 15.3.3, a typical length and time are considered the
independent parameters. Suppose that we wish to see the effect of
varying the conductivity with the size held fixed. For example, with
not only the size but the frequency fixed, the material might be
cooling from a very high temperature where it is molten and an ionic
conductor to a low temperature where it is a good insulator.
Using the conductivity rather than the length for the vertical axis,
select a normalization time for the horizontal axis that is
independent of conductivity, and construct a diagram analogous to Fig.
15.3.3. Identify a ``characteristic" conductivity,  *, for
normalizing the conductivity. *, for
normalizing the conductivity.
|
| 15.3.2 | Figure 7.5.3 shows a circular conductor carrying a current that is
returned through a coaxial ``perfectly" conducting ``can." For
sufficiently low frequencies, the electric field and surface charge
densities are as shown in Fig. 7.5.4. The magnetic field is
described in Example 11.3.1 where the effect of the washer-shaped
conductor is neglected.
| \bullet | Third, what time scale  is of interest? is of interest?
|
| (a) | Sketch E and H, as well as the distribution of
 u and Ju. u and Ju.
|
| (b) | Suppose that the length L is on the order of the radius
(a), and (b) is not much smaller than (a). As the frequency is
raised, argue that either charge relaxation will first dominate in
revising the field distribution as in Fig. P15.3.2a, or magnetic
diffusion will dominate as in Fig. P15.3.2b. In the latter case,
describe the current distribution in the conductor by associating it
with an example and a demonstration in this text.
|
| (c) | With L allowed to be large compared to (a), under what
circumstances will the system behave as the lossy transmission line
of Fig. 14.7.1 with G = 0? Discuss the EQS and MQS limits where
this model applies.
|

|
| | Energy, Power, and Force |
|---|
| 15.4.1 | For the system considered in Prob. 15.3.2, use the energy approach to
identify the parameters in the low frequency equivalent circuits of
Fig. 15.4.1, and write the ratio of energies in the form of (1).
Ignore the effect of the washer-shaped conductor.
|
The concept of energy in circuit theory leads directly to the proof
that mutual capacitance terms Cij and mutual inductance terms
Lij are ``reciprocal", Cij = Cji and Lij = Lji.
The Relativity of Perfection
We began the EQS and MQS examples by postulating perfect conductors
whose surfaces form equipotential surfaces in EQS, and which force
n  H = 0 on perfectly conducting surfaces in MQS.
When we studied materials in detail
we learned that ``perfection" is a relative concept. In the
transient excitation of an EQS field, the short term adjustment of
the electric field was such as if the conductors were, in fact,
insulators. In the long term (steady state), surfaces of conductors
became equipotentials. The characteristic time
H = 0 on perfectly conducting surfaces in MQS.
When we studied materials in detail
we learned that ``perfection" is a relative concept. In the
transient excitation of an EQS field, the short term adjustment of
the electric field was such as if the conductors were, in fact,
insulators. In the long term (steady state), surfaces of conductors
became equipotentials. The characteristic time  e defining
long term and short term is a ratio of weighted sums of dielectric
constants divided by a weighted sum of conductivities. The weighting
factors are geometry dependent. Thus one and the same material may
be idealized as an insulator, or a perfect conductor, depending upon
the time rates or frequencies, of the exciting sources.
e defining
long term and short term is a ratio of weighted sums of dielectric
constants divided by a weighted sum of conductivities. The weighting
factors are geometry dependent. Thus one and the same material may
be idealized as an insulator, or a perfect conductor, depending upon
the time rates or frequencies, of the exciting sources.
A similar, albeit not identical, criterion could be set up for
conductors in the presence of magnetic fields. Conductivity times
permeability (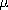
 ) has units of sec/m2 and thus one needs
a multiplier of characteristic length squared to construct a time:
) has units of sec/m2 and thus one needs
a multiplier of characteristic length squared to construct a time:
 m =
m = 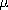
 l2 which determines the behavior of
conductors. When
l2 which determines the behavior of
conductors. When 
 m =
m = 
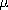
 l2 \gg 1, then
the currents flow only in the ``skin" of the conductor of dimensions
l and the conductor can be idealized as perfect in computing the
field. The losses incurred by the current flow can be computed from
the (approximate) field configuration and added perturbatively to the
energy balance equation. When
l2 \gg 1, then
the currents flow only in the ``skin" of the conductor of dimensions
l and the conductor can be idealized as perfect in computing the
field. The losses incurred by the current flow can be computed from
the (approximate) field configuration and added perturbatively to the
energy balance equation. When 
 m \ll 1, then the currents
have the distribution of ohmic conduction. The current distribution
is determined as for a conduction problem and the quasistatic
H-field is computed from the current distribution using
Ampère's law and Gauss' law.
The product
m \ll 1, then the currents
have the distribution of ohmic conduction. The current distribution
is determined as for a conduction problem and the quasistatic
H-field is computed from the current distribution using
Ampère's law and Gauss' law.
The product  e
e m is of order
m is of order 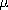
 l2 =
l2 =  2em, does
not contain conductivity, and is the electromagnetic time constant.
When
2em, does
not contain conductivity, and is the electromagnetic time constant.
When 
 em \geq 1 the field is dynamic and the EQS and
MQS assumptions cannot be made. The situation is illustrated
schematically in Fig. 12.7. In Fig. 12.7a, the order is
em \geq 1 the field is dynamic and the EQS and
MQS assumptions cannot be made. The situation is illustrated
schematically in Fig. 12.7. In Fig. 12.7a, the order is  e,
e,
 em and
em and  m with
m with  e \ll
e \ll  em. In this case,
as the frequency is raised, the criterion
em. In this case,
as the frequency is raised, the criterion 
 m = 1 is
passed first. One proceeds from a conduction problem to one of MQS
with H-fields in the presence of perfectly conducting bodies. As
the frequency is raised further the system is electromagnetic in
character. The EQS assumptions never become valid because before one
reaches
m = 1 is
passed first. One proceeds from a conduction problem to one of MQS
with H-fields in the presence of perfectly conducting bodies. As
the frequency is raised further the system is electromagnetic in
character. The EQS assumptions never become valid because before one
reaches 
 e \simeq 1 one has passed the full
electrodynamic description of fields.
e \simeq 1 one has passed the full
electrodynamic description of fields.
 Figure 12.7b shows the case in which the conductors behave as perfect
conductors at low frequencies
Figure 12.7b shows the case in which the conductors behave as perfect
conductors at low frequencies 
 e \ll 1 and become
insulators as
e \ll 1 and become
insulators as 
 e exceeds unity. The EQS approximations
are valid. At still higher frequencies, the electrodynamic laws
prevail. The system cannot behave as a magnetoquasistatic system.
e exceeds unity. The EQS approximations
are valid. At still higher frequencies, the electrodynamic laws
prevail. The system cannot behave as a magnetoquasistatic system.
The last case is one in which,  e,
e,  em and
em and  m are
all comparable, conduction currents, displacement currents and
magnetic flux linkages must be considered all at once. The magnetic
energy storage wm is comparable to the electric energy
storage we and the rate of dissipation is of the order of
m are
all comparable, conduction currents, displacement currents and
magnetic flux linkages must be considered all at once. The magnetic
energy storage wm is comparable to the electric energy
storage we and the rate of dissipation is of the order of
 we and
we and  wm. This case cannot be neatly classified
as either EQS or MQS.
wm. This case cannot be neatly classified
as either EQS or MQS.
Magnetic Charge Model of Magnetization
Magnetization was modeled as the result of orientation of permanent
magnetic dipoles made up of a pair of magnetic charges, positive and
negative. This is not the conventional way of introducing
magnetization. However, the magnetic charge model made possible an
analogy between polarization and magnetization that enabled us to
introduce magnetization into the field equations by analogy to
polarization. More conventional is the approach that treats
magnetization as the result of circulating Ampèrian currents. Of
course, the two approaches lead to the same final result, only the
model is different. To illustrate this, let us rewrite Maxwell's
equations (12.0.1)-(12.0.4) in terms of B, rather than H

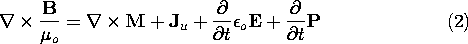

 Thus if B is considered to be the fundamental field variable,
rather than H, then the presence of magnetization manifests
itself by the appearance of the term
Thus if B is considered to be the fundamental field variable,
rather than H, then the presence of magnetization manifests
itself by the appearance of the term 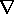 x M next to
Ju in Ampère's law.
x M next to
Ju in Ampère's law. 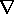 x M is the
Ampèrian current distribution source responsible for driving
B/
x M is the
Ampèrian current distribution source responsible for driving
B/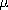 o in the same way as Ju drives it. B is
solenoidal and thus no sources of divergence appear in
Maxwell's equations so reformulated. A ``magnetic dipole" is now
represented by a current flowing around a small loop acting as the
source of B/
o in the same way as Ju drives it. B is
solenoidal and thus no sources of divergence appear in
Maxwell's equations so reformulated. A ``magnetic dipole" is now
represented by a current flowing around a small loop acting as the
source of B/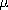 o. This is the model implicit in Tellegen's
claim of the proper description of magnetization, mentioned in Sec.
11.7. Equations (1)-(4) are, of course, identical in content to
(12.0.1)-(12.0.4), because they resulted from the latter by a simple
substitution of B/
o. This is the model implicit in Tellegen's
claim of the proper description of magnetization, mentioned in Sec.
11.7. Equations (1)-(4) are, of course, identical in content to
(12.0.1)-(12.0.4), because they resulted from the latter by a simple
substitution of B/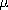 o - M for H. Yet the model of
magnetization was changed by this substitution. As mentioned
earlier, both models lead to the same result even when relativistic
effects are included, but the Ampèrian model calls for greater
care and sophistication, because it contains moving parts (currents)
in the rest frame. This is the other reason that we chose the
magnetic charge model extensively developed by L. J. Chu.
o - M for H. Yet the model of
magnetization was changed by this substitution. As mentioned
earlier, both models lead to the same result even when relativistic
effects are included, but the Ampèrian model calls for greater
care and sophistication, because it contains moving parts (currents)
in the rest frame. This is the other reason that we chose the
magnetic charge model extensively developed by L. J. Chu.
Self-Consistency of Approximate Laws
By dealing with EQS and MQS throughout this subject we concentrated
on phenomena that result from approximate forms of Maxwell's
equations. Terms in the ``exact" equations were ignored and field
configurations were derived from these truncated forms of the
equations. This way of solving problems is not unique to
electromagnetic field theory. Very often it is necessary to ignore
terms in a ``more exact" formulation of a physical problem. When
this is done it is necessary to be fully cognizant of the
consequences of such approximations. One of the examples is the
analysis of carrier flow in semiconductors where one must decide
whether diffusion, conduction by majority or minority carriers and/or
charge neutrality control the carrier flow process. First and
foremost, one must check that the approximations have not introduced
unphysical sources or sinks of energy or particles. This is done by
the development of conservation relations very analogous to the
energy conservation relations used in EQS and MQS that are special
limiting cases of the Poynting theorem obeyed by the full Maxwell
equations.
Next one needs to ascertain whether the problem has been sufficiently
specified by the approximate form of the equations and what boundary
conditions have to be retained, what boundary conditions discarded.
The development of EQS and MQS, with the proof of the uniqueness
theorem provided good examples of the development of a
self-consistent formalism within the framework of a set of
approximate equations.
Mathematical Operators
Maxwell's equations relate the curl and divergence of E and H
to their time rates of change and/or to current and charges. The
curl and divergence are the most important operations on vector
fields and are encountered in any other field dealing with them.
Hydrodynamics is only one of many examples. The student of Maxwell's
equations has the opportunity to learn many facts and identities
relating to vector fields and their operators. Properties of
solenoidal (divergence-free) or conservative (curl-free) fields are
displayed by examples studied.
The Laplacian operator and the gradient operator occur naturally in
the development. Uniqueness of solutions of Laplace's equation
illustrates the adequacy of the field description with appropriately
specified boundary conditions.
Practical Examples
Last but not least, we mention the emphasis of these notes on
examples that provide the student with a ``feel" for the magnitudes
of the effects produced by electric and magnetic fields and with the
reduction to analysis of engineering devices by simplification of
their geometry. This may be called the ``art of modeling". Even
though computer work stations will enable engineers to analyze more
and more complicated geometries, the need for simple models of the
systems analyzed will not decrease. Invention proceeds by means of
simple initial models with the aid of which the design of the new
device can be sketched out. Detailed analysis does not precede, but
follows the initial design.
The examples treated in the notes naturally fell into those
illlustrating EQS and MQS. The electret microphone was one such
example in EQS. It introduced the technique of linearization, the
mathematical formulation of the physical requirement that the
microphone faithfully reproduce the time dependence of the pressure
excited on the microphone membrane. Nonlinear behavior of the
microphone leads to distortion. The charging of a conducting sphere
in an ionized gas was an example illustrating the operation of
electrostatic precipitators. The capacitive attenuator not only
served as the vehicle for the development of the modal expansion, but
also demonstrated the principle of the design of attenuators with a
scale linear in db. We learned the principles behind an
electrocardiogram and ascertained the safety of handling of ``live"
high voltage transmission lines. We found that the currents induced
in the human body under these conditions are much below the level of
biological currents of the human body. The principle of operation of
a Traveling Wave Tube was the legitimate purvue of EQS, because the
wavelength \Lambda of a bunched beam moving at a tenth of the speed
of light is much smaller than the free-space wavelength, and thus the
criterion  2
2 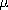 o
o o\Lambda2 \ll 1 is fully met on the
scale of \Lambda comparable to the spatial variation of the
electric field.
The MQS examples dealt with the reading and recording of magnetic
tapes, electric generators and relays. The fact that the fields
surrounding a magnetic tape obey Laplace's equation and thus decay
exponentially with distance away from the tape illustrated the need
for careful design of the recording and reading head. The expression
of torque as the rate of change of energy with angle emphasized the
requirement for the creation of large energy storage. It is no
coincidence that EQS motors are academic curiosities and not of
practical use. This is the consequence of the asymmetry of nature in
not providing us with a copious supply of magnetic monopoles, but
affording a practically limitless one of electric monopoles (electrons,
protons, ions, holes in semiconductors). This enables us to produce
much larger magnetic energy densities
o\Lambda2 \ll 1 is fully met on the
scale of \Lambda comparable to the spatial variation of the
electric field.
The MQS examples dealt with the reading and recording of magnetic
tapes, electric generators and relays. The fact that the fields
surrounding a magnetic tape obey Laplace's equation and thus decay
exponentially with distance away from the tape illustrated the need
for careful design of the recording and reading head. The expression
of torque as the rate of change of energy with angle emphasized the
requirement for the creation of large energy storage. It is no
coincidence that EQS motors are academic curiosities and not of
practical use. This is the consequence of the asymmetry of nature in
not providing us with a copious supply of magnetic monopoles, but
affording a practically limitless one of electric monopoles (electrons,
protons, ions, holes in semiconductors). This enables us to produce
much larger magnetic energy densities  H2 than electric
energy densities
H2 than electric
energy densities  E2, because the
magnetic fields do not encounter breakdown in the same way as
electric fields. Breakdown is caused by the acceleration of
monopoles experiencing the forces qm H or qE
respectively, which then produce by impact ionization further charges
in an avalanche process. A static magnetic field does not experience
breakdown because there are no macroscopic quantities of magnetic
monopoles around. Of course, in addition, the operation of magnetic
motors depends on the existence of good conductors and ferromagnetic
materials in order to produce sources of magnetic fields efficiently.
The recent demonstration of high temperature superconductivity is
likely to revolutionize the design of motors, generators, and
transformers, if fabrication of superconducting wires from these
materials can be successfully demonstrated.
E2, because the
magnetic fields do not encounter breakdown in the same way as
electric fields. Breakdown is caused by the acceleration of
monopoles experiencing the forces qm H or qE
respectively, which then produce by impact ionization further charges
in an avalanche process. A static magnetic field does not experience
breakdown because there are no macroscopic quantities of magnetic
monopoles around. Of course, in addition, the operation of magnetic
motors depends on the existence of good conductors and ferromagnetic
materials in order to produce sources of magnetic fields efficiently.
The recent demonstration of high temperature superconductivity is
likely to revolutionize the design of motors, generators, and
transformers, if fabrication of superconducting wires from these
materials can be successfully demonstrated.
\bye
The sphere has simple field solutions only in the quasistatic limit.
This does not mean, however, that the only simple examples involving
spheres must be confined to quasistatics. In the study of Rayleigh
scattering, we considered a sphere polarized by a uniform electric
field, the field of a parallel plane wave of wavelength much larger
than the radius of the sphere. The polarization current thus
produced acted as an antenna and radiated as a consequence, i.e.
scattered some of the incident field. Thus, the EQS solutions in the
near field connected to the full radiation field of a small dipole.
The only restriction was that the radius of the sphere be small
compared with a wavelength.
--more chapter 15
The EQS and MQS solutions turned out to be special cases of the TM
and TE modes of parallel plate waveguides solved by the full
Maxwell's equations with no approximations. They are cutoff in the
quasistatic approximation, but turn into propagating modes if the
frequency is raised above the cutoff frequency. This transition from
cutoff to propagation is a particulary vivid illustration of the
transition from quasistatics to electrodynamics.
%%%%%%%%%%%%%%%%%%%%%%old 15%%%%%%%%%%%%%%%%%%%
15.5 Energy and Quasistatics
If  is somewhat less than the reciprocal of the longest
characteristic time (either 1/
is somewhat less than the reciprocal of the longest
characteristic time (either 1/ e or 1/
e or 1/ m in Fig. 15.2.1),
the system is in a state of essentially steady conduction.
Because the fields are in fact time-varying, this state is termed one
of quasistationary conduction (QSC). Such systems were the subject of
the first half of Chap. 7.
m in Fig. 15.2.1),
the system is in a state of essentially steady conduction.
Because the fields are in fact time-varying, this state is termed one
of quasistationary conduction (QSC). Such systems were the subject of
the first half of Chap. 7.
-here
In this section, we return to the distinction between EQS and MQS
systems introduced in Sec. 11.2. There we observed that in the EQS
and MQS approximations, the magnetic and electric energy storages were
respectively neglected. Here, we will reverse the reasoning. A
comparison of the electric and magnetic energy storages will be used
to show how the approximation depends on the length scale and the
properties of the system.
\bye
%%%%%%%%%%%%%%%%%%%not used in final revision%%%%%%%%%%%%
In the EQS range of Fig. 15.3.2a, 
 e is
arbitrary, so the terms on the right in Ampère's law (the conduction
and displacement current densities) can be of the same order. This
same law then implies that \unH \approx
e is
arbitrary, so the terms on the right in Ampère's law (the conduction
and displacement current densities) can be of the same order. This
same law then implies that \unH \approx 
 em\unE,
from which it follows that the right-hand side of Faraday's law, (8), is
of the order of (
em\unE,
from which it follows that the right-hand side of Faraday's law, (8), is
of the order of (
 em)2E. Because
em)2E. Because 
 em \ll
1, it follows that the right-hand side of (8) is negligible compared
to the left (the magnetic induction can be ignored in Faraday's law).
Thus, the electric field is essentially irrotational and (6)
and (8) become the primary EQS field laws (7.0.1) and (7.0.2).
In EQS systems, it is the divergence of Ampère's law that is of
primary interest, yielding the charge conservation equation (7.0.3).
em \ll
1, it follows that the right-hand side of (8) is negligible compared
to the left (the magnetic induction can be ignored in Faraday's law).
Thus, the electric field is essentially irrotational and (6)
and (8) become the primary EQS field laws (7.0.1) and (7.0.2).
In EQS systems, it is the divergence of Ampère's law that is of
primary interest, yielding the charge conservation equation (7.0.3).
Generally, without having determined the fields, we do not have
the luxury of knowing the electric and magnetic energy storages. For
dynamic fields, the rate processes
3 Processes that
depend on time rates of change. represented by the characteristic
times (and these times multiplied by ratios of lengths) result in a
distribution of the field sources that is generally not known until
after the self-consistent fields have been found.





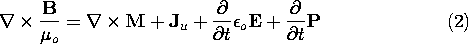


 x M next to
Ju in Ampère's law. Like Ju, the Ampèrian
current density,
x M next to
Ju in Ampère's law. Like Ju, the Ampèrian
current density,  o. Because B is solenoidal, no sources of
divergence appear in Maxwell's equations reformulated in terms of
B. The fundamental source representing magnetization is now a
current flowing around a small loop (magnetic dipole). Equations
(1)-(4) are, of course, identical in content to
(12.0.1)-(12.0.4) because they resulted from the latter by a simple
substitution of B/
o. Because B is solenoidal, no sources of
divergence appear in Maxwell's equations reformulated in terms of
B. The fundamental source representing magnetization is now a
current flowing around a small loop (magnetic dipole). Equations
(1)-(4) are, of course, identical in content to
(12.0.1)-(12.0.4) because they resulted from the latter by a simple
substitution of B/
 ,
,  , and
, and  . In common engineering practice, frequencies
range from 10-2 Hz used to characterize insulation to optical
frequencies in the range of 1015 Hz. Again, nature provides
frequencies that range even more widely, including the reciprocal of
millions of years for terrestrial magnetic fields in one extreme and
the frequencies of gamma rays in the other.
. In common engineering practice, frequencies
range from 10-2 Hz used to characterize insulation to optical
frequencies in the range of 1015 Hz. Again, nature provides
frequencies that range even more widely, including the reciprocal of
millions of years for terrestrial magnetic fields in one extreme and
the frequencies of gamma rays in the other.


 e and the magnetic diffusion time
e and the magnetic diffusion time 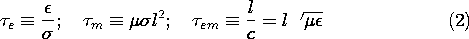


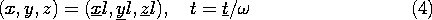
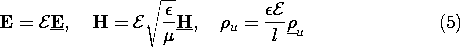

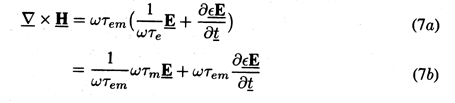
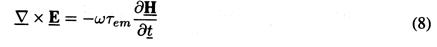




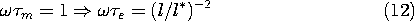
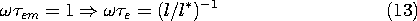


 l \approx 1. With l
\ll l*, we have seen that as the frequency was raised, the crossing
of the line
l \approx 1. With l
\ll l*, we have seen that as the frequency was raised, the crossing
of the line  ) to a damped electromagnetic wave (with a decay
length of twice l*) until the electromagnetic wavelength
) to a damped electromagnetic wave (with a decay
length of twice l*) until the electromagnetic wavelength  = 2
= 2 /
/


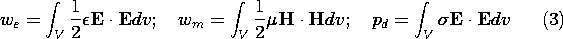

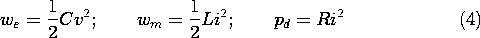
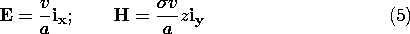

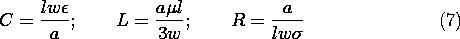



 u and Ju.
u and Ju.

 H = 0 on perfectly conducting surfaces in MQS.
When we studied materials in detail
we learned that ``perfection" is a relative concept. In the
transient excitation of an EQS field, the short term adjustment of
the electric field was such as if the conductors were, in fact,
insulators. In the long term (steady state), surfaces of conductors
became equipotentials. The characteristic time
H = 0 on perfectly conducting surfaces in MQS.
When we studied materials in detail
we learned that ``perfection" is a relative concept. In the
transient excitation of an EQS field, the short term adjustment of
the electric field was such as if the conductors were, in fact,
insulators. In the long term (steady state), surfaces of conductors
became equipotentials. The characteristic time