Maxwell's integral laws encompass the laws of electrical circuits. The transition from fields to circuits is made by associating the relevant volumes, surfaces, and contours with electrodes, wires, and terminal pairs. Begun in an informal way in Chap. 1, this use of the integral laws will be formalized and examined as the following chapters unfold. Indeed, many of the empirical origins of the integral laws are in experiments involving electrodes, wires and the like.
The remarkable fact is that the integral laws apply to any combination of volume and enclosing surface or surface and enclosing contour, whether associated with a circuit or not. This was implicit in our use of the integral laws for deducing field distributions in Chap. l.
Even though the integral laws can be used to determine the fields in highly symmetric configurations, they are not generally applicable to the analysis of realistic problems. Reasons for this lie beyond the geometric complexity of practical systems. Source distributions are not generally known, even when materials are idealized as insulators and "perfect" conductors. In actual materials, for example, those having finite conductivity, the self-consistent interplay of fields and sources, must be described.
Because they apply to arbitrary volumes, surfaces, and contours, the integral laws also contain the differential laws that apply at each point in space. The differential laws derived in this chapter provide a more broadly applicable basis for predicting fields. As might be expected, the point relations must involve information about the shape of the fields in the neighborhood of the point. Thus it is that the integral laws are converted to point relations by introducing partial derivatives of the fields with respect to the spatial coordinates.
The plan in this chapter is first to write each of the integral laws in terms of one type of integral. For example, in the case of Gauss' law, the surface integral is converted to one over the volume V enclosed by the surface.
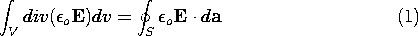
Here div is some combination of spatial derivatives of  o E
to be determined in the next section. With this mathematical theorem
accepted for now, Gauss' integral law, (1.3.1), can be written in
terms of volume integrals.
o E
to be determined in the next section. With this mathematical theorem
accepted for now, Gauss' integral law, (1.3.1), can be written in
terms of volume integrals.
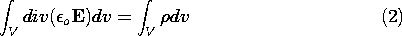
The desired differential form of Gauss' law is obtained by equating the integrands in this expression.

Is it true that if two integrals are equal, their integrands are as well? In general, the answer is no! For example, if x2 is integrated from 0 to 1, the result is the same as for an integration of 2x/3 over the same interval. However, x2 is hardly equal to 2x/3 for every value of x.
It is because the volume V is arbitrary that we can equate the integrands in (1). For a one-dimensional integral, this is equivalent to having endpoints that are arbitrary. With the volume arbitrary (the endpoints arbitrary), the integrals can only be equal if the integrands are as well.
The equality of the three-dimensional volume integration on the left in (1) and the two-dimensional surface integration on the right is analogous to the case of a one-dimensional integral being equal to the function evaluated at the integration endpoints. That is, suppose that the operator der operates on f(x) in such a way that
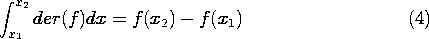
The integration on the left over the "volume" interval between x1 and x2 is reduced by this "theorem" to an evaluation on the "surface," where x = x1 and x = x2.
The procedure for determining the operator der in (4) is
analogous to that used to deduce the divergence and curl operators in
Secs. 2.1 and 2.4, respectively. The point x at which der is to be
evaluated is taken midway in the integration interval, as in
Fig. 2.0.1. Then the interval is taken as incremental ( x =
x2 - x1) and for small
x =
x2 - x1) and for small 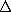 x, (4) becomes
x, (4) becomes
\fig2.0.12inGeneral function of x defined between endpoints x1 and x2.
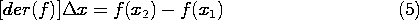
It follows that
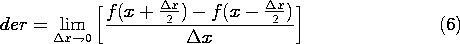
Thus, as we knew to begin with, der is the derivative of f with respect to x.
Byproducts of the derivation of the divergence and curl operators in Secs. 2.1 and 2.4 are the integral theorems of Gauss and Stokes, derived in Secs. 2.2 and 2.5, respectively. A theorem is a mathematical relation and must be distinguished from a physical law, which establishes a physical relation among physical variables. The differential laws, together with the operators and theorems that are the point of this chapter, are summarized in Sec. 2.8.

