If Gauss' integral theorem, (1.3.1), is to be written with the surface integral replaced by a volume integral, then it is necessary that an operator be found such that
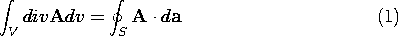
With the objective of finding this divergence operator, div, (1) is applied to an incremental volume
V. Because the volume is small, the volume integral on the left can be taken as the product of the integrand and the volume. Thus, the divergence of a vector A is defined in terms of the limit of a surface integral.
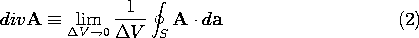
Once evaluated, it is a function of r. That is, in the limit, the volume shrinks to zero in such a way that all points on the surface approach the point r. With this condition satisfied, the actual shape of the volume element is arbitrary.
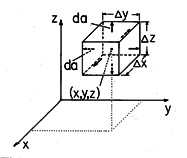
In Cartesian coordinates, a convenient incremental volume is a rectangular parallelepiped
0 in view, the right-hand side of (2) is approximated by
Figure 2.1.1. Incremental volume element for determination of divergence operator.
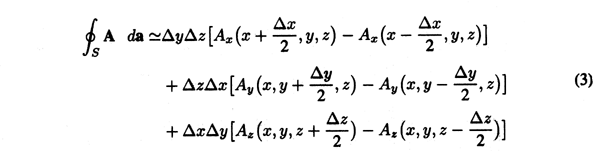
With the above expression used to evaluate (2), along with
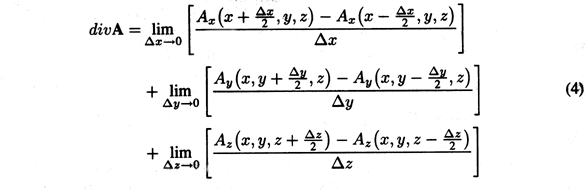
It follows that in Cartesian coordinates, the divergence operator is
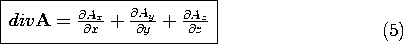
This result suggests an alternative notation. The del operator is defined as
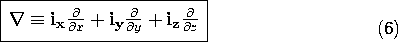
so that (5) can be written as
The div notation suggests that this combination of derivatives describes the outflow of A from the neighborhood of the point of evaluation. The definition (2) is independent of the choice of a coordinate system. On the other hand, the del notation suggests the mechanics of the operation in Cartesian coordinates. We will have it both ways by using the del notation in writing equations in Cartesian coordinates, but using the name divergence in the text.
Problems 2.1.4 and 2.1.6 lead to the divergence operator in cylindrical and spherical coordinates, respectively (summarized in Table I at the end of the text), and provide the opportunity to develop the connection between the general definition, (2), and specific representations.
