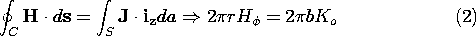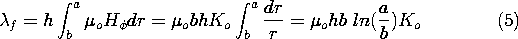3.4
Quasistatic Systems

Whether we ignore the magnetic induction and use the EQS

approximation, or neglect the displacement current and make a MQS approximation, times of interest must be long compared to the time _em required for an electromagnetic wave to propagate at the velocity c over the largest length L of the system.

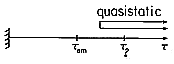
This requirement is given a graphic representation in Fig. 3.4.1.

Figure 3.4.1 Range of characteristic times over which quasistatic approximation is valid. The transit time of an electromagnetic wave is _em while _? is a time characterizing the dynamics of the quasistatic system.

For a given characteristic time (for example, a given reciprocal frequency), it is clear from (1) that the region described by the quasistatic laws is limited in size. Systems can often be divided into subregions that are small enough to be quasistatic but, by virtue of being interconnected through their boundaries, are dynamic in their behavior. With the elements regarded as the subregions, electric circuits are an example. In the physical world of perfect conductors and free space (to which we are presently limited), it is the topology of the conductors that determines whether these subregions are EQS or MQS.

A system that is described by quasistatic laws but retains a dynamical behavior exhibits one or more characteristic times. On the characteristic time axis in Fig. 3.4.1, _? is one such time. The quasistatic system model provides a meaningful description provided that the one or more characteristic times _? are long compared to _em. The following example illustrates this concept.

Example 3.4.1. A Quasistatic System Exhibiting Resonance

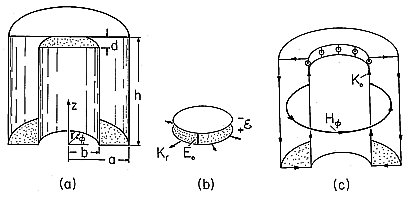
Shown in cross-section in Fig. 3.4.2 is a resonator used in connection with electron beam devices at microwave frequencies. The volume enclosed by its perfectly conducting boundaries can be broken into the two regions shown. The first of these is bounded by a pair of circular plane parallel conductors having spacing d and radius b. This region is EQS and described in Example 3.3.1.

Figure 3.4.2 (a) Quasistatic system showing (b) its EQS subsystem and (c) its MQS subsystem.

The second region is bounded by coaxial, perfectly conducting cylinders which form an annular region having outside radius a and an inside radius b that matches up to the outer edge of the lower plate of the EQS system. The coaxial cylinders are shorted by a perfectly conducting plate at the bottom, where z = 0. A similar plate at the top, where z = h, connects the outer cylinder to the outer edge of the upper plate in the EQS subregion.

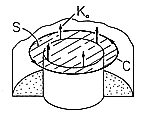
For the moment, the subsystems are isolated from each other by driving the MQS system with a current source K_o (amps/meter) distributed around the periphery of the gap between conductors. This gives rise to axial surface current densities of K_o and -K_o (b/a) on the inner and outer cylindrical conductors and radial surface current densities contributing to J da in the upper and lower plates, respectively. (Note that these satisfy the MQS current continuity requirement.)

Because of the symmetry, the magnetic field can be determined by using the integral MQS form of Ampère's law. So that there is a contribution to the integration of J da, a surface is selected with a normal in the axial direction. This surface is enclosed by a circular contour having the radius r, as shown in Fig. 3.4.3. Because of the axial symmetry, H is independent of , and the integrations on S and C amount to multiplications.

Figure 3.4.3 Surface S and contour C for evaluating H-field using Ampère's law.

Thus, in the annulus,

In the regions outside the annulus, H is zero. Note that this is consistent with Ampère's jump condition, (1.4.16), evaluated on any of the boundaries using the already determined surface current densities. Also, we will find in Chap. 10 that there can be no time-varying magnetic flux density normal to a perfectly conducting boundary. The magnetic field given in (3) satisfies this condition as well.

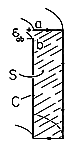
In the hierarchy of MQS laws, we have now satisfied (3.2.5b) and (3.2.6b) and come next to Faraday's law, (3.2.7b). For the present purposes, we are not interested in the details of the distribution of electric field. Rather, we use the integral form of Faraday's law, (1.6.1), integrated on the surface S shown in Fig. 3.4.4. The integral of E ds along the perfect conductor vanishes and we are left with

Figure 3.4.4 Surface S and contour C used to determine EMF using Faraday's law.

where the EMF across the gap is as defined by (1.6.2), and the flux linked by C is consistent with (1.6.8).

These last two expressions combine to give

Just as this expression serves to relate the EMF and surface current density at the gap of the MQS system, (3.3.8) relates the gap variables defined in Fig. 3.4.2b for the EQS subsystem. The subsystems are now interconnected by replacing the distributed current source driving the MQS system with the peripheral surface current density of the EQS system.

In addition, the EMF's of the two subsystems are made to match where they join.

With (3.3.8) and (3.3.6), respectively, substituted for K_r and _ab, these expressions become two differential equations in the two variables E_o and K_o describing the complete system.

Elimination of K_o between these expressions gives

where _o is defined as

and it follows that solutions are a linear combination of sin _o t and cos _o t.

As might have been suspected from the outset, what we have found is a response to initial conditions that is oscillatory, with a natural frequency _o. That is, the parallel plate capacitor that comprises the EQS subsystem, connected in parallel with the one-turn inductor that is the MQS subsystem, responds to initial values of E_o and K_o with an oscillation that at one instant has E_o at its peak magnitude and K_o = 0, and a quarter cycle later has E_o = 0 and K_o at its peak magnitude. Remember that _o E_o is the surface charge density on the lower plate in the EQS section. Thus, the oscillation is between the charges in the EQS subsystem and the currents in the MQS subsystem. The distribution of field sources in the system as a whole is determined by a dynamical interaction between the two subsystems.

If the system were driven by a current source having the frequency , it would display a resonance at the natural frequency _o. Under what conditions can the system be in resonance and still be quasistatic? In this case, the characteristic time for the system dynamics is the reciprocal of the resonance frequency. The EQS subsystem is indeed EQS if b/c \ll , while the annular subsystem is MQS if h/c \ll . Thus, the resonance is correctly described by the quasistatic model if the times have the ordering shown in Fig. 3.4.5. Essentially, this is achieved by making the spacing d in the EQS section very small.

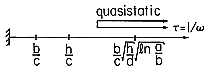
Figure 3.4.5 In terms of characteristic time , the dynamic regime in which the system of Fig. 3.4.2 is quasistatic but capable of being in a state of resonance.

With the region of interest containing media, the appropriate quasistatic limit is often as much determined by the material properties as by the topology. In Chaps. 7 and 10, we will consider lossy materials where the distributions of field sources depend on the time rates of change and a given region can be EQS or MQS depending on the electrical conductivity. We return to the subject of quasistatics in Chaps. 12 and 14.