From a mathematical point of view, the summary of quasistatic laws given in Table 3.6.1 is an outline of the next seven chapters.
An excursion down the left column and then down the right column of the outline represented by Fig. 1.0.1 carries us down the corresponding columns of the table. Gauss' law and the requirement that E be irrotational, (3.2.5a) and (3.2.6a), are the subjects of Chaps. 4-5. In Chaps. 6 and 7, two types of charge density are distinguished and used to represent the effects of macroscopic media on the electric field. In Chap. 6, where polarization charge is used to represent insulating media, charge is automatically conserved. But in Chap. 7, where unpaired charges are created through conduction processes, the charge conservation law, (3.2.7a), comes into play on the same footing as (3.2.5a) and (3.2.6a). In stages, starting in Chap. 4, the ability to predict self-consistent distributions of E and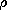
is achieved in this last EQS chapter.
TABLE 3.6.1 SUMMARY OF QUASISTATIC DIFFERENTIAL LAWS IN FREE SPACE
Electroquasistatic Magnetoquasistatic Reference Eq. 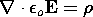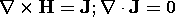(3.2.5) 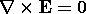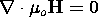(3.2.6) (3.2.7)
Secondary
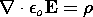(3.2.8) 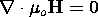(3.2.9)
TABLE 3.6.2 SUMMARY OF QUASISTATIC INTEGRAL LAWS IN FREE SPACE
(1) 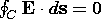(2) 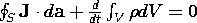(3)
Secondary
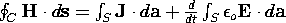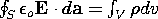(4) (5)
Ampèere's law and magnetic flux continuity, (3.2.5b) and (3.2.6b), are featured in Chap. 8. First, the magnetic field is determined for a given distribution of current density. Because current distributions are often controlled by means of wires, it is easy to think of practical situations where the MQS source, the current density, is known at the outset. But even more, the first half of Chap. 7 was already devoted to determining distributions of "stationary" current densities. The MQS current density is always solenoidal, (3.2.5c), and the magnetic induction on the right in Faraday's law, (3.2.7b), is sometimes negligible so that the electric field can be essentially irrotational. Thus, the first half of Chap. 7 actually starts the sequence of MQS topics. In the second half of Chap. 8, the magnetic field is determined for systems of perfect conductors, where the source distribution is not known until the fields meet certain boundary conditions. The situation is analogous to that for EQS systems in Chap. 5. Chapters 9 and 10 distinguish between effects of magnetization and conduction currents caused by macroscopic media. It is in Chap. 10 that Faraday's law, (3.2.7b), comes into play in a field theoretical sense. Again, in stages, in Chaps. 8-10, we attain the ability to describe a self-consistent field and source evolution, this time of H and its sources, J.
The quasistatic approximations and ordering of laws can just as well be stated in terms of the integral laws. Thus, the differential laws summarized in Table 3.6.1 have the integral law counterparts listed in Table 3.6.2.
