4.9
Summary

The theme in this chapter is set by the two equations that determine E, given the charge density . The first of these, (4.0.1), requires that E be irrotational. Through the representation of E as the negative gradient of the electric potential, , it is effectively integrated.

This gradient operator, determined in Cartesian coordinates in Sec. 4.1 and found in cylindrical and spherical coordinates in the problems of that section, is summarized in Table I. The associated gradient integral theorem, (4.1.16), is added for reference to the integral theorems of Gauss and Stokes in Table II.

The substitution of (1) into Gauss' law, the second of the two laws forming the theme of this chapter, gives Poisson's equation.

The Laplacian operator on the left, defined as the divergence of the gradient of , is summarized in the three standard coordinate systems in Table I.

It follows from the linearity of (2) that the potential for the superposition of charge distributions is the superposition of potentials for the individual charge distributions. The potentials for dipoles and other singular charge distributions are therefore found by superimposing the potentials of point or line charges. The superposition integral formalizes the determination of the potential, given the distribution of charge. With the surface and line charges recognized as special (singular) volume charge densities, the second and third forms of the superposition integral summarized in Table 4.9.1 follow directly from the first. The fourth is convenient if the source and field are two dimensional.

Through Sec. 4.5, the charge density is regarded as given throughout all space. From Sec. 4.6 onward, a shift is made toward finding the field in confined regions of space bounded by surfaces of constant potential. At first, the approach is opportunistic. Given a solution, what problems have been solved? However, the numerical convolution method of Sec. 4.8 is a direct and practical approach to solving boundary value problems with arbitrary geometry.

TABLE 4.9.1 SUPERPOSITION INTEGRALS FOR ELECTRIC POTENTIAL

Volume Charge (4.5.3)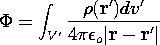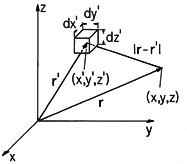
Surface Charge (4.5.5)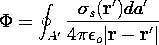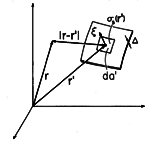
Line Charge (4.5.12)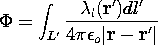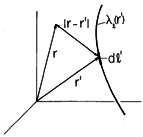
Two-dimensional (4.5.20)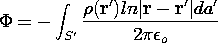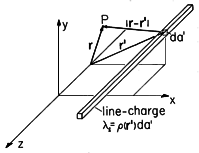
Double-layer (4.5.28)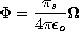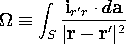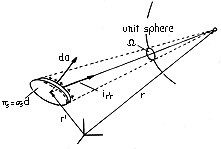