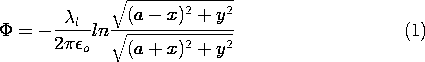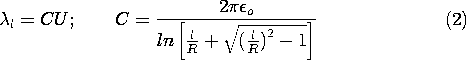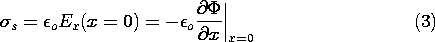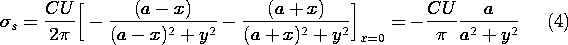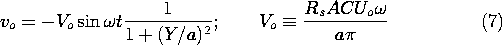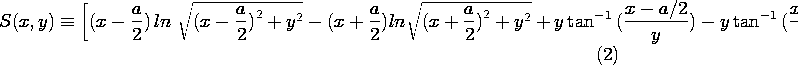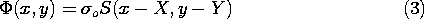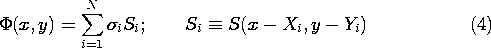4
Electroquasistatic
Fields: The
Superposition Integral
Point of View
4.0 Introduction
The reason for taking up electroquasistatic fields first
is the relative ease with which such a vector field can
be represented. The EQS form of Faraday's law requires that the
electric field intensity E be irrotational.

The electric field intensity is related to the charge density  by Gauss' law.
by Gauss' law.

Thus, the source of an electroquasistatic field is a scalar, the
charge density  . In free space, the source of a
magnetoquasistatic field is a vector, the current density. Scalar
sources, are simpler than vector sources and this is why
electroquasistatic fields are taken up first.
. In free space, the source of a
magnetoquasistatic field is a vector, the current density. Scalar
sources, are simpler than vector sources and this is why
electroquasistatic fields are taken up first.
Most of this chapter is concerned with finding the distribution
of E predicted by these laws, given the distribution of  .
But before the chapter ends, we will be finding fields in limited
regions bounded by conductors. In these more practical situations,
the distribution of charge on the boundary surfaces is not known
until after the fields have been determined. Thus, this chapter sets
the stage for the solving of boundary value problems in Chap. 5.
.
But before the chapter ends, we will be finding fields in limited
regions bounded by conductors. In these more practical situations,
the distribution of charge on the boundary surfaces is not known
until after the fields have been determined. Thus, this chapter sets
the stage for the solving of boundary value problems in Chap. 5.
We start by establishing the electric potential as a scalar
function that uniquely represents an irrotational electric field
intensity. Byproducts of the derivation are the gradient operator and
gradient theorem.
The scalar form of Poisson's equation then results from
combining (1) and (2). This equation will be shown to be linear. It
follows that the field due to a superposition of charges is the
superposition of the fields associated with the individual charge
components. The resulting superposition integral specifies how the
potential, and hence the electric field intensity, can be determined
from the given charge distribution. Thus, by the end of Sec. 4.5, a
general approach to finding solutions to (1) and (2) is achieved.
The art of arranging the charge so that, in a restricted region,
the resulting fields satisfy boundary conditions, is illustrated in
Secs. 4.6 and 4.7. Finally, more general techniques for using the
superposition integral to solve boundary value problems are
illustrated in Sec. 4.8.
For those having a background in circuit theory, it is helpful to
recognize that the approaches used in this and the next chapter are
familiar. The solution of (1) and (2) in three dimensions is like
the solution of circuit equations, except that for the latter, there
is only the one dimension of time. In the field problem, the driving
function is the charge density.
One approach to finding a circuit response is based on first
finding the response to an impulse. Then the response to an
arbitrary drive is determined by superimposing responses to impulses,
the superposition of which represents the drive. This response takes
the form of a superposition integral, the convolution integral.
The impulse response of Poisson's equation that is our starting point
is the field of a point charge. Thus, the theme of this chapter is a
convolution approach to solving (1) and (2).
In the boundary value approach of the next chapter, concepts
familiar from circuit theory are again exploited. There, solutions
will be divided into a particular part, caused by the drive, and a
homogeneous part, required to satisfy boundary conditions. It
will be found that the superposition integral is one way of finding
the particular solution.
4.1 Irrotational Field Represented by Scalar Potential: TheGradient Operator and Gradient Integral Theorem
The integral of an irrotational electric field from some
reference point r\rm ref to the position r is independent
of the integration
path. This follows from an integration of (1) over the surface S
spanning the contour defined by alternative paths I and II, shown in
Fig. 4.1.1. Stokes' theorem, (2.5.4), gives
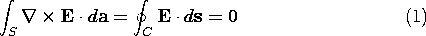

Stokes' theorem employs a contour running around the surface in a
single direction, whereas the line integrals of the electric field
from r to r\rm ref, from point a to point b, run along
the contour in
opposite directions. Taking the directions of the path increments
into account, (1) is equivalent to
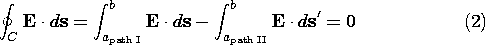
and thus, for an irrotational field, the EMF between two points is
independent of path.
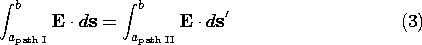
A field that assigns a unique value of the line integral between two
points independent of path of integration is said to be conservative.
With the understanding that the reference point is kept
fixed, the integral is a scalar function of the integration endpoint
r. We use the symbol  (r ) to define this scalar function
(r ) to define this scalar function
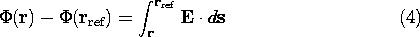
and call  (r) the electric potential of the point r
with respect to the
reference point. With the endpoints consisting of "nodes"
where wires could be attached,
the potential difference of (1) would be the voltage at r
relative to that at the reference. Typically, the latter would be the
"ground" potential. Thus, for an irrotational field, the EMF defined
in Sec. 1.6 becomes the voltage at the point a relative to point b.
(r) the electric potential of the point r
with respect to the
reference point. With the endpoints consisting of "nodes"
where wires could be attached,
the potential difference of (1) would be the voltage at r
relative to that at the reference. Typically, the latter would be the
"ground" potential. Thus, for an irrotational field, the EMF defined
in Sec. 1.6 becomes the voltage at the point a relative to point b.
We shall show that specification of the scalar function  (r)
contains the same information as specification of the field E (r).
This is a remarkable fact because a vector function of r requires, in
general, the specification of three scalar functions of r, say the
three Cartesian components of the vector function. On the other
hand, specification of
(r)
contains the same information as specification of the field E (r).
This is a remarkable fact because a vector function of r requires, in
general, the specification of three scalar functions of r, say the
three Cartesian components of the vector function. On the other
hand, specification of  (r) requires one scalar function of
r.
(r) requires one scalar function of
r.
Note that the expression  (r) = constant represents a surface in
three dimensions. A familiar example of such an expression describes
a spherical surface having radius R.
(r) = constant represents a surface in
three dimensions. A familiar example of such an expression describes
a spherical surface having radius R.

Surfaces of constant potential are called equipotentials.
Shown in Fig. 4.1.2 are the cross-sections of two equipotential
surfaces, one passing through the point r, the other through the point
r +  r. With
r. With  r taken as a differential vector, the
potential at the point r +
r taken as a differential vector, the
potential at the point r +  r differs by the differential
amount
r differs by the differential
amount 
 from that at r. The two equipotential surfaces
cannot intersect. Indeed, if they intersected, both points r and
r +
from that at r. The two equipotential surfaces
cannot intersect. Indeed, if they intersected, both points r and
r +  r would have the same potential, which is contrary to
our assumption.
r would have the same potential, which is contrary to
our assumption.

Illustrated in Fig. 4.1.2 is the shortest distance  n from the
point r to the equipotential at r +
n from the
point r to the equipotential at r +  r. Because of the
differential geometry assumed, the length element
r. Because of the
differential geometry assumed, the length element  n is
perpendicular to both equipotential surfaces. From Fig. 4.1.2,
n is
perpendicular to both equipotential surfaces. From Fig. 4.1.2,  n
= cos
n
= cos 
 r, and we have
r, and we have
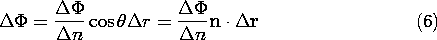
The vector  r in (6) is of arbitrary direction. It is also of
arbitrary differential length. Indeed, if we double the distance
r in (6) is of arbitrary direction. It is also of
arbitrary differential length. Indeed, if we double the distance  n, we double
n, we double 
 and
and  r;
r; 
 /
/ n remains unchanged
and thus (6) holds for any
n remains unchanged
and thus (6) holds for any  r (of differential length). We
conclude that (6) assigns to every differential vector length element
r (of differential length). We
conclude that (6) assigns to every differential vector length element
 r, originating from r, a scalar of magnitude proportional
to the magnitude of
r, originating from r, a scalar of magnitude proportional
to the magnitude of  r and to the cosine of the angle between
r and to the cosine of the angle between
 r and the unit vector n. This assignment of a scalar to a
vector is representable as the scalar product of the vector length
element
r and the unit vector n. This assignment of a scalar to a
vector is representable as the scalar product of the vector length
element  r with a vector of magnitude
r with a vector of magnitude 
 /
/ n and
direction n. That is, (6) is equivalent to
n and
direction n. That is, (6) is equivalent to

where the gradient of the potential is defined as

Because it is independent of any particular coordinate system,
(8) provides the best way to conceptualize the gradient operator.
The same equation provides the algorithm for expressing grad  in any particular coordinate system. Consider, as an example,
Cartesian coordinates. Thus,
in any particular coordinate system. Consider, as an example,
Cartesian coordinates. Thus,
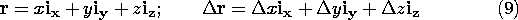
and an alternative to (6) for expressing the differential change in
 is
is
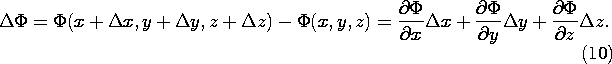
In view of (9), this expression is
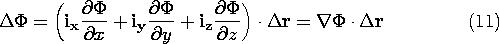
and it follows that in Cartesian coordinates the gradient operation,
as defined by (7), is
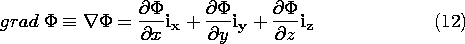
Here, the del operator defined by (2.1.6) is introduced as an
alternative way of writing the gradient operator.
Problems at the end of this chapter serve to illustrate how the
gradient is similarly determined in other coordinates, with results
summarized in Table I at the end of the text.
We are now ready to show that the potential function  (r )
defines E (r ) uniquely. According to (4), the potential
changes from the point r to the point r +
(r )
defines E (r ) uniquely. According to (4), the potential
changes from the point r to the point r +  r by
r by
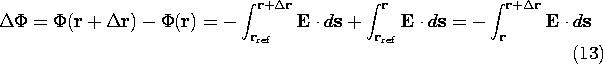
The first two integrals in (13) follow from the definition of  ,
(4). By recognizing that ds is
,
(4). By recognizing that ds is  r and that
r and that  r is of
differential length, so that E (r) can be considered constant
over the length of the vector
r is of
differential length, so that E (r) can be considered constant
over the length of the vector  r, it can be seen that the last
integral in (13) becomes
r, it can be seen that the last
integral in (13) becomes

The vector element  r is arbitrary. Therefore, comparison of
(14) to (7) shows that
r is arbitrary. Therefore, comparison of
(14) to (7) shows that

Given the potential function  (r), the associated electric
field intensity is the negative gradient of
(r), the associated electric
field intensity is the negative gradient of  .
.
Note that we also obtained a useful integral theorem, for if
(15) is substituted into (4), it follows that
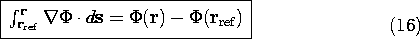
That is, the line integration of the gradient of  is simply the
difference in potential between the endpoints. Of course,
is simply the
difference in potential between the endpoints. Of course,  can be
any scalar function.
can be
any scalar function.
In retrospect, we can observe that the representation of E by
(15) guarantees that it is irrotational, for the vector identity
holds

The curl of the gradient of a scalar potential  vanishes.
Therefore, given an electric field represented by a potential in
accordance with (15), (4.0.1) is automatically satisfied.
vanishes.
Therefore, given an electric field represented by a potential in
accordance with (15), (4.0.1) is automatically satisfied.
Because the preceding discussion shows that the potential  contains full information about the field E, the replacement of
E by grad (
contains full information about the field E, the replacement of
E by grad ( ) constitutes a general solution, or
integral, of (4.0.1).
Integration of a first-order ordinary differential equation leads to
one arbitrary integration constant. Integration of the first-order
vector differential equation curl E = 0 yields a scalar function of
integration,
) constitutes a general solution, or
integral, of (4.0.1).
Integration of a first-order ordinary differential equation leads to
one arbitrary integration constant. Integration of the first-order
vector differential equation curl E = 0 yields a scalar function of
integration,  (r ).
(r ).
Thus far, we have not made any specific assignment for the
reference point r\rm ref. Provided that the potential behaves
properly at
infinity, it is often convenient to let the reference point be at
infinity. There are some exceptional cases for which such a choice is
not possible. All such cases involve problems with infinite amounts
of charge. One such example is the field set up by a charge
distribution that extends to infinity in the \pm z directions, as in
the second Illustration in Sec. 1.3. The field decays like 1/r with
radial distance r from
the charged region. Thus, the line integral of E, (4), from a
finite distance out to infinity involves the difference of ln r
evaluated at the two endpoints and becomes infinite if one endpoint
moves to infinity. In problems that extend to infinity but are not
of this singular nature, we shall assume that the reference is at
infinity.
Example 4.1.1. Equipotential Surfaces
Consider the potential function  (x, y), which is independent
of z:
(x, y), which is independent
of z:

Surfaces of constant potential can be represented by a cross-sectional
view in any x-y plane in which they appear as lines, as shown in
Fig. 4.1.3. For the potential given by (18), the equipotentials appear
in the x-y plane as hyperbolae. The contours passing through the
points (a, a) and (-a, -a) have the potential Vo, while those
at (a, -a) and (-a, a) have potential -Vo.

The magnitude of E is proportional to the spatial rate of
change of  in a direction perpendicular to the constant potential
surface. Thus, if the surfaces of constant potential are sketched at
equal increments in potential, as is done in Fig. 4.1.3, where the
increments are Vo/4, the magnitude of E is inversely
proportional to the spacing between surfaces. The closer the spacing
of potential lines, the higher the field intensity. Field lines,
sketched in Fig. 4.1.3, have arrows that point from high to low
potentials. Note that because they are always perpendicular to the
equipotentials, they naturally are most closely spaced where the field
intensity is largest.
in a direction perpendicular to the constant potential
surface. Thus, if the surfaces of constant potential are sketched at
equal increments in potential, as is done in Fig. 4.1.3, where the
increments are Vo/4, the magnitude of E is inversely
proportional to the spacing between surfaces. The closer the spacing
of potential lines, the higher the field intensity. Field lines,
sketched in Fig. 4.1.3, have arrows that point from high to low
potentials. Note that because they are always perpendicular to the
equipotentials, they naturally are most closely spaced where the field
intensity is largest.
Example 4.1.2. Evaluation of Gradient and Line Integral
Our objective is to exemplify by direct evaluation the fact that
the line integration of an irrotational field between two given points
is independent of the integration path. In particular, consider the
potential given by (18), which, in view of (12), implies the
electric field intensity
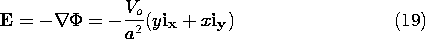
We integrate this vector function along two paths, shown in
Fig. 4.1.3, which join points (1) and (2). For the first path, C1,
y is held fixed at y = a and hence ds = dx ix. Thus,
the integral becomes
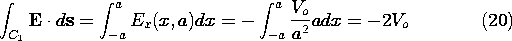
For path C2, y - x2/a = 0 and in general, ds = dx ix + dy
iy, so the required integral is
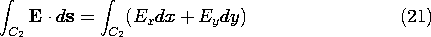
However, for the path C2 we have dy - (2x)dx/a = 0, and hence (21)
becomes
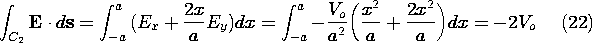
Because E is found by taking the negative gradient of  , and
is therefore irrotational, it is no surprise that (20) and (22) give
the same result.
, and
is therefore irrotational, it is no surprise that (20) and (22) give
the same result.
Example 4.1.3. Potential of Spherical Cloud of Charge
A uniform static charge distribution  o occupies a
spherical region of radius R. The remaining space is charge free
(except, of course, for the balancing charge at infinity). The
following illustrates the determination of a piece-wise continuous
potential function.
o occupies a
spherical region of radius R. The remaining space is charge free
(except, of course, for the balancing charge at infinity). The
following illustrates the determination of a piece-wise continuous
potential function.
The spherical symmetry of the charge distribution imposes a
spherical symmetry on the electric field that makes possible its
determination from Gauss' integral law. Following the approach used
in Example 1.3.1, the field is found to be

The potential is obtained by evaluating the line integral of (4)
with the reference point taken at infinity, r = 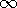 . The
contour follows part of a straight line through the origin. In the
exterior region, integration gives
. The
contour follows part of a straight line through the origin. In the
exterior region, integration gives
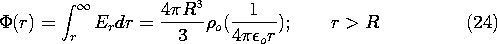
To find  in the interior region, the integration is carried through
the outer region, (which gives (24) evaluated at r = R) and then into
the radius r in the interior region.
in the interior region, the integration is carried through
the outer region, (which gives (24) evaluated at r = R) and then into
the radius r in the interior region.
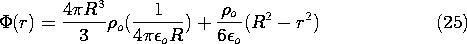
Outside the charge distribution, where r \geq R, the potential acquires the
form of the coulomb potential of a point charge.
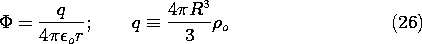
Note that q is the net charge of the distribution.
Visualization of Two-Dimensional Irrotational Fields
In general, equipotentials are three-dimensional surfaces. Thus, any
two-dimensional plot of the contours of constant potential is
the intersection of these surfaces with some given plane. If the
potential is two-dimensional in its dependence, then the equipotential
surfaces have a cylindrical shape. For example, the two-dimensional
potential of (18) has equipotential surfaces that are cylinders
having the hyperbolic cross-sections shown in Fig. 4.1.3.
We review these geometric concepts because we now introduce a
different point of view that is useful in picturing
two-dimensional fields. A three-dimensional picture is now made in
which the third dimension represents the amplitude of the potential
 . Such a picture
is shown in Fig. 4.1.4, where the potential of (18) is used as an
example. The floor of the three-dimensional plot is the x - y
plane, while the vertical dimension is the potential. Thus, contours
of constant potential are represented by lines of constant altitude.
. Such a picture
is shown in Fig. 4.1.4, where the potential of (18) is used as an
example. The floor of the three-dimensional plot is the x - y
plane, while the vertical dimension is the potential. Thus, contours
of constant potential are represented by lines of constant altitude.

The surface of Fig. 4.1.4 can be regarded as a membrane stretched
between supports on the periphery of the region of interest that are
elevated or depressed in proportion to the boundary potential. By the
definition of the gradient, (8), the lines of electric field
intensity follow contours of steepest descent on this surface.
Potential surfaces have their greatest value in the
mind's eye, which pictures a two-dimensional potential as a
contour map and the lines of electric field intensity as the flow
lines of water streaming down the hill.
4.2 Poisson's Equation
Given that E is irrotational, (4.0.1), and given the charge
density in Gauss' law, (4.0.2), what is the distribution of electric
field intensity? It was shown in Sec. 4.1 that we can satisfy the
first of these equations identically by representing the vector E by
the scalar electric potential  .
.

That is, with the introduction of this relation, (4.0.1) has been
integrated.
Having integrated (4.0.1), we now discard it and concentrate
on the second equation of electroquasistatics, Gauss' law.
Introduction of (1) into Gauss' law, (1.0.2), gives
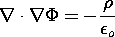
which is identically

Integration of this scalar Poisson's equation, given the charge
density on the right, is the objective in the remainder of this
chapter.
By analogy to the ordinary differential equations of circuit
theory, the charge density on the right is a "driving function."
What is on the left is the operator 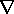 2, denoted by the second
form of (2) and called the Laplacian of
2, denoted by the second
form of (2) and called the Laplacian of  . In Cartesian
coordinates, it follows from the expressions for the divergence and
gradient operators, (2.1.5) and (4.1.12), that
. In Cartesian
coordinates, it follows from the expressions for the divergence and
gradient operators, (2.1.5) and (4.1.12), that
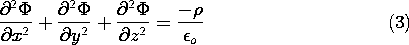
The Laplacian operator in cylindrical and spherical coordinates
is determined in the problems and summarized in Table I at the end of
the text. In Cartesian coordinates, the derivatives in this operator
have constant coefficients. In these other two coordinate systems,
some of the coefficients are space varying.
Note that in (3), time does not appear explicitly as an
independent variable. Hence, the mathematical problem of finding a
quasistatic electric field at the time to for a time-varying charge
distribution  (r , t) is the same as finding the static field
for the time-independent charge distribution
(r , t) is the same as finding the static field
for the time-independent charge distribution  (r ) equal to
(r ) equal to
 (r , t = to), the
charge distribution of the time-varying problem at the particular
instant to.
(r , t = to), the
charge distribution of the time-varying problem at the particular
instant to.
In problems where the charge distribution is given, the
evaluation of a quasistatic field is therefore equivalent to the
evaluation of a succession of static fields, each with a different
charge distribution, at the time of interest. We emphasize this
here to make it understood that the solution of a static electric
field has wider applicability than one would at first suppose: Every
static field solution can represent a "snapshot" at a particular
instant of time. Having said that much, we shall not indicate the
time dependence of the charge density and field explicitly, but shall
do so only when this is required for clarity.
4.3 Superposition Principle
As illustrated in Cartesian coordinates by (4.2.3),
Poisson's equation is a linear second-order differential equation
relating the potential  (r) to the charge distribution
(r) to the charge distribution  (r). By
"linear" we mean that the coefficients of the derivatives in the
differential equation are not functions of the dependent variable
(r). By
"linear" we mean that the coefficients of the derivatives in the
differential equation are not functions of the dependent variable  .
An important consequence of the linearity of Poisson's equation is
that
.
An important consequence of the linearity of Poisson's equation is
that  (r) obeys the superposition principle. It is perhaps
helpful to recognize the analogy to the superposition principle obeyed by
solutions of the linear ordinary differential equations of circuit
theory. Here the principle can be shown as follows.
(r) obeys the superposition principle. It is perhaps
helpful to recognize the analogy to the superposition principle obeyed by
solutions of the linear ordinary differential equations of circuit
theory. Here the principle can be shown as follows.
Consider two different spatial distributions of charge density,
 a(r) and
a(r) and  b(r).
These might be relegated to different regions, or
occupy the same region. Suppose we have found the potentials
b(r).
These might be relegated to different regions, or
occupy the same region. Suppose we have found the potentials
 a and
a and  b which satisfy Poisson's equation, (4.2.3), with the
respective charge distributions
b which satisfy Poisson's equation, (4.2.3), with the
respective charge distributions  a and
a and  b. By definition,
b. By definition,


Adding these expressions, we obtain
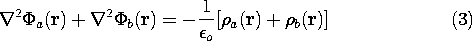
Because the derivatives called for in the Laplacian operation- for
example, the second derivatives of (4.2.3)- give the same result
whether they operate on the potentials and then are summed or
operate on the sum of the potentials, (3) can also be written as
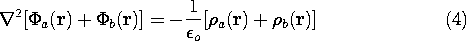
The mathematical statement of the superposition principle follows from
(1) and (2) and (4). That is, if
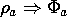

then

The potential distribution produced by the superposition of the
charge distributions is the sum of the potentials associated with the
individual distributions.
4.4 Fields Associated with Charge Singularities
At least three objectives are set in this section. First,
the superposition concept from Sec. 4.3 is exemplified. Second, we
begin to deal with fields that are not highly symmetric. The
potential proves invaluable in picturing such fields, and so we
continue to develop ways of picturing the potential and field
distribution. Finally, the potential functions developed will
reappear many times in the chapters that follow. Solutions to
Poisson's equation as pictured here filling all of space will turn out
to be solutions to Laplace's equation in subregions that are devoid of
charge. Thus, they will be seen from a second point of view in Chap.
5, where Laplace's equation is featured.
First, consider the potential associated with a point charge at
the origin of a spherical coordinate system. The electric field was
obtained using the integral form of Gauss' law in Sec. 1.3, (1.3.12).
It follows from the definition of the potential, (4.1.4), that the
potential of a point charge q is

This "impulse response" for the three-dimensional Poisson's equation
is the starting point in derivations and problem solutions and is
worth remembering.

Consider next the field associated with a positive and a negative
charge, located on the z axis at d/2 and -d/2, respectively. The
configuration is shown in Fig. 4.4.1. In (1), r is the scalar
distance between the point of observation and the charge. With P the
observation position, these distances are denoted in Fig. 4.4.1 by
r+ and r-. It follows from (1) and the superposition principle that
the potential distribution for the two charges is

To find the electric field intensity by taking the negative gradient
of this function, it is necessary to express r+ and r- in
Cartesian coordinates.
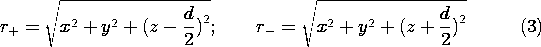
Thus, in these coordinates, the potential for the two charges given by
(2) is
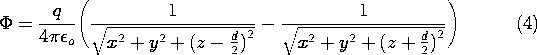
Equation (2) shows that in the immediate vicinity of one or the other
of the charges, the respective charge
dominates the potential. Thus, close to the point charges the
equipotentials are spheres enclosing the charge. Also, this
expression makes it clear that the plane z = 0 is one of zero
potential.
One straightforward way to plot the equipotentials in detail is
to program a calculator to evaluate (4) at a specified coordinate
position. To this end, it is convenient to normalize the potential
and the coordinates such that (4) is
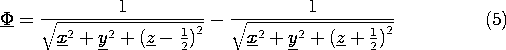
where
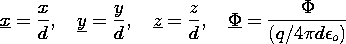
By evaluating  for various coordinate positions, it is possible to
zero in on the coordinates of a given equipotential in an iterative
fashion. The equipotentials shown in Fig. 4.4.2a were plotted in this
way with \un x = 0. Of course, the equipotentials are actually
three-dimensional surfaces obtained by rotating the curves shown
about the z axis.
for various coordinate positions, it is possible to
zero in on the coordinates of a given equipotential in an iterative
fashion. The equipotentials shown in Fig. 4.4.2a were plotted in this
way with \un x = 0. Of course, the equipotentials are actually
three-dimensional surfaces obtained by rotating the curves shown
about the z axis.

Because E is the negative gradient of  , lines of electric field
intensity are perpendicular to the equipotentials. These can
therefore be easily sketched and are shown as lines with arrows in
Fig. 4.4.2a.
, lines of electric field
intensity are perpendicular to the equipotentials. These can
therefore be easily sketched and are shown as lines with arrows in
Fig. 4.4.2a.
Dipole at the Origin
An important limit of (2) corresponds to a view
of the field for an observer far from either of the charges. This is
a very important limit because charge pairs of opposite sign are the
model for polarized atoms or molecules. The dipole is therefore at
center stage in Chap. 6, where we deal with polarizable matter.
Formally, the dipole limit is taken by recognizing that rays joining
the point of observation with the respective charges are essentially
parallel to the r coordinate when r \gg d. The approximate
geometry shown in Fig. 4.4.3 motivates the approximations.
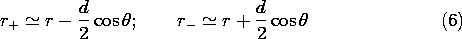

Because the first terms in these expressions are very large compared
to the second, powers of r+ and r- can be expanded in a
binomial expansion.
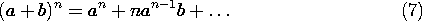
With n = -1, (2) becomes approximately
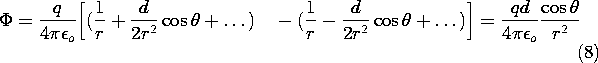
Remember, the potential is pictured in spherical coordinates.
Suppose the equipotential is to be sketched that passes through
the z axis at some specified location. What is the shape of the
potential as we move in the positive 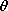 direction? On the left in
(8) is a constant. With an increase in
direction? On the left in
(8) is a constant. With an increase in 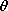 , the cosine function on the
right decreases. Thus, to stay on the surface, the distance r from
the origin must decrease. As the angle approaches
, the cosine function on the
right decreases. Thus, to stay on the surface, the distance r from
the origin must decrease. As the angle approaches  /2, the
cosine decreases to zero, making it clear that the equipotential
must approach the origin. The equipotentials and associated lines of
E are shown in Fig. 4.4.2b.
/2, the
cosine decreases to zero, making it clear that the equipotential
must approach the origin. The equipotentials and associated lines of
E are shown in Fig. 4.4.2b.
The dipole model is made mathematically exact by defining it as
the limit in which two charges of equal magnitude and opposite sign
approach to within an infinitesimal distance of each other while
increasing in magnitude. Thus, with the dipole moment p defined as

the potential for the dipole, (8), becomes

Another more general way of writing (10) with the dipole
positioned at an arbitrary point r' and lying along a
general axis
is to introduce the dipole moment vector. This vector is defined to
be of magnitude p and directed along the axis of the two charges
pointing from the - charge to the + charge. With the unit vector
ir'r defined as being directed from the point
r' (where the dipole is located) to the point of
observation at r, it follows from (10)
that the generalized potential is

\sectnonumPair of Charges at Infinity Having Equal Magnitude and Opposite
Sign
Consider next the appearance of the field for an observer located
between the charges of Fig. 4.4.2a, in the neighborhood of the origin.
We now confine interest to distances from the origin that are small
compared to the charge spacing d. Effectively, the charges are at
infinity in the +z and -z directions, respectively.

With the help of Fig. 4.4.4 and the three-dimensional Pythagorean
theorem, the distances from the charges to the observer point are
expressed in spherical coordinates as
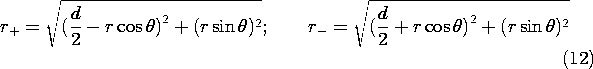
In these expressions, d is large compared to r, so they can be
expanded by again using (7) and keeping only linear terms in r.
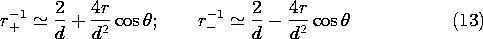
Introduction of these approximations into (2) results in the desired
expression for the potential associated with charges that are at
infinity on the z axis.

Note that z = r cos 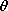 , so what appears to be a complicated
field in spherical coordinates is simply
, so what appears to be a complicated
field in spherical coordinates is simply

The z coordinate can just as well be regarded as Cartesian, and the
electric field evaluated using the gradient operator in Cartesian
coordinates. Thus, the surfaces of constant potential, shown in
Fig. 4.4.2c, are horizontal planes. It follows that the electric field
intensity is uniform and downward directed. Note that the electric
field that follows from (15) is what is obtained by direct
evaluation of (1.3.12) as the field of point charges q at a distance
d/2 above and below the point of interest.
Other Charge Singularities
A two-dimensional dipole consists of a pair
of oppositely charged parallel lines, rather than a pair of point
charges. Pictured in a plane perpendicular to the lines, and in polar
coordinates, the equipotentials appear similar to those of
Fig. 4.4.2b. However, in three dimensions the surfaces are cylinders of
circular cross-section and not at all like the closed surfaces of
revolution that are the equipotentials for the three-dimensional
dipole. Two-dimensional dipole fields are derived in Probs. 4.4.1
and 4.4.2, where the potentials are given for reference.
There is an infinite number of charge singularities. One of the
"higher order" singularities is illustrated by the quadrupole fields
developed in Probs. 4.4.3 and 4.4.4. We shall see these same
potentials again in Chap. 5.
4.5 Solution of Poisson's Equation for Specified ChargeDistributions
The superposition principle is now used to find the solution of
Poisson's equation for any given charge distribution  (r ).
The argument presented in the previous section for singular charge
distributions suggests the approach.
(r ).
The argument presented in the previous section for singular charge
distributions suggests the approach.

For the purpose of representing the arbitrary charge density
distribution as a sum of "elementary" charge distributions, we
subdivide the space occupied by the charge density into elementary
volumes of size dx'dy'dz'. Each of these elements is denoted by the
Cartesian coordinates (x',y',z'), as shown in Fig. 4.5.1. The charge
contained in one of these elementary volumes, the one with the
coordinates (x',y',z'), is
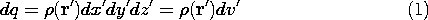
We now express the total potential due to the charge density  as
the superposition of the potentials d
as
the superposition of the potentials d due to the differential
elements of charge, (1), positioned at the points r'. Note that
each of these elementary charge distributions has zero charge density
at all points outside of the volume element dv' situated at
r'. Thus, they represent point charges of magnitudes dq
given by (1). Provided that |r - r'| is taken as the
distance between the point of observation r and the position of
one incremental charge r', the potential associated with this
incremental charge is given by (4.4.1).
due to the differential
elements of charge, (1), positioned at the points r'. Note that
each of these elementary charge distributions has zero charge density
at all points outside of the volume element dv' situated at
r'. Thus, they represent point charges of magnitudes dq
given by (1). Provided that |r - r'| is taken as the
distance between the point of observation r and the position of
one incremental charge r', the potential associated with this
incremental charge is given by (4.4.1).
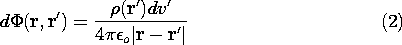
where in Cartesian coordinates
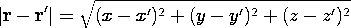
Note that (2) is a function of two sets of Cartesian
coordinates: the (observer) coordinates (x,y,z) of the point r at
which the potential is evaluated and the (source) coordinates
(x',y',z') of the point r' at which the incremental charge is
positioned.
According to the superposition principle, we obtain the total
potential produced by the sum of the differential charges by adding
over all differential potentials, keeping the observation point
(x,y,z) fixed. The sum over the differential volume elements becomes
a volume integral over the coordinates (x' , y' , z' ).

This is the superposition integral for the electroquasistatic
potential.
The evaluation of the potential requires that a triple
integration be carried out. With the help of a computer, or even a
programmable calculator, this is a straightforward process.
There are few examples where the three successive integrations are
carried out analytically without considerable difficulty.
There are special representations of (3),
appropriate in cases where the charge distribution is confined to
surfaces, lines, or where the distribution is two dimensional. For
these, the number of integrations is reduced to two or even one, and
the difficulties in obtaining analytical expressions are greatly
reduced.
Three-dimensional charge distributions can be represented as the
superposition of lines and sheets of charge and, by exploiting the
potentials found analytically for these distributions, the numerical
integration that might be required to determine the potential for a
three-dimensional charge distribution can be reduced to two or even
one numerical integration.
Superposition Integral for Surface Charge Density
If the charge density is confined to regions that can be described
by surfaces having a very small thickness  , then one of the three
integrations of (3) can be carried out in general. The situation is
as pictured in Fig. 4.5.2, where the distance to the observation
point is large compared to the thickness over which the charge is
distributed. As the integration of (3) is carried out over this
thickness
, then one of the three
integrations of (3) can be carried out in general. The situation is
as pictured in Fig. 4.5.2, where the distance to the observation
point is large compared to the thickness over which the charge is
distributed. As the integration of (3) is carried out over this
thickness  , the distance between source and observer, |r -
r'|, varies little. Thus, with
, the distance between source and observer, |r -
r'|, varies little. Thus, with 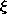 used to denote a
coordinate that is locally perpendicular to the surface, the general
superposition integral, (3), reduces to
used to denote a
coordinate that is locally perpendicular to the surface, the general
superposition integral, (3), reduces to
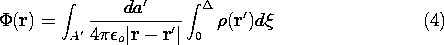

The integral on 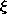 is by definition the surface charge density. Thus,
(4) becomes a form of the superposition integral applicable where
the charge distribution can be modeled as being on a surface.
is by definition the surface charge density. Thus,
(4) becomes a form of the superposition integral applicable where
the charge distribution can be modeled as being on a surface.

The following example illustrates the application of this
integral.
Example 4.5.1. Potential of a Uniformly Charged Disk
The disk shown in Fig. 4.5.3 has a radius R and carries a uniform
surface charge density  o. The following steps lead to the potential
and field on the axis of the disk.
o. The following steps lead to the potential
and field on the axis of the disk.

The distance |r - r'| between the point r' at radius  and angle
and angle  (in cylindrical coordinates) and the point r on
the axis of the disk (the z axis) is given by
(in cylindrical coordinates) and the point r on
the axis of the disk (the z axis) is given by

It follows that (5) is expressible in terms of the following double
integral
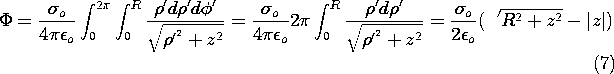
where we have allowed for both positive z, the case illustrated in the
figure, and negative z. Note that these are points on opposite sides
of the disk.
The axial field intensity Ez can be found by taking the gradient of
(7) in the z direction.
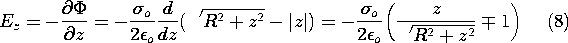
The upper sign applies to positive z, the lower sign to negative z.
The potential distribution of (8) can be checked in two
limiting cases for which answers are easily obtained by inspection:
the potential at a distance |z| \gg R, and the field at |z| \ll R.
observation from the
disk, the radius of the disk R is small compared to |z|, and the
potential of the disk must approach the potential of a point charge of
magnitude equal to the total charge of the disk,  o
o R2.
The potential given by (7) can be expanded in powers of R/z
R2.
The potential given by (7) can be expanded in powers of R/z
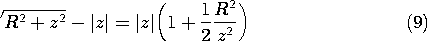
to find that  indeed approaches the potential function
indeed approaches the potential function

of a point charge at distance |z| from the observation point.
| (a) | At a very large distance |z| of the point of
|
| (b) | At |z| \ll R, on either side of the disk, the
field of the disk must
approach that of a charge sheet of very large (infinite) extent. But
that field is \pm  o /2 o /2 o. We find, indeed, that in the
limit |z| o. We find, indeed, that in the
limit |z| 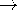 0, (8) yields this limiting result. 0, (8) yields this limiting result.
|
Superposition Integral for Line Charge Density
Another special case of the general superposition integral, (3),
pertains to fields from
charge distributions that are confined to the neighborhoods of lines.
In practice, dimensions of interest are large compared to the
cross-sectional dimensions of the area A' of the charge distribution.
In that case, the situation is as depicted in Fig. 4.5.4, and in the
integration over the cross-section the distance from source to
observer is essentially constant. Thus, the superposition integral,
(3), becomes
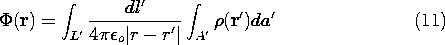

In view of the definition of the line charge density, (1.3.10),
this expression becomes

Example 4.5.2. Field of Collinear Line Charges of Opposite
Polarity
A positive line charge density of magnitude 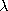 o is uniformly
distributed along the z axis between the points z = d and z =
3d. Negative charge of the same magnitude is distributed between z
= -d and z = -3d. The axial symmetry suggests the use of the
cylindrical coordinates defined in Fig. 4.5.5.
o is uniformly
distributed along the z axis between the points z = d and z =
3d. Negative charge of the same magnitude is distributed between z
= -d and z = -3d. The axial symmetry suggests the use of the
cylindrical coordinates defined in Fig. 4.5.5.

The distance from an element of charge 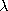 o dz' to an
arbitrary observer point (r, z) is
o dz' to an
arbitrary observer point (r, z) is
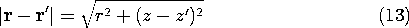
Thus, the line charge form of the superposition integral, (12),
becomes
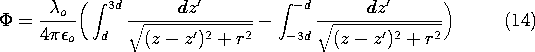
These integrations are carried out to obtain the desired potential
distribution
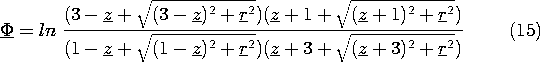
Here, lengths have been normalized to d, so that \un z = z/d and
\un r = r/d. Also, the potential has been normalized such that


A programmable calculator can be used to evaluate (15), given values
of (\un r, \un z). The equipotentials in Fig. 4.5.6 were, in fact,
obtained in
this way, making it possible to sketch the lines of field intensity
shown. Remember, the configuration is axisymmetric, so the
equipotentials are surfaces generated by rotating the cross-section
shown about the z axis.
Two-Dimensional Charge and Field Distributions
In two-dimensional configurations, where the charge
distribution
uniformly extends from z = - to z = +\infty, one of the
three integrations of the general superposition integral is carried
out by representing the charge by a superposition of line charges,
each extending from z = -
to z = +\infty, one of the
three integrations of the general superposition integral is carried
out by representing the charge by a superposition of line charges,
each extending from z = - to z = +\infty. The
fundamental element of charge, shown in Fig. 4.5.7, is not the point
charge of (1) but rather an infinitely long line charge. The
associated potential is not that of a point charge but rather of a
line charge.
to z = +\infty. The
fundamental element of charge, shown in Fig. 4.5.7, is not the point
charge of (1) but rather an infinitely long line charge. The
associated potential is not that of a point charge but rather of a
line charge.

With the line charge distributed along the z axis, the electric
field is given by (1.3.13) as

and integration of this expression gives the potential

where ro is a reference radius brought in as a constant of
integration. Thus, with da denoting an area element in the plane
upon which the source and field depend and r and r' the
vector positions of the observer and source respectively in that
plane, the potential for the incremental line charge of Fig. 4.5.7 is
written by making the identifications
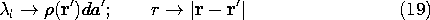
Integration over the given two-dimensional source distribution then
gives as the two-dimensional superposition integral
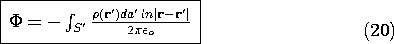
In dealing with charge distributions that extend to infinity in
the z direction, the potential at infinity can not be taken as a
reference. The potential at an arbitrary finite position can be
defined as zero by adding an integration constant to (20).
The following example leads to a result that will be found useful
in solving boundary value problems in Sec. 4.8.
Example 4.5.3. Two-Dimensional Potential of Uniformly
Charged Sheet
A uniformly charged strip lying in the y = 0 plane between x = x2
and x = x1 extends from z = +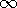 to z = -\infty, as shown in
Fig. 4.5.8. Because
the thickness of the sheet in the y direction is very small compared
to other dimensions of interest, the integrand of (20) is
essentially constant as the integration is carried out in the y
direction. Thus, the y integration amounts to a multiplication by the
thickness
to z = -\infty, as shown in
Fig. 4.5.8. Because
the thickness of the sheet in the y direction is very small compared
to other dimensions of interest, the integrand of (20) is
essentially constant as the integration is carried out in the y
direction. Thus, the y integration amounts to a multiplication by the
thickness  of the sheet
of the sheet

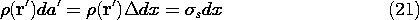
and (20) is written in terms of the surface charge density  s as
s as
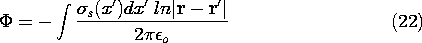
If the distance between source and observer is written in terms
of the Cartesian coordinates of Fig. 4.5.8, and it is recognized that
the surface charge density is uniform so that  s =
s =  o is
a constant, (22) becomes
o is
a constant, (22) becomes
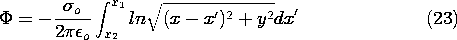
Introduction of the integration variable u = x - x' converts
this integral to an expression that is readily integrated.
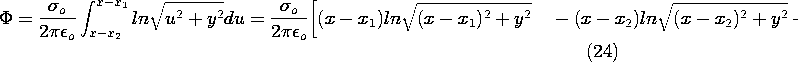
Two-dimensional distributions of surface charge can be
piece-wise approximated by uniformly charged planar segments. The
associated potentials are then represented by superpositions of the
potential given by (24).
Potential of Uniform Dipole Layer
The potential produced by a dipole of charges \pm q spaced a vector
distance d apart has been found to be given by (4.4.11)

where
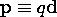
A dipole layer, shown in Fig. 4.5.9, consists of a pair of
surface charge distributions \pm  s spaced a distance d
apart. An area element da of such a layer, with the direction of
da (pointing from the negative charge density to the positive
one), can be regarded as a differential dipole producing a
(differential) potential d
s spaced a distance d
apart. An area element da of such a layer, with the direction of
da (pointing from the negative charge density to the positive
one), can be regarded as a differential dipole producing a
(differential) potential d
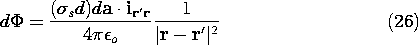
Denote the surface dipole density by  s where
s where

and the potential produced by a surface dipole distribution over the
surface S is given by

This potential can be interpreted particularly simply if the dipole
density is constant. Then  s can be pulled out from under the
integral, and there
s can be pulled out from under the
integral, and there  is equal to
is equal to  s /(4
s /(4
 o ) times the
integral
o ) times the
integral

This integral is dimensionless and has a simple geometric
interpretation. As shown in Fig. 4.5.9, ir' r  da is the area element projected into the direction connecting
the source point to the point of observation. Division by |r -
r'|2 reduces this projected area element onto the unit sphere.
Thus, the integrand is the differential solid angle subtended by
da as seen by an observer at r. The integral, (29), is equal
to the solid angle subtended by the surface S when viewed from the
point of observation r. In terms of this solid angle,
da is the area element projected into the direction connecting
the source point to the point of observation. Division by |r -
r'|2 reduces this projected area element onto the unit sphere.
Thus, the integrand is the differential solid angle subtended by
da as seen by an observer at r. The integral, (29), is equal
to the solid angle subtended by the surface S when viewed from the
point of observation r. In terms of this solid angle,


Next consider the discontinuity of potential in passing through the
surface S containing the dipole layer. Suppose that the surface
S is approached from the + side; then, from Fig. 4.5.10, the
surface is viewed under the solid angle \Omegao. Approached from
the other side, the surface subtends the solid angle -(4 -
\Omegao). Thus, there is a discontinuity of potential across the
surface of
-
\Omegao). Thus, there is a discontinuity of potential across the
surface of
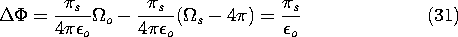
Because the dipole layer contains an infinite surface charge density
 s, the field within the layer is infinite. The "fringing"
field, i.e., the external field of the dipole layer, is finite and
hence negligible in the evaluation of the internal field of the
dipole layer. Thus, the internal field follows directly from Gauss'
law under the assumption that the field exists solely between the two
layers of opposite charge density (see Prob. 4.5.12). Because
contributions to (28) are dominated by
s, the field within the layer is infinite. The "fringing"
field, i.e., the external field of the dipole layer, is finite and
hence negligible in the evaluation of the internal field of the
dipole layer. Thus, the internal field follows directly from Gauss'
law under the assumption that the field exists solely between the two
layers of opposite charge density (see Prob. 4.5.12). Because
contributions to (28) are dominated by  s in the immediate
vicinity of a point r as it approaches the surface, the
discontinuity of potential is given by (31) even if
s in the immediate
vicinity of a point r as it approaches the surface, the
discontinuity of potential is given by (31) even if  s is a
function of position. In this case, the tangential E is
not continuous across the interface (Prob. 4.5.12).
s is a
function of position. In this case, the tangential E is
not continuous across the interface (Prob. 4.5.12).

4.6 Electroquasistatic Fields in the Presence of PerfectConductors
In most electroquasistatic situations, the surfaces of metals are
equipotentials. In fact, if surrounded by insulators, the surfaces of
many other conducting materials also tend to form equipotential
surfaces. The electrical properties and dynamical conditions required
for representing a boundary surface of a material by an equipotential
will be identified in Chap. 7.

Consider the situation shown in Fig. 4.6.l, where three surfaces Si,
i = 1, 2, 3 are held at the potentials  1,
1,  2, and
2, and
 3, respectively. These
are presumably the surfaces of conducting electrodes. The field in
the volume V surrounding the surfaces Si and extending to infinity is
not only due to the charge in that volume but due to charges outside
that region as well. Fields normal to the boundaries terminate on
surface charges. Thus, as far as the fields in the region of
interest are concerned, the sources are the charge density in the
volume V (if any) and the surface charges on the surrounding
electrodes.
3, respectively. These
are presumably the surfaces of conducting electrodes. The field in
the volume V surrounding the surfaces Si and extending to infinity is
not only due to the charge in that volume but due to charges outside
that region as well. Fields normal to the boundaries terminate on
surface charges. Thus, as far as the fields in the region of
interest are concerned, the sources are the charge density in the
volume V (if any) and the surface charges on the surrounding
electrodes.
The superposition integral, which is a solution to Poisson's
equation, gives the potential when the volume and surface charges are
known. In the present statement of the problem, the volume charge
densities are known in V, but the surface charge densities are not.
The only fact known about the latter is that they must be so
distributed as to make the Si's into equipotential surfaces at the
potentials  i.
i.
The determination of the charge distribution for the set of
specified equipotential surfaces is not a simple matter and will
occupy us in Chap. 5. But many interesting physical situations are
uncovered by a different approach. Suppose we are given a potential
function  (r ).
Then any equipotential surface of that potential can
be replaced by an electrode at the corresponding potential. Some of
the electrode configurations and associated fields obtained in this
manner are of great practical interest.
(r ).
Then any equipotential surface of that potential can
be replaced by an electrode at the corresponding potential. Some of
the electrode configurations and associated fields obtained in this
manner are of great practical interest.
Suppose such a procedure has been followed. To determine the
charge on the i-th electrode, it is necessary to integrate the surface
charge density over the surface of the electrode.
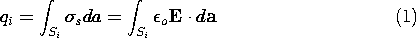
In the volume V, the contributions of the surface charges on the
equipotential surfaces are exactly equivalent to those of the charge
distribution inside the regions enclosed by the surface Si causing
the original potential function. Thus, an alternative to the use of
(1) for finding the total charge on the electrode is

where Vi is the volume enclosed by the surface Si and
 is the charge density inside Si associated with the
original potential.
is the charge density inside Si associated with the
original potential.
Capacitance
Suppose the system consists of only two electrodes,
as shown in Fig. 4.6.2. The charges on the surfaces of conductors (1)
and (2) can be evaluated from the assumedly known solution by using
(1).

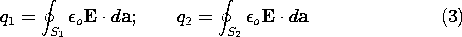
Further, there is a charge at infinity of
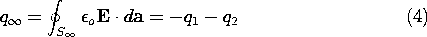
The charge at infinity is the negative of the sum of the charges on
the two electrodes. This follows from the fact that the field is
divergence free, and all field lines originating from q1 and
q2 must terminate at infinity. Instead of the charges, one could
specify the potentials of
the two electrodes with respect to infinity. If the charge on
electrode 1 is brought to it by a voltage source (battery) that takes
charge away from electrode 2 and deposits it on electrode 1, the
normal process of charging up two electrodes, then q1 = -q2. A
capacitance C between the two electrodes can be defined as the
ratio of charge on electrode 1 divided by the voltage between the two
electrodes. In terms of the fields, this definition becomes

In order to relate this definition to the capacitance concept used in
circuit theory, one further observation must be made. The capacitance
relates the charge of one electrode to the voltage between the two
electrodes. In general, there may also exist a voltage between
electrode 1 and infinity. In this case, capacitances must also be
assigned to relate the voltage with regard to infinity to the charges
on the electrodes. If the electrodes are to behave as the single
terminal-pair element of circuit theory, these capacitances must be
negligible. Returning to (5), note that C is independent of the
magnitude of the field variables. That is, if the magnitude of the
charge distribution is doubled everywhere, it follows from the
superposition integral that the potential doubles as well. Thus,
the electric field in the numerator and denominator of
(3) is doubled everywhere. Each of the integrals
therefore also doubles, their ratio remaining constant.
Example 4.6.1. Capacitance of Isolated Spherical Electrodes
A spherical electrode having radius a has a well-defined
capacitance C relative to an electrode at infinity. To determine
C, note that the equipotentials of a point charge q at the origin

are spherical. In fact, the equipotential having radius r = a has a
voltage with respect to infinity of

The capacitance is defined as the the net charge on the surface of the
electrode per unit voltage, (5). But the net charge found by
integrating the surface charge density over the surface of the sphere
is simply q, and so the capacitance follows from (7) as

By way of illustrating the conditions necessary for the
capacitance to be well defined, consider a pair of
spherical electrodes. Electrode (1) has radius a while electrode (2)
has radius R. If these are separated by many times the larger of
these radii, the potentials in their vicinities will again take the
form of (6). Thus, with the voltages v1 and v2 defined relative to
infinity, the charges on the respective spheres are
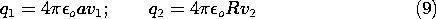
With all of the charge on sphere (1) taken from sphere (2),
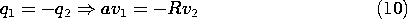
Under this condition, all of the field lines from sphere (1) terminate
on sphere (2). To determine the capacitance of the electrode pair, it
is necessary to relate the charge q1 to the voltage difference between
the spheres. To this end, (9) is used to write
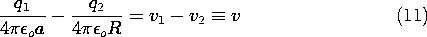
and because q1 = -q2, it follows that
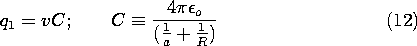
where C is now the capacitance of one sphere relative to the other.
Note that in order to maintain no net charge on the two spheres,
it follows from (9), (10), and (12) that the average of the voltages
relative to infinity must be retained at
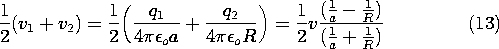
Thus, the average potential must be raised in proportion to the
potential difference v.
Example 4.6.2. Field and Capacitance of Shaped Electrodes
The field due to oppositely charged collinear line charges was
found to be (4.5.15) in Example 4.5.2. The equipotential surfaces,
shown in cross-section in Fig. 4.5.6, are melon shaped and tend to
enclose one or the other of the line charge elements.
Suppose that the surfaces on which the normalized potentials are
equal to 1 and to 0, respectively, are turned into electrodes, as shown
in Fig. 4.6.3. Now the field lines originate on positive surface
charges on the upper electrode and terminate on negative charges on
the ground plane. By contrast with the original field from the line
charges, the field in the region now inside the electrodes is zero.

One way to determine the net charge on one of the electrodes
requires that the electric field be found by taking the gradient of
the potential, that the unit normal vector to the surface of the
electrode be determined, and hence that the surface charge be
determined by evaluating  o E
o E  da on the electrode
surface. Integration of this
quantity over the electrode surface then gives the net charge. A
far easier way to determine this net charge is to recognize that it is
the same as the net charge enclosed by this surface for the original
line charge configuration. Thus, the net charge is simply
2d
da on the electrode
surface. Integration of this
quantity over the electrode surface then gives the net charge. A
far easier way to determine this net charge is to recognize that it is
the same as the net charge enclosed by this surface for the original
line charge configuration. Thus, the net charge is simply
2d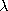 l, and if
the potentials of the respective electrodes are taken as \pm V, the
capacitance is
l, and if
the potentials of the respective electrodes are taken as \pm V, the
capacitance is

For the surface of the electrode in Fig. 4.6.3,
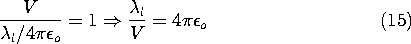
It follows from these relations that the desired capacitance is simply

In these two examples, the charge density is zero everywhere between
the electrodes. Thus, throughout the region of interest, Poisson's
equation reduces to Laplace's equation.

The solution to Poisson's equation throughout all space is tantamount
to solving Laplace's equation in a limited region, subject to certain
boundary conditions. A more direct approach to finding such solutions
is taken in the next chapter. Even then, it is well to keep in mind
that solutions to Laplace's equation in a limited region are solutions
to Poisson's equation throughout the entire space, including those
regions that contain the charges.
The next example leads to an often-used result, the capacitance
per unit length of a two-wire transmission line.
Example 4.6.3. Potential of Two Oppositely Charged
Conducting Cylinders
The potential distribution between two equal and opposite
parallel line charges has circular cylinders for its equipotential
surfaces. Any pair of these cylinders can be replaced by perfectly
conducting surfaces so as to obtain the
solution to the potential set up between two perfectly conducting
parallel cylinders of circular cross-section.

We proceed in the following ways: (a) The potentials produced by
two oppositely charged parallel lines positioned at x = +a and x =
-a, respectively, as shown in Fig. 4.6.4, are superimposed. (b) The
intersections of the equipotential surfaces with the x - y plane are
circles. The above results are used to find the potential
distribution produced by two parallel circular cylinders of radius R
with their centers spaced by a distance 2l. (c) The cylinders carry a
charge per unit length 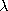 l and have a potential difference V,
and so their capacitance per unit length is determined.
l and have a potential difference V,
and so their capacitance per unit length is determined.
(a) The potential associated with a single line charge on the z axis is
most easily obtained by integrating the electric field, (1.3.13),
found from Gauss' integral law. It follows by superposition that the
potential for two parallel line charges of charge per unit length
+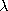 l and -
l and -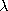 l, positioned at x = +a and x = -a,
respectively, is
l, positioned at x = +a and x = -a,
respectively, is
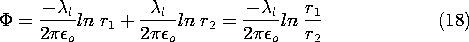
Here r1 and r2 are the distances of the field point P from
the + and - line charges, respectively, as shown in Fig. 4.6.4.
(b) On an equipotential surface,  = U is a constant and the
equation for that surface, (18), is
= U is a constant and the
equation for that surface, (18), is

where in Cartesian coordinates

With the help of Fig. 4.6.4, (19) is seen to
represent cylinders of circular cross-section with centers on the x
axis. This becomes apparent when the equation is expressed
in Cartesian coordinates. The equipotential circles are shown in
Fig. 4.6.5 for different values of


(c) Given two conducting cylinders whose centers are
a distance 2l apart, as shown in Fig. 4.6.6, what is the location of
the two line charges such that their field has equipotentials
coincident with these two cylinders? In terms of k as defined by
(20), (19) becomes


This expression can be written as a quadratic function of x and y.
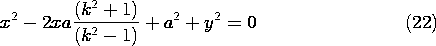
Equation (22) confirms that the loci of constant potential
in the x - y plane are indeed circles. In order
to relate the radius and location of these circles to the parameters
a and k, note that the
expression for a circle having radius R and center on the x axis at
x = l is
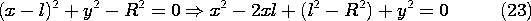
We can make (22) identical to this expression by setting

and

Given the spacing 2l and radius R of parallel conductors, this last
expression can be used to locate the positions of the line charges.
It also can be used to see that (l - a) = R2/(l + a), which can be
used with (24) solved for k2 to deduce that

Introduction of this expression into (20) then relates the potential
of the cylinder on the right to the line charge density. The
net charge per unit length that is actually on the surface of the
right conductor is equal to the line charge density 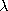 l.
With the voltage difference between the cylinders defined as V = 2U,
we can therefore solve for the capacitance per unit length.
l.
With the voltage difference between the cylinders defined as V = 2U,
we can therefore solve for the capacitance per unit length.
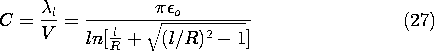
Often, the cylinders are wires and it is appropriate to approximate
this result for large ratios of l/R.
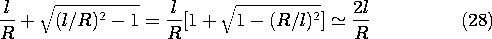
Thus, the capacitance per unit length is approximately

This same result can be obtained directly from (18) by recognizing
that when a \gg l, the line charges are essentially at the center of
the cylinders. Thus, evaluated on the surface of the right cylinder
where the potential is V/2, r1 \simeq R and r2 \simeq 2l,
(18) gives (29).
Example 4.6.4. Attraction of a Charged Particle to a
Neutral Sphere
A charged particle facing a conducting sphere induces a surface
charge distribution on the sphere. This distribution adjusts itself
so as to make the spherical surface an equipotential. In this
problem, we take advantage of the fact that two charges of opposite
sign produce a potential distribution, one equipotential surface of
which is a sphere.
First we find the potential distribution set up by a perfectly
conducting sphere of radius R, carrying a net charge Q, and a point
charge q at a distance X (X \geq R) from the center of the
sphere. Then the result is used to determine the force on the charge
q exerted by a neutral sphere (Q = 0)! The configuration
is shown in Fig. 4.6.7.

Consider first the potential distribution set up by a point
charge Q1 and another point charge q. The construction of the
potential is familiar from Sec. 4.4.
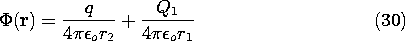
In general, the equipotentials are not spherical. However, the
surface of zero potential
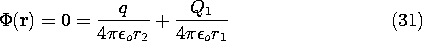
is described by

and if q/Q1  0, this represents a sphere. This can be proven
by expressing (32) in Cartesian coordinates and noting that in the
plane of the two charges, the result is the equation of a circle with
its center on the axis intersecting the two charges [compare (19)].
0, this represents a sphere. This can be proven
by expressing (32) in Cartesian coordinates and noting that in the
plane of the two charges, the result is the equation of a circle with
its center on the axis intersecting the two charges [compare (19)].
Using this fact, we can apply (32) to the points A and B in
Fig. 4.6.7 and
eliminate q/Q1. Taking R as the radius of the sphere and D as the
distance of the point charge Q1 from the center of the sphere, it
follows that
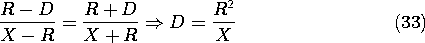
This specifies the distance D of the point charge Q1 from the center
of the equipotential sphere. Introduction of this result into (32)
applied to point A gives the (fictitious) charge Q1.

With this value for Q1 located in accordance with (33), the
surface of the sphere has zero potential. Without altering its
equipotential character, the potential of the sphere can be shifted by
positioning another fictitious charge at its center. If the net
charge of the spherical conductor is to be Q, then a charge Qo = Q
- Q1 is to be
positioned at the center of the sphere. The net field retains the
sphere as an equipotential surface, now of nonzero potential. The
field outside the sphere is the sought-for solution. With r3 defined
as the distance from the center of the sphere to the point of
observation, the field outside the sphere is
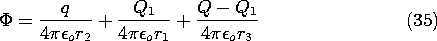
With Q = 0, the force on the charge follows from an evaluation of the
electric field intensity directed along an axis passing through the
center of the sphere and the charge q. The self-field of
the charge is omitted from this calculation. Thus, along the x axis
the potential due to the fictitious charges within the sphere is
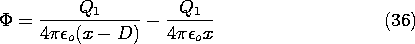
The x directed electric field intensity, and hence the required force,
follows as
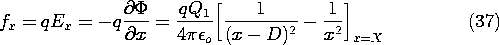
In view of (33) and (34), this can be written in terms of the actual
physical quantities as
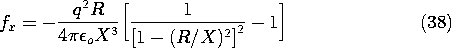
The field implied by (34) with Q = 0 is shown in Fig. 4.6.8. As the
charge approaches the spherical conductor, images are induced on the
nearest parts of the surface. To keep the net charge zero, charges of
opposite sign must be induced on parts of the surface that are more
remote from the point charge. The force of attraction results because
the charges of opposite sign are closer to the point charge than those
of the same sign.

4.7 Method of Images
Given a charge distribution throughout all of space, the
superposition integral can be used to determine the potential that
satisfies Poisson's equation. However, it is often the case that
interest is confined to a limited region, and the potential must
satisfy a boundary condition on surfaces bounding this region. In the
previous section, we recognized that any equipotential surface could
be replaced by a physical electrode, and found solutions to boundary
value problems in this way. The art of solving problems in this
"backwards" fashion can be remarkably practical but hinges on having
a good grasp of the relationship between fields and sources.
Symmetry is often the basis for superimposing fields to satisfy
boundary conditions. Consider for example the field of a point charge
a distance d/2 above a plane conductor, represented by an
equipotential. As illustrated in Fig. 4.7.1a, the field E+ of the
charge by itself has a component tangential to the boundary, and hence
violates the boundary condition on the surface of the conductor.
 To satisfy this condition, forget the conductor and consider the
field of two charges of equal magnitude and opposite signs, spaced a
distance 2d apart. In the symmetry plane, the normal components add
while the tangential components cancel. Thus, the composite field is
normal to the symmetry plane, as illustrated in the figure. In fact,
the configuration is the same as discussed in Sec. 4.4. The fields
are as in Fig. 4.4.2a, where now the planar
To satisfy this condition, forget the conductor and consider the
field of two charges of equal magnitude and opposite signs, spaced a
distance 2d apart. In the symmetry plane, the normal components add
while the tangential components cancel. Thus, the composite field is
normal to the symmetry plane, as illustrated in the figure. In fact,
the configuration is the same as discussed in Sec. 4.4. The fields
are as in Fig. 4.4.2a, where now the planar  = 0 surface is
replaced by a conducting sheet.
= 0 surface is
replaced by a conducting sheet.
This method of satisfying the boundary conditions imposed on the
field of a point charge by a plane conductor by using an opposite
charge at the mirror image position of the original charge, is called
the method of images. The charge of opposite sign at the
mirror-image position is the "image-charge."
Any superposition of charge pairs of opposite sign placed
symmetrically on two sides of a plane results in a field that is
normal to the plane. An example is the field of the pair of
line charge elements shown in Fig. 4.5.6. With an electrode having the
shape of the equipotential enclosing the upper line charge and a
ground plane in the plane of symmetry, the field is as shown in
Fig. 4.6.3. This identification of a physical
situation to go with a known field was used in the previous
section. The method of images is only a special case involving planar
equipotentials.
To compare the replacement of the symmetry plane by a planar
conductor, consider the following demonstration.
\begindemo1Charge Induced in Ground Plane by Overhead
Conductor
The circular cylindrical conductor of Fig. 4.7.2,
separated by a
distance l from an equipotential (grounded) metal surface, has a
voltage U = Uo cos  t.
The field between the conductor and the ground
plane is that of a line charge inside the conductor and its image
below the ground plane. Thus, the potential is that determined in
Example 4.6.3. In the Cartesian coordinates shown, (4.6.18), the
definitions of r1 and r2 with (4.6.19) and (4.6.25) (where U =
V/2) provide the potential distribution
t.
The field between the conductor and the ground
plane is that of a line charge inside the conductor and its image
below the ground plane. Thus, the potential is that determined in
Example 4.6.3. In the Cartesian coordinates shown, (4.6.18), the
definitions of r1 and r2 with (4.6.19) and (4.6.25) (where U =
V/2) provide the potential distribution

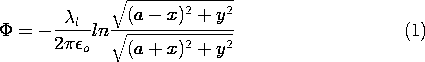
The charge per unit length on the cylinder is [compare (4.6.27)]
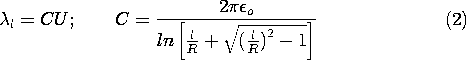
In the actual physical situation, images of this charge are
induced on the surface of the ground plane. These can be measured by
using a flat probe that is connected through the cable to ground and
insulated from the ground plane just below. The input resistance of
the oscilloscope is low enough so that the probe surface is at
essentially the same (zero) potential as the ground plane. What is
the measured current, and hence voltage vo, as a function of the
position Y of the probe?
Given the potential, the surface charge is (1.3.17)
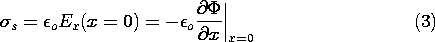
Evaluation of this expression using (1) gives
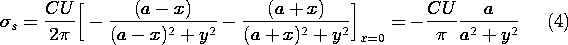
Conservation of charge requires that the probe current be the time
rate of change of the charge q on the probe surface.

Because the probe area is small, the integration of the surface charge
over its surface is approximated by the product of the area and the
surface charge evaluated at the position Y of its center.

Thus, it follows from (4)-(6) that the induced voltage, vo =
-Rsis, is
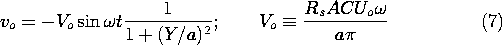
This distribution of the induced signal with probe position is shown
in Fig. 4.7.2.
In the analysis, it is assumed that the plane x = 0, including the
section of surface occupied by the probe, is constrained to zero
potential. In first computing the current to the probe using this
assumption and then finding the probe voltage, we are clearly making
an approximation that is valid only if the voltage is "small." This
can be insured by making the resistance Rs small.
The usual scope resistance is 1 M\Omega. It may come as a surprise
that such a resistance is treated here as a short. However, the
voltage given by (7) is proportional to the frequency, so the value
of acceptable resistance depends on the frequency. As the frequency is
raised to the point where the voltage of the probe does begin to
influence the field distribution, some of the field lines that
originally terminated on the electrode are diverted to the grounded
part of the plane. Also, charges of opposite polarity are induced on
the other side of the probe. The result is an output signal that no
longer increases with frequency. A frequency response of
the probe voltage that does not increase linearly with frequency is
therefore telltale evidence that the resistance
is too large or the frequency too high. In the demonstration, where
"desk-top" dimensions are typical, the frequency response is linear to
about 100 Hz with a scope resistance of 1 M\Omega.
As the frequency is raised, the system becomes one with two
excitations contributing to the potential distribution. The multiple
terminal-pair systems treated in Sec. 5.1 start to model the full
frequency response of the probe.
Symmetry also motivates the use of image charges to satisfy
boundary conditions on more than one planar surface. In Fig. 4.7.3,
the objective is to find the field of the point charge in the first
quadrant with the planes x = 0 and y = 0 at zero potential. One
image charge gives rise to a field that satisfies one of the boundary
conditions. The second is satisfied by introducing an image for the
pair of charges.

Once an image or a system of images has been found for a point
charge, the same principle of images can be used for a continuous
charge distribution. The charge density distributions have density
distributions of image charges, and the total field is again found
using the superposition integral.
Even where symmetry is not involved, charges located outside the
region of interest to produce fields that satisfy boundary conditions
are often referred to as image charges. Thus, the charge Q1 located
within the spherical electrode of Example 4.6.4 can be regarded as the
image of q.
4.8 Charge Simulation Approach to Boundary Value Problems
In solving a boundary value problem, we are in essence finding
that distribution of charges external to the region of interest that
makes the total field meet the boundary conditions. Commonly, these
external charges are actually on the surfaces of conductors bounding
or embedded in the region of interest. By way of preparation for the
boundary value point of view taken in the next chapter, we consider in
this section a direct approach to adjusting surface charges so that
the fields meet prescribed boundary conditions on the potential.
Analytically, the technique is cumbersome. However, with a computer,
it becomes one of a class of powerful numerical
techniques[1] for solving boundary value
problems.
Suppose that the fields are two dimensional, so that the region of
interest can be "enclosed" by a surface that can be approximated by
strip segments, as illustrated in Fig. 4.8.1a. This example becomes
an approximation to the circular conductor over a ground plane
(Example 4.7.1) if the magnitudes of the charges on the strips are
adjusted to make the surfaces approximate appropriate equipotentials.

With the surface charge density on each of these strips taken as
uniform, a "stair-step" approximation to the actual
distribution of charge is obtained. By increasing the number of
segments, the approximation is refined. For purposes of
illustration, we confine ourselves here to boundaries lying in planes
of constant y, as shown in Fig. 4.8.1b. Then the potential
associated with a single uniformly charged strip is as found in
Example 4.5.3.
Consider first the potential due to a strip of width (a)
lying in the plane y = 0 with its center at x = 0, as shown in
Fig. 4.8.2a. This is a special case of the configuration considered in
Example 4.5.3. It follows from (4.5.24) with x1 = a/2 and
x2 = -a/2 that the potential at the observer location (x, y) is


where
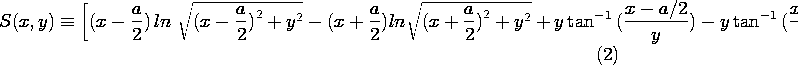
With the strip located at (x, y) = (X, Y), as shown in Fig. 4.8.2b,
this potential becomes
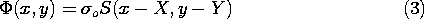
In turn, by superposition we can write the potential due to N such
strips, the one having the uniform surface charge density  i
being located at (x, y) = (Xi, Yi).
i
being located at (x, y) = (Xi, Yi).
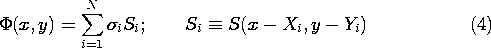
Given the surface charge densities,  i, the potential at any
given location (x, y) can be evaluated using this expression. We assume
that the net charge on the strips is zero, so that their collective
potential goes to zero at infinity.
i, the potential at any
given location (x, y) can be evaluated using this expression. We assume
that the net charge on the strips is zero, so that their collective
potential goes to zero at infinity.
With the strips representing surfaces that are constrained in
potential (for example, perfectly conducting boundaries), the charge
densities are adjusted to meet boundary conditions. Each strip
represents part of an electrode surface. The potential Vj at the
center of the j-th strip is set equal to the known voltage of the
electrode to which it belongs. Evaluating (4) for the center of the
j-th strip one obtains
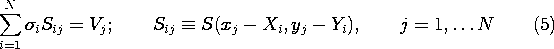
This statement can be made for each of the strips, so that it holds
with j = 1, \ldots N. These relations comprise N equations that
are linear in the N unknowns  1 \ldots
1 \ldots  N.
N.
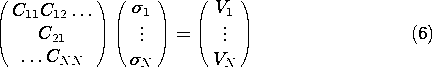
The potentials V1 \ldots VN on the right are known, so these
expressions can be solved for the surface charge densities. Thus, the
potential that meets the approximate boundary conditions, (4), has
been determined. We have found an approximation to the surface charge
density needed to meet the potential boundary condition.
Example 4.8.1. Fields of Finite Width Parallel Plate Capacitor
In Fig. 4.8.3, the parallel plates of a capacitor are divided
into six segments. The potentials at the centers of those in
the top row are required to be V/2, while those in the lower row are
-V/2. In this simple case of six segments, symmetry
gives

and the six equations in six unknowns, (6) with N = 6, reduces to two
equations in two unknowns. Thus, it
is straightforward to write analytical expressions for the surface
charge densities (See Prob. 4.8.1).
The equipotentials and associated
surface charge distributions are shown in Fig. 4.8.4 for increasing
numbers of charge sheets. The first is a reminder of the
distribution of potential for uniformly charged sheets. Shown
next are the equipotentials that result from using the six-segment
approximation just evaluated. In the last case, 20 segments have been
used and the inversion of (6) carried out by means of a computer.

Note that the approximate capacitance per unit length is

This section shows how the superposition integral
point of view can be the basis for a numerical approach to
solving boundary value problems. But as we proceed to a more direct
approach to boundary value problems, it is especially important to
profit from the physical insight inherent in the method used in
this section.
We have found a mathematical procedure for adjusting the
distributions of surface charge so that boundaries are equipotentials.
Conducting surfaces surrounded by insulating material tend to become
equipotentials by similarly redistributing their surface charge. For
example, consider how the surface charge redistributes itself on the
parallel plates of Fig. 4.8.4. With the surface charge uniformly
distributed, there is a strong electric field tangential to the
surface of the plate. In the upper plate, the charges move radially
outward in response to this tangential field. Thus, the charge
redistributes itself as shown in the subsequent cases. The correct
distribution of surface charge density is the one that makes this
tangential electric field approach zero, which it is when the
surfaces become equipotentials. Thus, the surface charge
density is higher near the edges of the plates than it is in
the middle. The additional surface charges near the edges result in
just that inward-directed electric field which is needed to make the
net field perpendicular to the surfaces of the electrodes.
We will find in Sec. 8.6 that the solution to a class of
two-dimensional MQS boundary value problems is completely analogous to
that for EQS systems of perfect conductors.
4.9 Summary
The theme in this chapter is set by the two equations that
determine E, given the charge density  . The first of these,
(4.0.1), requires that E be irrotational. Through the
representation of E as
the negative gradient of the electric potential,
. The first of these,
(4.0.1), requires that E be irrotational. Through the
representation of E as
the negative gradient of the electric potential,  , it is effectively
integrated.
, it is effectively
integrated.

This gradient operator, determined in Cartesian coordinates in Sec.
4.1 and found in cylindrical and spherical coordinates in the
problems of that section, is summarized in Table I. The associated
gradient integral theorem, (4.1.16), is added for reference to the
integral theorems of Gauss and Stokes in Table II.
The substitution of (1) into Gauss' law, the second of the two
laws forming the theme of this chapter, gives Poisson's equation.

The Laplacian operator on the left, defined as the divergence of the
gradient of  , is summarized in the three standard coordinate systems
in Table I.
, is summarized in the three standard coordinate systems
in Table I.
It follows from the linearity of (2) that the potential for the
superposition of charge distributions is the superposition of
potentials for the individual charge distributions. The potentials for
dipoles and other singular charge distributions are therefore found
by superimposing the potentials of point or line charges. The
superposition integral formalizes the determination of the potential,
given the distribution of charge. With the surface and line charges
recognized as special (singular) volume charge densities, the second
and third forms of the superposition integral summarized in Table
4.9.1 follow directly from the first. The fourth is convenient if
the source and field are two dimensional.
Through Sec. 4.5, the charge density is regarded as given
throughout all space. From Sec. 4.6 onward, a shift is made toward
finding the field in confined regions of space bounded by surfaces of
constant potential. At first, the approach is opportunistic. Given a
solution, what problems have been solved? However, the numerical
convolution method of Sec. 4.8 is a direct and practical approach to
solving boundary value problems with arbitrary geometry.


 by Gauss' law.
by Gauss' law.

 . In free space, the source of a
magnetoquasistatic field is a vector, the current density. Scalar
sources, are simpler than vector sources and this is why
electroquasistatic fields are taken up first.
. In free space, the source of a
magnetoquasistatic field is a vector, the current density. Scalar
sources, are simpler than vector sources and this is why
electroquasistatic fields are taken up first.
 .
But before the chapter ends, we will be finding fields in limited
regions bounded by conductors. In these more practical situations,
the distribution of charge on the boundary surfaces is not known
until after the fields have been determined. Thus, this chapter sets
the stage for the solving of boundary value problems in Chap. 5.
.
But before the chapter ends, we will be finding fields in limited
regions bounded by conductors. In these more practical situations,
the distribution of charge on the boundary surfaces is not known
until after the fields have been determined. Thus, this chapter sets
the stage for the solving of boundary value problems in Chap. 5.
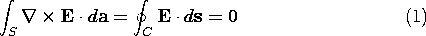

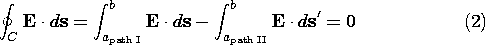
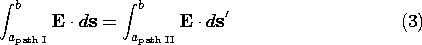
 (r ) to define this scalar function
(r ) to define this scalar function
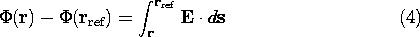

 r. With
r. With 
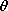
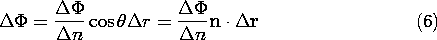


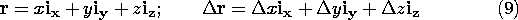
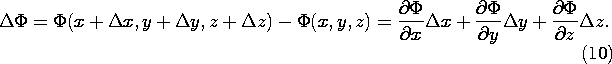
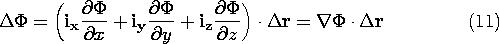
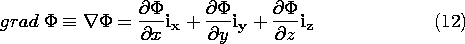
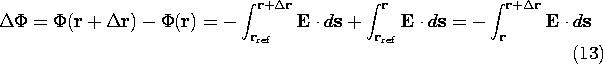


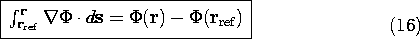



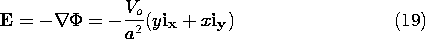
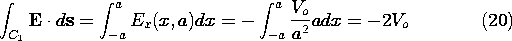
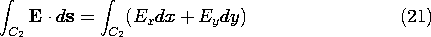
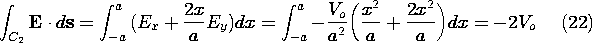

 . The
contour follows part of a straight line through the origin. In the
exterior region, integration gives
. The
contour follows part of a straight line through the origin. In the
exterior region, integration gives
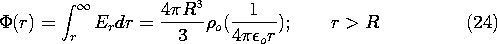
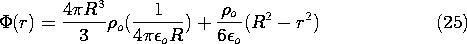
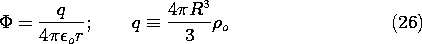


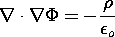

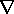 2, denoted by the second
form of (2) and called the Laplacian of
2, denoted by the second
form of (2) and called the Laplacian of 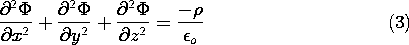


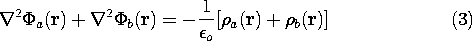
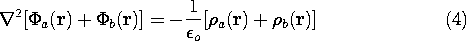
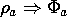





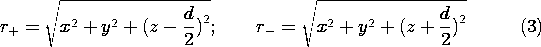
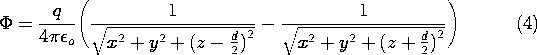
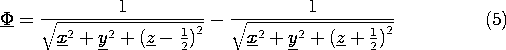
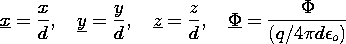

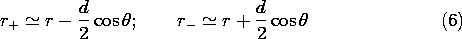

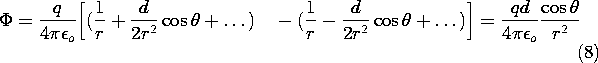
 /2, the
cosine decreases to zero, making it clear that the equipotential
must approach the origin. The equipotentials and associated lines of
E are shown in Fig. 4.4.2b.
/2, the
cosine decreases to zero, making it clear that the equipotential
must approach the origin. The equipotentials and associated lines of
E are shown in Fig. 4.4.2b.




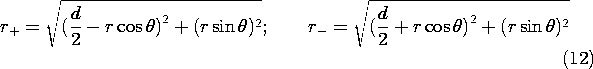
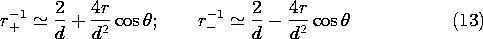



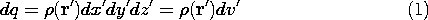
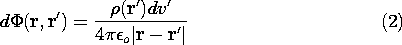
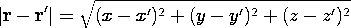

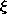 used to denote a
coordinate that is locally perpendicular to the surface, the general
superposition integral, (3), reduces to
used to denote a
coordinate that is locally perpendicular to the surface, the general
superposition integral, (3), reduces to
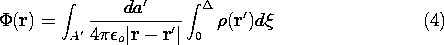


 o. The following steps lead to the potential
and field on the axis of the disk.
o. The following steps lead to the potential
and field on the axis of the disk.

 (in cylindrical coordinates) and the point r on
the axis of the disk (the z axis) is given by
(in cylindrical coordinates) and the point r on
the axis of the disk (the z axis) is given by

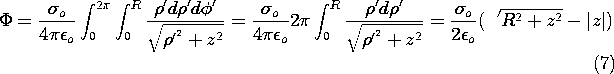
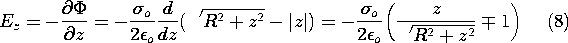
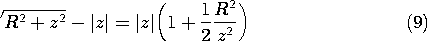

 o. We find, indeed, that in the
limit |z|
o. We find, indeed, that in the
limit |z|  0, (8) yields this limiting result.
0, (8) yields this limiting result.
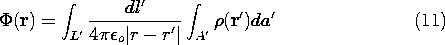


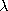 o is uniformly
distributed along the z axis between the points z = d and z =
3d. Negative charge of the same magnitude is distributed between z
= -d and z = -3d. The axial symmetry suggests the use of the
cylindrical coordinates defined in Fig. 4.5.5.
o is uniformly
distributed along the z axis between the points z = d and z =
3d. Negative charge of the same magnitude is distributed between z
= -d and z = -3d. The axial symmetry suggests the use of the
cylindrical coordinates defined in Fig. 4.5.5.

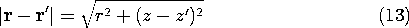
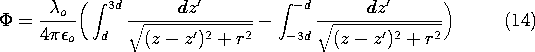
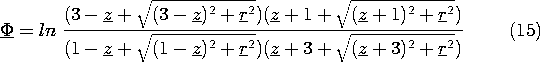





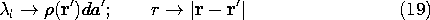
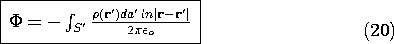

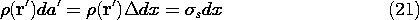
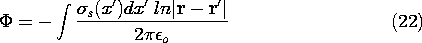
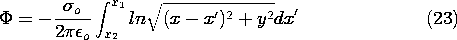
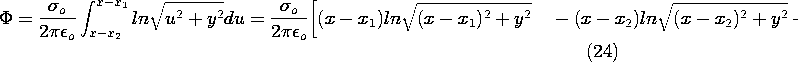

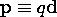
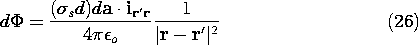



 da is the area element projected into the direction connecting
the source point to the point of observation. Division by |r -
r'|2 reduces this projected area element onto the unit sphere.
Thus, the integrand is the differential solid angle subtended by
da as seen by an observer at r. The integral, (29), is equal
to the solid angle subtended by the surface S when viewed from the
point of observation r. In terms of this solid angle,
da is the area element projected into the direction connecting
the source point to the point of observation. Division by |r -
r'|2 reduces this projected area element onto the unit sphere.
Thus, the integrand is the differential solid angle subtended by
da as seen by an observer at r. The integral, (29), is equal
to the solid angle subtended by the surface S when viewed from the
point of observation r. In terms of this solid angle,


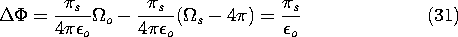


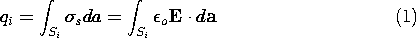


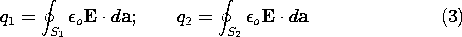
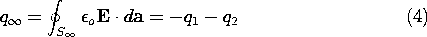




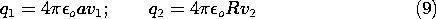
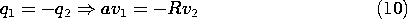
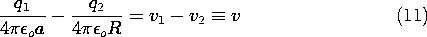
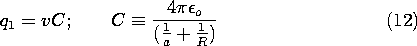
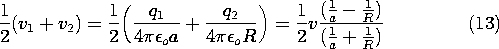


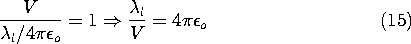



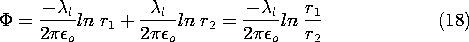






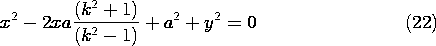
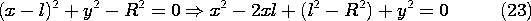



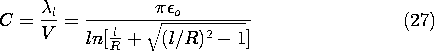
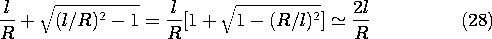


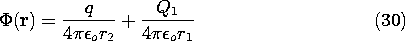
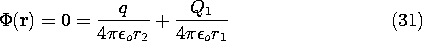

 0, this represents a sphere. This can be proven
by expressing (32) in Cartesian coordinates and noting that in the
plane of the two charges, the result is the equation of a circle with
its center on the axis intersecting the two charges [compare (19)].
0, this represents a sphere. This can be proven
by expressing (32) in Cartesian coordinates and noting that in the
plane of the two charges, the result is the equation of a circle with
its center on the axis intersecting the two charges [compare (19)].
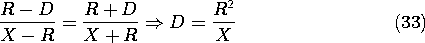

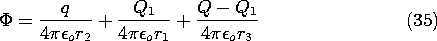
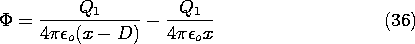
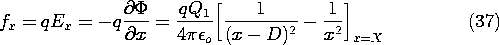
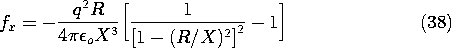


 t.
The field between the conductor and the ground
plane is that of a line charge inside the conductor and its image
below the ground plane. Thus, the potential is that determined in
Example 4.6.3. In the Cartesian coordinates shown, (4.6.18), the
definitions of r1 and r2 with (4.6.19) and (4.6.25) (where U =
V/2) provide the potential distribution
t.
The field between the conductor and the ground
plane is that of a line charge inside the conductor and its image
below the ground plane. Thus, the potential is that determined in
Example 4.6.3. In the Cartesian coordinates shown, (4.6.18), the
definitions of r1 and r2 with (4.6.19) and (4.6.25) (where U =
V/2) provide the potential distribution