5.1
Particular and Homogeneous Solutions to Poisson'sand Laplace's Equations

Suppose we want to analyze an electroquasistatic situation as shown in Fig. 5.1.1. A charge distribution (r) is specified in the part of space of interest, designated by the volume V. This region is bounded by perfect conductors of specified shape and location. Known potentials are applied to these conductors and the enclosing surface, which may be at infinity.

Figure 5.1.1 Volume of interest in which there can be a distribution of charge density. To illustrate bounding surfaces on which potential is constrained, n isolated surfaces and one enclosing surface are shown.

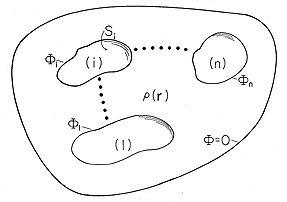
In the space between the conductors, the potential function obeys Poisson's equation, (5.0.2). A particular solution of this equation within the prescribed volume V is given by the superposition integral, (4.5.3).

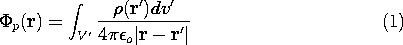
This potential obeys Poisson's equation at each point within the volume V. Since we do not evaluate this equation outside the volume V, the integration over the sources called for in (1) need include no sources other than those within the volume V. This makes it clear that the particular solution is not unique, because the addition to the potential made by integrating over arbitrary charges outside the volume V will only give rise to a potential, the Laplacian derivative of which is zero within the volume V.

Is (1) the complete solution? Because it is not unique, the answer must be, surely not. Further, it is clear that no information as to the position and shape of the conductors is built into this solution. Hence, the electric field obtained as the negative gradient of the potential _p of (1) will, in general, possess a finite tangential component on the surfaces of the electrodes. On the other hand, the conductors have surface charge distributions which adjust themselves so as to cause the net electric field on the surfaces of the conductors to have vanishing tangential electric field components. The distribution of these surface charges is not known at the outset and hence cannot be included in the integral (1).

A way out of this dilemma is as follows: The potential distribution we seek within the space not occupied by the conductors is the result of two charge distributions. First is the prescribed volume charge distribution leading to the potential function _p, and second is the charge distributed on the conductor surfaces. The potential function produced by the surface charges must obey the source-free Poisson's equation in the space V of interest. Let us denote this solution to the homogeneous form of Poisson's equation by the potential function _h. Then, in the volume V, _h must satisfy Laplace's equation.

The superposition principle then makes it possible to write the total potential as

The problem of finding the complete field distribution now reduces to that of finding a solution such that the net potential of (3) has the prescribed potentials v_i on the surfaces S_i. Now _p is known and can be evaluated on the surface S_i. Evaluation of (3) on S_i gives

so that the homogeneous solution is prescribed on the boundaries S_i.

Hence, the determination of an electroquasistatic field with prescribed potentials on the boundaries is reduced to finding the solution to Laplace's equation, (2), that satisfies the boundary condition given by (5).

The approach which has been formalized in this section is another point of view applicable to the boundary value problems in the last part of Chap. 4. Certainly, the abstract view of the boundary value situation provided by Fig. 5.1.1 is not different from that of Fig. 4.6.1. In Example 4.6.4, the field shown in Fig. 4.6.8 is determined for a point charge adjacent to an equipotential charge-neutral spherical electrode. In the volume V of interest outside the electrode, the volume charge distribution is singular, the point charge q. The potential given by (4.6.35), in fact, takes the form of (3). The particular solution can be taken as the first term, the potential of a point charge. The second and third terms, which are equivalent to the potentials caused by the fictitious charges within the sphere, can be taken as the homogeneous solution.

Superposition to Satisfy Boundary Conditions

In the following sections, superposition will often be used in another way to satisfy boundary conditions. Suppose that there is no charge density in the volume V, and again the potentials on each of the n surfaces S_j are v_j. Then

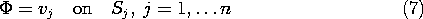
The solution is broken into a superposition of solutions _j that meet the required condition on the j-th surface but are zero on all of the others.

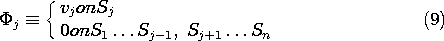
Each term is a solution to Laplace's equation, (6), so the sum is as well.

In Sec. 5.5, a method is developed for satisfying arbitrary boundary conditions on one of four surfaces enclosing a volume of interest.

Capacitance Matrix

Suppose that in the n electrode system the net charge on the i-th electrode is to be found. In view of (8), the integral of E da over the surface S_i enclosing this electrode then gives

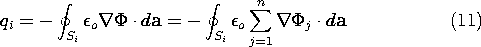
Because of the linearity of Laplace's equation, the potential _j is proportional to the voltage exciting that potential, v_j. It follows that (11) can be written in terms of capacitance parameters that are independent of the excitations. That is, (11) becomes

where the capacitance coefficients are

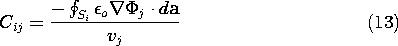
The charge on the i-th electrode is a linear superposition of the contributions of all n voltages. The coefficient multiplying its own voltage, C_ii, is called the self-capacitance, while the others, C_ij, i j, are the mutual capacitances.