Having investigated some general properties of solutions to Poisson's equation, it is now appropriate to study specific methods of solution to Laplace's equation subject to boundary conditions. Exemplified by this and the next section are three standard steps often used in representing EQS fields. First, Laplace's equation is set up in the coordinate system in which the boundary surfaces are coordinate surfaces. Then, the partial differential equation is reduced to a set of ordinary differential equations by separation of variables. In this way, an infinite set of solutions is generated. Finally, the boundary conditions are satisfied by superimposing the solutions found by separation of variables.
In this section, solutions are derived that are natural if boundary conditions are stated along coordinate surfaces of a Cartesian coordinate system. It is assumed that the fields depend on only two coordinates, x and y, so that Laplace's equation is (Table I)

This is a partial differential equation in two independent variables. One time-honored method of mathematics is to reduce a new problem to a problem previously solved. Here the process of finding solutions to the partial differential equation is reduced to one of finding solutions to ordinary differential equations. This is accomplished by the method of separation of variables. It consists of assuming solutions with the special space dependence

In (2), X is assumed to be a function of x alone and Y is a
function of y alone. If need be, a general space dependence is then
recovered by superposition of these special solutions. Substitution of
(2) into (1) and division by  then gives
then gives
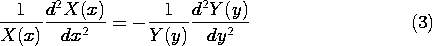
Total derivative symbols are used because the respective functions X and Y are by definition only functions of x and y.
In (3) we now have on the left-hand side a function of x alone, on the right-hand side a function of y alone. The equation can be satisfied independent of x and y only if each of these expressions is constant. We denote this "separation" constant by k2, and it follows that

and

These equations have the solutions
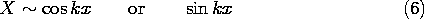
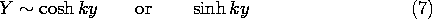
If k = 0, the solutions degenerate into
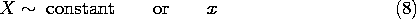
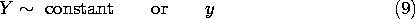
The product solutions, (2), are summarized in the first four rows of Table 5.4.1. Those in the right-hand column are simply those of the middle column with the roles of x and y interchanged. Generally, we will leave the prime off the k' in writing these solutions. Exponentials are also solutions to (7). These, sometimes more convenient, solutions are summarized in the last four rows of the table.
The solutions summarized in this table can be used to gain insight into the nature of EQS fields. A good investment is therefore made if they are now visualized.
The fields represented by the potentials in the left-hand column
of Table 5.4.1 are all familiar. Those that are linear in x and y
represent uniform fields, in the x and y directions, respectively.
The potential xy is familiar from Fig. 4.1.3. We will use similar
conventions to represent the potentials of the second column, but it
is helpful to have in mind the three-dimensional portrayal exemplified
for the potential xy in Fig. 4.1.4. In the more complicated field maps
to follow, the sketch is visualized as a contour map of the potential
 with peaks of positive potential and valleys of negative potential.
with peaks of positive potential and valleys of negative potential.
On the top and left peripheries of Fig. 5.4.1 are sketched the functions cos kx and cosh ky, respectively, the product of which is the first of the potentials in the middle column of Table 5.4.1. If we start out from the origin in either the +y or -y directions (north or south), we climb a potential hill. If we instead proceed in the +x or -x directions (east or west), we move downhill. An easterly path begun on the potential hill to the north of the origin corresponds to a decrease in the cos kx factor. To follow a path of equal elevation, the cosh ky factor must increase, and this implies that the path must turn northward.
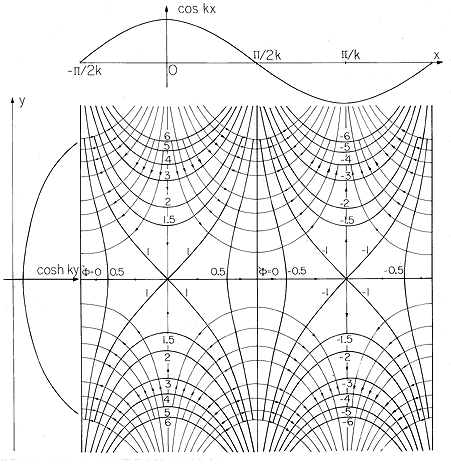
 = cos(kx)
cosh (ky) and field lines. As an aid to visualizing the potential,
the separate factors cos (kx) and cosh (ky) are, respectively,
displayed at the top and to the left.
= cos(kx)
cosh (ky) and field lines. As an aid to visualizing the potential,
the separate factors cos (kx) and cosh (ky) are, respectively,
displayed at the top and to the left.
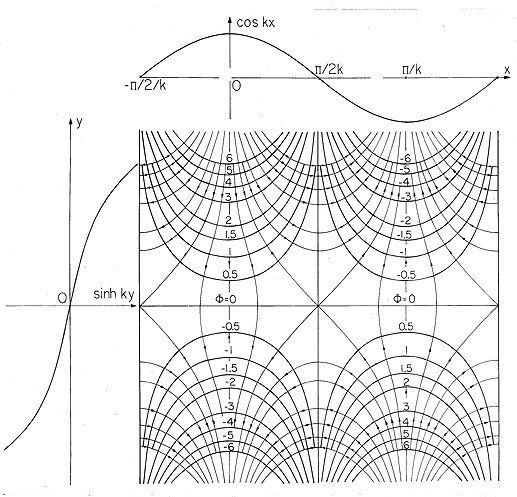
A good starting point in making these field sketches is the
identification of the contours of zero potential. In the plot of the
second potential in the middle column of Table 5.4.1, shown in
Fig. 5.4.2, these are the y axis and the lines kx = +  /2, +
3
/2, +
3 /2, etc. The
dependence on y is now odd rather than even, as it was for the plot of
Fig. 5.4.1. Thus, the origin is now on the side of a potential hill
that slopes downward from north to south.
/2, etc. The
dependence on y is now odd rather than even, as it was for the plot of
Fig. 5.4.1. Thus, the origin is now on the side of a potential hill
that slopes downward from north to south.
 = cos (kx)
sinh (ky) and field lines. As an aid to visualizing the potential,
the separate factors cos (kx) and sinh (ky) are, respectively,
displayed at the top and to the left.
= cos (kx)
sinh (ky) and field lines. As an aid to visualizing the potential,
the separate factors cos (kx) and sinh (ky) are, respectively,
displayed at the top and to the left.The solutions in the third and fourth rows of the second column possess the same field patterns as those just discussed provided those patterns are respectively shifted in the x direction. In the last four rows of Table 5.4.1 are four additional possible solutions which are linear combinations of the previous four in that column. Because these decay exponentially in either the +y or -y directions, they are useful for representing solutions in problems where an infinite half-space is considered.
The solutions in Table 5.4.1 are nonsingular throughout the
entire x-y plane. This means that Laplace's equation is obeyed
everywhere within the finite x-y plane, and hence the field lines are
continuous; they do not appear or disappear. The sketches show that
the fields become stronger and stronger as one proceeds in the
positive and negative y directions. The lines of electric field
originate on positive charges and terminate on negative charges at y
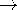

 .
Thus, for the plots shown in Figs. 5.4.1 and 5.4.2, the charge
distributions at infinity must consist of alternating distributions of
positive and negative charges of infinite amplitude.
.
Thus, for the plots shown in Figs. 5.4.1 and 5.4.2, the charge
distributions at infinity must consist of alternating distributions of
positive and negative charges of infinite amplitude.
Two final observations serve to further develop an appreciation for the nature of solutions to Laplace's equation. First, the third dimension can be used to represent the potential in the manner of Fig. 4.1.4, so that the potential surface has the shape of a membrane stretched from boundaries that are elevated in proportion to their potentials.
Laplace's equation, (1), requires that the sum of quantities that reflect the curvatures in the x and y directions vanish. If the second derivative of a function is positive, it is curved upward; and if it is negative, it is curved downward. If the curvature is positive in the x direction, it must be negative in the y direction. Thus, at the origin in Fig. 5.4.1, the potential is cupped downward for excursions in the x direction, and so it must be cupped upward for variations in the y direction. A similar deduction must apply at every point in the x-y plane.
Second, because the k that appears in the periodic functions of the second column in Table 5.4.1 is the same as that in the exponential and hyperbolic functions, it is clear that the more rapid the periodic variation, the more rapid is the decay or apparent growth.
| k = 0 | k2 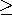 0 0 |
k2  0 (k 0 (k  jk') jk') |
|---|---|---|
| Constant | cos kx cosh ky | cosh k'x cos k'y |
| y | cos kx sinh ky | coshk'x sin k'y |
| x | sin kx cosh ky | sinh k'x cos k'y |
| xy | sin kx sinh ky | sinh k'x sin k'y |
| cos kx eky | ek'x cos k'y | |
| cos kx e-ky | e-k'x cos k'y | |
| sin kx eky | ek'x sin k'y | |
| sin kx e-ky | e-k'x sin k'y |

