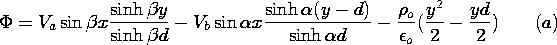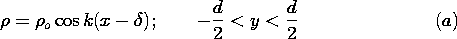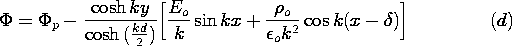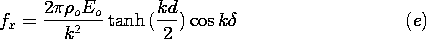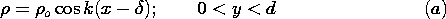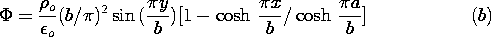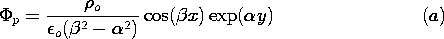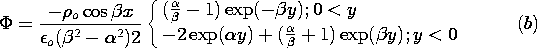5
Electroquasistatic
Fields from the
Boundary Value
Point of View
5.0 Introduction
The electroquasistatic laws were discussed in Chap. 4. The
electric field intensity E is irrotational and represented by the
negative gradient of the electric potential.
 Gauss' law is then satisfied if
the electric potential
Gauss' law is then satisfied if
the electric potential  is related to the charge density
is related to the charge density  by
Poisson's equation
by
Poisson's equation
 In charge-free regions of space,
In charge-free regions of space,  obeys Laplace's equation, (2),
with
obeys Laplace's equation, (2),
with  = 0.
= 0.
The last part of Chap. 4 was devoted to an "opportunistic"
approach to finding boundary value solutions. An exception was the
numerical scheme described in Sec. 4.8 that led to the solution of a
boundary value problem using the source-superposition approach. In
this chapter, a more direct attack is made on solving boundary value
problems without necessarily resorting to numerical methods. It is one
that will be used extensively not only as effects of polarization and
conduction are added to the EQS laws, but in dealing with MQS systems
as well.
Once again, there is an analogy useful for those familiar
with the description of linear circuit dynamics in terms of ordinary
differential equations. With time as the independent variable, the
response to a drive that is turned on when t = 0 can be determined in
two ways. The first represents the response as a superposition of
impulse responses. The resulting convolution integral represents the
response for all time, before and after t = 0 and even when t = 0.
This is the analogue of the point of view taken in the first part of
Chap. 4.
The second approach represents the history of the dynamics prior
to when t = 0 in terms of initial conditions. With the
understanding that
interest is confined to times subsequent to t = 0, the response is
then divided into "particular" and "homogeneous" parts. The
particular solution to the differential equation representing the
circuit is not unique, but insures that at each instant in the
temporal range of interest, the differential equation is satisfied.
This particular solution need not satisfy the initial conditions. In
this chapter, the "drive" is the charge density, and the particular
potential response guarantees that Poisson's equation, (2), is
satisfied everywhere in the spatial region of interest.
In the circuit analogue, the homogeneous solution is used to
satisfy the initial conditions. In the field problem, the homogeneous
solution is used to satisfy boundary conditions. In a circuit, the
homogeneous solution can be thought of as the response to drives that
occurred prior to when t = 0 (outside the temporal range of
interest). In
the determination of the potential distribution, the homogeneous
response is one predicted by Laplace's equation, (2), with
 = 0, and
can be regarded either as caused by fictitious charges residing
outside the region of interest or as caused by the surface
charges induced on the boundaries.
= 0, and
can be regarded either as caused by fictitious charges residing
outside the region of interest or as caused by the surface
charges induced on the boundaries.
The development of these ideas in Secs. 5.1-5.3 is
self-contained and does not depend on a familiarity with circuit
theory. However, for those familiar with the solution of ordinary
differential equations, it is satisfying to see that the approaches
used here for dealing with partial differential equations are a
natural extension of those used for ordinary differential equations.
Although it can often be found more simply by other methods, a
particular solution always follows from the superposition
integral. The main thrust of this chapter is therefore toward a
determination of homogeneous solutions, of finding solutions to
Laplace's equation. Many practical configurations have boundaries
that are described by setting one of the coordinate variables in a
three-dimensional coordinate system equal to a constant. For example,
a box having rectangular cross-sections has walls described by setting
one Cartesian coordinate equal to a constant to describe the boundary.
Similarly, the boundaries of a circular cylinder are naturally
described in cylindrical coordinates. So it is that there is great
interest in having solutions to Laplace's equation that naturally
"fit" these configurations. With many examples interwoven into the
discussion, much of this chapter is devoted to cataloging these
solutions. The results are used in this chapter for describing EQS
fields in free space. However, as effects of polarization and
conduction are added to the EQS purview, and as MQS systems with
magnetization and conduction are considered, the homogeneous solutions
to Laplace's equation established in this chapter will be a continual
resource.
A review of Chap. 4 will identify many solutions to Laplace's
equation. As long as the field source is outside the region of
interest, the resulting potential obeys Laplace's equation. What is
different about the solutions established in this chapter? A hint
comes from the numerical procedure used in Sec. 4.8 to satisfy
arbitrary boundary conditions. There, a superposition of N solutions
to Laplace's equation was used to satisfy conditions at N points on
the boundaries. Unfortunately, to determine the amplitudes of these N
solutions, N equations had to be solved for N unknowns.
The solutions to Laplace's equation found in this chapter can
also be used as the terms in an infinite series that is made to
satisfy arbitrary boundary conditions. But what is different about the
terms in this series is their orthogonality. This property of the
solutions makes it possible to explicitly determine the individual
amplitudes in the series. The notion of the orthogonality of functions
may already be familiar through an exposure to Fourier analysis. In
any case, the fundamental ideas involved are introduced in Sec. 5.5.
5.1 Particular and Homogeneous Solutions to Poisson'sand Laplace's Equations
Suppose we want to analyze an electroquasistatic situation as
shown in Fig. 5.1.1. A charge distribution  (r)
is specified in the
part of space of interest, designated by the volume V. This region is
bounded by perfect conductors of specified shape and location. Known
potentials are applied to these conductors and the enclosing
surface, which may be at infinity.
(r)
is specified in the
part of space of interest, designated by the volume V. This region is
bounded by perfect conductors of specified shape and location. Known
potentials are applied to these conductors and the enclosing
surface, which may be at infinity.
 In the space between the conductors, the potential function obeys
Poisson's equation, (5.0.2). A particular solution of this equation
within the prescribed volume V is given by the superposition integral,
(4.5.3).
In the space between the conductors, the potential function obeys
Poisson's equation, (5.0.2). A particular solution of this equation
within the prescribed volume V is given by the superposition integral,
(4.5.3).
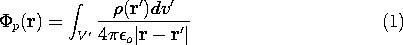 This potential obeys Poisson's equation at each point within the
volume V. Since we do not evaluate this equation outside the
volume V, the integration over the sources called for in (1) need
include no sources other than those within the volume V. This
makes it clear that the particular solution is not unique, because
the addition to the
potential made by integrating over arbitrary charges outside the
volume V will only give rise to a potential, the Laplacian derivative
of which is zero within the volume V.
This potential obeys Poisson's equation at each point within the
volume V. Since we do not evaluate this equation outside the
volume V, the integration over the sources called for in (1) need
include no sources other than those within the volume V. This
makes it clear that the particular solution is not unique, because
the addition to the
potential made by integrating over arbitrary charges outside the
volume V will only give rise to a potential, the Laplacian derivative
of which is zero within the volume V.
Is (1) the complete solution? Because it is not unique, the
answer must be, surely not. Further, it is clear that no information as
to the position and shape of the conductors is built into this
solution. Hence, the electric field obtained as the negative gradient
of the potential  p of (1) will, in general, possess a finite
tangential component on the surfaces of the electrodes. On the other
hand, the conductors have surface charge
distributions which adjust themselves so as to cause the net electric
field on the surfaces of the conductors to have vanishing tangential
electric field components. The distribution of these surface charges
is not known at the outset and hence cannot be included in the
integral (1).
p of (1) will, in general, possess a finite
tangential component on the surfaces of the electrodes. On the other
hand, the conductors have surface charge
distributions which adjust themselves so as to cause the net electric
field on the surfaces of the conductors to have vanishing tangential
electric field components. The distribution of these surface charges
is not known at the outset and hence cannot be included in the
integral (1).
A way out of this dilemma is as follows: The potential
distribution we seek within the space not occupied by the conductors
is the result of two charge distributions. First is the
prescribed volume charge distribution leading to the potential
function  p, and second is the charge distributed on the
conductor surfaces. The potential function produced by the surface
charges must obey the source-free Poisson's equation in the space V
of interest. Let us denote this solution to the homogeneous form of
Poisson's equation by the potential function
p, and second is the charge distributed on the
conductor surfaces. The potential function produced by the surface
charges must obey the source-free Poisson's equation in the space V
of interest. Let us denote this solution to the homogeneous form of
Poisson's equation by the potential function  h.
Then, in the volume V,
h.
Then, in the volume V,  h must satisfy Laplace's equation.
h must satisfy Laplace's equation.
 The superposition principle then makes it possible to write the total
potential as
The superposition principle then makes it possible to write the total
potential as
 The problem of finding the complete field distribution now
reduces to that of finding a solution such that the net
potential
The problem of finding the complete field distribution now
reduces to that of finding a solution such that the net
potential  of (3) has the prescribed potentials vi on the
surfaces Si. Now
of (3) has the prescribed potentials vi on the
surfaces Si. Now  p is known and can be evaluated on the
surface Si. Evaluation of (3) on Si gives
p is known and can be evaluated on the
surface Si. Evaluation of (3) on Si gives
 so that the homogeneous solution is prescribed on the boundaries Si.
so that the homogeneous solution is prescribed on the boundaries Si.
 Hence, the determination of an electroquasistatic field with
prescribed potentials on the boundaries is reduced to finding the
solution to Laplace's equation, (2), that satisfies the boundary
condition given by (5).
Hence, the determination of an electroquasistatic field with
prescribed potentials on the boundaries is reduced to finding the
solution to Laplace's equation, (2), that satisfies the boundary
condition given by (5).
The approach which has been formalized in this section is another
point of view applicable to the boundary value problems in the last
part of Chap. 4. Certainly, the abstract view of the boundary value
situation provided by Fig. 5.1.1 is not different from that of
Fig. 4.6.1. In Example 4.6.4, the field shown in Fig. 4.6.8 is
determined
for a point charge adjacent to an equipotential charge-neutral
spherical electrode. In the volume V of interest outside the
electrode, the volume charge distribution is singular, the point charge
q. The potential given by (4.6.35), in fact, takes the form of (3).
The particular solution can be taken as the first term, the potential of a
point charge. The second and third terms, which are equivalent to the
potentials caused by the fictitious charges within the sphere, can be
taken as the homogeneous solution.
Superposition to Satisfy Boundary Conditions
In the following sections, superposition will often be used in
another way to satisfy
boundary conditions. Suppose that there is no charge density in the
volume V, and again the potentials on each of the n surfaces Sj
are vj. Then

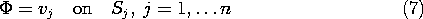 The solution is broken into a superposition of solutions
The solution is broken into a superposition of solutions  j that
meet the required condition on the j-th surface but are zero on all of
the others.
j that
meet the required condition on the j-th surface but are zero on all of
the others.

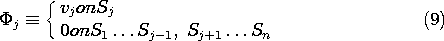 Each term is a solution to Laplace's equation, (6), so the sum is as
well.
Each term is a solution to Laplace's equation, (6), so the sum is as
well.
 In Sec. 5.5, a method is developed for satisfying arbitrary boundary
conditions on one of four surfaces enclosing a volume of interest.
In Sec. 5.5, a method is developed for satisfying arbitrary boundary
conditions on one of four surfaces enclosing a volume of interest.
Capacitance Matrix
Suppose that in the n electrode system the net charge on the i-th
electrode is to be found. In view of (8), the integral of E  da over the surface Si enclosing this electrode then gives
da over the surface Si enclosing this electrode then gives
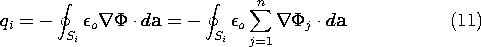 Because of the linearity of Laplace's equation, the potential
Because of the linearity of Laplace's equation, the potential  j
is proportional to the voltage exciting that potential, vj. It follows
that (11) can be written in terms of capacitance parameters that are
independent of the excitations. That is, (11) becomes
j
is proportional to the voltage exciting that potential, vj. It follows
that (11) can be written in terms of capacitance parameters that are
independent of the excitations. That is, (11) becomes
 where the capacitance coefficients are
where the capacitance coefficients are
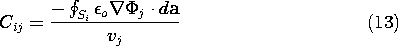 The charge on the i-th electrode is a linear superposition of the
contributions of all n voltages. The coefficient multiplying its
own voltage, Cii, is called the self-capacitance, while the
others, Cij, i \not= j, are the mutual capacitances.
The charge on the i-th electrode is a linear superposition of the
contributions of all n voltages. The coefficient multiplying its
own voltage, Cii, is called the self-capacitance, while the
others, Cij, i \not= j, are the mutual capacitances.
5.2 Uniqueness of Solutions to Poisson's Equation
We shall show in this section that a potential distribution
obeying Poisson's equation is completely specified within a volume V
if the potential is specified over the surfaces bounding that volume.
Such a uniqueness theorem is useful for two reasons: (a) It tells us
that if we have found such a solution to Poisson's equation, whether
by mathematical analysis or physical insight, then we have found the
only solution; and (b) it tells us what boundary conditions are
appropriate to uniquely specify a solution. If there is no charge
present in the volume of interest, then the theorem states the
uniqueness of solutions to Laplace's equation.
Following the method "reductio ad absurdum", we assume that the
solution is not unique- that two solutions,  a and
a and  b,
exist, satisfying the same boundary conditions- and then show that
this is impossible. The presumably different solutions
b,
exist, satisfying the same boundary conditions- and then show that
this is impossible. The presumably different solutions  a and
a and
 b must satisfy Poisson's equation with the same charge
distribution and must satisfy the same boundary conditions.
b must satisfy Poisson's equation with the same charge
distribution and must satisfy the same boundary conditions.
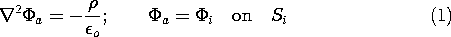
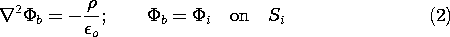 It follows that with
It follows that with  d defined as the difference in the two
potentials,
d defined as the difference in the two
potentials,  d =
d =  a -
a -  b,
b,
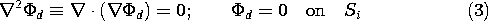 A simple argument now shows that the only way
A simple argument now shows that the only way  d can both
satisfy Laplace's equation and be zero on all of the bounding surfaces
is for it to be zero. First, it is argued that
d can both
satisfy Laplace's equation and be zero on all of the bounding surfaces
is for it to be zero. First, it is argued that  d cannot
possess a maximum or minimum at any point within V. With the help of
Fig. 5.2.1, visualize the negative of the gradient of
d cannot
possess a maximum or minimum at any point within V. With the help of
Fig. 5.2.1, visualize the negative of the gradient of  d, a
field line, as it passes through some point ro. Because the
field is solenoidal (divergence free), such a field line cannot start
or stop within V (Sec. 2.7). Further, the field defines a potential
(4.1.4). Hence, as one proceeds along the field line in the
direction of the negative gradient, the potential has to decrease
until the field line reaches one of the surfaces Si bounding V.
Similarly, in the opposite direction, the potential has to increase
until another one of the surfaces is reached. Accordingly, all
maximum and minimum values of
d, a
field line, as it passes through some point ro. Because the
field is solenoidal (divergence free), such a field line cannot start
or stop within V (Sec. 2.7). Further, the field defines a potential
(4.1.4). Hence, as one proceeds along the field line in the
direction of the negative gradient, the potential has to decrease
until the field line reaches one of the surfaces Si bounding V.
Similarly, in the opposite direction, the potential has to increase
until another one of the surfaces is reached. Accordingly, all
maximum and minimum values of  d (r ) have to be located on
the surfaces.
d (r ) have to be located on
the surfaces.
 The difference potential at any interior point cannot assume a
value larger than or smaller than the largest or smallest value of
the potential on the surfaces. But the surfaces are themselves at
zero potential. It follows that the difference potential is zero
everywhere in V and that
The difference potential at any interior point cannot assume a
value larger than or smaller than the largest or smallest value of
the potential on the surfaces. But the surfaces are themselves at
zero potential. It follows that the difference potential is zero
everywhere in V and that  a =
a =  b. Therefore, only one
solution exists
to the boundary value problem stated with (1).
b. Therefore, only one
solution exists
to the boundary value problem stated with (1).
5.3 Continuity Conditions
At the surfaces of metal conductors, charge densities accumulate that
are only a few atomic distances thick. In describing their fields,
the details of the distribution within this thin layer are often not of
interest. Thus, the charge is represented by a surface charge density
(1.3.11) and the surface supporting the charge treated as a
surface of discontinuity.
In such cases, it is often convenient to divide a volume in which
the field is to be determined into regions separated by the surfaces
of discontinuity, and to use piece-wise continuous functions to
represent the fields. Continuity conditions are then needed to
connect field solutions in two regions separated by the discontinuity.
These conditions are implied by the differential equations that apply
throughout the region. They assure that the fields are consistent
with the basic laws, even in passing through the discontinuity.
Each of the four Maxwell's equations implies a continuity condition.
Because of the singular nature of the source distribution, these laws
are used in integral form to relate the fields to either side of the
surface of discontinuity. With the vector n defined as the unit
normal to the
surface of discontinuity and pointing from region (b) to region (a),
the continuity conditions were summarized in Table 1.8.3.
In the EQS approximation, the laws of primary interest are
Faraday's law without the magnetic induction and Gauss' law, the first
two equations of Chap. 4. Thus, the corresponding EQS continuity
conditions are

 Because the magnetic induction makes no contribution to Faraday's
continuity condition in any case, these conditions are the same as for
the general electrodynamic laws. As a reminder, the contour enclosing
the integration surface over which Faraday's law was integrated (Sec.
1.6) to obtain (1) is shown in Fig. 5.3.1a. The integration volume
used to obtain (2) from Gauss' law (Sec. 1.3) is similarly shown in
Fig. 5.3.1b.
Because the magnetic induction makes no contribution to Faraday's
continuity condition in any case, these conditions are the same as for
the general electrodynamic laws. As a reminder, the contour enclosing
the integration surface over which Faraday's law was integrated (Sec.
1.6) to obtain (1) is shown in Fig. 5.3.1a. The integration volume
used to obtain (2) from Gauss' law (Sec. 1.3) is similarly shown in
Fig. 5.3.1b.
 What are the continuity conditions on the electric potential?
The potential
What are the continuity conditions on the electric potential?
The potential  is continuous across a surface of discontinuity
even if that surface carries a surface charge density. This will be
the case when the E field is finite (a dipole layer containing an
infinite field causes a jump of potential), because then the line
integral of the electric field from one side of the surface to the
other side is zero, the path-length being infinitely small.
is continuous across a surface of discontinuity
even if that surface carries a surface charge density. This will be
the case when the E field is finite (a dipole layer containing an
infinite field causes a jump of potential), because then the line
integral of the electric field from one side of the surface to the
other side is zero, the path-length being infinitely small.
 To determine the jump condition representing Gauss' law through
the surface of discontinuity, it was integrated (Sec. 1.3) over the
volume shown intersecting the surface in Fig. 5.3.1b. The resulting
continuity condition, (2), is written in terms of the potential by
recognizing that in the EQS approximation, E = -
To determine the jump condition representing Gauss' law through
the surface of discontinuity, it was integrated (Sec. 1.3) over the
volume shown intersecting the surface in Fig. 5.3.1b. The resulting
continuity condition, (2), is written in terms of the potential by
recognizing that in the EQS approximation, E = - 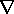
 .
.
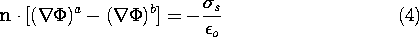 At a surface of discontinuity that carries a surface charge density,
the normal derivative of the potential is discontinuous.
At a surface of discontinuity that carries a surface charge density,
the normal derivative of the potential is discontinuous.
The continuity conditions become boundary conditions if they are
made to represent physical constraints that go beyond those already
implied by the laws that prevail in the volume. A familiar example is
one where the surface is that of an electrode constrained in its
potential. Then the continuity condition (3) requires that the
potential in the volume adjacent to the electrode be the given
potential of the electrode. This statement cannot be justified without
invoking information about the physical nature of the electrode (that
it is "infinitely conducting," for example) that is not represented
in the volume laws and hence is not intrinsic to the continuity
conditions.
5.4 Solutions to Laplace's Equation in CartesianCoordinates
Having investigated some general properties of solutions to
Poisson's equation, it is now appropriate to study specific methods of
solution to Laplace's equation subject to boundary conditions.
Exemplified by this and the next section are three standard steps
often used in representing EQS fields. First, Laplace's equation is
set up in the coordinate system in which the boundary surfaces are
coordinate surfaces. Then, the partial differential equation is
reduced to a set of ordinary differential equations by separation of
variables. In this way, an infinite set of solutions is generated.
Finally, the boundary conditions are satisfied by superimposing the
solutions found by separation of variables.
In this section, solutions are derived that are natural if
boundary conditions are stated along coordinate surfaces of a
Cartesian coordinate system. It is assumed that the fields depend on
only two coordinates, x and y, so that Laplace's equation is (Table I)
 This is a partial differential equation in two independent
variables. One time-honored method of mathematics is to reduce a new
problem to a problem previously solved. Here the process of finding
solutions to the partial differential equation is reduced to one of
finding solutions to ordinary
differential equations. This is accomplished by the method of
separation of variables. It consists of assuming solutions with the
special space dependence
This is a partial differential equation in two independent
variables. One time-honored method of mathematics is to reduce a new
problem to a problem previously solved. Here the process of finding
solutions to the partial differential equation is reduced to one of
finding solutions to ordinary
differential equations. This is accomplished by the method of
separation of variables. It consists of assuming solutions with the
special space dependence
 In (2), X is assumed to be a function of x alone and Y is a
function of y alone. If need be, a general space dependence is then
recovered by superposition of these special solutions. Substitution of
(2) into (1) and division by
In (2), X is assumed to be a function of x alone and Y is a
function of y alone. If need be, a general space dependence is then
recovered by superposition of these special solutions. Substitution of
(2) into (1) and division by  then gives
then gives
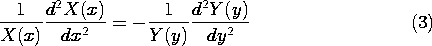 Total derivative symbols are used
because the respective functions X and Y are by definition only
functions of x and y.
Total derivative symbols are used
because the respective functions X and Y are by definition only
functions of x and y.
In (3) we now have on the left-hand side a function of x alone,
on the right-hand side a function of y alone. The equation can be
satisfied independent of x and y only if each of these expressions is
constant. We denote this "separation" constant by k2, and it
follows that
 and
and
 These equations have the solutions
These equations have the solutions
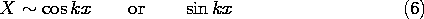
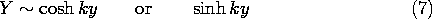 If k = 0, the solutions degenerate into
If k = 0, the solutions degenerate into
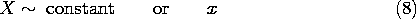
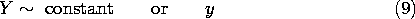 The product solutions, (2), are summarized in the first four rows of
Table 5.4.1. Those in the right-hand column are simply those of the
middle column with the roles of x and y interchanged. Generally,
we will leave the prime off the k' in writing these solutions.
Exponentials are also solutions to (7). These, sometimes more
convenient, solutions are summarized in the last four rows of the
table.
The product solutions, (2), are summarized in the first four rows of
Table 5.4.1. Those in the right-hand column are simply those of the
middle column with the roles of x and y interchanged. Generally,
we will leave the prime off the k' in writing these solutions.
Exponentials are also solutions to (7). These, sometimes more
convenient, solutions are summarized in the last four rows of the
table.
The solutions summarized in this table can be used to gain
insight into the nature of EQS fields. A good investment is
therefore made if they are now visualized.
The fields represented by the potentials in the left-hand column
of Table 5.4.1 are all familiar. Those that are linear in x and y
represent uniform fields, in the x and y directions, respectively.
The potential xy is familiar from Fig. 4.1.3. We will use similar
conventions to represent the potentials of the second column, but it
is helpful to have in mind the three-dimensional portrayal exemplified
for the potential xy in Fig. 4.1.4. In the more complicated field maps
to follow, the sketch is visualized as a contour map of the potential
 with peaks of positive potential and valleys of negative potential.
with peaks of positive potential and valleys of negative potential.
On the top and left peripheries of Fig. 5.4.1 are sketched the
functions cos kx and cosh ky, respectively, the product of which is the
first of the potentials in the middle column of Table 5.4.1. If we
start out from the origin in either the +y or -y directions (north or
south), we climb a potential hill. If we instead proceed in the +x or
-x directions (east or west), we move downhill. An easterly path
begun on the potential hill to the north of the origin corresponds to
a decrease in the cos kx factor. To follow a path of
equal elevation, the cosh ky factor must increase, and this
implies that the path must turn northward.
 A good starting point in making these field sketches is the
identification of the contours of zero potential. In the plot of the
second potential in the middle column of Table 5.4.1, shown in
Fig. 5.4.2, these are the y axis and the lines kx = +
A good starting point in making these field sketches is the
identification of the contours of zero potential. In the plot of the
second potential in the middle column of Table 5.4.1, shown in
Fig. 5.4.2, these are the y axis and the lines kx = +  /2, +
3
/2, +
3 /2, etc. The
dependence on y is now odd rather than even, as it was for the plot of
Fig. 5.4.1. Thus, the origin is now on the side of a potential hill
that slopes downward from north to south.
/2, etc. The
dependence on y is now odd rather than even, as it was for the plot of
Fig. 5.4.1. Thus, the origin is now on the side of a potential hill
that slopes downward from north to south.
 The solutions in the third and fourth rows of the second column
possess the same field patterns as those just discussed provided those
patterns are respectively shifted in the x direction. In the last
four rows of Table 5.4.1 are four additional possible solutions which
are linear combinations of the previous four in that column. Because
these decay exponentially in either the +y or -y directions, they
are useful for representing solutions in problems where an infinite
half-space is considered.
The solutions in the third and fourth rows of the second column
possess the same field patterns as those just discussed provided those
patterns are respectively shifted in the x direction. In the last
four rows of Table 5.4.1 are four additional possible solutions which
are linear combinations of the previous four in that column. Because
these decay exponentially in either the +y or -y directions, they
are useful for representing solutions in problems where an infinite
half-space is considered.
The solutions in Table 5.4.1 are nonsingular throughout the
entire x-y plane. This means that Laplace's equation is obeyed
everywhere within the finite x-y plane, and hence the field lines are
continuous; they do not appear or disappear. The sketches show that
the fields become stronger and stronger as one proceeds in the
positive and negative y directions. The lines of electric field
originate on positive charges and terminate on negative charges at y
 \pm
\pm 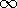 .
Thus, for the plots shown in Figs. 5.4.1 and 5.4.2, the charge
distributions at infinity must consist of alternating distributions of
positive and negative charges of infinite amplitude.
.
Thus, for the plots shown in Figs. 5.4.1 and 5.4.2, the charge
distributions at infinity must consist of alternating distributions of
positive and negative charges of infinite amplitude.
Two final observations serve to further develop an appreciation
for the nature of solutions to Laplace's equation. First, the
third dimension can be used to represent the potential in the manner
of Fig. 4.1.4, so that the potential surface has the shape of a
membrane stretched from boundaries that are elevated in proportion
to their potentials.
Laplace's equation, (1), requires that the sum of quantities
that reflect the curvatures in the x and y directions vanish. If the
second derivative of a function is positive, it is curved upward; and
if it is negative, it is curved downward. If the curvature is positive
in the x direction, it must be negative in the y direction. Thus, at
the origin in Fig. 5.4.1, the potential is cupped downward for
excursions in the x direction, and so it must be cupped upward for
variations in the y direction. A similar deduction must apply at every
point in the x-y plane.
Second, because the k that appears in the periodic functions of
the second column in Table 5.4.1 is the same as that in the exponential
and hyperbolic functions, it is clear that the more rapid the periodic
variation, the more rapid is the decay or apparent growth.

5.5 Modal Expansion to Satisfy Boundary Conditions
Each of the solutions obtained in the preceding section by
separation of variables could be produced by an appropriate potential
applied to pairs of parallel surfaces in the planes x = constant and
y = constant. Consider, for example, the fourth solution in the column
k2 \geq 0 of Table 5.4.1, which with a constant multiplier is

 This solution has
This solution has  = 0 in the plane y = 0 and in the planes x
= n
= 0 in the plane y = 0 and in the planes x
= n /k, where n is an integer. Suppose that we set k = n
/k, where n is an integer. Suppose that we set k = n /a so that
/a so that  = 0 in the plane y = a as well. Then at y =
b, the potential of (1)
= 0 in the plane y = a as well. Then at y =
b, the potential of (1)
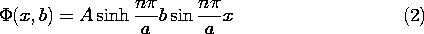 has a sinusoidal dependence on x. If a potential of the form of
(2) were applied along the surface at y = b, and the surfaces at x
= 0, x = a, and y = 0 were held at zero potential (by, say,
planar conductors
held at zero potential), then the potential, (1), would exist within
the space 0 < x < a, 0 < y < b.
Segmented electrodes having each segment
constrained to the appropriate potential could be used to approximate
the distribution at y = b. The potential and field plots for n = 1
and n = 2
are given in Fig. 5.5.1. Note that the theorem of Sec. 5.2 insures
that the specified potential is unique.
has a sinusoidal dependence on x. If a potential of the form of
(2) were applied along the surface at y = b, and the surfaces at x
= 0, x = a, and y = 0 were held at zero potential (by, say,
planar conductors
held at zero potential), then the potential, (1), would exist within
the space 0 < x < a, 0 < y < b.
Segmented electrodes having each segment
constrained to the appropriate potential could be used to approximate
the distribution at y = b. The potential and field plots for n = 1
and n = 2
are given in Fig. 5.5.1. Note that the theorem of Sec. 5.2 insures
that the specified potential is unique.
But what can be done to describe the field if the wall potentials
are not constrained to fit neatly the solution obtained by separation
of variables? For example, suppose that the fields are desired in the
same region of rectangular cross-section, but with an electrode at y
= b
constrained to have a potential v that is independent of x. The
configuration is now as shown in Fig. 5.5.2.
 A line of attack is suggested by the infinite number of
solutions, having the form of (1), that meet the boundary condition
on three of the four walls. The superposition principle makes it clear
that any linear combination of these is also a solution, so if we let
An be arbitrary coefficients, a more general solution is
A line of attack is suggested by the infinite number of
solutions, having the form of (1), that meet the boundary condition
on three of the four walls. The superposition principle makes it clear
that any linear combination of these is also a solution, so if we let
An be arbitrary coefficients, a more general solution is
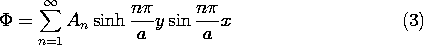 Note that k has
been assigned values such that the sine function is zero in the planes
x = 0 and x = a.
Now how can we adjust the coefficients so that the
boundary condition at the driven electrode, at y = b, is met? One
approach that we will not have to use is suggested by the numerical
method described in Sec. 4.8. The electrode could be divided into N
segments and (3) evaluated at the center point of each of the
segments. If the infinite series were truncated at N terms, the
result would be N equations that were linear in the N unknowns An.
This system of equations could be inverted to determine the An's.
Substitution of these into (3) would then comprise a solution to the
boundary value problem. Unfortunately, to achieve reasonable
accuracy, large values of N would be required and a computer would be
needed.
Note that k has
been assigned values such that the sine function is zero in the planes
x = 0 and x = a.
Now how can we adjust the coefficients so that the
boundary condition at the driven electrode, at y = b, is met? One
approach that we will not have to use is suggested by the numerical
method described in Sec. 4.8. The electrode could be divided into N
segments and (3) evaluated at the center point of each of the
segments. If the infinite series were truncated at N terms, the
result would be N equations that were linear in the N unknowns An.
This system of equations could be inverted to determine the An's.
Substitution of these into (3) would then comprise a solution to the
boundary value problem. Unfortunately, to achieve reasonable
accuracy, large values of N would be required and a computer would be
needed.
The power of the approach of variable separation is that it
results in solutions that are orthogonal in a sense that makes it
possible to determine explicitly the coefficients An.
The evaluation of the coefficients is remarkably simple. First,
(3) is evaluated on the surface of the electrode where the potential
is known.
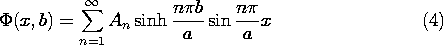 On
the right is the infinite series of sinusoidal functions with
coefficients that are to be determined. On the left is a given
function of x. We multiply both sides of the expression by sin
(m
On
the right is the infinite series of sinusoidal functions with
coefficients that are to be determined. On the left is a given
function of x. We multiply both sides of the expression by sin
(m x/a), where m is one integer, and then both sides of the
expression are integrated over the width of the system.
x/a), where m is one integer, and then both sides of the
expression are integrated over the width of the system.
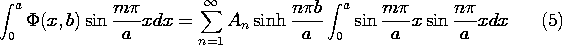 The functions sin (n
The functions sin (n x/a) and sin (m
x/a) and sin (m x/a) are orthogonal
in the sense that the integral of their product over the specified
interval is zero, unless m = n.
x/a) are orthogonal
in the sense that the integral of their product over the specified
interval is zero, unless m = n.
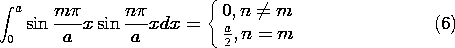 Thus, all the terms on the right in (5) vanish, except the one having
n = m. Of course, m can be any integer, so we can solve (5) for
the m-th amplitude and then replace m by n.
Thus, all the terms on the right in (5) vanish, except the one having
n = m. Of course, m can be any integer, so we can solve (5) for
the m-th amplitude and then replace m by n.
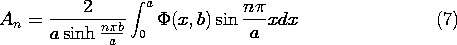 Given any
distribution of potential on the surface y = b, this integral can be
carried out and hence the coefficients determined. In this specific
problem, the potential is v at each point on the electrode surface.
Thus, (7) is evaluated to give
Given any
distribution of potential on the surface y = b, this integral can be
carried out and hence the coefficients determined. In this specific
problem, the potential is v at each point on the electrode surface.
Thus, (7) is evaluated to give
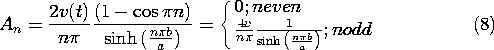 Finally, substitution of these coefficients into
(3) gives the desired potential.
Finally, substitution of these coefficients into
(3) gives the desired potential.
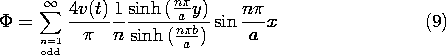 Each product term in this
infinite series satisfies Laplace's equation and the zero potential
condition on three of the surfaces enclosing the region of interest.
The sum satisfies the potential condition on the "last" boundary.
Note that the sum is not itself in the form of the product of a
function of x alone and a function of y alone.
Each product term in this
infinite series satisfies Laplace's equation and the zero potential
condition on three of the surfaces enclosing the region of interest.
The sum satisfies the potential condition on the "last" boundary.
Note that the sum is not itself in the form of the product of a
function of x alone and a function of y alone.
The modal expansion is applicable with an arbitrary distribution
of potential on the "last" boundary. But what if we have an arbitrary
distribution of potential on all four of the planes enclosing the
region of interest? The superposition principle justifies using the
sum of four solutions of the type illustrated here. Added to the
series solution already found are three more, each analogous to the
previous one, but rotated by 90 degrees. Because each of the four
series has a finite potential only on the part of the boundary to
which its series applies, the sum of the four satisfy all boundary
conditions.
The potential given by (9) is illustrated in Fig. 5.5.3. In
the three-dimensional portrayal, it is especially clear that the field
is infinitely large in the corners where the driven electrode meets
the grounded walls. Where the electric field emanates from the driven
electrode, there is surface charge, so at the corners there is an
infinite surface charge density. In practice, of course, the spacing
is not infinitesimal and the fields are not infinite.

Demonstration 5.5.1. Capacitance Attenuator
Because neither of the field laws in this chapter involve time
derivatives, the field that has been determined is correct for v =
v(t),
an arbitrary function of time. As a consequence, the coefficients
An are also functions of time. Thus, the charges induced on the
walls of the box are time varying, as can be seen if the wall at y = 0
is isolated from the grounded side walls and connected to ground
through a resistor. The configuration is shown in cross-section by
Fig. 5.5.4. The resistance R is small enough so that the potential
vo is small compared with v.
 The charge induced on this output electrode is found by applying
Gauss' integral law with an integration surface enclosing the
electrode. The width of the electrode in the z direction is w, so
The charge induced on this output electrode is found by applying
Gauss' integral law with an integration surface enclosing the
electrode. The width of the electrode in the z direction is w, so
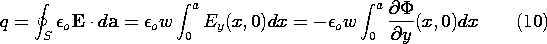 This expression is evaluated using (9).
This expression is evaluated using (9).
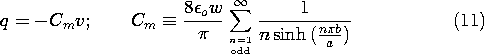 Conservation of charge requires
that the current through the resistance be the rate of change of
this charge with respect to time. Thus, the output voltage is
Conservation of charge requires
that the current through the resistance be the rate of change of
this charge with respect to time. Thus, the output voltage is
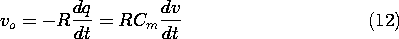 and if v = V sin
and if v = V sin 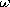 t, then
t, then
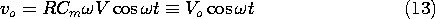 The experiment shown in Fig. 5.5.5 is designed to
demonstrate the dependence of the output voltage on the spacing b
between the input and output electrodes. It follows from (13) and
(11) that this voltage can be written in normalized form as
The experiment shown in Fig. 5.5.5 is designed to
demonstrate the dependence of the output voltage on the spacing b
between the input and output electrodes. It follows from (13) and
(11) that this voltage can be written in normalized form as
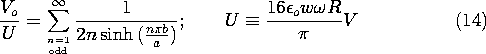
 Thus, the
natural log of the normalized voltage has the dependence on the
electrode spacing shown in Fig. 5.5.5. Note that
with increasing b/a the function quickly becomes a straight line. In
the limit of large b/a, the hyperbolic sine can be approximated by
\exp (n
Thus, the
natural log of the normalized voltage has the dependence on the
electrode spacing shown in Fig. 5.5.5. Note that
with increasing b/a the function quickly becomes a straight line. In
the limit of large b/a, the hyperbolic sine can be approximated by
\exp (n b/a)/2 and the series can be approximated by one term. Thus,
the dependence of the output voltage on the electrode spacing becomes
simply
b/a)/2 and the series can be approximated by one term. Thus,
the dependence of the output voltage on the electrode spacing becomes
simply
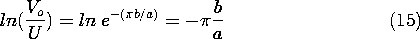 and so the asymptotic slope of the curve is -
and so the asymptotic slope of the curve is - .
.
Charges induced on the input electrode have their images either
on the side walls of the box or on the output electrode. If b/a is
small, almost all of these images are on the output electrode, but as
it is withdrawn, more and more of the images are on the side walls and
fewer are on the output electrode.
In retrospect, there are several matters that deserve further
discussion. First, the potential used as a starting point in this
section, (1), is one from a list of four in Table 5.4.1. What type
of procedure can be used to select the appropriate form? In general,
the solution used to satisfy the zero potential boundary condition on
the "first" three surfaces is a linear combination of the four
possible solutions. Thus, with the A's denoting undetermined
coefficients, the general form of the solution is
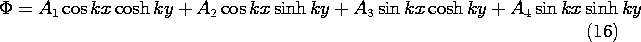 Formally, (1) was selected by eliminating three of these four
coefficients. The first two must vanish because the function must be
zero at x = 0. The third is excluded because the potential must be
zero at y = 0. Thus, we are led to the last term, which, if A4 =
A, is (1).
The methodical elimination of solutions is necessary.
Because the origin of the coordinates is arbitrary, setting up a
simple expression for the potential is a matter
of choosing the origin of coordinates properly so that as many of the
solutions (16) are eliminated as possible. We purposely choose the
origin so that a single term from the four in (16) meets the boundary
condition at x = 0 and y = 0. The selection of product solutions
from the list should interplay with the choice of coordinates. Some
combinations are much more convenient than others. This will be
exemplified in this and the following chapters.
Formally, (1) was selected by eliminating three of these four
coefficients. The first two must vanish because the function must be
zero at x = 0. The third is excluded because the potential must be
zero at y = 0. Thus, we are led to the last term, which, if A4 =
A, is (1).
The methodical elimination of solutions is necessary.
Because the origin of the coordinates is arbitrary, setting up a
simple expression for the potential is a matter
of choosing the origin of coordinates properly so that as many of the
solutions (16) are eliminated as possible. We purposely choose the
origin so that a single term from the four in (16) meets the boundary
condition at x = 0 and y = 0. The selection of product solutions
from the list should interplay with the choice of coordinates. Some
combinations are much more convenient than others. This will be
exemplified in this and the following chapters.
The remainder of this section is devoted to a more detailed
discussion of the expansion in sinusoids represented by (9). In the
plane y = b, the potential distribution is of the form
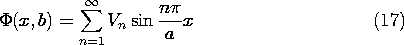 where the procedure for determining the coefficients has led to (8),
written here in terms of the coefficients Vn of (17) as
where the procedure for determining the coefficients has led to (8),
written here in terms of the coefficients Vn of (17) as
 The approximation to the
potential v that is uniform over the span of the driving electrode is
shown in Fig. 5.5.6. Equation (17) represents a square wave of period
2a extending over all x, -
The approximation to the
potential v that is uniform over the span of the driving electrode is
shown in Fig. 5.5.6. Equation (17) represents a square wave of period
2a extending over all x, - < x < +\infty.
One half of a period appears
as shown in the figure. It is possible to represent this distribution
in terms of sinusoids alone because it is odd in x. In general, a
periodic function is represented by a Fourier series of both sines and
cosines. In the present problem, cosines were missing because the
potential had to be zero at x = 0 and x = a. Study of a Fourier
series shows that the series converges to the actual function in the
sense that in the limit of an infinite number of terms,
< x < +\infty.
One half of a period appears
as shown in the figure. It is possible to represent this distribution
in terms of sinusoids alone because it is odd in x. In general, a
periodic function is represented by a Fourier series of both sines and
cosines. In the present problem, cosines were missing because the
potential had to be zero at x = 0 and x = a. Study of a Fourier
series shows that the series converges to the actual function in the
sense that in the limit of an infinite number of terms,
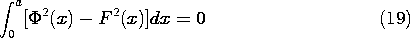 where
where  (x) is the actual potential distribution
and F(x) is the Fourier series approximation.
(x) is the actual potential distribution
and F(x) is the Fourier series approximation.
 To see the generality of the approach exemplified here, we show
that the orthogonality property of the functions X(x) results from the
differential equation and boundary conditions. Thus, it should not be
surprising that the solutions in other coordinate systems also have
an orthogonality property.
To see the generality of the approach exemplified here, we show
that the orthogonality property of the functions X(x) results from the
differential equation and boundary conditions. Thus, it should not be
surprising that the solutions in other coordinate systems also have
an orthogonality property.
In all cases, the orthogonality property is associated with any
one of the factors in a product solution. For the Cartesian problem
considered here, it is X(x) that satisfies boundary conditions at two
points in space. This is assured by adjusting the eigenvalue kn =
n /a so that the eigenfunction or mode, sin (n
/a so that the eigenfunction or mode, sin (n x/a), is zero
at x = 0 and x = a. This function satisfies (5.4.4) and the
boundary conditions.
x/a), is zero
at x = 0 and x = a. This function satisfies (5.4.4) and the
boundary conditions.
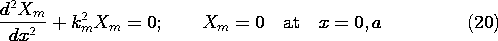 The subscript m is used to recognize that there is an infinite number
of solutions to this problem. Another solution, say the n-th, must
also satisfy this equation and the boundary conditions.
The subscript m is used to recognize that there is an infinite number
of solutions to this problem. Another solution, say the n-th, must
also satisfy this equation and the boundary conditions.
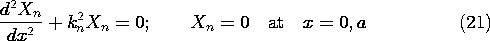 The
orthogonality property for these modes, exploited in evaluating the
coefficients of the series expansion, is
The
orthogonality property for these modes, exploited in evaluating the
coefficients of the series expansion, is
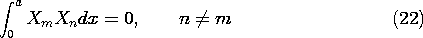 To prove this condition in
general, we multiply (20) by Xn and integrate between the points
where the boundary conditions apply.
To prove this condition in
general, we multiply (20) by Xn and integrate between the points
where the boundary conditions apply.
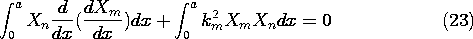 By identifying u = Xn and v = dXm/dx, the first term is
integrated by parts to obtain
By identifying u = Xn and v = dXm/dx, the first term is
integrated by parts to obtain
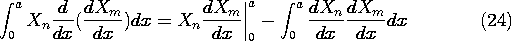 The first term
on the right vanishes because of the boundary conditions. Thus, (23)
becomes
The first term
on the right vanishes because of the boundary conditions. Thus, (23)
becomes
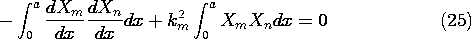 If these same steps are completed with n and m interchanged, the
result is
(25) with n and m interchanged. Because the first term in (25) is
the same as its counterpart in this second equation, subtraction of
the two expressions yields
If these same steps are completed with n and m interchanged, the
result is
(25) with n and m interchanged. Because the first term in (25) is
the same as its counterpart in this second equation, subtraction of
the two expressions yields
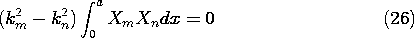 Thus, the functions are orthogonal provided that kn \not= km. For
this specific problem, the eigenfunctions are Xn = sin (n
Thus, the functions are orthogonal provided that kn \not= km. For
this specific problem, the eigenfunctions are Xn = sin (n /a) and
the eigenvalues are kn = n
/a) and
the eigenvalues are kn = n /a.
But in general we can expect that our product
solutions to Laplace's equation in other coordinate systems will result
in a set of functions having similar orthogonality properties.
/a.
But in general we can expect that our product
solutions to Laplace's equation in other coordinate systems will result
in a set of functions having similar orthogonality properties.
5.6 Solutions to Poisson's Equation with BoundaryConditions
An approach to solving Poisson's equation in a region bounded by
surfaces of known potential was outlined in Sec. 5.1. The potential
was divided into a particular part, the Laplacian of which balances
- /
/ o
throughout the region of interest, and a homogeneous part that
makes the sum of the two potentials satisfy the boundary conditions.
In short,
o
throughout the region of interest, and a homogeneous part that
makes the sum of the two potentials satisfy the boundary conditions.
In short,


 and on the enclosing surfaces,
and on the enclosing surfaces,
 The following examples illustrate this approach. At the same
time they demonstrate the use of the Cartesian coordinate solutions to
Laplace's equation and the idea that the fields described can be
time varying.
The following examples illustrate this approach. At the same
time they demonstrate the use of the Cartesian coordinate solutions to
Laplace's equation and the idea that the fields described can be
time varying.
Example 5.6.1. Field of Traveling Wave of Space Charge
between Equipotential Surfaces
The cross-section of a two-dimensional system that stretches to
infinity in the x and z directions is shown in Fig. 5.6.1. Conductors
in the planes y = a and y = -a bound the region of interest. Between
these planes the charge density is periodic in the x direction and
uniformly distributed in the y direction.

 The parameters
The parameters  o and
o and  are given constants. For now,
the segment
connected to ground through the resistor in the lower electrode can be
regarded as being at the same zero potential as the remainder of the
electrode in the plane x = -a and the electrode in the plane y = a.
First we ask for the field distribution.
are given constants. For now,
the segment
connected to ground through the resistor in the lower electrode can be
regarded as being at the same zero potential as the remainder of the
electrode in the plane x = -a and the electrode in the plane y = a.
First we ask for the field distribution.
Remember that any particular solution to (2) will do. Because
the charge density is independent of y, it is natural to look for a
particular solution with the same property. Then, on the left
in (2) is a second derivative with respect to x, and the equation
can be integrated twice to obtain
 This particular solution is independent of y. Note that it is not
the potential that would be obtained by evaluating the superposition
integral over the charge between the grounded planes. Viewed over all
space, that charge distribution is not independent of y. In fact, the
potential of (6) is associated with a charge distribution as given
by (5) that extends to infinity in the +y and -y directions.
This particular solution is independent of y. Note that it is not
the potential that would be obtained by evaluating the superposition
integral over the charge between the grounded planes. Viewed over all
space, that charge distribution is not independent of y. In fact, the
potential of (6) is associated with a charge distribution as given
by (5) that extends to infinity in the +y and -y directions.
The homogeneous solution must make up for the fact that (6)
does not satisfy the boundary conditions. That is, at the boundaries,
 = 0 in (1), so the homogeneous and particular solutions must
balance there.
= 0 in (1), so the homogeneous and particular solutions must
balance there.
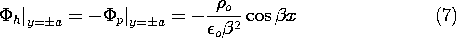 Thus, we are looking for a solution to Laplace's equation, (3),
that satisfies these boundary conditions. Because the potential has
the same value on the boundaries, and the origin of the y axis has
been chosen to be midway between, it is clear that the potential must
be an even function of y. Further, it must have a periodicity in the
x direction that matches that of (7). Thus, from the list of
solutions to Laplace's equation in Cartesian coordinates in the
middle column of Table 5.4.1, k =
Thus, we are looking for a solution to Laplace's equation, (3),
that satisfies these boundary conditions. Because the potential has
the same value on the boundaries, and the origin of the y axis has
been chosen to be midway between, it is clear that the potential must
be an even function of y. Further, it must have a periodicity in the
x direction that matches that of (7). Thus, from the list of
solutions to Laplace's equation in Cartesian coordinates in the
middle column of Table 5.4.1, k =  , the sin kx terms
are eliminated in
favor of the cos kx solutions, and the cosh ky solution is selected
because it is even in y.
, the sin kx terms
are eliminated in
favor of the cos kx solutions, and the cosh ky solution is selected
because it is even in y.
 The coefficient A is now adjusted so that the boundary conditions are
satisfied by substituting (8) into (7).
The coefficient A is now adjusted so that the boundary conditions are
satisfied by substituting (8) into (7).
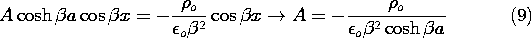 Superposition of the particular solution, (7), and the
homogeneous solution given by substituting the coefficient of (9)
into (8), results in the desired potential distribution.
Superposition of the particular solution, (7), and the
homogeneous solution given by substituting the coefficient of (9)
into (8), results in the desired potential distribution.
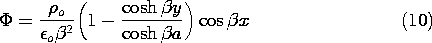 The mathematical solutions used in deriving (10) are illustrated
in Fig. 5.6.2. The particular solution describes an electric field
that originates in regions of positive charge density and terminates
in regions of negative charge density. It is purely x directed and
is therefore tangential to the equipotential boundary. The
homogeneous solution that is added to this field is entirely due to
surface charges. These give rise to a field that bucks out the
tangential field at the walls, rendering them surfaces of constant
potential. Thus, the sum of the solutions (also shown in the figure),
satisfies Gauss' law and the boundary conditions.
The mathematical solutions used in deriving (10) are illustrated
in Fig. 5.6.2. The particular solution describes an electric field
that originates in regions of positive charge density and terminates
in regions of negative charge density. It is purely x directed and
is therefore tangential to the equipotential boundary. The
homogeneous solution that is added to this field is entirely due to
surface charges. These give rise to a field that bucks out the
tangential field at the walls, rendering them surfaces of constant
potential. Thus, the sum of the solutions (also shown in the figure),
satisfies Gauss' law and the boundary conditions.
 With this static view of the fields firmly in mind, suppose that
the charge distribution is moving in the x direction with the
velocity v.
With this static view of the fields firmly in mind, suppose that
the charge distribution is moving in the x direction with the
velocity v.
 The variable x in (5) has been replaced by x - vt. With this moving
charge distribution, the field also moves. Thus, (10) becomes
The variable x in (5) has been replaced by x - vt. With this moving
charge distribution, the field also moves. Thus, (10) becomes
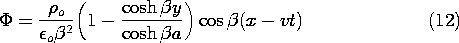 Note that the homogeneous solution is now a linear combination of the
first and third solutions in the middle column of Table 5.4.1.
Note that the homogeneous solution is now a linear combination of the
first and third solutions in the middle column of Table 5.4.1.
As the space charge wave moves by, the charges induced on the
perfectly conducting walls follow along in synchronism. The current
that accompanies the redistribution of surface charges is detected if
a section of the wall is insulated from the rest and connected to
ground through a resistor, as shown in Fig. 5.6.1. Under the
assumption that the resistance is small enough so that the segment
remains at essentially zero potential, what is the output voltage vo?
The current through the resistor is found by invoking charge
conservation for the segment to find the current that is the time
rate of change of the net charge on the segment. The latter follows
from Gauss' integral law and (12) as
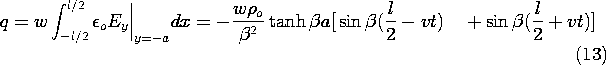 It follows that the dynamics of the traveling wave of space charge is
reflected in a measured voltage of
It follows that the dynamics of the traveling wave of space charge is
reflected in a measured voltage of
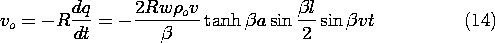 In writing this expression, the double-angle formulas have been
invoked.
Several predictions should be consistent with intuition. The
output voltage varies sinusoidally with time at a frequency that is
proportional to the velocity and inversely proportional to the
wavelength, 2
In writing this expression, the double-angle formulas have been
invoked.
Several predictions should be consistent with intuition. The
output voltage varies sinusoidally with time at a frequency that is
proportional to the velocity and inversely proportional to the
wavelength, 2 /
/ . The higher the velocity, the greater the
voltage. Finally, if the detection electrode is a multiple of the
wavelength 2
. The higher the velocity, the greater the
voltage. Finally, if the detection electrode is a multiple of the
wavelength 2 /
/ , the voltage is zero.
, the voltage is zero.
If the charge density is concentrated in surface-like regions
that are thin compared to other dimensions of interest, it is possible
to solve Poisson's equation with boundary conditions using a procedure
that has the appearance of solving Laplace's equation rather than
Poisson's equation. The potential is typically broken into piece-wise
continuous functions, and the effect of the charge density is brought in
by Gauss' continuity condition, which is used to splice the functions
at the surface occupied by the charge density. The following example
illustrates this procedure. What is accomplished is a solution to
Poisson's equation in the entire region, including the charge-carrying
surface.
Example 5.6.2. Thin Bunched Charged-Particle Beam
between Conducting Plates
In microwave amplifiers and oscillators of the electron beam
type, a basic problem is the evaluation of the electric field produced
by a bunched electron beam. The cross-section of the beam is usually
small compared with a free space wavelength of an electromagnetic
wave, in which case the electroquasistatic approximation applies.
We consider a strip electron beam having a charge density that is
uniform over its cross-section 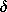 . The beam moves with
the velocity v in the x direction between two planar perfect
conductors situated at y = \pm a
and held at zero potential. The configuration is shown in
cross-section in Fig. 5.6.3. In addition to the uniform charge
density, there is a "ripple" of charge density, so that the net charge
density is
. The beam moves with
the velocity v in the x direction between two planar perfect
conductors situated at y = \pm a
and held at zero potential. The configuration is shown in
cross-section in Fig. 5.6.3. In addition to the uniform charge
density, there is a "ripple" of charge density, so that the net charge
density is
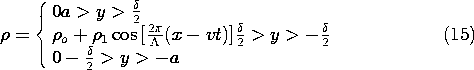 where
where  o,
o,  1, and \Lambda are constants. The system can
be idealized to be of infinite extent in the x and y directions.
1, and \Lambda are constants. The system can
be idealized to be of infinite extent in the x and y directions.
 The thickness
The thickness 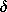 of the beam is much smaller than the wavelength
of the periodic charge density ripple, and much smaller than the
spacing 2a of the planar conductors. Thus, the beam is treated as a
sheet of surface charge with a density
of the beam is much smaller than the wavelength
of the periodic charge density ripple, and much smaller than the
spacing 2a of the planar conductors. Thus, the beam is treated as a
sheet of surface charge with a density
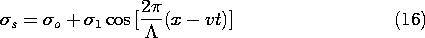 where
where  o =
o =  o
o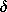 and
and  1 =
1 =  1
1 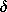 .
.
In regions (a) and (b), respectively, above and below the beam, the
potential obeys Laplace's equation. Superscripts (a) and (b) are now
used to designate variables evaluated in these regions. To guarantee
that the fundamental laws are satisfied within the sheet, these
potentials must satisfy the jump conditions implied by the laws of
Faraday and Gauss, (5.3.4) and (5.3.5). That is, at y = 0

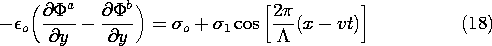 To complete the specification of the field in the region between the
plates, boundary conditions are, at y = a,
To complete the specification of the field in the region between the
plates, boundary conditions are, at y = a,
 and at y = -a,
and at y = -a,
 In the respective regions, the potential is split into dc and ac
parts, respectively, produced by the uniform and ripple parts of the
charge density.
In the respective regions, the potential is split into dc and ac
parts, respectively, produced by the uniform and ripple parts of the
charge density.
 By definition,
By definition,  o and
o and  1 satisfy Laplace's equation and
(17), (19), and (20). The dc part,
1 satisfy Laplace's equation and
(17), (19), and (20). The dc part,  o, satisfies (18) with only
the first term on the right, while the ac part,
o, satisfies (18) with only
the first term on the right, while the ac part,  1, satisfies
(18) with only the second term.
1, satisfies
(18) with only the second term.
The dc surface charge density is independent of x, so it is
natural to look for potentials that are also independent of x. From
the first column in Table 5.4.1, such solutions are

 The four coefficients in these expressions are determined from
(17)-(20), if need be, by substitution of these expressions and formal
solution for the coefficients. More attractive is the solution by
inspection that recognizes that the system is symmetric
with respect to y, that the uniform surface charge gives rise to
uniform electric fields that are directed upward and downward in the
two regions, and that the associated linear potential must be zero at
the two boundaries.
The four coefficients in these expressions are determined from
(17)-(20), if need be, by substitution of these expressions and formal
solution for the coefficients. More attractive is the solution by
inspection that recognizes that the system is symmetric
with respect to y, that the uniform surface charge gives rise to
uniform electric fields that are directed upward and downward in the
two regions, and that the associated linear potential must be zero at
the two boundaries.

 Now consider the ac part of the potential. The x dependence is
suggested by (18), which makes it clear that for product
solutions, the x dependence of the potential must be
the cosine function moving with time. Neither the sinh nor the cosh
functions vanish at the
boundaries, so we will have to take a linear combination
of these to satisfy the boundary conditions at y = +a. This is
effectively done by inspection if it is recognized that the origin of
the y axis used in writing the solutions is arbitrary.
The solutions to Laplace's equation that satisfy the boundary
conditions, (19) and (20), are
Now consider the ac part of the potential. The x dependence is
suggested by (18), which makes it clear that for product
solutions, the x dependence of the potential must be
the cosine function moving with time. Neither the sinh nor the cosh
functions vanish at the
boundaries, so we will have to take a linear combination
of these to satisfy the boundary conditions at y = +a. This is
effectively done by inspection if it is recognized that the origin of
the y axis used in writing the solutions is arbitrary.
The solutions to Laplace's equation that satisfy the boundary
conditions, (19) and (20), are
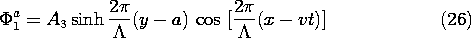
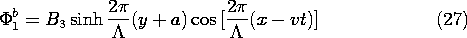 These potentials must match at y = 0, as required by (17), so we
might just as well have written them with the coefficients adjusted
accordingly.
These potentials must match at y = 0, as required by (17), so we
might just as well have written them with the coefficients adjusted
accordingly.
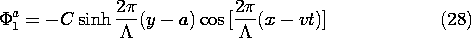
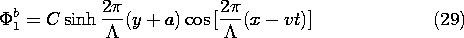 The one remaining coefficient is determined by substituting these
expressions into (18) (with
The one remaining coefficient is determined by substituting these
expressions into (18) (with  o omitted).
o omitted).
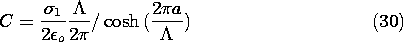 We have found the potential as a piece-wise continuous function. In
region (a), it is the superposition of (24) and (28),
while in region (b), it is (25) and (29). In both expressions, C is
provided by (30).
We have found the potential as a piece-wise continuous function. In
region (a), it is the superposition of (24) and (28),
while in region (b), it is (25) and (29). In both expressions, C is
provided by (30).
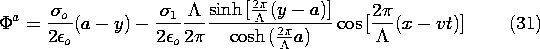
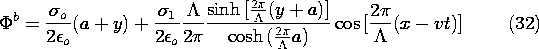 When t = 0, the ac part of this potential distribution is as shown
by Fig. 5.6.4. With increasing time, the field distribution
translates to the right with the velocity v. Note that some lines of
electric field intensity that originate on the beam terminate
elsewhere on the beam, while others terminate on the equipotential
walls. If the walls are even a wavelength away from the beam (a =
\Lambda ), almost all the field lines terminate elsewhere on the
beam. That is, coupling to the wall is significant only if the
wavelength is on the order of or larger than a. The nature of
solutions to Laplace's equation is in evidence. Two-dimensional
potentials that vary rapidly in one direction must decay equally
rapidly in a perpendicular direction.
When t = 0, the ac part of this potential distribution is as shown
by Fig. 5.6.4. With increasing time, the field distribution
translates to the right with the velocity v. Note that some lines of
electric field intensity that originate on the beam terminate
elsewhere on the beam, while others terminate on the equipotential
walls. If the walls are even a wavelength away from the beam (a =
\Lambda ), almost all the field lines terminate elsewhere on the
beam. That is, coupling to the wall is significant only if the
wavelength is on the order of or larger than a. The nature of
solutions to Laplace's equation is in evidence. Two-dimensional
potentials that vary rapidly in one direction must decay equally
rapidly in a perpendicular direction.
 A comparison of the fields from the sheet beam shown in Fig. 5.6.4
and the periodic distribution of volume charge density shown in
Fig. 5.6.2 is a reminder of the similarity of the two physical
situations. Even though Laplace's equation applies in the subregions
of the configuration considered in this section, it is really
Poisson's equation that is solved "in the large," as in the previous
example.
A comparison of the fields from the sheet beam shown in Fig. 5.6.4
and the periodic distribution of volume charge density shown in
Fig. 5.6.2 is a reminder of the similarity of the two physical
situations. Even though Laplace's equation applies in the subregions
of the configuration considered in this section, it is really
Poisson's equation that is solved "in the large," as in the previous
example.
5.7 Solutions to Laplace's Equation in Polar Coordinates
In electroquasistatic field problems in which the boundary
conditions are specified on circular cylinders or on planes of
constant  , it is convenient to match these conditions with solutions
to Laplace's equation in polar coordinates (cylindrical coordinates
with no z dependence). The approach adopted is entirely analogous to
the one used in Sec. 5.4 in the case of Cartesian coordinates.
, it is convenient to match these conditions with solutions
to Laplace's equation in polar coordinates (cylindrical coordinates
with no z dependence). The approach adopted is entirely analogous to
the one used in Sec. 5.4 in the case of Cartesian coordinates.
 As a reminder, the polar coordinates are defined in Fig. 5.7.1.
In these coordinates and with the understanding that there is no z
dependence, Laplace's equation, Table I, (8), is
As a reminder, the polar coordinates are defined in Fig. 5.7.1.
In these coordinates and with the understanding that there is no z
dependence, Laplace's equation, Table I, (8), is
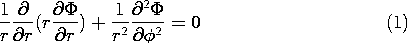 One difference between this equation and Laplace's equation written in
Cartesian coordinates is immediately apparent: In polar coordinates,
the equation contains coefficients which not only depend on the
independent variable r but become singular at the origin. This
singular behavior of the differential equation will affect the type of
solutions we now obtain.
One difference between this equation and Laplace's equation written in
Cartesian coordinates is immediately apparent: In polar coordinates,
the equation contains coefficients which not only depend on the
independent variable r but become singular at the origin. This
singular behavior of the differential equation will affect the type of
solutions we now obtain.
In order to reduce the solution of the partial differential
equation to the simpler problem of solving total differential
equations, we look for solutions which can be written as products of
functions of r alone and of  alone.
alone.
 When this assumed form of
When this assumed form of  is introduced into (1), and the result
divided by
is introduced into (1), and the result
divided by  and multiplied by r, we obtain
and multiplied by r, we obtain
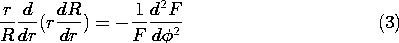 We find on the left-hand side of (3) a function of r alone and on
the right-hand side a function of
We find on the left-hand side of (3) a function of r alone and on
the right-hand side a function of  alone. The two sides of the
equation can balance if and only if the function of
alone. The two sides of the
equation can balance if and only if the function of  and the function
of r are both equal to the same constant. For this "separation
constant" we introduce the symbol -m2.
and the function
of r are both equal to the same constant. For this "separation
constant" we introduce the symbol -m2.

 For m2 > 0, the solutions to the differential equation for F are
conveniently written as
For m2 > 0, the solutions to the differential equation for F are
conveniently written as
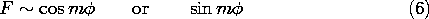 Because of the space-varying coefficients, the solutions to (5) are
not exponentials or linear combinations of exponentials as has so far
been the case. Fortunately, the solutions are nevertheless simple.
Substitution of a solution having the form rn into (5) shows that
the equation is satisfied provided that n = \pm m. Thus,
Because of the space-varying coefficients, the solutions to (5) are
not exponentials or linear combinations of exponentials as has so far
been the case. Fortunately, the solutions are nevertheless simple.
Substitution of a solution having the form rn into (5) shows that
the equation is satisfied provided that n = \pm m. Thus,
 In the special case of a zero separation constant, the limiting
solutions are
In the special case of a zero separation constant, the limiting
solutions are
 and
and
 The product solutions shown in the first two columns of Table 5.7.1,
constructed by taking all possible combinations of these solutions,
are those most often used in polar coordinates. But what are the
solutions if m2 < 0?
In Cartesian coordinates, changing the sign of the separation
constant k2 amounts to interchanging the roles of the x and y
coordinates. Solutions that are periodic in the x direction become
exponential in character, while the exponential decay and growth in the
y direction becomes periodic. Here the geometry is such that the r
and
The product solutions shown in the first two columns of Table 5.7.1,
constructed by taking all possible combinations of these solutions,
are those most often used in polar coordinates. But what are the
solutions if m2 < 0?
In Cartesian coordinates, changing the sign of the separation
constant k2 amounts to interchanging the roles of the x and y
coordinates. Solutions that are periodic in the x direction become
exponential in character, while the exponential decay and growth in the
y direction becomes periodic. Here the geometry is such that the r
and  coordinates are not interchangeable, but the new solutions
resulting from replacing m2 by -p2, where p is a real number,
essentially make the oscillating dependence radial instead of
azimuthal, and the exponential dependence azimuthal rather than radial.
To see this, let m2 = -p2, or m = jp, and the solutions given
by (7) become
coordinates are not interchangeable, but the new solutions
resulting from replacing m2 by -p2, where p is a real number,
essentially make the oscillating dependence radial instead of
azimuthal, and the exponential dependence azimuthal rather than radial.
To see this, let m2 = -p2, or m = jp, and the solutions given
by (7) become
 These take a more familiar appearance if it is recognized that r can
be written identically as
These take a more familiar appearance if it is recognized that r can
be written identically as
 Introduction of this identity into (10) then gives the more familiar
complex exponential, which can be split into its real and imaginary
parts using Euler's formula.
Introduction of this identity into (10) then gives the more familiar
complex exponential, which can be split into its real and imaginary
parts using Euler's formula.
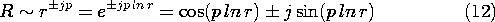 Thus, two independent solutions for R(r) are the cosine and sine
functions of p ln r. The
Thus, two independent solutions for R(r) are the cosine and sine
functions of p ln r. The  dependence is now either
represented by \exp \pm p
dependence is now either
represented by \exp \pm p or the hyperbolic functions that are
linear combinations of these exponentials. These solutions are
summarized in the right-hand column of Table 5.7.1.
In principle, the solution to a given problem can be approached
by the methodical elimination of solutions from the catalogue given in
Table 5.7.1. In fact, most problems are best approached by
attributing to each solution some physical meaning. This makes it
possible to define coordinates so that the field representation is
kept as simple as possible. With that objective, consider first the
solutions appearing in the first column of Table 5.7.1.
or the hyperbolic functions that are
linear combinations of these exponentials. These solutions are
summarized in the right-hand column of Table 5.7.1.
In principle, the solution to a given problem can be approached
by the methodical elimination of solutions from the catalogue given in
Table 5.7.1. In fact, most problems are best approached by
attributing to each solution some physical meaning. This makes it
possible to define coordinates so that the field representation is
kept as simple as possible. With that objective, consider first the
solutions appearing in the first column of Table 5.7.1.
The constant potential is an obvious solution and need not be
considered further. We have a solution in row two for which the
potential is proportional to the angle. The equipotential lines and
the field lines are illustrated in Fig. 5.7.2a. Evaluation of the
field by taking the gradient of the potential in polar coordinates
(the gradient operator given in Table I) shows that it becomes
infinitely large as the origin is reached. The potential increases
from zero to 2 as the angle
as the angle  is increased from zero to
2
is increased from zero to
2 . If the potential is to be single valued, then we cannot allow
that
. If the potential is to be single valued, then we cannot allow
that  increase
further without leaving the region of validity of the solution. This
observation identifies the solution with a physical field observed when
two semi-infinite conducting plates are held at different potentials
and the distance between the conducting plates at their junction is
assumed to be negligible. In this case, shown in Fig. 5.7.2, the
outside field between the plates is properly represented by a
potential proportional to
increase
further without leaving the region of validity of the solution. This
observation identifies the solution with a physical field observed when
two semi-infinite conducting plates are held at different potentials
and the distance between the conducting plates at their junction is
assumed to be negligible. In this case, shown in Fig. 5.7.2, the
outside field between the plates is properly represented by a
potential proportional to  .
.
With the plates separated by an angle of 90 degrees rather than
360 degrees, the potential that is proportional to  is seen in the
corners of the configuration shown in Fig. 5.5.3.
The m2 = 0 solution in the third row is familiar from Sec. 1.3, for
it is the potential of a line charge. The fourth m2 = 0 solution is
sketched in Fig. 5.7.3.
In order to sketch the potentials corresponding to the solutions
in the second column of Table 5.7.1, the separation constant must be
specified. For the time being, let us assume that m is an integer.
For m = 1, the solutions r cos
is seen in the
corners of the configuration shown in Fig. 5.5.3.
The m2 = 0 solution in the third row is familiar from Sec. 1.3, for
it is the potential of a line charge. The fourth m2 = 0 solution is
sketched in Fig. 5.7.3.
In order to sketch the potentials corresponding to the solutions
in the second column of Table 5.7.1, the separation constant must be
specified. For the time being, let us assume that m is an integer.
For m = 1, the solutions r cos  and r sin
and r sin  represent
familiar potentials. Observe that the polar coordinates are related
to the Cartesian ones defined in Fig. 5.7.1 by
represent
familiar potentials. Observe that the polar coordinates are related
to the Cartesian ones defined in Fig. 5.7.1 by


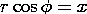
 The fields that go with these potentials are best found by taking the
gradient in Cartesian coordinates. This makes it clear that they can
be used to represent uniform fields having the x and y
directions, respectively. To emphasize the simplicity of these
solutions, which are made complicated by the polar representation, the
second function of (13) is shown in Fig. 5.7.4a.
The fields that go with these potentials are best found by taking the
gradient in Cartesian coordinates. This makes it clear that they can
be used to represent uniform fields having the x and y
directions, respectively. To emphasize the simplicity of these
solutions, which are made complicated by the polar representation, the
second function of (13) is shown in Fig. 5.7.4a.
 Figure 5.7.4b shows the potential r-1 sin
Figure 5.7.4b shows the potential r-1 sin  . To stay on a
contour of constant potential in the first quadrant of this figure as
. To stay on a
contour of constant potential in the first quadrant of this figure as
 is increased toward
is increased toward  /2, it is necessary to first increase
r, and then as
the sine function decreases in the second quadrant, to decrease r.
The potential is singular at the origin of r; as the origin is
approached from above, it is large and positive; while from below it is
large and negative. Thus, the field lines emerge from the origin
within 0 <
/2, it is necessary to first increase
r, and then as
the sine function decreases in the second quadrant, to decrease r.
The potential is singular at the origin of r; as the origin is
approached from above, it is large and positive; while from below it is
large and negative. Thus, the field lines emerge from the origin
within 0 <  <
<  and converge toward the origin in the lower
half-plane. There must be a source at the origin composed of equal
and opposite charges on the two sides of the plane r sin
and converge toward the origin in the lower
half-plane. There must be a source at the origin composed of equal
and opposite charges on the two sides of the plane r sin  = 0.
The source, which is uniform and of infinite extent in the
z direction, is a line dipole.
= 0.
The source, which is uniform and of infinite extent in the
z direction, is a line dipole.
This conclusion is confirmed by direct evaluation of the
potential produced by two line charges, the charge
-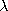 l situated at the origin, the charge
+
l situated at the origin, the charge
+ l at a very small distance away from the
origin at r = d,
l at a very small distance away from the
origin at r = d,  =
=  /2. The potential follows from
steps paralleling
those used for the three-dimensional dipole in Sec. 4.4.
/2. The potential follows from
steps paralleling
those used for the three-dimensional dipole in Sec. 4.4.
 The spatial dependence of the potential is indeed sin
The spatial dependence of the potential is indeed sin  /r. In
an analogy with the three-dimensional dipole of Sec. 4.4, p
/r. In
an analogy with the three-dimensional dipole of Sec. 4.4, p \equiv
\equiv 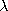 l d is defined as the line dipole moment. In Example
4.6.3, it is shown that the equipotentials for parallel line charges
are circular cylinders. Because this result is independent of
spacing between the line charges, it is no surprise that the
equipotentials of Fig. 5.7.4b are circular.
In summary, the m = 1 solutions can be thought of as the fields of
dipoles at infinity and at the origin. For the sine dependencies, the
dipoles are y directed, while for the cosine dependencies they are x
directed.
l d is defined as the line dipole moment. In Example
4.6.3, it is shown that the equipotentials for parallel line charges
are circular cylinders. Because this result is independent of
spacing between the line charges, it is no surprise that the
equipotentials of Fig. 5.7.4b are circular.
In summary, the m = 1 solutions can be thought of as the fields of
dipoles at infinity and at the origin. For the sine dependencies, the
dipoles are y directed, while for the cosine dependencies they are x
directed.
The solution of Fig. 5.7.5a,  \propto r2 sin 2
\propto r2 sin 2 , has
been met before in Cartesian coordinates. Either from a comparison of
the equipotential plots or by direct transformation of the Cartesian
coordinates into polar coordinates, the potential is recognized as
xy.
, has
been met before in Cartesian coordinates. Either from a comparison of
the equipotential plots or by direct transformation of the Cartesian
coordinates into polar coordinates, the potential is recognized as
xy.
 The m = 2 solution that is singular at the origin is shown in
Fig. 5.7.5b. Field lines emerge from the origin and
return to it twice as
The m = 2 solution that is singular at the origin is shown in
Fig. 5.7.5b. Field lines emerge from the origin and
return to it twice as  ranges from 0 to 2
ranges from 0 to 2 . This
observation identifies four line
charges of equal magnitude, alternating in sign as the source of the
field. Thus, the m = 2 solutions can be regarded as those of
quadrupoles at infinity and at the origin.
. This
observation identifies four line
charges of equal magnitude, alternating in sign as the source of the
field. Thus, the m = 2 solutions can be regarded as those of
quadrupoles at infinity and at the origin.
It is perhaps a bit surprising that we have obtained from
Laplace's equation solutions that are singular at the origin and hence
associated with sources at the origin. The singularity of one of the
two independent solutions to (5) can be traced to the singularity in
the coefficients of this differential equation.
From the foregoing, it is seen that increasing m introduces a
more rapid variation of the field with respect to the angular
coordinate. In problems
where the region of interest includes all values of  , m must be an
integer to make the field return to the same value after one
revolution. But, m does not have to be an integer. If the region
of interest is pie shaped, m can be
selected so that the potential passes through one cycle over an
arbitrary interval of
, m must be an
integer to make the field return to the same value after one
revolution. But, m does not have to be an integer. If the region
of interest is pie shaped, m can be
selected so that the potential passes through one cycle over an
arbitrary interval of  . For example, the periodicity angle can be
made
. For example, the periodicity angle can be
made  o by making m
o by making m o = n
o = n or m = n
or m = n /
/ o,
where n can have any integer value.
o,
where n can have any integer value.
 The solutions for m2 < 0, the right-hand column of Table 5.7.1, are
illustrated in Fig. 5.7.6 using as an example essentially the fourth
solution. Note that the radial phase has been shifted by subtracting
p ln (b) from the argument of the sine. Thus, the potential shown is
The solutions for m2 < 0, the right-hand column of Table 5.7.1, are
illustrated in Fig. 5.7.6 using as an example essentially the fourth
solution. Note that the radial phase has been shifted by subtracting
p ln (b) from the argument of the sine. Thus, the potential shown is
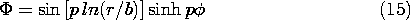 and it automatically passes through zero at the radius r = b. The
distances between radii of zero potential are not equal.
Nevertheless, the potential distribution is qualitatively similar to
that in Cartesian coordinates shown in Fig. 5.4.2. The exponential
dependence is azimuthal; that direction is thus analogous to
y in Fig. 5.4.2. In essence, the potentials for m2 < 0 are
similar to
those in Cartesian coordinates but wrapped around the z axis.
and it automatically passes through zero at the radius r = b. The
distances between radii of zero potential are not equal.
Nevertheless, the potential distribution is qualitatively similar to
that in Cartesian coordinates shown in Fig. 5.4.2. The exponential
dependence is azimuthal; that direction is thus analogous to
y in Fig. 5.4.2. In essence, the potentials for m2 < 0 are
similar to
those in Cartesian coordinates but wrapped around the z axis.

5.8 Examples in Polar Coordinates
With the objective of attaching physical insight to the polar
coordinate solutions to Laplace's equation, two types of examples are
of interest. First are certain classic problems
that have simple solutions. Second are examples that require
the generally applicable modal approach that makes it possible to
satisfy arbitrary boundary conditions.
The equipotential cylinder in a uniform applied electric field
considered in the first example is in the first category. While
an important addition to our resource of case studies, the example is
also of practical value because it allows estimates to be made in
complex engineering systems, perhaps of the degree to which an applied
field will tend to concentrate on a cylindrical object.
 In the most general problem in the second category, arbitrary
potentials are imposed on the polar coordinate boundaries enclosing a
region V, as shown in Fig. 5.8.1. The potential is the superposition
of four solutions, each meeting the potential constraint on one of the
boundaries while being zero on the other three. In Cartesian
coordinates, the approach used to find one of these four solutions,
the modal approach of Sec. 5.5, applies directly to the other three.
That is, in writing the solutions, the roles of x and y can be
interchanged. On the other hand, in polar coordinates the set of
solutions needed to represent a potential imposed on the boundaries at
r = a or r = b is different from that appropriate for potential
constraints on the boundaries at
In the most general problem in the second category, arbitrary
potentials are imposed on the polar coordinate boundaries enclosing a
region V, as shown in Fig. 5.8.1. The potential is the superposition
of four solutions, each meeting the potential constraint on one of the
boundaries while being zero on the other three. In Cartesian
coordinates, the approach used to find one of these four solutions,
the modal approach of Sec. 5.5, applies directly to the other three.
That is, in writing the solutions, the roles of x and y can be
interchanged. On the other hand, in polar coordinates the set of
solutions needed to represent a potential imposed on the boundaries at
r = a or r = b is different from that appropriate for potential
constraints on the boundaries at  = 0 or
= 0 or  =
=  o.
Examples 5.8.2 and
5.8.3 illustrate the two types of solutions needed to determine the
fields in the most general case. In the second of these, the potential
is expanded in a set of orthogonal functions that are not sines or
cosines. This gives the opportunity to form an appreciation for an
orthogonality property of the product solutions to Laplace's equation
that prevails in many other coordinate systems.
o.
Examples 5.8.2 and
5.8.3 illustrate the two types of solutions needed to determine the
fields in the most general case. In the second of these, the potential
is expanded in a set of orthogonal functions that are not sines or
cosines. This gives the opportunity to form an appreciation for an
orthogonality property of the product solutions to Laplace's equation
that prevails in many other coordinate systems.
Simple Solutions
The example considered now is the first in a series
of "cylinder" case studies built on the same m = 1 solutions. In the
next chapter, the cylinder will become a polarizable dielectric. In
Chap. 7, it will have finite conductivity and provide the basis for
establishing just how "perfect" a conductor must be to justify the
equipotential model used here. In Chaps. 8-10, the field will be
magnetic and the cylinder first perfectly conducting, then
magnetizable, and finally a shell of finite conductivity. Because of
the simplicity of the dipole solutions used in this series of
examples, in each case it is possible to focus on the physics
without becoming distracted by mathematical details.
Example 5.8.1. Equipotential Cylinder in a Uniform Electric Field
A uniform electric field Ea is applied in a direction
perpendicular to the axis of a (perfectly) conducting cylinder. Thus,
the surface of the conductor, which is at r = R, is an equipotential.
The objective is to determine the field distribution as modified by
the presence of the cylinder.
Because the boundary condition is stated on a circular
cylindrical surface, it is natural to use polar coordinates. The
field excitation comes from "infinity," where the field is known to be
uniform, of magnitude Ea, and x directed. Because our solution must
approach this uniform field far from the cylinder, it is important to
recognize at the outset that its potential, which in Cartesian
coordinates is -Ea x, is
 To this must be added the potential produced by the charges induced
on the surface of the conductor so that the surface is maintained an
equipotential. Because the solutions have to hold over the entire
range 0 <
To this must be added the potential produced by the charges induced
on the surface of the conductor so that the surface is maintained an
equipotential. Because the solutions have to hold over the entire
range 0 <  < 2
< 2 , only integer values of the separation
constant m are allowed, i.e., only solutions that are periodic in
, only integer values of the separation
constant m are allowed, i.e., only solutions that are periodic in
 . If we are to add
a function to (1) that makes the potential zero at r = R, it must
cancel the value given by (1) at each point on the surface of the
cylinder. There are two solutions in Table 5.7.1 that have the same
cos
. If we are to add
a function to (1) that makes the potential zero at r = R, it must
cancel the value given by (1) at each point on the surface of the
cylinder. There are two solutions in Table 5.7.1 that have the same
cos  dependence as (1). We pick the 1/r dependence because it
decays to zero as r
dependence as (1). We pick the 1/r dependence because it
decays to zero as r 
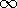 and hence does not disturb
the potential at
infinity already given by (1). With A an arbitrary coefficient, the
solution is therefore
and hence does not disturb
the potential at
infinity already given by (1). With A an arbitrary coefficient, the
solution is therefore
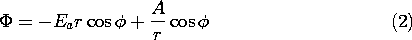 Because
Because  = 0 at r = R, evaluation of this expression shows
that the boundary condition is satisfied at every angle
= 0 at r = R, evaluation of this expression shows
that the boundary condition is satisfied at every angle  if
if
 and the potential is therefore
and the potential is therefore
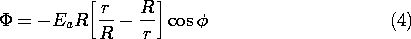 The equipotentials given by this expression are shown in Fig. 5.8.2.
Note that the x = 0 plane has been taken as having zero potential
by omitting an additive constant in (1). The field lines shown in
this figure follow from taking the gradient of (4).
The equipotentials given by this expression are shown in Fig. 5.8.2.
Note that the x = 0 plane has been taken as having zero potential
by omitting an additive constant in (1). The field lines shown in
this figure follow from taking the gradient of (4).

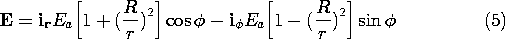 Field lines tend to concentrate on the surface where
Field lines tend to concentrate on the surface where  = 0 and
= 0 and
 =
=  . At
these locations, the field is maximum and twice the applied field. Now
that the boundary value problem has been solved, the surface charge on
the cylindrical conductor follows from Gauss' jump condition,
(5.3.2), and the fact that there is no field inside the cylinder.
. At
these locations, the field is maximum and twice the applied field. Now
that the boundary value problem has been solved, the surface charge on
the cylindrical conductor follows from Gauss' jump condition,
(5.3.2), and the fact that there is no field inside the cylinder.
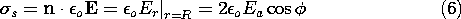 In retrospect, the boundary condition on the circular cylindrical
surface has been satisfied by adding to the uniform potential that of
an x directed line dipole. Its moment is that necessary to create a
field that cancels the tangential field on the surface caused by the
imposed field.
In retrospect, the boundary condition on the circular cylindrical
surface has been satisfied by adding to the uniform potential that of
an x directed line dipole. Its moment is that necessary to create a
field that cancels the tangential field on the surface caused by the
imposed field.
Azimuthal Modes
The preceding example considered a situation in which
Laplace's equation is obeyed in the entire range 0 <  < 2
< 2 .
The next two examples illustrate how the polar coordinate solutions
are adapted to meeting conditions on polar coordinate boundaries
that have arbitrary locations as pictured in Fig. 5.8.1.
.
The next two examples illustrate how the polar coordinate solutions
are adapted to meeting conditions on polar coordinate boundaries
that have arbitrary locations as pictured in Fig. 5.8.1.
Example 5.8.2. Modal Analysis in  : Fields in and
around Corners
: Fields in and
around Corners
The configuration shown in Fig. 5.8.3, where the potential is
zero on the walls of the region V at r = b and at  = 0 and
= 0 and
 =
=  o, but is v
on a curved electrode at r = a, is the polar coordinate analogue of that
considered in Sec. 5.5. What solutions from Table 5.7.1 are pertinent?
The region within which Laplace's equation is to be obeyed does not
occupy a full circle, and hence there is no requirement that the
potential be a single-valued function of
o, but is v
on a curved electrode at r = a, is the polar coordinate analogue of that
considered in Sec. 5.5. What solutions from Table 5.7.1 are pertinent?
The region within which Laplace's equation is to be obeyed does not
occupy a full circle, and hence there is no requirement that the
potential be a single-valued function of  . The separation
constant m can assume noninteger values.
. The separation
constant m can assume noninteger values.
 We shall attempt to satisfy the boundary conditions on the three
zero-potential boundaries using individual solutions from Table 5.7.1.
Because the potential is zero at
We shall attempt to satisfy the boundary conditions on the three
zero-potential boundaries using individual solutions from Table 5.7.1.
Because the potential is zero at  = 0, the cosine and
ln(r) terms are eliminated. The requirement that the potential
also be zero at
= 0, the cosine and
ln(r) terms are eliminated. The requirement that the potential
also be zero at  =
=  o
eliminates the functions
o
eliminates the functions  and
and  ln(r). Moreover, the
fact that the remaining sine functions must be zero at
ln(r). Moreover, the
fact that the remaining sine functions must be zero at  =
=
 o tells us that m
o tells us that m o = n
o = n .
Solutions in the last column are not appropriate because they do not
pass through zero more than once as a function of
.
Solutions in the last column are not appropriate because they do not
pass through zero more than once as a function of  . Thus,
we are led
to the two solutions in the second column that are proportional to
sin (n
. Thus,
we are led
to the two solutions in the second column that are proportional to
sin (n
 /
/ o).
o).
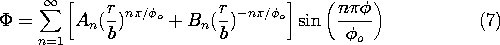 In writing these solutions, the r's have been normalized to b,
because it is then clear by inspection how the coefficients An and
Bn are related to make the potential zero at r = b, An = -Bn.
In writing these solutions, the r's have been normalized to b,
because it is then clear by inspection how the coefficients An and
Bn are related to make the potential zero at r = b, An = -Bn.
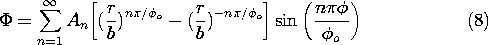 Each term in this infinite series satisfies the conditions on the
three boundaries that are constrained to zero potential. All of the
terms are now used to meet the condition at the "last" boundary, where
r = a. There we must represent a potential which jumps abruptly from
zero to v at
Each term in this infinite series satisfies the conditions on the
three boundaries that are constrained to zero potential. All of the
terms are now used to meet the condition at the "last" boundary, where
r = a. There we must represent a potential which jumps abruptly from
zero to v at  = 0, stays at the same v up to
= 0, stays at the same v up to  =
=
 o, and then jumps abruptly from v back to zero. The
determination of the coefficients in (8) that make the series of sine
functions meet this boundary condition is the same as for (5.5.4) in
the Cartesian analogue considered in Sec. 5.5. The parameter n
o, and then jumps abruptly from v back to zero. The
determination of the coefficients in (8) that make the series of sine
functions meet this boundary condition is the same as for (5.5.4) in
the Cartesian analogue considered in Sec. 5.5. The parameter n (x/a) of Sec. 5.5 is now to be identified with n
(x/a) of Sec. 5.5 is now to be identified with n (
( /
/ o). With the potential given by (8) evaluated at r = a, the
coefficients must be as in (5.5.17) and (5.5.18). Thus, to meet the
"last" boundary condition, (8) becomes the desired potential
distribution.
o). With the potential given by (8) evaluated at r = a, the
coefficients must be as in (5.5.17) and (5.5.18). Thus, to meet the
"last" boundary condition, (8) becomes the desired potential
distribution.
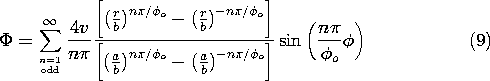 The distribution of potential and field intensity implied by this
result is much like that for the region of rectangular cross-section
depicted in Fig. 5.5.3. See Fig. 5.8.3.
The distribution of potential and field intensity implied by this
result is much like that for the region of rectangular cross-section
depicted in Fig. 5.5.3. See Fig. 5.8.3.
In the limit where b  0, the potential given by (9) becomes
0, the potential given by (9) becomes
 and describes the configurations shown in Fig. 5.8.4. Although the
wedge-shaped region is a reasonable "distortion" of its Cartesian
analogue, the field in a region with an outside corner (
and describes the configurations shown in Fig. 5.8.4. Although the
wedge-shaped region is a reasonable "distortion" of its Cartesian
analogue, the field in a region with an outside corner ( /
/ o
< 1) is also represented by (10). As long
as the leading term has the exponent
o
< 1) is also represented by (10). As long
as the leading term has the exponent  /
/ o > 1, the leading
term in the gradient [with the exponent (
o > 1, the leading
term in the gradient [with the exponent ( /
/ o) - 1]
approaches zero at the origin.
This means that the field in a wedge with
o) - 1]
approaches zero at the origin.
This means that the field in a wedge with  o <
o <  approaches
zero at its apex. However, if
approaches
zero at its apex. However, if  /
/ o < 1, which is true for
o < 1, which is true for  <
<  o < 2
o < 2 as illustrated in Fig. 5.8.4b, the leading term in
the gradient of
as illustrated in Fig. 5.8.4b, the leading term in
the gradient of  has the exponent (
has the exponent ( /
/ o) - 1 < 0, and
hence the field approaches infinity as r
o) - 1 < 0, and
hence the field approaches infinity as r 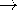 0. We conclude
that the field in the neighborhood of a sharp edge is infinite. This
observation teaches a lesson for the design of conductor shapes so as
to avoid electrical breakdown. Avoid sharp edges!
0. We conclude
that the field in the neighborhood of a sharp edge is infinite. This
observation teaches a lesson for the design of conductor shapes so as
to avoid electrical breakdown. Avoid sharp edges!

Radial Modes
The modes illustrated so far possessed sinusoidal  dependencies, and hence their superposition has taken the form of a
Fourier series. To satisfy boundary conditions imposed on constant
dependencies, and hence their superposition has taken the form of a
Fourier series. To satisfy boundary conditions imposed on constant
 planes, it is again necessary to have an infinite set of
solutions to Laplace's equation. These illustrate how the product
solutions to Laplace's equation can be used to provide orthogonal
modes that are not Fourier series.
planes, it is again necessary to have an infinite set of
solutions to Laplace's equation. These illustrate how the product
solutions to Laplace's equation can be used to provide orthogonal
modes that are not Fourier series.
To satisfy zero potential boundary conditions at r = b and r = a, it
is necessary that the function pass through zero at least twice. This
makes it clear that the solutions must be chosen from the last column
in Table 5.7.1. The functions that are proportional to the sine and
cosine functions can just as well be proportional to the sine function
shifted in phase (a linear combination of the sine and cosine). This
phase shift is adjusted to make the function zero where r = b, so that
the radial dependence is expressed as
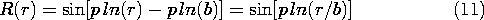 and the function made to be zero at r = a by setting
and the function made to be zero at r = a by setting
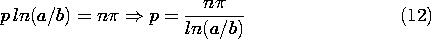 where n is an integer.
where n is an integer.
The solutions that have now been defined can be superimposed to form
a series analogous to the Fourier series.
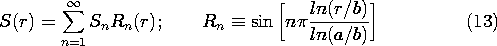 For a/b = 2, the first three terms in the series are illustrated in
Fig. 5.8.5. They have similarity to sinusoids but reflect the polar
geometry by having peaks and zero crossings skewed toward low values
of r.
For a/b = 2, the first three terms in the series are illustrated in
Fig. 5.8.5. They have similarity to sinusoids but reflect the polar
geometry by having peaks and zero crossings skewed toward low values
of r.
 With a weighting function g(r) = r-1, these modes are orthogonal
in the sense that
With a weighting function g(r) = r-1, these modes are orthogonal
in the sense that
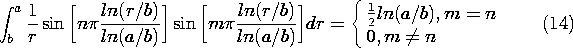 It can be shown from the differential equation defining R(r),
(5.7.5), and the boundary conditions, that the integration gives zero if
the integration is over the product of different modes. The proof is
analogous to that given in Cartesian coordinates in Sec. 5.5.
It can be shown from the differential equation defining R(r),
(5.7.5), and the boundary conditions, that the integration gives zero if
the integration is over the product of different modes. The proof is
analogous to that given in Cartesian coordinates in Sec. 5.5.
Consider now an example in which these modes are used to satisfy
a specific boundary condition.
Example 5.8.3. Modal Analysis in r
The region of interest is of the same shape as in the previous
example. However, as shown in Fig. 5.8.6, the zero potential boundary
conditions are at r = a and r = b and at  = 0. The "last"
boundary is now at
= 0. The "last"
boundary is now at  =
=  o, where an electrode connected to a
voltage source imposes a uniform potential v.
o, where an electrode connected to a
voltage source imposes a uniform potential v.
 The radial boundary conditions are satisfied by using the
functions described by (13) for the radial dependence. Because the
potential is zero where
The radial boundary conditions are satisfied by using the
functions described by (13) for the radial dependence. Because the
potential is zero where  = 0, it is then convenient to use the
hyperbolic sine to represent the
= 0, it is then convenient to use the
hyperbolic sine to represent the  dependence. Thus, from the
solutions in the last column of Table 5.7.1, we take a linear
combination of the second and fourth.
dependence. Thus, from the
solutions in the last column of Table 5.7.1, we take a linear
combination of the second and fourth.
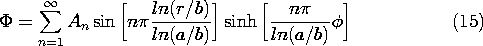 Using an approach that is analogous to that for evaluating the Fourier
coefficients in Sec. 5.5, we now use (15) on the "last"
boundary, where
Using an approach that is analogous to that for evaluating the Fourier
coefficients in Sec. 5.5, we now use (15) on the "last"
boundary, where  =
=  o and
o and  = v, multiply both sides by
the mode Rm defined with (13) and by the weighting factor 1/r, and
integrate over the radial span of the region.
= v, multiply both sides by
the mode Rm defined with (13) and by the weighting factor 1/r, and
integrate over the radial span of the region.
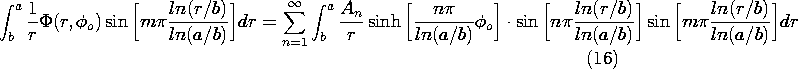 Out of the infinite series on the right, the orthogonality condition,
(14), picks only the m-th term. Thus, the equation can be solved
for Am and m
Out of the infinite series on the right, the orthogonality condition,
(14), picks only the m-th term. Thus, the equation can be solved
for Am and m  n. With the substitution u = m
n. With the substitution u = m ln(r/b)/ln(a/b), the integrals can be carried out in closed form.
ln(r/b)/ln(a/b), the integrals can be carried out in closed form.
 A picture of the potential and field intensity distributions
represented by (15) and its negative gradient is visualized by
"bending" the rectangular region shown by Fig. 5.5.3
into the curved region of Fig. 5.8.6. The role of y is now played by
A picture of the potential and field intensity distributions
represented by (15) and its negative gradient is visualized by
"bending" the rectangular region shown by Fig. 5.5.3
into the curved region of Fig. 5.8.6. The role of y is now played by
 .
.
5.9 Three Solutions to Laplace's Equation inSpherical Coordinates
The method employed to solve Laplace's equation in Cartesian
coordinates can be repeated to solve the same equation in the
spherical coordinates of Fig. 5.9.1. We have so far considered
solutions that depend on only two independent variables. In spherical
coordinates, these are commonly r and  . These two-dimensional
solutions therefore satisfy boundary conditions
on spheres and cones.
. These two-dimensional
solutions therefore satisfy boundary conditions
on spheres and cones.
 Rather than embark on an exploration of product solutions in
spherical coordinates, attention is directed in this section to three
such solutions to Laplace's equation that are already
familiar and that are remarkably useful. These will be used to
explore physical processes ranging from polarization and charge
relaxation dynamics to the induction of magnetization and eddy
currents.
Under the assumption that there is no
Rather than embark on an exploration of product solutions in
spherical coordinates, attention is directed in this section to three
such solutions to Laplace's equation that are already
familiar and that are remarkably useful. These will be used to
explore physical processes ranging from polarization and charge
relaxation dynamics to the induction of magnetization and eddy
currents.
Under the assumption that there is no  dependence, Laplace's
equation in spherical coordinates is (Table I)
dependence, Laplace's
equation in spherical coordinates is (Table I)
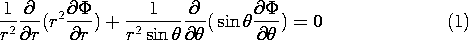 The first of the three solutions to this equation is independent
of
The first of the three solutions to this equation is independent
of  and is the potential of a point charge.
and is the potential of a point charge.
 If there is any doubt, substitution shows that Laplace's equation
is indeed satisfied. Of course, it is not satisfied at the origin
where the point charge is located.
If there is any doubt, substitution shows that Laplace's equation
is indeed satisfied. Of course, it is not satisfied at the origin
where the point charge is located.
Another of the solutions found before is the three-dimensional
dipole, (4.4.10).
 This solution factors into a function of r alone and of
This solution factors into a function of r alone and of  alone, and
hence would have to turn up in developing the product
solutions to Laplace's equation in spherical coordinates.
Substitution shows that it too is a solution of (1).
alone, and
hence would have to turn up in developing the product
solutions to Laplace's equation in spherical coordinates.
Substitution shows that it too is a solution of (1).
The third solution represents a uniform z-directed electric field
in spherical coordinates. Such a field has a potential that is linear
in z, and in spherical coordinates, z = r cos  . Thus,
the potential is
. Thus,
the potential is
 These last two solutions, for the three-dimensional dipole at the
origin and a field due to \pm charges at z
These last two solutions, for the three-dimensional dipole at the
origin and a field due to \pm charges at z  \pm
\pm  ,
are similar to those for
dipoles in two dimensions, the m = 1 solutions that are proportional to
cos
,
are similar to those for
dipoles in two dimensions, the m = 1 solutions that are proportional to
cos  from the second column of Table 5.7.1. However, note that the
two-dimensional dipole potential varies as r-1, while the three
dimensional dipole potential has an r-2 dependence. Also note that
whereas the polar coordinate dipole can have an arbitrary orientation
(can be a sine as well as a cosine function of
from the second column of Table 5.7.1. However, note that the
two-dimensional dipole potential varies as r-1, while the three
dimensional dipole potential has an r-2 dependence. Also note that
whereas the polar coordinate dipole can have an arbitrary orientation
(can be a sine as well as a cosine function of  , or any linear
combination of these), the three-dimensional dipole is z directed.
That is, do not replace the cosine function in (3) by a sine
function and expect that the potential will satisfy Laplace's
equation in spherical coordinates.
, or any linear
combination of these), the three-dimensional dipole is z directed.
That is, do not replace the cosine function in (3) by a sine
function and expect that the potential will satisfy Laplace's
equation in spherical coordinates.
Example 5.9.1. Equipotential Sphere in a Uniform Electrical Field
Consider a raindrop in an electric field. If
in the absence of the drop, that field is uniform over many drop radii
R, the field in the vicinity of the drop can be computed by taking the
field as being uniform "far from the sphere." The field is
z directed and has a magnitude Ea. Thus, on the scale of the
drop, the potential must approach that of
the uniform field (4) as r 
 .
.
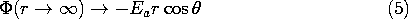 We will see in Chap. 7 that it takes only microseconds for a water
drop in air to become an equipotential. The condition that the
potential be zero at r = R and yet approach the potential of (5) as
r
We will see in Chap. 7 that it takes only microseconds for a water
drop in air to become an equipotential. The condition that the
potential be zero at r = R and yet approach the potential of (5) as
r 
 is met by adding to (5) the potential of a dipole at the origin,
an adjustable coefficient times (3). By writing the r dependencies
normalized to the drop radius R, it is possible to see directly what
this coefficient must be. That is, the proposed solution is
is met by adding to (5) the potential of a dipole at the origin,
an adjustable coefficient times (3). By writing the r dependencies
normalized to the drop radius R, it is possible to see directly what
this coefficient must be. That is, the proposed solution is
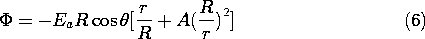 and it is clear that to make this function zero at r = R, A = -1.
and it is clear that to make this function zero at r = R, A = -1.
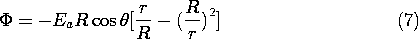 Note that even though the configuration of a perfectly conducting rod
in a uniform transverse electric field (as considered in Example
5.8.1) is very different from the perfectly conducting sphere in a
uniform electric field, the potentials are deduced from very similar
arguments, and indeed the potentials appear similar. In cross-section,
the distribution of potential and field intensity is similar to that
for the cylinder shown in Fig. 5.8.2. Of course, their appearance in
three-dimensional space is very different. For the polar coordinate
configuration, the equipotentials shown are the cross-sections of
cylinders, while for the spherical drop they are cross-sections of
surfaces of revolution. In both cases, the potential acquired (by the
sphere or the rod) is that of the symmetry plane normal
to the applied field.
Note that even though the configuration of a perfectly conducting rod
in a uniform transverse electric field (as considered in Example
5.8.1) is very different from the perfectly conducting sphere in a
uniform electric field, the potentials are deduced from very similar
arguments, and indeed the potentials appear similar. In cross-section,
the distribution of potential and field intensity is similar to that
for the cylinder shown in Fig. 5.8.2. Of course, their appearance in
three-dimensional space is very different. For the polar coordinate
configuration, the equipotentials shown are the cross-sections of
cylinders, while for the spherical drop they are cross-sections of
surfaces of revolution. In both cases, the potential acquired (by the
sphere or the rod) is that of the symmetry plane normal
to the applied field.
The surface charge on the spherical surface follows from (7).
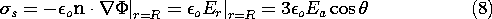 Thus, for Ea > 0, the north pole is capped by positive surface charge
while the south pole has negative charge. Although we think of the second
solution in (7) as being due to a fictitious dipole located at the
sphere's center, it actually represents the field of these surface
charges. By contrast with the rod, where the maximum field is twice
the uniform field, it follows from (8) that the field intensifies by
a factor of three at the poles of the sphere.
Thus, for Ea > 0, the north pole is capped by positive surface charge
while the south pole has negative charge. Although we think of the second
solution in (7) as being due to a fictitious dipole located at the
sphere's center, it actually represents the field of these surface
charges. By contrast with the rod, where the maximum field is twice
the uniform field, it follows from (8) that the field intensifies by
a factor of three at the poles of the sphere.
In making practical use of the solution found here, the "uniform
field at infinity Ea" is that of a field that is slowly varying over
dimensions on the order of the drop radius R. To demonstrate this idea
in specific terms, suppose that the imposed field is due to a distant
point charge. This is the situation considered in Example 4.6.4,
where the field produced by a point charge and a conducting sphere is
considered. If the point charge is very far away from the sphere, its
field at the position of the sphere is essentially uniform over the
region occupied by the sphere. (To relate the directions of the
fields in Example 4.6.4 to the present case, mount the  = 0
axis from
the center of the sphere pointing towards the point charge. Also, to
make the field in the vicinity of the sphere positive, make the point
charge negative, q
= 0
axis from
the center of the sphere pointing towards the point charge. Also, to
make the field in the vicinity of the sphere positive, make the point
charge negative, q  -q.)
At the sphere center, the magnitude of the field intensity due to
the point charge is
-q.)
At the sphere center, the magnitude of the field intensity due to
the point charge is
 The magnitude of the image charge, given by (4.6.34), is
The magnitude of the image charge, given by (4.6.34), is
 and it is positioned at the distance D = R2/X from the center of the
sphere. If the sphere is to be charge free, a charge of strength -Q1
has to be mounted at its center. If X is very large compared to R, the
distance D becomes small enough so that this charge and the charge given
by (10) form a dipole of strength
and it is positioned at the distance D = R2/X from the center of the
sphere. If the sphere is to be charge free, a charge of strength -Q1
has to be mounted at its center. If X is very large compared to R, the
distance D becomes small enough so that this charge and the charge given
by (10) form a dipole of strength
 The potential resulting from this dipole moment is given by (4.4.10),
with p evaluated using this moment. With the aid of (9), the dipole
field induced by the point charge is recognized as
The potential resulting from this dipole moment is given by (4.4.10),
with p evaluated using this moment. With the aid of (9), the dipole
field induced by the point charge is recognized as
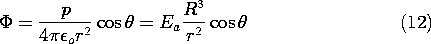 As witnessed by (7), this potential is identical to the one we have
found necessary to add to the potential of the uniform field in order
to match the boundary conditions on the sphere.
As witnessed by (7), this potential is identical to the one we have
found necessary to add to the potential of the uniform field in order
to match the boundary conditions on the sphere.
Of the three spherical coordinate solutions to Laplace's equation
given in this section, only two were required in the previous example.
The next makes use of all three.
Example 5.9.2. Charged Equipotential Sphere in a Uniform
Electric Field
Suppose that the highly conducting sphere from Example 5.9.1
carries a net charge q while immersed in
a uniform applied electric field Ea. Thunderstorm electrification
is evidence
that raindrops are often charged, and Ea could be the field they
generate collectively.
In the absence of this net charge, the potential is given by
(7). On the boundary at r = R, this potential remains uniform if we
add the potential of a point charge at the origin of magnitude q.
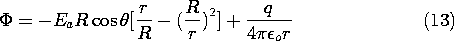 The surface potential has been raised from zero to q/4
The surface potential has been raised from zero to q/4
 o R, but
this
potential is independent of
o R, but
this
potential is independent of  and so the tangential electric field
remains zero.
and so the tangential electric field
remains zero.
The point charge is, of course, fictitious. The actual charge
is distributed over the surface and is found from (13) to be
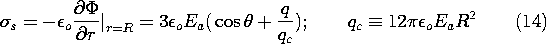 The surface charge density switches sign when the term in parentheses
vanishes, when q/qc < 1 and
The surface charge density switches sign when the term in parentheses
vanishes, when q/qc < 1 and
 Figure 5.9.2a is a graphical solution of this equation. For Ea and
q positive, the positive surface charge capping the sphere extends into
the southern hemisphere. The potential and electric field
distributions implied by (13) are illustrated in Fig. 5.9.2b. If q
exceeds qc \equiv 12
Figure 5.9.2a is a graphical solution of this equation. For Ea and
q positive, the positive surface charge capping the sphere extends into
the southern hemisphere. The potential and electric field
distributions implied by (13) are illustrated in Fig. 5.9.2b. If q
exceeds qc \equiv 12 
 o Ea R2, the entire surface of the
sphere is covered with positive surface charge density and E is
directed outward over the entire surface.
o Ea R2, the entire surface of the
sphere is covered with positive surface charge density and E is
directed outward over the entire surface.

5.10 Three-Dimensional Solutions to Laplace's Equation
Natural boundaries enclosing volumes in which Poisson's equation
is to be satisfied are shown in Fig. 5.10.1 for the three standard
coordinate systems. In general, the distribution of potential is
desired within the volume with an arbitrary potential distribution on
the bounding surfaces.
 Considered first in this section is the extension of the
Cartesian coordinate two-dimensional product solutions and modal
expansions introduced in Secs. 5.4 and 5.5 to three dimensions. Given
an arbitrary potential distribution over one of the six surfaces of
the box shown in Fig. 5.10.1, and given that the other five surfaces
are at zero potential, what is the solution to Laplace's equation
within? If need be, a superposition of six such solutions can be used
to satisfy arbitrary conditions on all six boundaries.
Considered first in this section is the extension of the
Cartesian coordinate two-dimensional product solutions and modal
expansions introduced in Secs. 5.4 and 5.5 to three dimensions. Given
an arbitrary potential distribution over one of the six surfaces of
the box shown in Fig. 5.10.1, and given that the other five surfaces
are at zero potential, what is the solution to Laplace's equation
within? If need be, a superposition of six such solutions can be used
to satisfy arbitrary conditions on all six boundaries.
To use the same modal approach in configurations where the
boundaries are natural to other than Cartesian coordinate systems, for
example the cylindrical and spherical ones shown in Fig. 5.10.1,
essentially the same extension of the basic ideas already illustrated
is used. However, the product solutions involve less familiar
functions. For those who understand the two-dimensional solutions,
how they are used to meet arbitrary boundary conditions and how they
are extended to three-dimensional Cartesian coordinate configurations,
the literature cited in this section should provide ready access to
what is needed to exploit solutions in new coordinate systems. In
addition to the three standard coordinate systems, there are many others
in which Laplace's equation admits product solutions. The latter part
of this section is intended as an introduction to these coordinate
systems and associated product solutions.
Cartesian Coordinate Product Solutions
In three-dimensions, Laplace's equation is
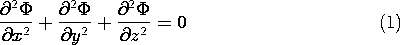 We look for solutions that are
expressible as products of a function of x alone, X(x), a function of
y alone, Y(y), and a function of z alone, Z(z).
We look for solutions that are
expressible as products of a function of x alone, X(x), a function of
y alone, Y(y), and a function of z alone, Z(z).
 Introducing (2) into (1) and dividing by
Introducing (2) into (1) and dividing by  , we obtain
, we obtain
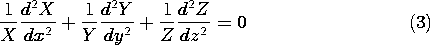 A function of x alone, added to one of y alone and one of of z
alone, gives zero. Because x, y, and z are independent
variables, the zero sum is possible only if each of these three
"functions" is in fact equal to a constant. The sum of these
constants must then be zero.
A function of x alone, added to one of y alone and one of of z
alone, gives zero. Because x, y, and z are independent
variables, the zero sum is possible only if each of these three
"functions" is in fact equal to a constant. The sum of these
constants must then be zero.
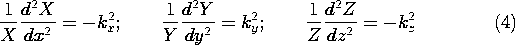
 Note that if two of these three
separation constants are positive, it is then necessary that the third
be negative. We anticipated this by writing (4) accordingly. The
solutions of (4) are
Note that if two of these three
separation constants are positive, it is then necessary that the third
be negative. We anticipated this by writing (4) accordingly. The
solutions of (4) are
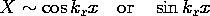
 where
where
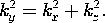 Of course, the roles of the coordinates can be interchanged, so
either the x or z directions could be
taken as having the exponential dependence. From these solutions it
is evident that the potential cannot be periodic or be exponential in
its dependencies on all three coordinates and still be a solution to
Laplace's equation. In writing (6) we have anticipated satisfying
potential constraints on planes of constant y by taking X and Z as
periodic.
Of course, the roles of the coordinates can be interchanged, so
either the x or z directions could be
taken as having the exponential dependence. From these solutions it
is evident that the potential cannot be periodic or be exponential in
its dependencies on all three coordinates and still be a solution to
Laplace's equation. In writing (6) we have anticipated satisfying
potential constraints on planes of constant y by taking X and Z as
periodic.
Modal Expansion in Cartesian Coordinates
It is possible to choose the constants and the solutions from (6)
so that zero potential boundary conditions are met on five of the six
boundaries. With coordinates as shown in Fig. 5.10.1a, the sine
functions are used for X and Z to insure a zero potential in the
planes x = 0 and z = 0. To make the potential zero in planes x =
a and z = w, it is necessary that
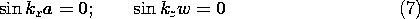 Solution of these eigenvalue equations gives kx = m
Solution of these eigenvalue equations gives kx = m /a, kz =
n
/a, kz =
n /w, and hence
/w, and hence
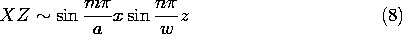 where m and n are integers.
where m and n are integers.
To make the potential zero on the fifth boundary, say where y = 0,
the hyperbolic sine function is used to represent the y dependence.
Thus, a set of solutions, each meeting a zero potential condition on
five boundaries, is
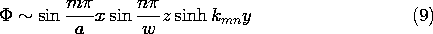 where in view of (5)
where in view of (5)
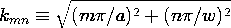 These can be used to satisfy an arbitrary potential constraint on the
"last" boundary, where y = b. The following example, which
extends Sec. 5.5, illustrates this concept.
These can be used to satisfy an arbitrary potential constraint on the
"last" boundary, where y = b. The following example, which
extends Sec. 5.5, illustrates this concept.
Example 5.10.1. Capacitive Attenuator in Three Dimensions
In the attenuator of Example 5.5.1, the two-dimensional field
distribution is a good approximation because one cross-sectional
dimension is small compared to the other. In Fig. 5.5.5, a \ll w. If
the cross-sectional dimensions a and w are comparable, as shown in
Fig. 5.10.2, the field can be represented by the modal superposition
given by (9).
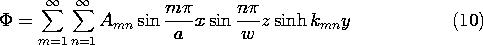
 In the five planes x = 0, x = a, y = 0, z = 0, and z = w
the potential is zero. In the plane y = b, it is constrained to be
v by an electrode connected to a voltage source.
In the five planes x = 0, x = a, y = 0, z = 0, and z = w
the potential is zero. In the plane y = b, it is constrained to be
v by an electrode connected to a voltage source.
Evaluation of (10) at the electrode surface must give v.
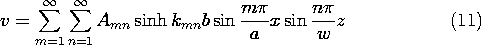 The coefficients Amn are determined by exploiting the orthogonality of
the eigenfunctions. That is,
The coefficients Amn are determined by exploiting the orthogonality of
the eigenfunctions. That is,
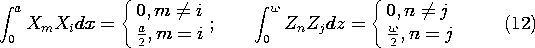 where
where
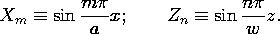 The steps that now lead
to an expression for any given coefficient Amn are a natural
extension of those used in Sec. 5.5. Both sides of (11) are
multiplied by the eigenfunction Xi Zj and then both sides are
integrated over the surface at y = b.
The steps that now lead
to an expression for any given coefficient Amn are a natural
extension of those used in Sec. 5.5. Both sides of (11) are
multiplied by the eigenfunction Xi Zj and then both sides are
integrated over the surface at y = b.
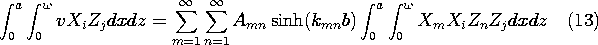 Because of the product form of
each term, the integrations can be carried out on x and z separately.
In view of the orthogonality conditions, (12), the only none-zero
term on the right comes in the summation with m = i and n = j. This makes
it possible to solve the equation for the coefficient Aij. Then,
by replacing i
Because of the product form of
each term, the integrations can be carried out on x and z separately.
In view of the orthogonality conditions, (12), the only none-zero
term on the right comes in the summation with m = i and n = j. This makes
it possible to solve the equation for the coefficient Aij. Then,
by replacing i 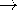 m and j \rightarrow n, we obtain
m and j \rightarrow n, we obtain
 The integral can be carried out
for any given distribution of potential. In this particular
situation, the potential of the surface at y = b is uniform. Thus,
integration gives
The integral can be carried out
for any given distribution of potential. In this particular
situation, the potential of the surface at y = b is uniform. Thus,
integration gives
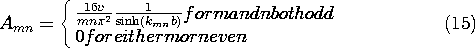 The desired potential,
satisfying the boundary conditions on all six surfaces, is given by
(10) and (15). Note that the first term in the solution we have
found is not the same as the first term in the two-dimensional field
representation, (5.5.9). No matter what the ratio of a to w, the
first term in the three-dimensional solution has a sinusoidal
dependence on z, while the two-dimensional one has no dependence on z.
The desired potential,
satisfying the boundary conditions on all six surfaces, is given by
(10) and (15). Note that the first term in the solution we have
found is not the same as the first term in the two-dimensional field
representation, (5.5.9). No matter what the ratio of a to w, the
first term in the three-dimensional solution has a sinusoidal
dependence on z, while the two-dimensional one has no dependence on z.
For the capacitive attenuator of Fig. 5.5.5, what output signal
is predicted by this three dimensional representation? From (10)
and (15), the charge on the output electrode is
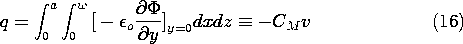 where
where
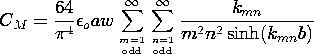 With v = V sin
With v = V sin 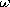 t, we find that vo = Vo cos
t, we find that vo = Vo cos 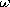 t
where
t
where
 Using (16), it follows that the amplitude of the output voltage is
Using (16), it follows that the amplitude of the output voltage is
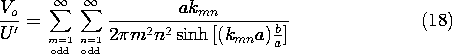 where the voltage is normalized to
where the voltage is normalized to
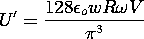 and
and
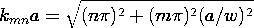 This expression can be
used to replace the plot of Fig. 5.5.5. Here we compare the
two-dimensional and three-dimensional predictions of
output voltage by considering (18) in the limit where b \gg a. In
this limit, the hyperbolic sine is dominated by one of its
exponentials, and the first term in the series gives
This expression can be
used to replace the plot of Fig. 5.5.5. Here we compare the
two-dimensional and three-dimensional predictions of
output voltage by considering (18) in the limit where b \gg a. In
this limit, the hyperbolic sine is dominated by one of its
exponentials, and the first term in the series gives
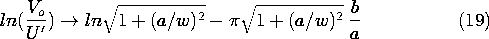 In the limit a/w \ll 1, the dependence on spacing between input and
output electrodes expressed by the right hand side becomes identical
to that for the two-dimensional model, (5.5.15). However,
U' = (8/
In the limit a/w \ll 1, the dependence on spacing between input and
output electrodes expressed by the right hand side becomes identical
to that for the two-dimensional model, (5.5.15). However,
U' = (8/ 2 )U regardless of a/w.
2 )U regardless of a/w.
This three-dimensional Cartesian coordinate example illustrates
how the orthogonality property of the product solution is
exploited to provide a potential that is zero on five of the
boundaries while assuming any desired distribution on the sixth
boundary. On this sixth surface, the potential takes the form
 where
where
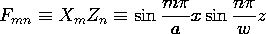 The two-dimensional functions Fmn have been used to represent the
"last" boundary condition. This two-dimensional Fourier series
replaces the one-dimensional Fourier series of Sec. 5.5 (5.5.17).
In the example, it represents the two-dimensional square wave function
shown in Fig. 5.10.3. Note that this function goes to zero along x = 0,
x = a and z = 0, z = w, as it should. It changes sign as it
passes through
any one of these "nodal" lines, but the range outside the original
rectangle is of no physical interest, and hence the behavior outside
that range does not affect the validity of the solution applied to the
example. Because the function represented is odd in both x and
y, it can be represented by sine functions only.
The two-dimensional functions Fmn have been used to represent the
"last" boundary condition. This two-dimensional Fourier series
replaces the one-dimensional Fourier series of Sec. 5.5 (5.5.17).
In the example, it represents the two-dimensional square wave function
shown in Fig. 5.10.3. Note that this function goes to zero along x = 0,
x = a and z = 0, z = w, as it should. It changes sign as it
passes through
any one of these "nodal" lines, but the range outside the original
rectangle is of no physical interest, and hence the behavior outside
that range does not affect the validity of the solution applied to the
example. Because the function represented is odd in both x and
y, it can be represented by sine functions only.
 Our foray into three-dimensional modal expansions extends the
notion of orthogonality of functions with respect to a one-dimensional
interval to orthogonality of functions with respect to a
two-dimensional section of a plane. We are able to determine the
coefficients Vmn in (20) as it is made to fit the potential
prescribed on the "sixth" surface because the terms in the series are
orthogonal in the sense that
Our foray into three-dimensional modal expansions extends the
notion of orthogonality of functions with respect to a one-dimensional
interval to orthogonality of functions with respect to a
two-dimensional section of a plane. We are able to determine the
coefficients Vmn in (20) as it is made to fit the potential
prescribed on the "sixth" surface because the terms in the series are
orthogonal in the sense that
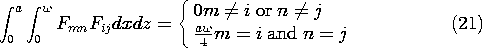 In other coordinate systems, a similar orthogonality relation will
hold for the product solutions evaluated on one of the
surfaces defined by a constant natural coordinate. In general, a
weighting function multiplies the eigenfunctions in the integrand of
the surface integral that is analogous to (21).
In other coordinate systems, a similar orthogonality relation will
hold for the product solutions evaluated on one of the
surfaces defined by a constant natural coordinate. In general, a
weighting function multiplies the eigenfunctions in the integrand of
the surface integral that is analogous to (21).
Except for some special cases, this is as far as we will go in
considering three-dimensional product solutions to
Laplace's equation. In the remainder of this section, references to
the literature are given for solutions in cylindrical, spherical, and
other coordinate systems.
Modal Expansion in Other Coordinates
A general volume having natural boundaries in cylindrical coordinates
is shown in Fig. 5.10.1b. Product solutions to Laplace's equation
take the form
 The polar coordinates of Sec. 5.7 are a special case where Z(z) is a
constant.
The ordinary differential equations, analogous to (4) and (5),
that determine F(
The polar coordinates of Sec. 5.7 are a special case where Z(z) is a
constant.
The ordinary differential equations, analogous to (4) and (5),
that determine F( ) and Z(z), have constant coefficients,
and hence the
solutions are sines and cosines of m
) and Z(z), have constant coefficients,
and hence the
solutions are sines and cosines of m and kz, respectively.
The radial
dependence is predicted by an ordinary differential equation that,
like (5.7.5), has space-varying coefficients. Unfortunately, with
the z dependence, solutions are not simply polynomials. Rather, they
are Bessel's functions of order m and argument kr. As applied to
product solutions to Laplace's equation, these functions
are described in standard fields texts[1-4]. Bessel's and
associated functions are developed in mathematics texts and
treatises[5-8].
and kz, respectively.
The radial
dependence is predicted by an ordinary differential equation that,
like (5.7.5), has space-varying coefficients. Unfortunately, with
the z dependence, solutions are not simply polynomials. Rather, they
are Bessel's functions of order m and argument kr. As applied to
product solutions to Laplace's equation, these functions
are described in standard fields texts[1-4]. Bessel's and
associated functions are developed in mathematics texts and
treatises[5-8].
As has been illustrated in two- and now three-dimensions, the
solution to an arbitrary potential distribution on the boundaries can
be written as the superposition of solutions each having the desired
potential on one boundary and zero potential on the others. Summarized
in Table 5.10.1 are the forms taken by the product solution, (22),
in representing the potential for an arbitrary distribution on the
specified surface. For example, if the potential is imposed on a
surface of constant r, the radial dependence is given by Bessel's
functions of real order and imaginary argument. What is needed to
represent  in the constant r surface are functions that are periodic
in
in the constant r surface are functions that are periodic
in  and z, so we expect that these Bessel's functions have an
exponential-like dependence on r.
and z, so we expect that these Bessel's functions have an
exponential-like dependence on r.
 In spherical coordinates, product solutions take the form
In spherical coordinates, product solutions take the form
 From the cylindrical coordinate solutions, it might be guessed that
new functions are required to describe R(r). In fact, these turn
out to be simple polynomials. The
From the cylindrical coordinate solutions, it might be guessed that
new functions are required to describe R(r). In fact, these turn
out to be simple polynomials. The  dependence is predicted by a
constant coefficient equation, and hence represented by familiar
trigonometric functions. But the
dependence is predicted by a
constant coefficient equation, and hence represented by familiar
trigonometric functions. But the  dependence is described by
Legendre functions. By contrast with the Bessel's functions, which
are described by infinite polynomial series, the Legendre functions
are finite polynomials in cos (
dependence is described by
Legendre functions. By contrast with the Bessel's functions, which
are described by infinite polynomial series, the Legendre functions
are finite polynomials in cos (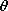 ). In connection with
Laplace's equation, the solutions are summarized in fields
texts[1-4]. As solutions to ordinary differential
equations, the Legendre polynomials are presented in mathematics
texts[5,7].
The names of other coordinate systems suggest the surfaces
generated by setting one of the variables equal to a constant:
Elliptic-cylinder coordinates and prolate spheroidal coordinates are
examples in which Laplace's equation is separable[2]. The first
step in exploiting these new systems
is to write the Laplacian and other differential operators in terms of
those coordinates. This is also described in the given references.
). In connection with
Laplace's equation, the solutions are summarized in fields
texts[1-4]. As solutions to ordinary differential
equations, the Legendre polynomials are presented in mathematics
texts[5,7].
The names of other coordinate systems suggest the surfaces
generated by setting one of the variables equal to a constant:
Elliptic-cylinder coordinates and prolate spheroidal coordinates are
examples in which Laplace's equation is separable[2]. The first
step in exploiting these new systems
is to write the Laplacian and other differential operators in terms of
those coordinates. This is also described in the given references.
5.11 Summary
There are two themes in this chapter. First is the division of
a solution to a partial differential equation into a particular part,
designed to balance the "drive" in the differential equation, and a
homogeneous part, used to make the total solution satisfy the boundary
conditions. This chapter solves Poisson's equation;
the "drive" is due to the volumetric charge density and the boundary
conditions are stated in terms of prescribed potentials. In the
following chapters, the approach used here will be applied to boundary
value problems representing many different physical situations.
Differential equations and boundary conditions will be different, but
because they will be linear, the same approach can be used.
Second is the theme of product solutions to Laplace's
equation which by virtue of their orthogonality can be superimposed to
satisfy arbitrary boundary conditions. The thrust of this statement
can be appreciated by the end of Sec. 5.5. In the configuration
considered in that section, the potential is zero on all but one of
the natural Cartesian boundaries of an enclosed region. It is shown
that the product solutions can be superimposed to satisfy
an arbitrary potential condition on the "last" boundary. By making
the "last" boundary any one of the boundaries and, if need be,
superimposing as many series solutions as there are boundaries, it is
then possible to meet arbitrary conditions on all of the boundaries.
The section on polar coordinates gives the opportunity to extend these
ideas to systems where the coordinates are not interchangeable, while
the section on three-dimensional Cartesian solutions indicates a
typical generalization to three dimensions.
In the chapters that follow, there will be a frequent need for
solving Laplace's equation. To this end, three classes of solutions
will often be exploited: the Cartesian solutions of Table 5.4.1, the
polar coordinate ones of Table 5.7.1, and the three spherical
coordinate solutions of Sec. 5.9. In Chap. 10, where magnetic
diffusion phenomena are introduced and in Chap. 13, where
electromagnetic waves are described, the application of these ideas
to the diffusion and the Helmholtz equations is illustrated.
R E F E R E N C E S
- M. Zahn, Electromagnetic Field Theory: A Problem Solving
Approach, John Wiley and Sons, N.Y. (1979).
- P. Moon and D. E. Spencer, Field Theory for Engineers, Van
Nostrand, Princeton, N.J. (1961).
- S. Ramo, J. R. Whinnery, and T. Van Duzer, Fields and Waves in
Communication Electronics, John Wiley and Sons, N.Y. (1967).
- J. R. Melcher, Continuum Electromechanics, M.I.T. Press,
Cambridge, Mass. (1981).
- F. B. Hildebrand, Advanced Calculus for Applications,
Prentice-Hall, Inc, Englewood Cliffs, N.J. (1962).
- G. N. Watson, A Treatise on the Theory of Bessel Functions,
Cambridge University Press, London E.C.4. (1944).
-
P. M. Morse and H. Feshbach, Methods of Theoretical
Physics, McGraw-Hill Book Co., N.Y. (1953).
- N. W. McLachlan, Bessel Functions for Engineers,
Oxford University Press, London E.C.4 (1941).
P R O B L E M S |
|---|
| | Poisson's and Laplace's Equations
|
|---|
| 5.1.1 | In Problem 4.7.1, the potential of a point charge over a perfectly
conducting plane (where z > 0) was found to be Eq. (a) of that
problem. Identify particular and homogeneous parts of this solution.
|
| 5.1.2 | A solution for the potential in the region -a < y < a, where there is
a charge density  , satisfies the boundary conditions , satisfies the boundary conditions  = 0 in
the planes y = +a and y = -a. = 0 in
the planes y = +a and y = -a.
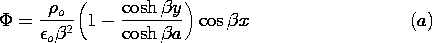
|
| 5.1.3* | The charge density between the planes x = 0 and x = d depends
only on x.
 Boundary conditions are that
Boundary conditions are that  (x = 0) = 0 and (x = 0) = 0 and  (x =
d) = V, so (x =
d) = V, so  = =  (x) is independent of y and z. (x) is independent of y and z.

| (a) | Show that Poisson's equation therefore reduces to
|
| (b) | Integrate this expression twice and use the boundary
conditions to show that the potential distribution is
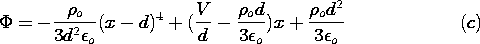
|
| (c) | Argue that the first term in (c) can be  p, with the
remaining terms then p, with the
remaining terms then  h. h.
|
| (d) | Show that in that case, the boundary conditions satisfied by
 h are h are
|
|
| 5.1.4 | With the charge density given as
 carry out the steps in Prob. 5.1.3.
carry out the steps in Prob. 5.1.3.

|
| 5.1.5* | A frequently used model for a capacitor is shown in Fig. P5.1.5,
where two plane parallel electrodes have a spacing that is small
compared to either of their planar dimensions. The potential
difference between the electrodes is v, and so over most of the
region between the electrodes, the electric field is uniform.
the region well removed from the edges of the electrodes, the field
E = -(v/d) iz satisfies Laplace's equation and the
boundary conditions on the electrode surfaces.
|
| 5.1.6* | In the three-electrode system of Fig.~P5.1.6, the bottom
electrode is taken as having the reference potential. The upper and
middle electrodes then have potentials v1 and v2, respectively.
The spacings between electrodes, 2d and d, are small enough relative
to the planar dimensions of the electrodes so that the fields between can
be approximated as being uniform.
the figure are then approximately E1 = v1/2d, E2 = v2/d
and Em = (v1 - v2)/d.
| (a) | Show that the fields denoted in
|
| (b) | Show that the net charges q1 and q2 on the top and
middle electrodes, respectively, are related to the voltages by the
capacitance matrix [in the form of (12)]
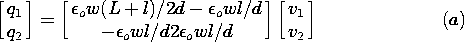
|
 \noprobsect
\noprobsect
|
| | Continuity Conditions |
|---|
| 5.2.1* | The electric potentials  a and a and  b above and below
the plane y = 0 are b above and below
the plane y = 0 are
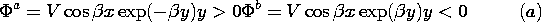 0.)
0.)
| (a) | Show that (4) holds. (The potential is continuous at y =
|
| (b) | Evaluate E tangential to the surface y = 0 and show
that it too is continuous. [Equation (1) is then automatically
satisfied at y = 0.]
|
| (c) | Use (5) to show that in the plane y = 0, the surface
charge density,  s = 2 s = 2 o o  V cos V cos  x, accounts for
the discontinuity in the derivative of x, accounts for
the discontinuity in the derivative of  normal to the plane y
= 0. normal to the plane y
= 0.
|
|
| 5.2.2 | By way of appreciating how the continuity of  guarantees the
continuity of tangential E [(4) implies that (1) is
satisfied], suppose that the potential is given in the plane y = 0: guarantees the
continuity of tangential E [(4) implies that (1) is
satisfied], suppose that the potential is given in the plane y = 0:
 = =  (x, 0, z).
from this information alone? (x, 0, z).
from this information alone?
| (a) | Which components of E can be determined
|
| (b) | For example, if  (x, 0, z) = V sin ( (x, 0, z) = V sin ( x) sin
( x) sin
( z), what are those components of E? z), what are those components of E?
|
|
| | Coordinates
|
|---|
| 5.3.1* | A region that extends to \pm 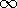 in the z direction has the
square cross-section of dimensions as shown in Fig. P5.4.1. The walls
at x = 0 and y = 0 are at zero potential, while those at x = a
and y = a have
the linear distributions shown. The interior region is free of charge
density. in the z direction has the
square cross-section of dimensions as shown in Fig. P5.4.1. The walls
at x = 0 and y = 0 are at zero potential, while those at x = a
and y = a have
the linear distributions shown. The interior region is free of charge
density.

| (a) | Show that the potential inside is
|
| (b) | Show that plots of  and E are as shown in the
first quadrant of Fig. 4.1.3. and E are as shown in the
first quadrant of Fig. 4.1.3.
|


|
| 5.3.2 | One way to constrain a boundary so that it has a potential
distribution that is a linear function of position is shown in Fig.
P5.4.2a. A uniformly resistive sheet having a length 2a is driven by
a voltage source V. For the coordinate x shown, the resulting
potential distribution is the linear function of x shown. The constant
C is determined by the definition of where the potential is zero. In
the case shown in Fig. 5.4.2a, if  is zero at x = 0, then C =
0. is zero at x = 0, then C =
0.
cross-section of
length 2a on a side, as shown in Fig. 5.4.2b, is constrained in
potential by resistive sheets and voltage sources, as shown. Note
that the potential is defined to be zero at the lower right-hand corner,
where (x, y) = (a, -a). Inside the cylinder, what must the potential be
in the planes x = \pm a and y = \pm a?
|
| 5.3.3* | Shown in cross-section in Fig. P5.4.3 is a cylindrical system
that extends to infinity in the \pm z directions. There is no charge
density inside the cylinder, and the potentials on the boundaries are
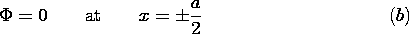
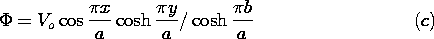
|
| 5.3.4 | The square cross-section of a cylindrical region that extends to
infinity in the \pm z directions is shown in Fig. P5.4.4. The
potentials on the boundaries are as shown.
Find  . .
| (a) | Inside the cylindrical space, there is no charge density.
|
| (b) | What is E in this region?
|
| (c) | Sketch  and E. and E.
|


|
| 5.3.5* | The cross-section of an electrode structure which is symmetric
about the x = 0 plane is shown in Fig. P5.4.5. Above this plane are
electrodes that alternately either have the potential v(t) or the
potential -v(t). The system has depth d (into the paper) which is
very long compared to such dimensions as a or l. So that the
current i(t) can be measured, one of the upper electrodes has a
segment which is insulated from the rest of the electrode, but driven
by the same potential. The geometry of the upper electrodes is
specified by giving their altitudes above the x = 0 plane. For example,
the upper electrode between y = -b and y = b has the shape
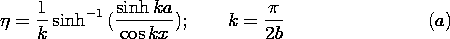 where
where  is as shown in Fig. P5.4.5. is as shown in Fig. P5.4.5.
electrodes is
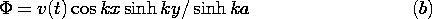
| (a) | Show that the potential in the region between the
|
| (b) | Show that E in this region is
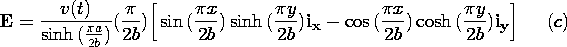
|
| (c) | Show that plots of  and E are as shown in
Fig. 5.4.2. and E are as shown in
Fig. 5.4.2.
|
| (d) | Show that the net charge on the upper electrode segment
between y = -l and y = l is
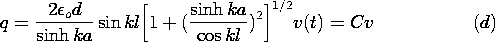 (Because the surface S in Gauss' integral law is arbitrary, it can be
chosen so that it both encloses this electrode and is convenient for
integration.)
(Because the surface S in Gauss' integral law is arbitrary, it can be
chosen so that it both encloses this electrode and is convenient for
integration.)
|
| (e) | Given that v(t) = Vo sin  t, where Vo and t, where Vo and
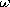 are constants, show that the current to the electrode segment
i(t), as defined in Fig. P5.4.5, is are constants, show that the current to the electrode segment
i(t), as defined in Fig. P5.4.5, is
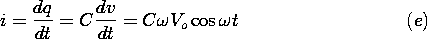
|
|
| 5.3.6 | In Prob. 5.4.5, the polarities of all of the voltage sources
driving the lower electrodes are reversed.
between the electrodes.
| (a) | Find  in the region in the region
|
| (b) | Determine E.
|
| (c) | Sketch  and E. and E.
|
| (d) | Find the charge q on the electrode segment in the upper
middle electrode.
|
| (e) | Given that v(t) = Vo cos  t, what is i(t)? t, what is i(t)?
|
|
| | Modal Expansion to Satisfy Boundary Conditions |
|---|
| 5.4.1* | The system shown in Fig. P5.5.1a is composed of a pair of
perfectly conducting parallel plates in the planes x = 0 and x =
a that are shorted in the plane y = b. Along the left edge, the
potential is imposed and so has a given distribution  d (x).
The plates and short have zero potential. d (x).
The plates and short have zero potential.
 d (x), the potential distribution for 0 < y < b, 0 < x < a is d (x), the potential distribution for 0 < y < b, 0 < x < a is
 where
where
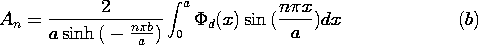 (At this stage, the coefficients in a modal expansion
for the field are left expressed as integrals over the yet to be
specified potential distribution.)
(At this stage, the coefficients in a modal expansion
for the field are left expressed as integrals over the yet to be
specified potential distribution.)
| (a) | Show that, in terms of
|
| (b) | In particular, if the imposed
potential is as shown in Fig. P5.5.1b, show that An is

|

|
| 5.4.2* | The walls of a rectangular cylinder are constrained in potential
as shown in Fig. P5.5.2. The walls at x = a and y = b have
zero potential, while those at y = 0 and x = 0 have the potential
distributions V1 (x) and V2 (y), respectively.
In particular, suppose that these distributions of potential are
uniform, so that V1(x) = Va and V2(y) = Vb, with Va and
Vb defined to be independent of x and y.
potential distribution there is
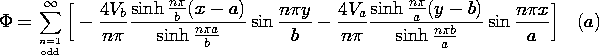
| (a) | The region inside the cylinder is free space. Show that the
|
| (b) | Show that the distribution of surface charge density along the
wall at x = a is
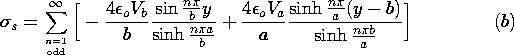
|

|
| 5.4.3 | In the configuration described in Prob. 5.5.2, the distributions
of potentials on the walls at x = 0 and y = 0 are as shown in
Fig. P5.5.3, where the peak voltages Va and Vb
are given functions of time.
cylinder.
| (a) | Determine the potential in the free space region inside the
|
| (b) | Find the surface charge distribution on the wall at y =
b.
|
 \problem 4*
The cross-section of a system that extends to "infinity" out of
the paper is shown in Fig. P5.5.4. An electrode in the plane y = d has
the potential V. A second electrode has the shape of an "L." One of
its sides is in the plane y = 0, while the other is in the plane x = 0,
extending from y = 0 almost to y = d. This electrode is at zero
potential.
\problem 4*
The cross-section of a system that extends to "infinity" out of
the paper is shown in Fig. P5.5.4. An electrode in the plane y = d has
the potential V. A second electrode has the shape of an "L." One of
its sides is in the plane y = 0, while the other is in the plane x = 0,
extending from y = 0 almost to y = d. This electrode is at zero
potential.
Show that, far to the left, the potential between the electrodes
tends to


|
| 5.4.5 | In the two-dimensional system shown in cross-section in Fig.
P5.5.5, plane parallel plates extend to infinity in the
-y direction.
The potentials of the upper and lower plates are, respectively, -Vo/2
and Vo/2. The potential over the plane y = 0 terminating
the plates at the right is specified to be  d(x). d(x).
to the left?
| (a) | What is the potential distribution between the plates far
|
| (b) | If  is taken as the potential is taken as the potential  a that
assumes the correct distribution as y a that
assumes the correct distribution as y  - -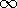 , plus a
potential , plus a
potential  b, what boundary conditions must be satisfied by b, what boundary conditions must be satisfied by
 b? b?
|
| (c) | What is the potential distribution between the plates?
|

|
| 5.4.6 | As an alternative (and in this case much more complicated) way of
expressing the potential in Prob. 5.4.1, use a modal approach to
express the potential in the interior region of Fig. P5.4.1.
|
| 5.4.7* | Take an approach to finding the potential in the configuration of
Fig. 5.5.2 that is an alternative to that used in the text. Let
 = (Vy/b) + = (Vy/b) +  1.
must be satisfied by 1.
must be satisfied by  1 are that 1 are that  1 = -Vy/b at x = 0
and at x = a, and 1 = -Vy/b at x = 0
and at x = a, and  1 = 0 at y = 0 and y = b. 1 = 0 at y = 0 and y = b.
| (a) | Show that the boundary conditions that
|
| (b) | Show that the potential is
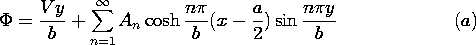 where
where
 (It is convenient to exploit the symmetry of the configuration about
the plane x = a/2.)
(It is convenient to exploit the symmetry of the configuration about
the plane x = a/2.)
|
|
| | Conditions
|
|---|
| 5.5.1* | The potential distribution is to be determined in a region
bounded by the planes y = 0 and y = d and extending to infinity
in the x
and z directions, as shown in Fig. P5.6.1. In this region, there is a
uniform charge density  o. On the upper boundary, the
potential is o. On the upper boundary, the
potential is  (x, d, z) = Va sin ( (x, d, z) = Va sin ( x). On the lower boundary, x). On the lower boundary,
 (x, 0, z) = Vb sin ( (x, 0, z) = Vb sin ( x). Show that x). Show that  (x, y, z)
throughout the region 0 < y < d is (x, y, z)
throughout the region 0 < y < d is
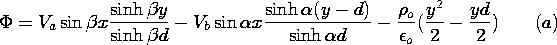

|
| 5.5.2 | For the configuration of Fig. P5.6.1, the charge is again uniform
in the region between the boundaries, with density  o, but the
potential at y = d is o, but the
potential at y = d is  = =  o sin (kx), while that at y =
0 is zero ( o sin (kx), while that at y =
0 is zero ( o and k are given constants). Find o and k are given constants). Find  in the
region where 0 < y < d, between the boundaries. in the
region where 0 < y < d, between the boundaries.
|
| 5.5.3* | In the region between the boundaries at y = \pm d/2 in Fig.
P5.6.3, the charge density is
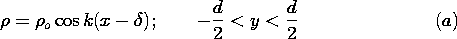 where
where  o and o and 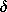 are given constants. Electrodes at
y = \pm d/2 constrain the tangential electric field there to be are given constants. Electrodes at
y = \pm d/2 constrain the tangential electric field there to be
 The charge density might represent a traveling wave of space
charge on a modulated particle beam, and the walls represent the
traveling-wave structure which interacts with the beam. Thus, in a
practical device, such as a traveling-wave amplifier designed to
convert the kinetic energy of the moving charge to ac electrical
energy available at the electrodes, the charge and potential
distributions move to the right with the same velocity. This does not
concern us, because we consider the interaction at one instant in
time.
The charge density might represent a traveling wave of space
charge on a modulated particle beam, and the walls represent the
traveling-wave structure which interacts with the beam. Thus, in a
practical device, such as a traveling-wave amplifier designed to
convert the kinetic energy of the moving charge to ac electrical
energy available at the electrodes, the charge and potential
distributions move to the right with the same velocity. This does not
concern us, because we consider the interaction at one instant in
time.


|
| 5.5.4 | In the region 0 < y < d shown in cross-section in Fig. P5.6.4, the
charge density is
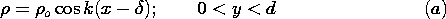 where
where  o and o and  are constants. Electrodes at y = d
constrain the potential there to be are constants. Electrodes at y = d
constrain the potential there to be  (x, d) = Vo cos (kx)
(Vo and k given constants), while an electrode at y = 0 makes (x, d) = Vo cos (kx)
(Vo and k given constants), while an electrode at y = 0 makes
 (x, 0) = 0. (x, 0) = 0.
everywhere between the electrodes.

|
| 5.5.5* | A region that extends to infinity in the \pm z directions has a
rectangular cross-section of dimensions 2a and b, as shown in Fig.
P5.6.5. The boundaries are at zero potential while the region inside
has the distribution of charge density
 where
where  o is a given constant. Show that the potential in this
region is o is a given constant. Show that the potential in this
region is

|
| 5.5.6 | The cross-section of a two-dimensional configuration is shown in
Fig. P5.6.6. The potential distribution is to be determined inside
the boundaries, which are all at zero potential.
 where V and
where V and  are given constants, what is the charge density
in that region? are given constants, what is the charge density
in that region?
| (a) | Given that a particular solution inside the boundaries is
|
| (b) | What is  ? ?
|

|
| 5.5.7 | The cross-section of a metal box that is very long in the z
direction is shown in Fig. P5.6.7. It is filled by the charge density
 o x/l. Determine o x/l. Determine  inside the box, given that inside the box, given that  = 0
on the walls. = 0
on the walls.

|
| 5.5.8* | In region (b), where y < 0, the charge density is  = =  o
cos ( o
cos ( x) e x) e y, where y, where  o, o,  , and , and  are
positive constants. In region (a), where 0 < y, are
positive constants. In region (a), where 0 < y,  = 0. = 0.
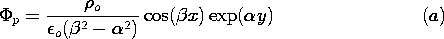
| (a) | Show that a particular solution in the region y < 0 is
|
| (b) | There is no surface charge density in the plane y = 0.
Show that the potential is
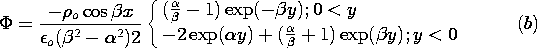
|
|
| 5.5.9 | A sheet of charge having the surface charge density  s = s =
 o sin o sin  (x - xo) is in the plane y = 0, as shown
in Fig. 5.6.3. At a distance a above and below the sheet, electrode
structures are used to constrain the potential to be (x - xo) is in the plane y = 0, as shown
in Fig. 5.6.3. At a distance a above and below the sheet, electrode
structures are used to constrain the potential to be  = V cos = V cos
 x. The system extends to infinity in the x and z
directions. The regions above and below the sheet are designated (a)
and (b), respectively. x. The system extends to infinity in the x and z
directions. The regions above and below the sheet are designated (a)
and (b), respectively.
 , ,  o, and xo. o, and xo.
| (a) | Find  a and a and  b in terms of the constants V, b in terms of the constants V,
|
| (b) | Given that the force per unit area acting on the charge
sheet is  s Ex (x, 0), what is the force acting on a section
of the sheet having length d in the z direction and one
wavelength 2 s Ex (x, 0), what is the force acting on a section
of the sheet having length d in the z direction and one
wavelength 2 / / in the x direction? in the x direction?
|
| (c) | Now, the potential on
the wall is made a traveling wave having a given angular frequency
 , ,  (x, \pm a, t) = V cos ( (x, \pm a, t) = V cos ( x - x -  t),
and the charge moves to the right with a velocity U, so that t),
and the charge moves to the right with a velocity U, so that
 s = s =  o sin o sin  (x - Ut - xo), where U = (x - Ut - xo), where U = 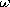 /
/ . Thus, the
wall potentials and surface charge density move in synchronism.
Building on the results from parts (a)-(b), what is the potential
distribution and hence total force on the section of charged sheet? . Thus, the
wall potentials and surface charge density move in synchronism.
Building on the results from parts (a)-(b), what is the potential
distribution and hence total force on the section of charged sheet?
|
| (d) | What you have developed is a primitive model for an
electron beam
device used to convert the kinetic energy of the electrons
(accelerated to the velocity v by a dc voltage) to high-frequency
electrical power
output. Because the system is free of dissipation, the electrical power
output (through the electrode structure) is equal to the mechanical
power input. Based on the force found in part (c), what is the
electrical power output produced by one period 2 / / of the
charge sheet of width w? of the
charge sheet of width w?
|
| (e) | For what values of xo would the
device act as a generator of electrical power?
|
|
| | Solutions to Laplace's Equation in Polar Coordinates |
|---|
| 5.6.1* | A circular cylindrical surface r = a has the potential  = V
sin 5 = V
sin 5 . The regions r < a and a < r are free of charge
density. Show that the potential is . The regions r < a and a < r are free of charge
density. Show that the potential is
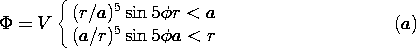
|
| 5.6.2 | The x - z plane is one of zero potential. Thus, the y axis is
perpendicular to a zero potential plane. With  measured
relative to the x axis and z the third coordinate axis, the
potential on the surface at r = R is constrained by segmented
electrodes there to be measured
relative to the x axis and z the third coordinate axis, the
potential on the surface at r = R is constrained by segmented
electrodes there to be  = V sin = V sin  .
region? .
region?
| (a) | If  = 0 in the region r < R, what is = 0 in the region r < R, what is  in that in that
|
| (b) | Over the range r < R, what is the
surface charge density on the surface at y = 0?
|
|
| 5.6.3* | An annular region b < r < a where  = 0 is bounded from outside
at r = a by a surface having the potential = 0 is bounded from outside
at r = a by a surface having the potential  = Va cos 3 = Va cos 3 and from the inside at r = b by a surface having the potential
and from the inside at r = b by a surface having the potential  = Vb sin
= Vb sin  . Show that . Show that  in the annulus can be written
as the sum of two terms, each a combination of solutions to Laplace's
equation designed to have the correct value at one radius while being
zero at the other. in the annulus can be written
as the sum of two terms, each a combination of solutions to Laplace's
equation designed to have the correct value at one radius while being
zero at the other.
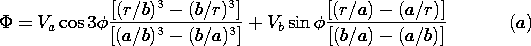
|
| 5.6.4 | In the region b < r < a, 0 <  < <  , ,  = 0. On the
boundaries of this region at r = a, at = 0. On the
boundaries of this region at r = a, at  = 0 and = 0 and  = =  ,
,  = 0. At r = b, = 0. At r = b,  = Vb sin ( = Vb sin (  / / ).
Determine ).
Determine  in this region. in this region.
|
| 5.6.5* | In the region b < r < a, 0 <  < <  , ,  = 0. On the
boundaries of this region at r = a, r = b and at = 0. On the
boundaries of this region at r = a, r = b and at  = 0, = 0,
 = 0. At = 0. At  = =  , the potential is , the potential is  = V sin
[3 = V sin
[3 ln(r/a)/ln(b/a)]. Show that within the region, ln(r/a)/ln(b/a)]. Show that within the region,
|
| 5.6.6 | The plane  = 0 is at potential = 0 is at potential  = V, while that at = V, while that at  =
3 =
3 /2 is at zero potential. The system extends to infinity in the
\pm z and r directions. Determine and sketch /2 is at zero potential. The system extends to infinity in the
\pm z and r directions. Determine and sketch  and E
in the range 0 < and E
in the range 0 <  < 3 < 3 /2. /2.
|
| | Examples in Polar Coordinates |
|---|
| 5.7.1* | Show that  and E as given by (4) and (5), respectively,
describe the potential and electric field intensity around a perfectly
conducting half-cylinder at r = R on a perfectly conducting plane at
x = 0 with a uniform field Ea ix applied at x and E as given by (4) and (5), respectively,
describe the potential and electric field intensity around a perfectly
conducting half-cylinder at r = R on a perfectly conducting plane at
x = 0 with a uniform field Ea ix applied at x 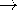
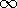 . Show that the maximum field intensity is twice that of the
applied field, regardless of the radius of the half-cylinder. . Show that the maximum field intensity is twice that of the
applied field, regardless of the radius of the half-cylinder.
|
| 5.7.2 | Coaxial circular cylindrical surfaces bound an annular region of
free space where b < r < a. On the inner surface, where r = b,
 = Vb > 0. On the outer surface, where r = a, = Vb > 0. On the outer surface, where r = a,  = Va >
0. = Va >
0.
| (a) | What is  in the annular region? in the annular region?
|
| (b) | How large must Vb be to
insure that all lines of E are outward directed from the inner
cylinder?
|
| (c) | What is the net charge per unit length on the inner
cylinder under the conditions of (b)?
|
|
| 5.7.3* | A device proposed for using the voltage vo to measure the
angular velocity \Omega of a shaft is shown in Fig. P5.8.3a. A
cylindrical grounded electrode has radius R. (The
resistance Ro is "small.") Outside and concentric at r = a is a
rotating shell supporting the surface charge density distribution
shown in Fig. P5.8.3b.
(b), respectively, outside and inside the rotating shell,

|
| 5.7.4 | Complete the steps of Prob. 5.8.3 with the configuration of Fig.
P5.8.3 altered so that the rotating shell is inside rather than
outside the grounded electrode. Thus, the radius a of the rotating
shell is less than the radius R, and region (a) is a < r < R,
while region (b) is r < a.
|
| 5.7.5* | A pair of perfectly conducting zero potential electrodes form a
wedge, one in the plane  = 0 and the other in the plane = 0 and the other in the plane
 = =  . They essentially extend to infinity in the \pm z
directions. Closing the region between the electrodes at r = R is an
electrode having potential V. Show that the potential inside the
region bounded by these three surfaces is . They essentially extend to infinity in the \pm z
directions. Closing the region between the electrodes at r = R is an
electrode having potential V. Show that the potential inside the
region bounded by these three surfaces is
|
| 5.7.6 | In a two-dimensional system, the region of interest is bounded in
the  = 0 plane by a grounded electrode and in the = 0 plane by a grounded electrode and in the  = =
 plane by one that has plane by one that has  = V. The region extends to
infinity in the r direction. At r = R, = V. The region extends to
infinity in the r direction. At r = R,  = V. Determine = V. Determine
 . .
|
| 5.7.7 | Figure P5.8.7 shows a circular cylindrical wall having potential
Vo relative to a grounded fin in the plane  = 0 that reaches from
the wall to the center. The gaps between the cylinder and the fin are
very small.
the boun\-dary conditions at = 0 that reaches from
the wall to the center. The gaps between the cylinder and the fin are
very small.
the boun\-dary conditions at  = 0 and = 0 and  = 2 = 2 . Note
that you cannot accept solutions for . Note
that you cannot accept solutions for  of negative powers in
r. of negative powers in
r.
| (a) | Find all solutions in polar coordinates that satisfy
|
| (b) | Match the boundary condition at r = R.
|
| (c) | One of the terms in this solution
has an electric field intensity that is infinite at the tip of the
fin, where r = 0. Sketch  and E in the neighborhood of the
tip. What is the and E in the neighborhood of the
tip. What is the  s on the fin associated with this term as
a function of r? What is the net charge associated with this term? s on the fin associated with this term as
a function of r? What is the net charge associated with this term?
|
| (d) | Sketch the potential and field intensity throughout the
region.
|

|
| 5.7.8 | A two-dimensional system has the same cross-sectional geometry as
that shown in Fig. 5.8.6 except that the wall at  = 0 has the
potential v. The wall at = 0 has the
potential v. The wall at  = =  o is grounded. Determine the
interior potential. o is grounded. Determine the
interior potential.
|
| 5.7.9 | Use arguments analogous to those used in going from (5.5.22) to
(5.5.26) to show the orthogonality (14) of the radial modes
Rn defined by (13). [Note the comment following (14).]
|
| | Spherical Coordinates
|
|---|
| 5.8.1 | On the surface of a spherical shell having radius r = a, the
potential is  = V cos = V cos 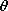 .
or inside this shell, what is .
or inside this shell, what is  for r < a and for r > a? for r < a and for r > a?
| (a) | With no charge density either outside
|
| (b) | Sketch  and E. and E.
|
|
| 5.8.2* | A spherical shell having radius a supports the surface charge
density  o cos o cos 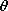 . .
volume of interest, the potential is
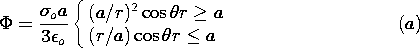
| (a) | Show that if this is the only charge in the
|
| (b) | Show that a plot of  and E appears as shown in
Fig. 6.3.1. and E appears as shown in
Fig. 6.3.1.
|
|
| 5.8.3* | A spherical shell having zero potential has radius a. Inside,
the charge density is  = =  o cos o cos 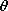 . Show that the
potential there is . Show that the
potential there is
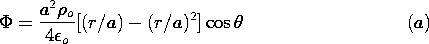
|
| 5.8.4 | The volume of a spherical region is filled with the charge
density  = =  o (r/a)m cos o (r/a)m cos 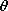 , where , where  o and m
are given constants. If the potential o and m
are given constants. If the potential  = 0 at r = a, what is = 0 at r = a, what is
 for r < a? for r < a?
|
| | Equation
|
|---|
| 5.9.1* | In the configuration of Fig. 5.10.2, all surfaces have zero
potential except those at x = 0 and x = a, which have  = v.
Show that = v.
Show that
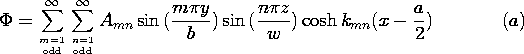 and
and
|
| 5.9.2 | In the configuration of Fig. 5.10.2, all surfaces have zero
potential. In the plane y = a/2, there is the surface charge density
 s = s =  o sin ( o sin ( x/a) sin ( x/a) sin ( z/w). Find the
potentials z/w). Find the
potentials  a and a and  b above and below this surface,
respectively. b above and below this surface,
respectively.
|
| 5.9.3 | The configuration is the same as shown in Fig. 5.10.2 except that
all of the walls are at zero potential and the volume is filled by the
uniform charge density  = =  o. Write four essentially
different expressions for the potential distribution. o. Write four essentially
different expressions for the potential distribution.
|
\globallineheight15pt\globallinedepth12pt
\boxtable
\verticallines
\globallineheight15pt\globallinedepth12pt
\boxtable
\verticallines
\globallineheight14pt\globallinedepth11pt
\boxtable
\verticallines
%%%%%%%%%%%%%%%%%%%%%deleted for editor's version%%%%%%%%%%%%%%%
| 5.9.6* | Show that in Cartesian coordinates (defined relative to the polar
coordinates in Fig. 5.7.1) the potential for the fringing field of the
closely spaced capacitor plates in Fig. 5.7.2b is
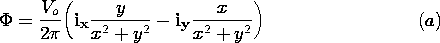 Now, consider the field surrounding a pair of capacitor plates having
infinite length in the z direction, width l in the x direction and
a spacing that is small compared to dimensions of interest. The
cross-section is shown in Fig. P5.7.6. Write the potential in terms
of the angles
Now, consider the field surrounding a pair of capacitor plates having
infinite length in the z direction, width l in the x direction and
a spacing that is small compared to dimensions of interest. The
cross-section is shown in Fig. P5.7.6. Write the potential in terms
of the angles  1 and 1 and  2 defined in the figure and then
convert the representation to Cartesian coordinates to show that 2 defined in the figure and then
convert the representation to Cartesian coordinates to show that


|

 is related to the charge density
is related to the charge density  by
Poisson's equation
by
Poisson's equation

 obeys Laplace's equation, (2),
with
obeys Laplace's equation, (2),
with  = 0.
= 0.
 = 0, and
can be regarded either as caused by fictitious charges residing
outside the region of interest or as caused by the surface
charges induced on the boundaries.
= 0, and
can be regarded either as caused by fictitious charges residing
outside the region of interest or as caused by the surface
charges induced on the boundaries.

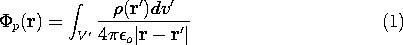





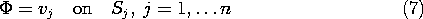

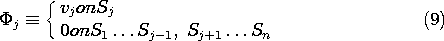

 da over the surface Si enclosing this electrode then gives
da over the surface Si enclosing this electrode then gives
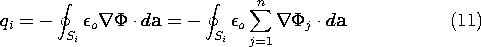

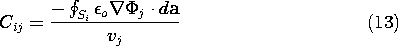
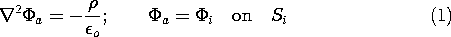
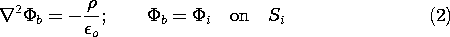
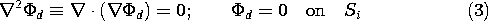





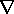
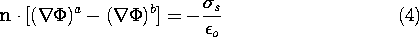


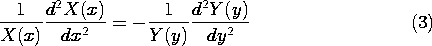


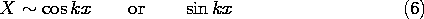
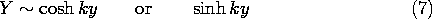
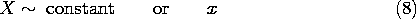
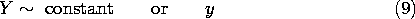

 /2, +
3
/2, +
3
 \pm
\pm  .
Thus, for the plots shown in Figs. 5.4.1 and 5.4.2, the charge
distributions at infinity must consist of alternating distributions of
positive and negative charges of infinite amplitude.
.
Thus, for the plots shown in Figs. 5.4.1 and 5.4.2, the charge
distributions at infinity must consist of alternating distributions of
positive and negative charges of infinite amplitude.



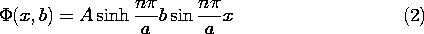

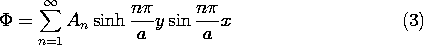
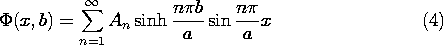
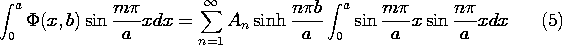
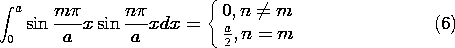
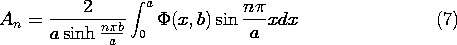
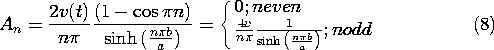
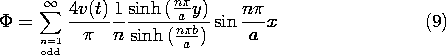


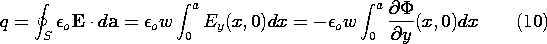
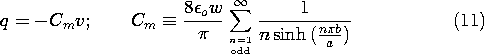
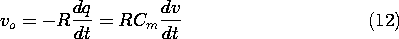
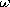 t, then
t, then
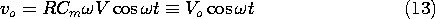
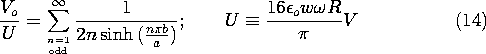

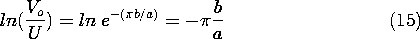
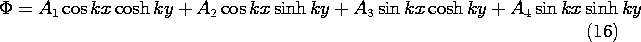
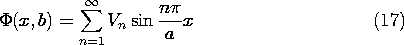

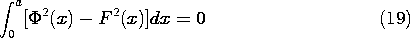

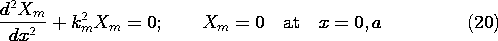
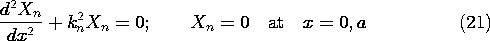
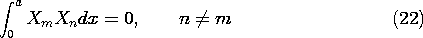
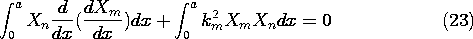
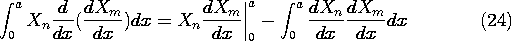
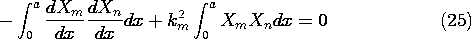
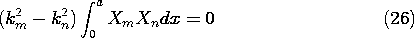
 o
throughout the region of interest, and a homogeneous part that
makes the sum of the two potentials satisfy the boundary conditions.
In short,
o
throughout the region of interest, and a homogeneous part that
makes the sum of the two potentials satisfy the boundary conditions.
In short,






 are given constants. For now,
the segment
connected to ground through the resistor in the lower electrode can be
regarded as being at the same zero potential as the remainder of the
electrode in the plane x = -a and the electrode in the plane y = a.
First we ask for the field distribution.
are given constants. For now,
the segment
connected to ground through the resistor in the lower electrode can be
regarded as being at the same zero potential as the remainder of the
electrode in the plane x = -a and the electrode in the plane y = a.
First we ask for the field distribution.

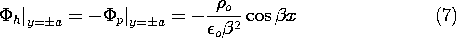

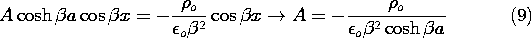
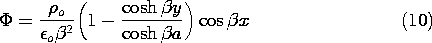


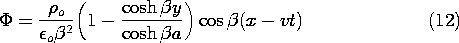
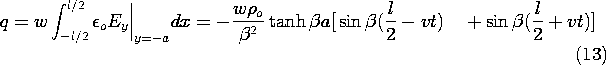
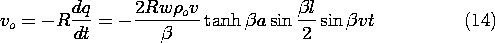
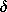 . The beam moves with
the velocity v in the x direction between two planar perfect
conductors situated at y = \pm a
and held at zero potential. The configuration is shown in
cross-section in Fig. 5.6.3. In addition to the uniform charge
density, there is a "ripple" of charge density, so that the net charge
density is
. The beam moves with
the velocity v in the x direction between two planar perfect
conductors situated at y = \pm a
and held at zero potential. The configuration is shown in
cross-section in Fig. 5.6.3. In addition to the uniform charge
density, there is a "ripple" of charge density, so that the net charge
density is

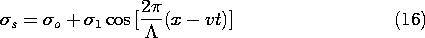
 o =
o = 
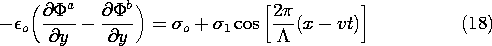







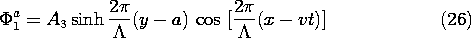
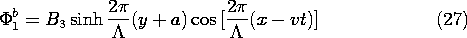
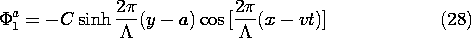
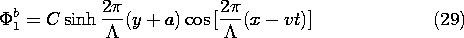
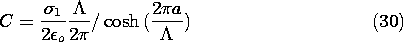
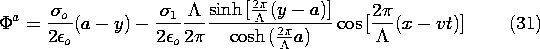
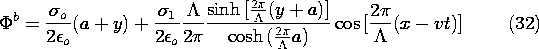

 , it is convenient to match these conditions with solutions
to Laplace's equation in polar coordinates (cylindrical coordinates
with no z dependence). The approach adopted is entirely analogous to
the one used in Sec. 5.4 in the case of Cartesian coordinates.
, it is convenient to match these conditions with solutions
to Laplace's equation in polar coordinates (cylindrical coordinates
with no z dependence). The approach adopted is entirely analogous to
the one used in Sec. 5.4 in the case of Cartesian coordinates.

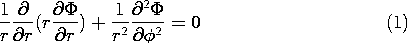

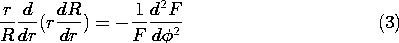


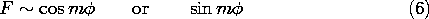





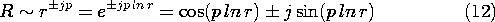


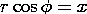


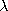 l situated at the origin, the charge
+
l situated at the origin, the charge
+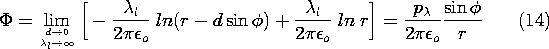


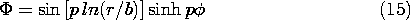


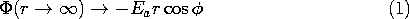
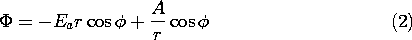

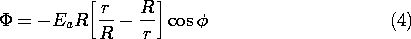

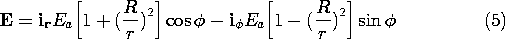
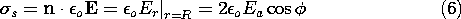

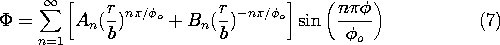
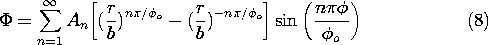
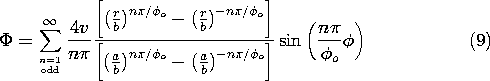
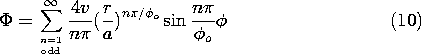

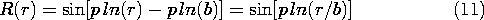
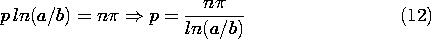
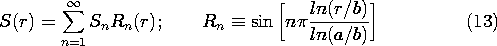

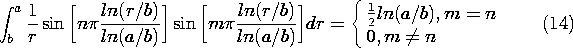

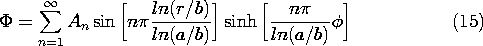
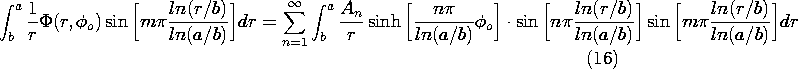
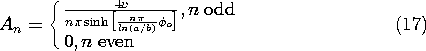
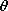 . These two-dimensional
solutions therefore satisfy boundary conditions
on spheres and cones.
. These two-dimensional
solutions therefore satisfy boundary conditions
on spheres and cones.

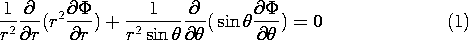



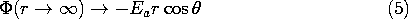
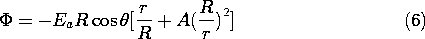
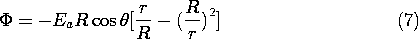
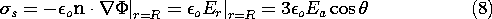



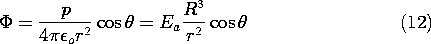
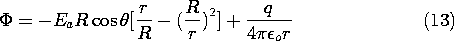
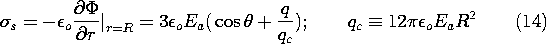



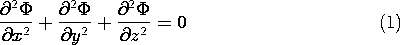

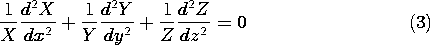
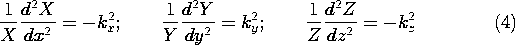

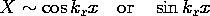
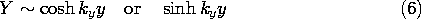

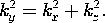
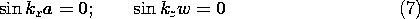
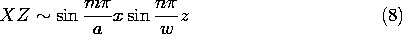
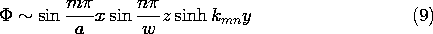
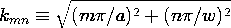
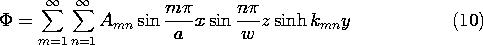

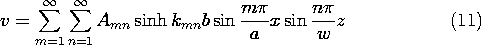
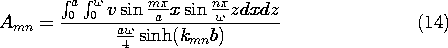
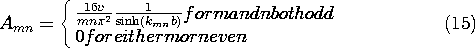
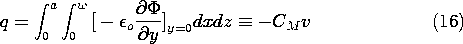
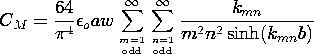

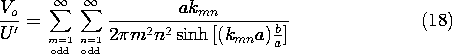
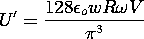
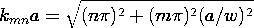
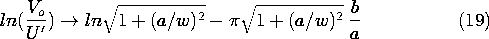

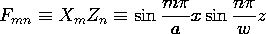

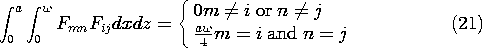



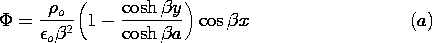


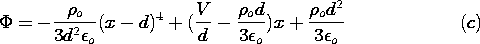
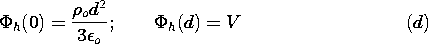


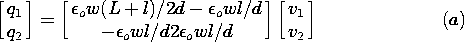




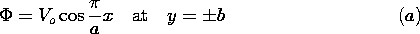
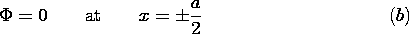
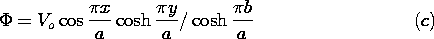


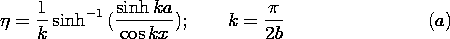
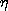 is as shown in Fig. P5.4.5.
is as shown in Fig. P5.4.5.
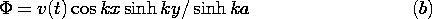
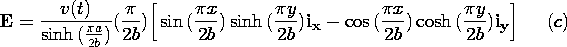
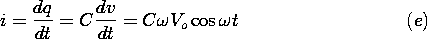
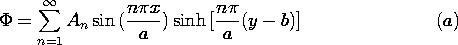
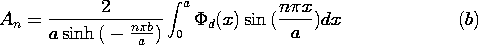


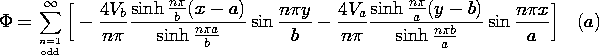
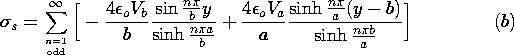



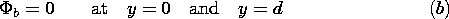
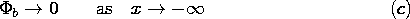
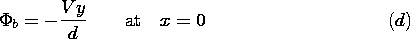
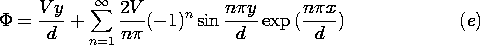


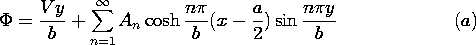

 x). Show that
x). Show that