The previous chapters postulated surface charge densities that appear and disappear as required by the boundary conditions obeyed by surfaces of conductors. Thus, the idea that the distribution of the charge density may be linked to the field it induces is not new. Thus far, however, no consideration has been given in any detail to the physical laws which determine the occurrence and behavior of charge densities in matter.
To set the stage for this and the next chapter, consider two possible pictures that could be used to explain why an object distorts an initially uniform electric field. In Fig. 6.0.1a, the sphere is composed of a metallic conductor, and therefore composed of atoms having electrons that are free to move from one atomic site to another. Suppose, to begin with, that there are equal numbers of positive sites and negative electrons. In the absence of an applied field and on a scale that is large compared to the distance between atoms (that is, on a macroscopic scale), there is therefore no charge density at any point within the material.
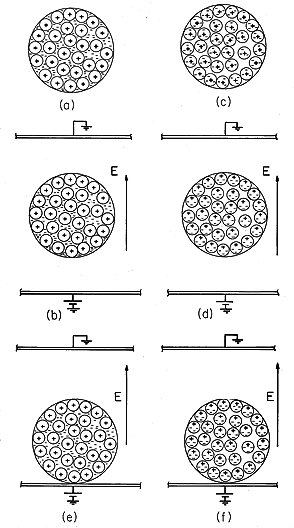
Figure 6.0.1 In the left-hand sequence, the sphere is conducting, while on the right, it is polarizable and not conducting. When this object is placed in an initially uniform electric field, the electrons are subject to forces that tend to make them concentrate on the south pole of the sphere. This requires only that the electrons migrate downward slightly (on the average, less than an interatomic distance). Because the interior of the sphere must be field free in the final equilibrium (steady) state, the charge density remains zero at each point within the volume of the material. However, to preserve a zero net charge, the positive atomic sites on the north pole of the sphere are uncovered. After a time, the net result is the distribution of surface charge density shown in Fig. 6.0.1b. [In fact, provided the electrodes are well-removed from the sphere, this is the distribution found in Example 5.9.1.]
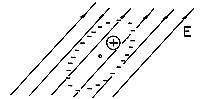
Now consider an alternative picture of the physics that can lead to a very similar result. As shown in Fig. 6.0.1c, the material is composed of atoms, molecules, or groups of molecules (domains) in which the electric field induces dipole moments. For example, suppose that the dipole moments are of an atomic scale and, in the absence of an electric field, do not exist; the moments are induced because atoms contain positively charged nuclei and electrons orbiting around the nuclei. According to quantum theory, electrons orbiting the nuclei are not to be viewed as localized at any particular instant of time. It is more appropriate to think of the electrons as "clouds" of charge surrounding the nuclei. Because the charge of the orbiting electrons is equal and opposite to the charge of the nuclei, a neutral atom has no net charge. An atom with no permanent dipole moment has the further property that the center of the negative charge of the electron "clouds" coincides with the center of the positive charge of the nuclei. In the presence of an electric field, the center of positive charge is pulled in the direction of the field while the center of negative charge is pushed in the opposite direction. At the atomic level, this relative displacement of charge centers is as sketched in Fig. 6.0.2. Because the two centers of charge no longer coincide, the particle acquires a dipole moment. We can represent each atom by a pair of charges of equal magnitude and opposite sign separated by a distance d.
Figure 6.0.2 Nucleus with surrounding electronic charge cloud displaced by applied electric field. On the macroscopic scale of the sphere and in an applied field, the dipoles then appear somewhat as shown in Fig. 6.0.1d. In the interior of the sphere, the polarization leaves each positive charge in the vicinity of a negative one, and hence there is no net charge density. However, at the north pole there are no negative charges to neutralize the positive ones, and at the south pole no positive ones to pair up with the negative ones. The result is a distribution of surface charge density that does not differ qualitatively from that for the metal sphere.
How can we distinguish between these two very different situations? Suppose that the two spheres make contact with the lower electrode, as shown in parts (e) and (f) of the figure. By this we mean that in the case of the metal sphere, electrons are now free to pass between the sphere and the electrode. Once again, electrons move slightly downward, leaving positive sites exposed at the top of the sphere. However, some of those at the bottom flow into the lower electrode, thus reducing the amount of negative surface charge on the lower side of the metal sphere.
At the top, the polarized sphere shown by Fig. 6.0.1f has a similar distribution of positive surface charge density. But one very important difference between the two situations is apparent. On an atomic scale in the ideal dielectric, the orbiting electrons are paired with the parent atom, and hence the sphere must remain neutral. Thus, the metallic sphere now has a net charge, while the one made up of dipoles does not.
Experimental evidence that a metallic sphere had indeed acquired a net charge could be gained in a number of different ways. Two are clear from demonstrations in Chap. 1. A pair of spheres, each charged by "induction" in this fashion, would repel each other, and this could be demonstrated by the experiment in Fig. 1.3.10. The charge could also be measured by charge conservation, as in Demonstration 1.5.1. Presumably, the same experiments carried out using insulating spheres would demonstrate the existence of no net charge.
Because charge accumulations occur via displacements of paired charges (polarization) as well as of charges that can move far away from their partners of opposite sign, it is often appropriate to distinguish between these by separating the total charge density
into parts
In this chapter, we consider insulating materials and therefore focus on the effects of the paired or polarization charge density. Additional effects of unpaired charges are taken up in the next chapter.
Our first step, in Sec. 6.1, is to relate the polarization charge density to the density of dipoles- to the polarization density. We do this because it is the polarization density that can be most easily specified. Sections 6.2 and 6.3 then focus on the first of two general classes of polarization. In these sections, the polarization density is permanent and therefore specified without regard for the electric field. In Sec. 6.4, we discuss simple constitutive laws expressing the action of the field upon the polarization. This field-induced atomic polarization just described is typical of physical situations. The field action on the atom, molecule, or domain is accompanied by a reaction of the dipoles on the field that must be considered simultaneously. That is, within such a polarizable body placed into an electric field, a polarization charge density is produced which, in turn, modifies the electric field. In Secs. 6.5-6.7, we shall study methods by which self-consistent solutions to such problems are obtained.
