7.0
Introduction

This is the last in the sequence of chapters concerned largely with electrostatic and electroquasistatic fields. The electric field E is still irrotational and can therefore be represented in terms of the electric potential .

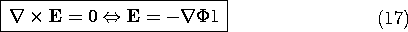
The source of E is the charge density. In Chap. 4, we began our exploration of EQS fields by treating the distribution of this source as prescribed. By the end of Chap. 4, we identified solutions to boundary value problems, where equipotential surfaces were replaced by perfectly conducting metallic electrodes. There, and throughout Chap. 5, the sources residing on the surfaces of electrodes as surface charge densities were made self-consistent with the field. However, in the volume, the charge density was still prescribed.

In Chap. 6, the first of two steps were taken toward a self-consistent description of the charge density in the volume. In relating E to its sources through Gauss' law, we recognized the existence of two types of charge densities, _u and _p, which, respectively, represented unpaired and paired charges. The paired charges were related to the polarization density P with the result that Gauss' law could be written as (6.2.15)

where D _o E + P. Throughout Chap. 6, the volume was assumed to be perfectly insulating. Thus, _p was either zero or a given distribution. The second step toward a self-consistent description of the volume charge density is taken by adding to (1) and (2) an equation expressing conservation of the unpaired charges, (2.3.3).

That the charge appearing in this equation is indeed the unpaired charge density follows by taking the divergence of Ampère's law expressed with polarization, (6.2.17), and using Gauss' law as given by (2) to eliminate D.

To make use of these three differential laws, it is necessary to specify P and J. In Chap. 6, we learned that the former was usually accomplished by either specifying the polarization density P or by introducing a polarization constitutive law relating P to E. In this chapter, we will almost always be concerned with linear dielectrics, where D = E.

A new constitutive law is required to relate J_u to the electric field intensity. The first of the following sections is therefore devoted to the constitutive law of conduction. With the completion of Sec. 7.1, we have before us the differential laws that are the theme of this chapter.

Figure 7.0.1 EQS distributions of potential and current density are analogous to those of voltage and current in a network of resistors and capacitors. (a) Systems of perfect dielectrics and perfect conductors are analogous to capacitive networks. (b) Conduction effects considered in this chapter are analogous to those introduced by adding resistors to the network.

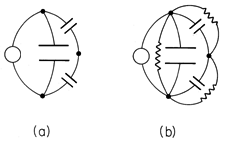
To anticipate the developments that follow, it is helpful to make an analogy to circuit theory. If the previous two chapters are regarded as describing circuits consisting of interconnected capacitors, as shown in Fig. 7.0.1a, then this chapter adds resistors to the circuit, as in Fig. 7.0.1b. Suppose that the voltage source is a step function. As the circuit is composed of resistors and capacitors, the distribution of currents and voltages in the circuit is finally determined by the resistors alone. That is, as t 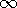, the capacitors cease charging and are equivalent to open circuits. The distribution of voltages is then determined by the steady flow of current through the resistors. In this long-time limit, the charge on the capacitors is determined from the voltages already specified by the resistive network.

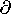The steady current flow is analogous to the field situation where _u / t 0 in the conservation of charge expression, (3). We will find that (1) and (3), the latter written with J_u represented by the conduction constitutive law, then fully determine the distribution of potential, of E, and hence of J_u. Just as the charges on the capacitors in the circuit of Fig. 7.0.1b are then specified by the already determined voltage distribution, the charge distribution can be found in an after-the-fact fashion from the already determined field distribution by using Gauss' law, (2). After considering the physical basis for common conduction constitutive laws in Sec. 7.1, Secs. 7.2-7.6 are devoted to steady conduction phenomena.

In the circuit of Fig. 7.0.1b, the distribution of voltages an instant after the voltage step is applied is determined by the capacitors without regard for the resistors. From a field theory point of view, this is the physical situation described in Chaps. 4 and 5. It is the objective of Secs. 7.7-7.9 to form an appreciation for how this initial distribution of the fields and sources relaxes to the steady condition, already studied in Secs. 7.2-7.6, that prevails when t .

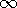In Chaps. 3-5 we invoked the "perfect conductivity" model for a conductor. For electroquasistatic systems, we will conclude this chapter with an answer to the question, "Under what circumstances can a conductor be regarded as perfect?"

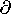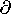Finally, if the fields and currents are essentially static, there is no distinction between EQS and MQS laws. That is, if B/ t is negligible in an MQS system, Faraday's law again reduces to (1). Thus, the first half of this chapter provides an understanding of steady conduction in some MQS as well as EQS systems. In Chap. 8, we determine the magnetic field intensity from a given distribution of current density. Provided that rates of change are slow enough so that effects of magnetic induction can be ignored, the solution to the steady conduction problem as addressed in Secs. 7.2-7.6 provides the distribution of the magnetic field source, the current density, needed to begin Chap. 8.

Just how fast can the fields vary without producing effects of magnetic induction? For EQS systems, the answer to this question comes in Secs. 7.7-7.9. The EQS effects of finite conductivity and finite rates of change are in sharp contrast to their MQS counterparts, studied in the last half of Chap. 10.