7.8
Electroquasistatic Conduction Laws forInhomogeneous Materials

In this section, we extend the discussion of transients to situations in which the electrical permittivity and Ohmic conductivity are arbitrary functions of space.

Distributions of these parameters, as exemplified in Figs. 6.5.1 and 7.2.3, might be uniform, piece-wise uniform, or smoothly nonuniform. The specific examples falling into these categories answer three questions.

tend to accumulate when it disappears from a region having uniform properties.

(a)	Where does the unpaired charge density, found in Sec. 7.7,
(b)	With the unpaired charge density determined by the self-consistent EQS laws, what is the equation governing the potential distribution throughout the volume of interest?
(c)	What boundary and initial conditions make the solutions to this equation unique?

The laws studied in this section and exemplified in the next describe both the perfectly insulating limit of Chap. 6 and the conduction dominated limit of Secs. 7.1-7.6. More important, as suggested in Sec. 7.0, they describe how these limiting situations are related in EQS systems.

Evolution of Unpaired Charge Density

With a nonuniform conductivity distribution, the statement of charge conservation and Ohm's law expressed by (7.7.1) becomes

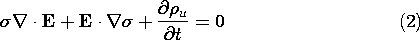
Similarly, with a nonuniform permittivity, Gauss' law as given by (7.7.2) becomes

Elimination of 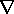E between these equations gives an expression that is the generalization of the charge relaxation equation, (7.7.3).

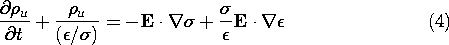
Wherever the electric field has a component in the direction of a gradient of or , the unpaired charge density can be present and can be temporally increasing or decreasing. If a steady state has been established, in the sense that time rates of change are negligible, the charge distribution is given by (4), because then, 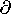_u /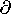 t = 0. Note that this is the distribution of (7.2.8) that prevails for steady conduction. We can therefore expect that the charge density found to disappear from a region of uniform properties in Sec. 7.7 will reappear at surfaces of discontinuity of and or in regions where and vary smoothly.

Electroquasistatic Potential Distribution

To evaluate (4), the self-consistent electric field intensity is required. With the objective of determining that field, Gauss' law, (7.7.2), is used to eliminate _u from the charge conservation statement, (7.7.1).

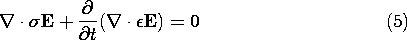
For the first time in the analysis of charge relaxation, we now introduce the electroquasistatic approximation

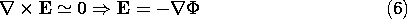
and (5) becomes the desired expression governing the evolution of the electric potential.

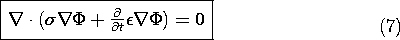
Uniqueness

Consider now the initial and boundary conditions that make solutions to (7) unique. Suppose that throughout the volume V, the initial charge distribution is given as

and that on the surface S enclosing this volume, the potential is a given function of time

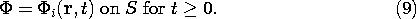
Thus, when t = 0, the initial distribution of electric field intensity satisfies Gauss' law. The initial potential distribution satisfies the same law as for regions occupied by perfect dielectrics.

Given the boundary condition of (9) when t = 0, it follows from Sec. 5.2 that the initial distribution of potential is uniquely determined.

Is the subsequent evolution of the field uniquely determined by (7) and the initial and boundary conditions? To answer this question, we will take a somewhat more formal approach than used in Sec. 5.2 but nevertheless use the same reasoning. Supose that there are two solutions, = _a and = _b, that satisfy (7) and the same initial and boundary conditions.

Equation (7) is written first with = _a and then with = _b. With _{d a} - _b, the difference between these two equations becomes

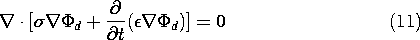
Multiplication of (11) by _d and integration over the volume V gives

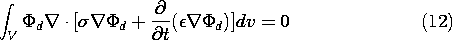
The objective in the following manipulation is to turn this integration either into one over positive definite quantities or into an integration over the surface S, where the boundary conditions determine the potential. The latter is achieved if the integrand can be expressed as a divergence. Thus, the vector identity

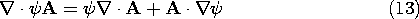
is used to write (12) as

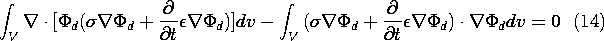
and then Gauss' theorem converts the first integral to one over the surface S enclosing V.

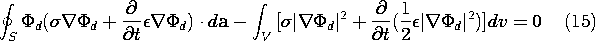
The conversion of (12) to (15) is an example of a three-dimensional integration by parts. The surface integral is analogous to an evaluation at the endpoints of a one-dimensional integral.

If both _a and _b satisfy the same condition on S, namely (9), then the difference potential is zero on S for all 0 t. Thus, the surface integral in (15) vanishes. We are left with the requirement that for 0 t,

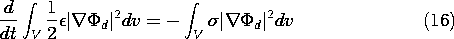
Because both _a and _b satisfy the same initial conditions, _d must initially be zero. Thus, for _d to change to a nonzero value from zero, the derivative on the left must be positive. However, the integral on the right can only be zero or negative. Thus, _d must stay zero for all time. We conclude that the fields found using (7), the initial condition of (8), and boundary conditions of (9) are unique.