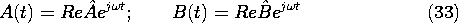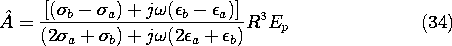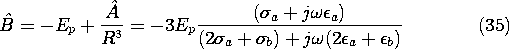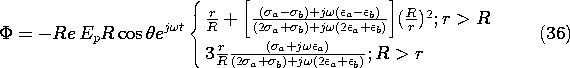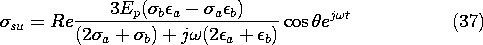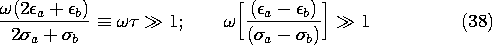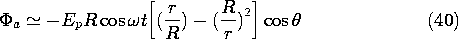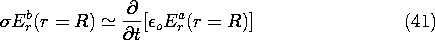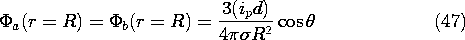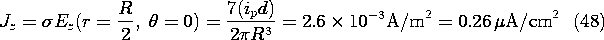7
Conduction and
Electroquasistatic
Charge Relaxation
7.0 Introduction
This is the last in the sequence of chapters concerned largely
with electrostatic and electroquasistatic fields. The
electric field E is still irrotational and can therefore be
represented in terms of the electric potential  .
.
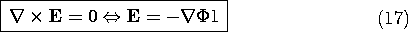
The source of E is the charge density. In Chap. 4, we began
our exploration of EQS fields by treating the distribution of this
source as prescribed. By the end of Chap. 4, we identified
solutions to boundary value problems, where equipotential surfaces
were replaced by perfectly conducting metallic electrodes. There, and
throughout Chap. 5, the sources residing on the surfaces
of electrodes as surface charge densities were made self-consistent
with the field. However, in the volume, the charge density was still
prescribed.
In Chap. 6, the first of two steps were taken toward a self-consistent
description of the charge density in the volume.
In relating E to its sources through Gauss' law, we recognized
the existence of two types of charge densities,  u and
u and
 p, which, respectively, represented unpaired and paired charges.
The paired charges were related to the polarization density P
with the result that Gauss' law could be written as (6.2.15)
p, which, respectively, represented unpaired and paired charges.
The paired charges were related to the polarization density P
with the result that Gauss' law could be written as (6.2.15)

where D \equiv  o E + P. Throughout Chap. 6, the volume
was assumed to be perfectly insulating. Thus,
o E + P. Throughout Chap. 6, the volume
was assumed to be perfectly insulating. Thus,  p was either
zero or a given distribution.
The second step toward a self-consistent description of the
volume charge density is taken by adding to (1) and (2) an equation
expressing conservation of the unpaired charges, (2.3.3).
p was either
zero or a given distribution.
The second step toward a self-consistent description of the
volume charge density is taken by adding to (1) and (2) an equation
expressing conservation of the unpaired charges, (2.3.3).

That the charge appearing in this equation is indeed the unpaired
charge density follows by taking the divergence of Ampère's law
expressed with polarization, (6.2.17), and using Gauss' law as given
by (2) to eliminate D.
To make use of these three differential laws, it is necessary to
specify P and J. In Chap. 6, we learned that the former was
usually accomplished by either specifying the polarization density
P or by introducing a polarization constitutive law relating
P to E. In this chapter, we will almost always be concerned
with linear dielectrics, where D =  E.
E.
A new constitutive law is required to relate Ju to the electric
field intensity. The first of the following sections is therefore
devoted to the constitutive law of conduction. With the completion
of Sec. 7.1, we have before us the differential laws that are the
theme of this chapter.

To anticipate the developments that follow, it is helpful to make
an analogy to circuit theory. If the previous two chapters are
regarded as describing circuits consisting of
interconnected capacitors, as shown in Fig. 7.0.1a, then this chapter
adds resistors to the circuit, as in Fig. 7.0.1b. Suppose that the
voltage source is a step function. As the circuit is composed of
resistors and capacitors, the distribution of currents and voltages in
the circuit is finally determined by the resistors alone. That is,
as t 
 , the capacitors cease charging and are
equivalent to open circuits. The distribution of voltages is then
determined by the steady flow of current through the resistors. In
this long-time limit, the charge on the capacitors is determined from
the voltages already specified by the resistive network.
, the capacitors cease charging and are
equivalent to open circuits. The distribution of voltages is then
determined by the steady flow of current through the resistors. In
this long-time limit, the charge on the capacitors is determined from
the voltages already specified by the resistive network.
The steady current flow is analogous to the field
situation where 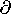
 u /
u /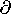 t\
t\  0 in the
conservation of
charge expression, (3). We will find that (1) and (3), the latter
written with Ju represented by the conduction constitutive
law, then fully determine the distribution of potential, of E, and
hence of Ju. Just as the charges on the capacitors in the
circuit of Fig. 7.0.1b are then specified by the already determined
voltage distribution, the charge distribution can be found in an
after-the-fact fashion from the already determined field distribution
by using Gauss' law, (2). After considering the physical basis for
common conduction constitutive laws in Sec. 7.1, Secs. 7.2-7.6 are
devoted to steady conduction phenomena.
0 in the
conservation of
charge expression, (3). We will find that (1) and (3), the latter
written with Ju represented by the conduction constitutive
law, then fully determine the distribution of potential, of E, and
hence of Ju. Just as the charges on the capacitors in the
circuit of Fig. 7.0.1b are then specified by the already determined
voltage distribution, the charge distribution can be found in an
after-the-fact fashion from the already determined field distribution
by using Gauss' law, (2). After considering the physical basis for
common conduction constitutive laws in Sec. 7.1, Secs. 7.2-7.6 are
devoted to steady conduction phenomena.
In the circuit of Fig. 7.0.1b, the distribution of voltages an
instant after the voltage step is applied is determined by the
capacitors without regard for the resistors. From a field theory
point of view, this is the physical situation described in Chaps. 4
and 5. It is the objective of Secs. 7.7-7.9 to form an appreciation
for how this initial distribution of the fields and sources relaxes to
the steady condition, already studied in Secs. 7.2-7.6, that prevails
when t 
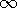 .
.
In Chaps. 3-5 we invoked the "perfect conductivity" model for
a conductor. For electroquasistatic systems, we will
conclude this chapter with an answer to the question, "Under what
circumstances can a conductor be regarded as perfect?"
Finally, if the fields and currents are essentially static, there
is no distinction between EQS and MQS laws. That is, if 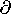 B/
B/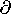 t is negligible in an MQS system, Faraday's law again reduces to
(1). Thus, the first half of this chapter provides an understanding
of steady conduction in some MQS as well as EQS systems. In Chap. 8,
we determine the
magnetic field intensity from a given distribution of current
density. Provided that rates of change are slow enough so that
effects of magnetic induction can be ignored, the solution to the
steady conduction problem as addressed in Secs. 7.2-7.6 provides the
distribution of the magnetic field source, the current density,
needed to begin Chap. 8.
t is negligible in an MQS system, Faraday's law again reduces to
(1). Thus, the first half of this chapter provides an understanding
of steady conduction in some MQS as well as EQS systems. In Chap. 8,
we determine the
magnetic field intensity from a given distribution of current
density. Provided that rates of change are slow enough so that
effects of magnetic induction can be ignored, the solution to the
steady conduction problem as addressed in Secs. 7.2-7.6 provides the
distribution of the magnetic field source, the current density,
needed to begin Chap. 8.
Just how fast can the fields vary without producing effects of
magnetic induction? For EQS systems, the answer to this
question comes in Secs. 7.7-7.9. The EQS effects of finite
conductivity and finite rates of change are in sharp contrast to
their MQS counterparts, studied in the last half of Chap. 10.
7.1 Conduction Constitutive Laws
In the presence of materials, fields vary in space over at least
two length scales. The microscopic scale is typically the distance
between atoms or molecules while the much larger macroscopic
scale is typically the dimension of an object made from the
material. As developed in the previous chapter, fields in polarized
media are averages over the microscopic scale of the dipoles. In
effect, the experimental determination of the polarization
constitutive law relating the macroscopic P and E (Sec. 6.4)
does not deal with the microscopic field.
With the understanding that experimentally measured values will
again be used to evaluate macroscopic parameters, we assume
that the average force acting on an unpaired or free charge, q,
within matter is of the same form as the Lorentz force, (1.1.1).

By contrast with a polarization charge, a free
charge is not bound to the atoms and molecules, of which matter is
constituted, but under the influence of the electric and magnetic
fields can travel over distances that are large compared to
interatomic or intermolecular distances. In general, the charged
particles collide with the atomic or molecular constituents, and so
the force given by (1) does not lead to uniform acceleration, as it
would for a charged particle in free space. In fact, in the
conventional conduction process, a particle experiences so many
collisions on time scales of interest that the average velocity it
acquires is quite low. This phenomenon gives rise to two
consequences. First, inertial
effects can be disregarded in the time average balance of forces on
the particle. Second, the velocity is so low that the forces due to
magnetic fields are usually negligible. (The
magnetic force term leads to the Hall effect, which is small and very
difficult to observe in metallic conductors, but because of the
relatively larger translational velocities reached by the charge
carriers in semiconductors, more easily observed in these.)
With the driving force ascribed solely to the electric field and
counterbalanced by a "viscous" force, proportional to the average
translational velocity v of the charged particle, the force equation
becomes

where the upper and lower signs correspond to particles of positive
and negative charge, respectively. The coefficients  \pm
are positive
constants representing the time average "drag" resulting from
collisions of the carriers with the fixed atoms or molecules through
which they move.
\pm
are positive
constants representing the time average "drag" resulting from
collisions of the carriers with the fixed atoms or molecules through
which they move.
Written in terms of the mobilities, 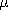 \pm,
the velocities of the positive and negative particles follow from
(2) as
\pm,
the velocities of the positive and negative particles follow from
(2) as

where 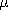 \pm = |q\pm |/
\pm = |q\pm |/ \pm.
The mobility is defined as positive. The positive and negative
particles move with and against the electric field intensity,
respectively.
\pm.
The mobility is defined as positive. The positive and negative
particles move with and against the electric field intensity,
respectively.
Now suppose that there are two types of charged particles, one
positive and the other negative. These might be the positive sodium
and negative chlorine ions resulting when salt is dissolved in water.
In a metal, the positive charges represent the (zero mobility) atomic
sites, while the negative particles are electrons. Then, with N+ and
N-, respectively, defined as the number of these charged particles per
unit volume, the current density is
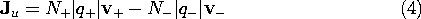
A flux of negative particles comprises an electrical current that is
in a direction opposite to that of the particle motion. Thus, the
second term in (4) appears with a negative sign. The velocities in
this expression are related to E by (3), so it follows that the
current density is
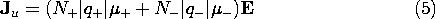
In terms of the same variables, the unpaired charge density is

Ohmic Conduction
In general, the distributions of particle densities N+ and N-
are determined by the electric field. However, in many materials, the
quantity in brackets in (5) is a property of the material, called
the electrical conductivity  .
.
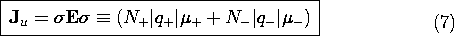
The MKS units of  are (ohm - m)-1 \equiv Siemens/m =
S/m.
are (ohm - m)-1 \equiv Siemens/m =
S/m.
In these materials, the charge densities N+ q+ and N- q-
keep each other in (approximate) balance so that there is little
effect of the applied field on their sum. Thus, the conductivity
 (r) is specified as a function of position in nonuniform
media by the distribution N\pm in the material and by the local
mobilities, which can also be functions of r.
(r) is specified as a function of position in nonuniform
media by the distribution N\pm in the material and by the local
mobilities, which can also be functions of r.
The conduction constitutive law given by (7) is Ohm's law
generalized in a field-theoretical sense. Values of the conductivity
for some common materials are given in Table 7.1.1. It is important
to keep in mind that any constitutive law is of restricted use, and
Ohm's law is no exception. For metals and semiconductors, it is
usually a good model on a sufficiently large scale. It is also
widely used in dealing with electrolytes. However, as materials
become semi-insulators, it can be of questionable validity.

Unipolar Conduction
To form an appreciation for the implications of Ohm's
law, it will be helpful to contrast it with the law for unipolar
conduction. In that case, charged particles of only one sign move in
a neutral background, so that the expressions for the current density
and charge density that replace (5) and (6) are


where the charge density  now carries its own sign. Typical of
situations described by these relations is the passage of ions through
air.
now carries its own sign. Typical of
situations described by these relations is the passage of ions through
air.
Note that a current density exists in unipolar conduction only if
there is a net charge density. By contrast, for Ohmic conduction,
where the current density and the charge density are given by (7)
and (6), respectively, there can be a current density at a location where
there is no net charge density. For example, in a metal, negative
electrons move through a background of fixed positively charged atoms.
Thus, in (7), 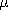 + = 0 and the conductivity is due solely to the
electrons. But it follows from (6) that the positive charges do have
an important effect, in that they can nullify the charge density of
the electrons. We will often find that in an Ohmic conductor there is
a current density where there is no net unpaired charge density.
+ = 0 and the conductivity is due solely to the
electrons. But it follows from (6) that the positive charges do have
an important effect, in that they can nullify the charge density of
the electrons. We will often find that in an Ohmic conductor there is
a current density where there is no net unpaired charge density.
7.2 Steady Ohmic Conduction
To set the stage for the next two sections, consider the fields
in a material that has a linear polarizability and is described by
Ohm's law, (7.1.7).
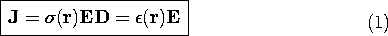
In general, these properties are functions of position, r.
Typically, electrodes are used to constrain the potential over some of
the surface enclosing this material, as suggested by Fig. 7.2.1.

In this section, we suppose that the excitations are essentially
constant in time, in the sense that the rate of accumulation of
charge at any
given location has a negligible influence on the distribution of the
current density. Thus, the time derivative of the unpaired charge
density in the charge conservation law, (7.0.3), is negligible.
This implies that the current density is solenoidal.

Of course, in the EQS approximation, the electric field is also
irrotational.
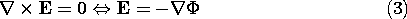
Combining (2) and (3) gives a second-order differential equation
for the potential distribution.

In regions of uniform conductivity ( = constant), it assumes
a familiar form.
= constant), it assumes
a familiar form.

In a uniform conductor, the potential distribution satisfies Laplace's
equation.
It is important to realize that the physical reasons for
obtaining Laplace's equation for the potential distribution in a
uniform conductor are quite different from those that led to Laplace's
equation in the electroquasistatic cases of Chaps. 4 and 5. With
steady conduction, the governing requirement is that the divergence of
the current density vanish. The unpaired charge density does not
influence the current distribution, but is rather determined by it.
In a uniform conductor, the continuity constraint on J happens to
imply that there is no unpaired charge density.
In a nonuniform conductor, (4) shows that there is an
accumulation of unpaired charge. Indeed, with  a function of
position, (2) becomes
a function of
position, (2) becomes

Once the potential distribution has been found, Gauss' law can be
used to determine the distribution of unpaired charge density.

Equation (6) can be solved for div E and that quantity
substituted into (7) to obtain
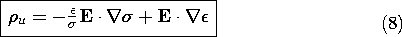
Even though the distribution of  plays no part in determining
E, through Gauss' law, it does influence the distribution of
unpaired charge density.
plays no part in determining
E, through Gauss' law, it does influence the distribution of
unpaired charge density.
Continuity Conditions
Where the conductivity changes abruptly, the continuity conditions
follow from (2) and (3). The condition

is derived from (2), just as (1.3.17) followed from Gauss' law. The
continuity conditions implied by (3) are familiar from Sec. 5.3.
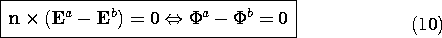
Illustration. Boundary Condition at an Insulating Surface
Insulated wires and ordinary resistors are examples where a
conducting medium is bounded by one that is essentially insulating.
What boundary condition should be used to determine the
current distribution inside the conducting material?

In Fig. 7.2.2, region (a) is relatively insulating compared to
region (b),  a \ll
a \ll  b.
It follows from (9) that the normal electric
field in region (a) is much greater than in region (b), Ena \gg
Enb. According to (10), the tangential components of E are
equal, Eta = Etb. With the assumption that the normal and
tangential components of E are of the same order of magnitude
in the insulating region, these two statements establish the relative
magnitudes of the normal and tangential components of E,
respectively, sketched in Fig.
7.2.2. We conclude that in the relatively conducting region (b), the
normal component of E is essentially zero compared to the
tangential component. Thus, to determine the fields in the relatively
conducting region, the boundary condition used
at an insulating surface is
b.
It follows from (9) that the normal electric
field in region (a) is much greater than in region (b), Ena \gg
Enb. According to (10), the tangential components of E are
equal, Eta = Etb. With the assumption that the normal and
tangential components of E are of the same order of magnitude
in the insulating region, these two statements establish the relative
magnitudes of the normal and tangential components of E,
respectively, sketched in Fig.
7.2.2. We conclude that in the relatively conducting region (b), the
normal component of E is essentially zero compared to the
tangential component. Thus, to determine the fields in the relatively
conducting region, the boundary condition used
at an insulating surface is
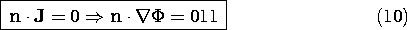
At an insulating boundary, inside the conductor, the normal
derivative of the potential is zero, while the boundary potential
adjusts itself to make this true. Current lines are diverted so
that they remain tangential to the insulating boundary, as sketched in
Fig. 7.2.2.
Just as Gauss' law embodied in (8) is used to find the unpaired
volume charge density ex post facto, Gauss' continuity
condition (6.5.3) serves to evaluate the unpaired surface charge
density. Combined with the current continuity condition, (9), it
becomes
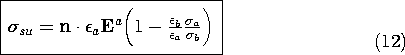
Conductance
If there are only two electrodes contacting the conductor
of Fig. 7.2.1 and hence one voltage v1 = v and current i1 = i,
the voltage-current relation for the terminal pair is of the form

where G is the conductance. To relate G to field quantities, (2) is
integrated over a volume V enclosed by a surface S, and Gauss' theorem
is used to convert the volume integral to one of the current  E
E  da over
the surface S. This integral law is then applied to the surface shown
in Fig. 7.2.1 enclosing the electrode that is connected to the
positive terminal. Where it intersects the wire, the contribution is
-i, so that the integral over the closed surface becomes
da over
the surface S. This integral law is then applied to the surface shown
in Fig. 7.2.1 enclosing the electrode that is connected to the
positive terminal. Where it intersects the wire, the contribution is
-i, so that the integral over the closed surface becomes

where S1 is the surface where the perfectly conducting electrode
having potential v1 interfaces with the Ohmic conductor.
Division of (14) by the terminal voltage v gives an expression
for the conductance defined by (13).
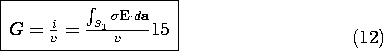
Note that the linearity of the equation governing the potential
distribution, (4), assures that i is proportional to v. Hence,
(15) is independent of v and, indeed, a parameter characterizing the
system independent of the excitation.
A comparison of (15) for the conductance with (6.5.6) for the
capacitance suggests an analogy that will be developed in Sec. 7.5.
Qualitative View of Fields in Conductors
Three classes of steady
conduction configurations are typified in Fig. 7.2.3. In the first,
the region of interest is one of uniform conductivity bounded either
by surfaces with constrained potentials or by perfect insulators. In the
second, the conductivity varies abruptly but by a finite amount at
interfaces, while in the third, it varies smoothly. Because Gauss' law
plays no role in determining the potential distribution, the
permittivity distributions in these three classes of configurations
are arbitrary. Of course, they do have a strong influence on the
resulting distributions of unpaired charge density.

A qualitative picture of the electric field distribution within
conductors emerges from arguments similar to those used in Sec. 6.5
for linear dielectrics. Because J is solenoidal and has the same
direction as E, it passes from the high-potential to the
low-potential electrodes through tubes within which lines of J
neither terminate nor originate. The
E lines form the same tubes but either terminate or originate on
the sum of unpaired and polarization charges. The sum of these charge
densities is div  o E, which can be
determined from (6).
o E, which can be
determined from (6).
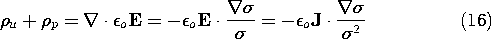
At an abrupt discontinuity, the sum of the surface charges determines
the discontinuity of normal E. In view of (9),
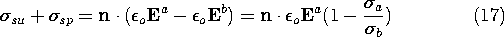
Note that the distribution of  plays no part in shaping the
E lines.
plays no part in shaping the
E lines.
In following a typical current tube from high potential to low in
the uniform conductor of Fig. 7.2.3a, no conductivity gradients are
encountered, so (16) tells us there is no source of E. Thus,
it is no surprise that  satisfies Laplace's equation throughout
the uniform conductor.
satisfies Laplace's equation throughout
the uniform conductor.
In following the current tube through the discontinuity
of Fig. 7.2.3b, from low to high conductivity, (17) shows that there
is a negative surface source of E. Thus, E tends to be
excluded from the more conducting region and intensified in the less
conducting region.
With the conductivity increasing smoothly in the direction of
E, as illustrated in Fig. 7.2.3c, E 
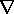
 is
positive. Thus, the source of E is negative and the E
lines attenuate along the flux tube.
is
positive. Thus, the source of E is negative and the E
lines attenuate along the flux tube.
Uniform and piece-wise uniform conductors are commonly
encountered, and examples in this category are taken up in Secs. 7.4
and 7.5. Examples where the conductivity is smoothly distributed are
analogous to the smoothly varying permittivity configurations
exemplified in Sec. 6.7. In a simple one-dimensional configuration,
the following example illustrates all three categories.
Example 7.2.1. One-Dimensional Resistors
The resistor shown in Fig. 7.2.4 has a uniform cross-section of
area A in any x - z plane. Over its length d it has a
conductivity  (y). Perfectly conducting electrodes constrain
the potential to be v
at y = 0 and to be zero at y = d. The cylindrical conductor is
surrounded by a perfect insulator.
(y). Perfectly conducting electrodes constrain
the potential to be v
at y = 0 and to be zero at y = d. The cylindrical conductor is
surrounded by a perfect insulator.

The potential is assumed to depend only on y. Thus, the electric
field and current density are y directed, and the condition that
there be no component of E normal to the insulating boundaries
is automatically satisfied. For the one-dimensional field, (4)
reduces to

The quantity in parentheses, the negative of the current density, is
conserved over the length of the resistor. Thus, with Jo defined as
constant,

This expression is now integrated from the lower electrode to an
arbitrary location y.
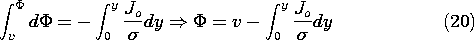
Evaluation of this expression where y = d and  = 0 relates
the current density to the terminal voltage.
= 0 relates
the current density to the terminal voltage.
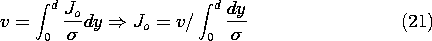
Introduction of this expression into (20) then gives the potential
distribution.
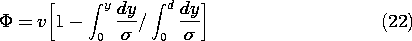
The conductance, defined by (15), follows from (21).

These relations hold for any one-dimensional distribution of  .
Of course, there is no dependence on
.
Of course, there is no dependence on  , which could have
any distribution. The permittivity could even depend on x and z.
In terms of the
circuit analogy suggested in the introduction, the resistors determine
the distribution of voltages regardless of the interconnected
capacitors.
, which could have
any distribution. The permittivity could even depend on x and z.
In terms of the
circuit analogy suggested in the introduction, the resistors determine
the distribution of voltages regardless of the interconnected
capacitors.
Three special cases conform to the three categories of
configurations illustrated in Fig. 7.2.3.
Uniform Conductivity
If  is uniform, evaluation of (22) and (23) gives
is uniform, evaluation of (22) and (23) gives


The potential and electric field are the same as they would be between
plane parallel electrodes in free space in a uniform perfect
dielectric. However, because of the insulating walls, the conduction
field remains uniform regardless of the length of the resistor
compared to its transverse dimensions.
It is clear from (16) that there is no volume charge density, and
this is consistent with the uniform field that has been found. These
distributions of  ,
,  , and E are shown in Fig.
7.2.5a.
, and E are shown in Fig.
7.2.5a.

Piece-Wise Uniform Conductivity
With the resistor composed of uniformly
conducting layers in series, as shown in Fig. 7.2.5b, the potential
and conductance follow from (22) and (23) as
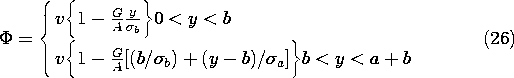

Again, there are no sources to distort the electric field in the
uniformly conducting regions. However, at the discontinuity in
conductivity, (17) shows that there is surface charge. For  b
>
b
>  a,
this surface charge is positive, tending to account for the more
intense field shown in Fig. 7.2.5b in the upper region.
a,
this surface charge is positive, tending to account for the more
intense field shown in Fig. 7.2.5b in the upper region.
Smoothly Varying Conductivity
With the exponential variation  =
=  o \exp (-y/d), (22)
and (23) become
o \exp (-y/d), (22)
and (23) become


Here the charge density that accounts for the distribution of E
follows from (16).

Thus, the field is shielded from the lower region by an exponentially
increasing volume charge density.
7.3 Distributed Current Sources and Associated Fields
Under steady conditions, conservation of charge requires that the
current density be solenoidal. Thus, J lines do not originate
or terminate. We have so far
thought of current tubes as originating outside the region of
interest, on the boundaries. It is sometimes convenient to introduce
a volume distribution of current sources, s(r, t) A/m3,
defined so that the steady charge conservation equation becomes
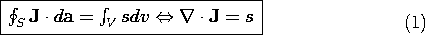
The motivation for introducing a distributed source of current
becomes clear as we now define singular sources and think about how
these can be realized physically.
Distributed Current Source Singularities
The analogy between (1) and
Gauss' law begs for the definition of point, line, and surface current
sources, as depicted in Fig. 7.3.1. In returning to Sec. 1.3 where
the analogous singular charge distributions were defined, it should be
kept in mind that we are now considering a source of current density,
not of electric flux.

A point source of current gives rise to a net current ip out of a
volume V that shrinks to zero while always enveloping the source.
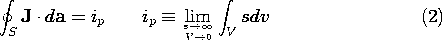
Such a source might be used to represent the current distribution
around a small electrode introduced into a conducting material. As
shown in Fig. 7.3.1d, the electrode is connected to a source of current
ip through an insulated wire. At least under steady conditions, the
wire and its insulation can be made fine enough so that the current
distribution in the surrounding conductor is not disturbed.
Note that if the wire and its insulation are considered, the
current density remains solenoidal. A surface surrounding the
spherical electrode is pierced by the wire. The contribution to the
integral of J  da from this part of the surface integral
is equal and
opposite to that of the remainder of the surface surrounding the
electrode. The point source is, in this case, an artifice for ignoring
the effect of the insulated wire on the current distribution.
da from this part of the surface integral
is equal and
opposite to that of the remainder of the surface surrounding the
electrode. The point source is, in this case, an artifice for ignoring
the effect of the insulated wire on the current distribution.
The tubular volume having a cross-sectional area A used to define
a line charge density in Sec. 1.3 (Fig. 1.3.4) is equally applicable
here to defining a line current density.

In general, Kl is a function of position
along the line, as shown in Fig. 7.3.1b. If this is the case, a
physical realization would require a bundle of insulated wires, each
terminated in an electrode segment delivering its current to the
surrounding medium, as shown in Fig. 7.3.1e. Most often, the line
source is used with two-dimensional flows and describes a uniform wire
electrode driven at one end by a current source.
The surface current source of Figs. 7.3.1c and 7.3.1f is defined using
the same incremental control volume enclosing the surface source as
shown in Fig. 1.3.5.

Note that Js is the net
current density entering the surrounding material at a given
location.
Fields Associated with Current Source Singularities
In the immediate vicinity of a point current source immersed in a
uniform conductor, the current distribution is spherically symmetric.
Thus, with J =  E, the integral current continuity law,
(1), requires that
E, the integral current continuity law,
(1), requires that

From this, the electric field intensity and potential of a point
source follow as
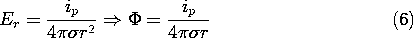
Example 7.3.1. Conductance of an Isolated Spherical Electrode
A simple way to measure the conductivity of a liquid is based on
using a small spherical electrode of radius a, as shown in Fig.
7.3.2. The electrode, connected to an insulated wire, is immersed in
the liquid of uniform conductivity  . The liquid is in a
container with a second electrode having a large area compared to that
of the sphere, and located many radii a from the sphere. Thus, the
potential drop associated with a current i that passes from the
spherical electrode to the large electrode is largely in the vicinity
of the sphere.
. The liquid is in a
container with a second electrode having a large area compared to that
of the sphere, and located many radii a from the sphere. Thus, the
potential drop associated with a current i that passes from the
spherical electrode to the large electrode is largely in the vicinity
of the sphere.

By definition the potential at the surface of the sphere is v, so
evaluation of the potential for a point source, (6), at r = a gives
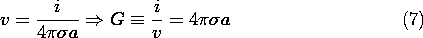
This conductance is analogous to the capacitance of an isolated
spherical electrode, as given by (4.6.8). Here, a fine insulated
wire connected to the sphere would have little effect on the current
distribution.
The conductance associated with a contact on a conducting material
is often approximated by picturing the contact as a
hemispherical electrode, as shown in Fig. 7.3.3. The region above the
surface is an insulator. Thus, there is no current density and hence
no electric field intensity normal to this surface. Note that this
condition is satisfied by the field associated with a point source
positioned on the conductor-insulator interface. An additional
requirement is that the potential on the surface of the electrode be
v. Because current is carried by only half of the spherical surface,
it follows from reevaluation of (6a) that the conductance of the
hemispherical surface contact is


The fields associated with uniform line and surface sources are
analogous to those discussed for line and surface charges in Sec. 1.3.
The superposition principle, as discussed for Poisson's equation
in Sec. 4.3, is equally applicable here. Thus, the fields associated
with higher-order source singularities can again be found by
superimposing those of the basic singular sources already defined.
Because it can be used to model a battery imbedded in a conductor, the
dipole source is of particular importance.
Example 7.3.2. Dipole Current Source in Spherical Coordinates
A positive point current source of magnitude ip is located at z =
d, just above a negative source (a sink) of equal magnitude at the
origin. The source-sink pair, shown in Fig. 7.3.4, gives rise to
fields analogous to those of Fig. 4.4.2. In the limit where the
spacing d goes to zero while the product of the source strength and
this spacing remains finite, this pair of sources forms a dipole.
Starting with the potential as given for a source at the origin by
(6), the limiting process is the same as leading to (4.4.8). The
charge dipole moment qd is replaced by the current dipole moment ip
d and  o
o 
 , qd \rightarrow ip d. Thus, the
potential of the dipole current source is
, qd \rightarrow ip d. Thus, the
potential of the dipole current source is


The potential of a polar dipole current source is found in Prob.
7.3.3.
Method of Images
With the new boundary conditions describing steady current
distributions come additional opportunities to exploit symmetry, as
discussed in Sec. 4.7. Figure 7.3.5 shows a pair of equal magnitude
point current sources located at equal distances to the right and
left of a planar surface. By contrast with the point charges of
Fig. 4.7.1, these sources are of the same sign. Thus, the
electric field normal to the surface is zero rather than the
tangential field. The field and current distribution in the right
half is the same as if that region were filled by a uniform conductor
and bounded by an insulator on its left.

7.4 Superposition and Uniqueness of Steady Conduction Solutions
The physical laws and boundary conditions are different, but the
approach in this section is similar to that
of Secs. 5.1 and 5.2 treating Poisson's equation.
In a material having the conductivity distribution  (r)
and source distribution s(r), a steady potential distribution
(r)
and source distribution s(r), a steady potential distribution
 must satisfy (7.2.4)
with a source density -s on the right. Typically,
the configurations of interest are as in Fig. 7.2.1, except that we
now include the possibility of a distribution of current source
density in the volume V. Electrodes are used to constrain this
potential over some of the surface enclosing the volume V occupied by
this material. This part of the surface, where the material contacts
the electrodes, will be called S'. We will assume here that on the
remainder of the enclosing surface, denoted by S", the normal current
density is specified. Depicted in Fig. 7.2.1 is the special case
where the boundary S" is insulating and hence where the normal
current density is zero. Thus, according to (7.2.1), (7.2.3), and
(7.3.1), the desired E and J are found from a solution
must satisfy (7.2.4)
with a source density -s on the right. Typically,
the configurations of interest are as in Fig. 7.2.1, except that we
now include the possibility of a distribution of current source
density in the volume V. Electrodes are used to constrain this
potential over some of the surface enclosing the volume V occupied by
this material. This part of the surface, where the material contacts
the electrodes, will be called S'. We will assume here that on the
remainder of the enclosing surface, denoted by S", the normal current
density is specified. Depicted in Fig. 7.2.1 is the special case
where the boundary S" is insulating and hence where the normal
current density is zero. Thus, according to (7.2.1), (7.2.3), and
(7.3.1), the desired E and J are found from a solution
 to
to

where

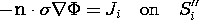
Except for the possibility that part of the boundary is a surface
S" where the normal current density rather than the potential
is specified, the situation here is analogous to that in Sec. 5.1.
The solution can be divided into a particular part [that satisfies the
differential equation of (1) at each point in the volume, but not
the boundary conditions] and a homogeneous part. The latter is then
adjusted to make the sum of the two satisfy the boundary conditions.
Superposition to Satisfy Boundary Conditions
Suppose that a system is
composed of a source-free conductor (s = 0) contacted by one reference
electrode at ground potential and n electrodes, respectively, at the
potentials vj, j = 1, \ldots n.
The contacting surfaces of these electrodes
comprise the surface S'. As shown in Fig. 7.2.1, there may be other
parts of the surface enclosing the material that are insulating (Ji
= 0) and denoted by S". The solution can be represented as
the sum of the
potential distributions associated with each of the electrodes
of specified potential while the others are grounded.

where
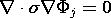
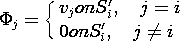
Each  j satisfies (1) with s = 0 and the boundary condition on
Si" with Ji = 0.
This decomposition of the solution is familiar from Sec. 5.1.
However, the boundary condition on the insulating surface S"
requires
a somewhat broadened view of what is meant by the respective terms in
(2). As the following example illustrates, modes that have zero
derivatives rather than zero amplitude at boundaries are now useful
for satisfying the insulating boundary condition.
j satisfies (1) with s = 0 and the boundary condition on
Si" with Ji = 0.
This decomposition of the solution is familiar from Sec. 5.1.
However, the boundary condition on the insulating surface S"
requires
a somewhat broadened view of what is meant by the respective terms in
(2). As the following example illustrates, modes that have zero
derivatives rather than zero amplitude at boundaries are now useful
for satisfying the insulating boundary condition.
Example 7.4.1. Modal Solution with an Insulating Boundary
In the two-dimensional configuration of Fig. 7.4.1, a uniformly
conducting material is grounded along its left edge, bounded by
insulating material along its right edge, and driven by electrodes
having the potentials v1 and v2 at the top and bottom,
respectively.

Decomposition of the potential, as called for by (2), amounts to
the superposition of the potentials for the two problems of (b) and
(c) in the figure. Note that for each of these, the normal derivative
of the potential must be zero at the right boundary.
Pictured in part (d) of Fig. 7.4.1 is a configuration familiar
from Sec. 5.5. The potential distribution for the configuration of
Fig. 5.5.2, (5.5.9), is equally applicable to that of Fig. 7.4.1.
This is so because the symmetry requires that there be no
x-directed electric field along the surface x = a/2. In turn,
the potential distribution for part (c) is readily determined from
this one by replacing v1  v2 and y \rightarrow b -
y. Thus, the total potential is
v2 and y \rightarrow b -
y. Thus, the total potential is
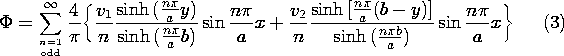
If we were to solve this problem without reference to Sec. 5.5,
the modes used to expand the electrode potential would be zero at x =
0 and have zero derivative at the insulating boundary (at x = a/2).
The Conductance Matrix
With Si' defined as the surface over which the i-th
electrode contacts the conducting material, the current emerging from
that electrode is

[See Fig. 7.2.1 for definition of direction of
da.] In terms of the potential decomposition represented by (2),
this expression becomes
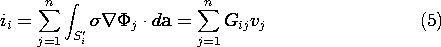
where the conductances are

Because  j is by definition proportional to vj, these
parameters are independent of the excitations. They depend only on the
physical properties and geometry of the configuration.
j is by definition proportional to vj, these
parameters are independent of the excitations. They depend only on the
physical properties and geometry of the configuration.
Example 7.4.2. Two Terminal Pair Conductance Matrix
For the system of Fig. 7.4.1, (5) becomes

With the potential given by (3), the self-conductances G11
and G22 and the mutual conductances G12 and G21
follow by evaluation of (5). This potential is singular in the
left-hand corners, so the self-conductances determined in this way
are represented by a series that does not converge. However, the
mutual conductances are determined by integrating the current density
over an electrode that is at the same potential as the grounded wall,
so they are well represented. For example, with c defined as the
length of the conducting block in the z direction,
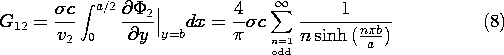
Uniqueness
With  i, Ji,
i, Ji,  (r), and s(r) given, a
steady current distribution is uniquely specified by the differential
equation and boundary conditions of (1).
As in Sec. 5.2, a proof that a second solution must be the same as
the first hinges on defining a difference potential
(r), and s(r) given, a
steady current distribution is uniquely specified by the differential
equation and boundary conditions of (1).
As in Sec. 5.2, a proof that a second solution must be the same as
the first hinges on defining a difference potential  d =
d =  a
-
a
-  b and showing that, because
b and showing that, because  d = 0 \quad on \quad
S'i and n
d = 0 \quad on \quad
S'i and n 

 d = 0 \quad on
\quad Si" in Fig. 7.2.1,
d = 0 \quad on
\quad Si" in Fig. 7.2.1,  d must be zero.
d must be zero.
7.5 Steady Currents in Piece-Wise Uniform Conductors
Conductor configurations are often made up from materials that are
uniformly conducting. The conductivity is then uniform in the
subregions occupied by the different materials but undergoes step
discontinuities at interfaces between regions. In the uniformly
conducting regions, the potential obeys Laplace's equation, (7.2.5),

while at the interfaces between regions, the continuity conditions
require that the normal current density and tangential electric field
intensity be continuous, (7.2.9) and (7.2.10).


Analogy to Fields in Linear Dielectrics
If the conductivity is
replaced by the permittivity, these laws are identical to those
underlying the examples of Sec. 6.6. The role played by D is now
taken by J. Thus, the analysis for the following example has already
been carried out in Sec. 6.6.
Example 7.5.1. Conducting Circular Rod in Uniform Transverse Field
A rod of radius R and conductivity  b is immersed in a
material of conductivity
b is immersed in a
material of conductivity  a,
as shown in Fig. 7.5.1. Perhaps
imposed by means of plane parallel electrodes far to the right and
left, there is a uniform current density far from the cylinder.
a,
as shown in Fig. 7.5.1. Perhaps
imposed by means of plane parallel electrodes far to the right and
left, there is a uniform current density far from the cylinder.

The potential distribution is deduced using the same steps as in
Example 6.6.2, with  a
a 
 a and
a and  b \rightarrow
b \rightarrow
 b. Thus, it follows from (6.6.21) and (6.6.22) as
b. Thus, it follows from (6.6.21) and (6.6.22) as
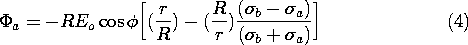
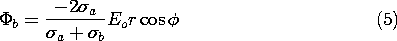
and the lines of electric field intensity are as shown in Fig.
6.6.6. Note that although the lines of E and J are in
the same direction and have the same pattern in each of the regions,
they have very different behaviors where the conductivity is
discontinuous. In fact, the normal component of the current density
is continuous at the interface, and the spacing between lines of
J must be preserved across the interface. Thus, in the
distribution of current density shown in Fig. 7.5.2, the lines are
continuous. Note that the current tends to concentrate on the rod if
it is more conducting, but is diverted around the rod if it is more
insulating.

A surface charge density resides at the interface between the
conducting media of different conductivities. This surface charge
density acts as the source of E on the cylindrical surface and
is identified by (7.2.17).
Inside-Outside Approximations
In exploiting the formal analogy between
fields in linear dielectrics and in Ohmic conductors, it is important
to keep in mind the very different physical phenomena being described.
For example, there is no conduction analog to the free space
permittivity  o. There is no minimum value of the
conductivity, and although
o. There is no minimum value of the
conductivity, and although  can vary between a minimum of
can vary between a minimum of  o
in free space and 1000
o
in free space and 1000  o or more in special solids, the electrical
conductivity is even more widely varying. The ratio of the
conductivity of a copper wire to
that of its insulation exceeds 1021.
o or more in special solids, the electrical
conductivity is even more widely varying. The ratio of the
conductivity of a copper wire to
that of its insulation exceeds 1021.
Because some materials are very good conductors while others
are very good insulators, steady conduction problems can exemplify the
determination of fields for large ratios of physical parameters. In Sec.
6.6, we examined field distributions in cases
where the ratios of permittivities were very large or very
small. The "inside-outside" viewpoint is applicable not only
to approximating fields in dielectrics but to finding the
fields in the transient EQS systems in the latter part
of this chapter and in MQS systems with magnetization and conduction.
Before attempting a more general approach, consider the
following example, where the fields in and around a resistor are
described.
Example 7.5.2. Fields in and around a Conductor
The circular cylindrical conductor of Fig. 7.5.3, having radius b
and length L, is surrounded by a perfectly conducting circular
cylindrical "can" having inside radius a. With respect to the
surrounding perfectly conducting shield, a dc voltage source applies a
voltage v to the perfectly conducting disk. A washer-shaped material
of thickness  and also having conductivity
and also having conductivity  is
connected between the perfectly conducting disk and the outer can.
What are the distributions of
is
connected between the perfectly conducting disk and the outer can.
What are the distributions of  and E in the conductors
and in the annular free space region?
and E in the conductors
and in the annular free space region?

Note that the fields within each of the conductors are fully
specified without regard for the shape of the can. The surfaces of
the circular cylindrical conductor are
either constrained in potential or bounded by free space. On the
latter, the normal component of J, and hence of E, is
zero. Thus, in the language of Sec. 7.4, the potential is
constrained on S' while the
normal derivative of  is constrained on the insulating surfaces
S". For the center conductor, S' is at z = 0 and z =
-L while S" is at r = b. For the washer-shaped conductor,
S' is at r = b and r = a and S" is at z = -L and z
= -(L +
is constrained on the insulating surfaces
S". For the center conductor, S' is at z = 0 and z =
-L while S" is at r = b. For the washer-shaped conductor,
S' is at r = b and r = a and S" is at z = -L and z
= -(L +  ). The theorem of Sec. 7.4 shows that the potential
inside each of the conductors is uniquely specified. Note that
this is true regardless of the arrangement outside the
conductors.
). The theorem of Sec. 7.4 shows that the potential
inside each of the conductors is uniquely specified. Note that
this is true regardless of the arrangement outside the
conductors.
In the cylindrical conductor, the solution for the potential that
satisfies Laplace's equation and all these boundary conditions is
simply a linear function of z.

Thus, the electric field intensity is uniform and z directed.

These equipotentials and E lines are sketched in Fig. 7.5.4. By way
of reinforcing what is new about the insulating surface boundary
condition, note that (6) and (7) apply to the cylindrical conductor
regardless of its cross-section geometry and its length.
However, the longer it is, the more stringent is the requirement that
the annular region be insulating compared to the central region.

In the washer-shaped conductor, the axial symmetry requires that
the potential not depend on z. If it depends only on the radius, the
boundary conditions on the insulating surfaces are automatically
satsfied. Two solutions to Laplace's equation are required to meet
the potential constraints at r = a and r = b. Thus, the solution is
assumed to be of the form

The coefficients A and B are determined from the radial boundary
conditions, and it follows that the potential within the washer-shaped
conductor is

The "inside" fields can now be used to determine those in the
insulating annular "outside" region. The potential is determined on
all of the surface surrounding this region. In addition to being zero
on the surfaces r = a and z = 0, the potential is given by (6) at
r = b and by (9) at
z = -L. So, in turn, the potential in this annular region is
uniquely determined.
This is one of the few problems in this book where solutions to
Laplace's equation that have both an r and a z dependence are
considered. Because there is no  dependence, Laplace's equation
requires that
dependence, Laplace's equation
requires that
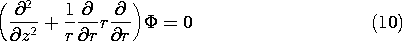
The linear dependence on z of the potential at r = b suggests that
solutions to Laplace's equation take the product form R(r)z.
Substitution into (10) then shows that the r dependence is the same
as given by (9). With the coefficients adjusted to make the
potential  a(a, -L) = 0 and
a(a, -L) = 0 and  a(b, -L) = v, it follows that
in the outside insulating region
a(b, -L) = v, it follows that
in the outside insulating region

To sketch this potential and the associated E lines in Fig.
7.5.4, observe that the equipotentials join points of the given
potential on the central conductor with those of the same potential on
the washer-shaped conductor. Of course, the zero potential surface is
at r = a and at z = 0. The lines of electric field intensity that
originate on the surfaces of the conductors are perpendicular
to these equipotentials and have tangential components that
match those of the inside fields. Thus, at the surfaces of the finite
conductors, the electric field in region (a) is neither perpendicular
nor tangential to the boundary.
For a positive potential v, it is clear that there must be
positive surface charge on the surfaces of the conductors bounding the
annular insulating region. Remember that the normal component of E on
the conductor sides of these surfaces is zero. Thus, there is a surface
charge that is proportional to the normal component of E on the
insulating side of the surfaces.
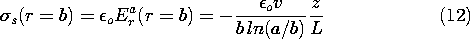
The order in which we have determined the fields makes it clear that
this surface charge is the one required to accommodate the field
configuration outside the conducting regions. A change in the shield
geometry changes  a but does not alter the current
distribution within the conductors. In terms of the circuit analogy
used in Sec. 7.0, the potential distributions have been completely
determined by the rod-shaped and washer-shaped resistors. The charge
distribution is then determined ex post facto by the "distributed
capacitors" surrounding the resistors.
a but does not alter the current
distribution within the conductors. In terms of the circuit analogy
used in Sec. 7.0, the potential distributions have been completely
determined by the rod-shaped and washer-shaped resistors. The charge
distribution is then determined ex post facto by the "distributed
capacitors" surrounding the resistors.
The following demonstration shows that the unpaired
charge density is zero in the volume of a uniformly conducting
material and that charges do indeed tend to accumulate at
discontinuities of conductivity.
Demonstration 7.5.1. Distribution of Unpaired Charge
A box is constructed so that two of its sides and its bottom are
plexiglas, the top is open, and the sides shown to left and right in
Fig. 7.5.5 are highly conducting. It is filled with corn oil so that
the region between the vertical electrodes in Fig. 7.5.5 is
semi-insulating. The region above the free surface is air and
insulating compared to the corn oil. Thus, the corn oil plays a role
analogous to that of the cylindrical rod in Example 7.5.2.
Consistent with its insulating transverse boundaries and the
potential constraints to left and right is an "inside" electric
field that is uniform.

The electric field in the outside region (a) determines the
distribution of charge on the interface. Since we have determined
that the inside field is uniform, the potential of the interface varies
linearly from v at the right electrode to zero at the left electrode.
Thus, the equipotentials are evenly spaced along the interface. The
equipotentials in the outside region (a) are planes joining the inside
equipotentials and extending to infinity, parallel to the canted
electrodes. Note that this field satisfies the boundary conditions on
the slanted electrodes and matches the potential on the liquid
interface. The electric field intensity is uniform,
originating on the upper electrode and terminating either on the
interface or on the lower slanted electrode. Because both the spacing
and the potential difference vary linearly with horizontal distance,
the negative surface charge induced on the interface is uniform.
Wherever there is an unpaired charge density, the corn oil is
subject to an electrical force. There is
unpaired charge in the immediate vicinity of the interface in the
form of a surface charge, but not in
the volume of the conductor. Consistent with this prediction is the
observation that with the application of about 20 kV to electrodes
having 20 cm spacing, the liquid is set into a circulating motion. The
liquid moves rapidly to the right at the interface and recirculates in
the region below. Note that the force at the interface is indeed to
the right because it is proportional to the product of a negative
charge and a negative electric field intensity. The fluid moves as
though each part of the interface is being pulled to the right. But
how can we be sure that the circulation is not due to forces on
unpaired charges in the fluid volume?
An alteration to the same experiment answers this question. With
a plexiglas sheet placed on the interface, it is mechanically pinned
down. That is, the electrical force acting on the unpaired charges in
the immediate vicinity of the interface is countered by viscous
forces tending to prevent the fluid from moving tangential to the
solid boundary. Yet because the sheet is insulating, the field
distribution within the conductor is presumably unaltered from what it
was before.
With the plexiglas sheet in place, the circulations of the first
experiment are no longer observed. This is consistent with a model
that represents the corn-oil as a uniform Ohmic
conductor
1 See film Electric Fields and
Moving Media, produced by the National Committee for Electrical
Engineering Films and distributed by Education Development Center, 39
Chapel St., Newton, Mass. 02160.. (For a mathematical analysis, see
Prob. 7.5.3.)
In general, there is a two-way coupling between the fields in
adjacent uniformly conducting regions. If the ratio of conductivities
is either very large or very small, it is possible to calculate the
fields in an "inside" region ignoring the effect of "outside"
regions, and then to find the fields in the "outside" region.
The region in which the field is first found, the "inside"
region, is usually the one to which the excitation is applied, as
illustrated in Example 7.5.2. This will be further illustrated in
the following example, which pursues an approximate treatment of Example
7.5.1. The exact solutions found there can then be compared to the
approximate ones.
Example 7.5.3. Approximate Current Distribution around Relatively
Insulating and Conducting Rods
Consider first the field distribution around and then in a
circular rod that has a small conductivity relative to its
surroundings. Thus, in Fig. 7.5.1,  a \gg
a \gg  b.
Electrodes far to the left and right are used to apply a uniform field
and current density to region (a). It is therefore in this inside
region outside the cylinder that the fields are first approximated.
b.
Electrodes far to the left and right are used to apply a uniform field
and current density to region (a). It is therefore in this inside
region outside the cylinder that the fields are first approximated.
With the rod relatively insulating, it imposes on region (a) the
approximate boundary condition that the normal current density, and
hence the radial derivative of the potential, be zero at the rod
surface, where r = R.
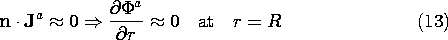
Given that the field at infinity must be uniform, the potential
distribution in region (a) is now uniquely specified. A solution to
Laplace's equation that satisfies this condition at infinity and includes
an arbitrary coefficient for hopefully satisfying the first condition
is
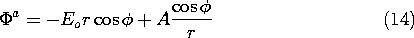
With A adjusted to satisfy (13), the approximate potential in region
(a) is
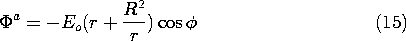
This is the potential in the exterior region,
implying the field lines shown in Fig. 7.5.6a.

Now that we have obtained the approximate potential at r = R,
 b = - 2Eo R cos (
b = - 2Eo R cos ( ), we can in turn approximate the
potential in region (b).
), we can in turn approximate the
potential in region (b).
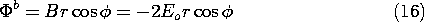
The field lines associated with this potential are also shown
in Fig. 7.5.6a. Note that if we take the limits of (4) and (5)
where  a /
a / b \gg 1, we obtain these potentials.
b \gg 1, we obtain these potentials.
Contrast these steps with those that are appropriate in the
opposite extreme, where  a /
a / b \ll 1.
There the rod tends to behave as an
equipotential and the boundary condition at r = R is
b \ll 1.
There the rod tends to behave as an
equipotential and the boundary condition at r = R is  a =
constant = 0. This condition is now used to evaluate the
coefficient A in (14) to obtain
a =
constant = 0. This condition is now used to evaluate the
coefficient A in (14) to obtain
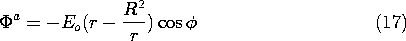
This potential implies that there is a current density at the rod
surface given by
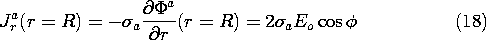
The normal current density at the inside surface of the rod must be
the same, so the coefficient B in (16) can be evaluated.

Now the field lines are as shown in Fig. 7.5.6b.
Again, the approximate potential distributions given by (17)
and (19), respectively, are consistent with what is obtained from the
exact solutions, (4) and (5), in the limit  a /
a / b \ll
1.
b \ll
1.
In the following demonstration, a surprising electromechanical
response has its origins in the charge distribution implied by the
potential distributions found in Example 7.5.3.
Demonstration 7.5.2. Rotation of an Insulating Rod in a Steady Current
In the apparatus shown in Fig. 7.5.7, a teflon rod is mounted at
its ends on bearings so that it is free to rotate. It, and a pair of
plane parallel electrodes, are immersed in corn oil.
Thus, from the top, the configuration is as shown in Fig. 7.5.1. The
applied field Eo = v/d, where v is the voltage applied between the
electrodes and d is their spacing. In the experiment, R = 1.27 cm ,
d = 11.8 cm, and the applied voltage is 10-20 kV.

As the voltage is raised, there is a threshold at which the rod
begins to rotate. With the voltage held fixed at a level above the
threshold, the ensuing rotation is continuous and in either
direction. [See footnote 1.]
To explain this "motor," note that even though the corn oil used
in the experiment has a conductivity of  a = 5 x 10-11
S/m, that is still much greater than the conductivity
a = 5 x 10-11
S/m, that is still much greater than the conductivity  b of
the rod. Thus, the potential around and in the rod is given by (15)
and (16) and the E field distribution is as shown in Fig.
7.5.6a. Also shown in this figure is the distribution of unpaired
surface charge, which can be evaluated using (16).
b of
the rod. Thus, the potential around and in the rod is given by (15)
and (16) and the E field distribution is as shown in Fig.
7.5.6a. Also shown in this figure is the distribution of unpaired
surface charge, which can be evaluated using (16).
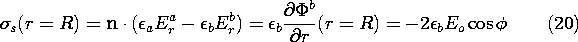
Positive charges on the left electrode induce charges of the
same sign
on the nearer side of the rod, as do the negative charges on the
electrode to the right. Thus, when static, the rod is in a posture
analogous to that of a compass needle oriented backwards in a magnetic
field. Its static state is unstable and it attempts to reorient
itself in the field. The continuous rotation results because once it
begins to rotate, additional fields are generated that allow the
charge to leak off the cylinder through currents in the surrounding
oil.
Note that if the rod were much more conducting than its
surroundings, charges on the electrodes would induce charges of
opposite sign on the nearer surfaces of the rod. This more familiar
situation is the one shown in Fig. 7.5.6b.
The condition requiring that there be no normal current density
at an insulating boundary can have a dramatic effect on fringing
fields. This has already been illustrated by Example 7.5.2, where the
field was uniform in the central conductor no matter what its length
relative to its radius. Whenever we take the resistance of a wire
having length L, cross-sectional area A, and conductivity
 as being L/
as being L/ A, we exploit this boundary condition.
A, we exploit this boundary condition.
The conduction analogue of Example 6.6.3 gives a further
illustration of how an insulating boundary ducts the electric field
intensity. With  a
a 
 a and
a and  b \rightarrow
b \rightarrow
 b, the configuration of Fig. 6.6.8 becomes
the edge of a plane parallel resistor filled out to the edge of the
electrodes by a material having conductivity
b, the configuration of Fig. 6.6.8 becomes
the edge of a plane parallel resistor filled out to the edge of the
electrodes by a material having conductivity  b. The fringing field
then depends on the conductivity
b. The fringing field
then depends on the conductivity  a of the surrounding material.
a of the surrounding material.
The fringing field that would result if the entire region were
filled by a material having a uniform conductivity is shown in Fig.
6.6.9a. By contrast, the field distribution with the conducting
material extending only to the edge of the electrode is shown in Fig.
6.6.9b. The field inside is exactly uniform and independent of the
geometry of what is outside. Of course, there is always a fringing
field outside that does depend on the outside geometry. But because
there is little associated current density, the resistance is
unaffected by this part of the field.
7.6 Conduction Analogs
The potential
distribution for steady conduction is determined by solving (7.4.1)

in a volume V having conductivity  (r) and current
source distribution s(r), respectively.
(r) and current
source distribution s(r), respectively.
On the other hand, if the volume is filled by a perfect dielectric
having permittivity  (r) and unpaired charge density
distribution
(r) and unpaired charge density
distribution  u (r), respectively, the
potential distribution is determined by the combination of (6.5.1)
and (6.5.2).
u (r), respectively, the
potential distribution is determined by the combination of (6.5.1)
and (6.5.2).

It is clear that solutions pertaining to one of these physical situations
are solutions for the other, provided that the boundary conditions
are also analogous. We have been exploiting
this analogy in Sec. 7.5 for piece-wise continuous systems. There,
solutions for the fields in dielectrics were applied to conduction
problems. Of course, measurements made on dielectrics can also be
used to predict steady conduction phemonena.
Conversely, fields found either theoretically or by
experimentation in a steady conduction situation can be used to
describe those in perfect dielectrics. When measurements are used, the
latter procedure is a particularly useful one, because conduction
processes are conveniently simulated and comparatively easy to measure.
It is more difficult to measure the potential in free space than
in a conductor, and to measure a capacitance than a resistance.
Formally, a quantitative analogy is established by introducing the
constant ratios for the magnitudes of the properties, sources, and
potentials, respectively, in the two systems
throughout the volumes and on the boundaries. With k1 and k2
defined as scaling constants,
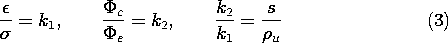
substitution of the conduction variables into (2) converts it into
(1). The boundary conditions on surfaces S' where the potential is
constrained are analogous, provided the boundary potentials also have
the constant ratio k2 given by (3).
Most often, interest is in systems where there are no volume
source distributions. Thus, suppose that the capacitance of a pair of
electrodes is to be determined by measuring the conductance of
analogously shaped electrodes immersed in a conducting material. The
ratio of the measured capacitance to conductance, the ratio of
(6.5.6) to (7.2.15), follows from substituting  = k1
= k1 , (3a),
, (3a),
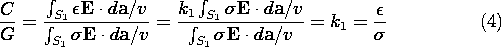
In multiple terminal pair systems, the capacitance matrix defined by
(5.1.12) and (5.1.13) is similarly deduced from measurement of a
conductance matrix, defined in (7.4.6).
Demonstration 7.6.1. Electrolyte-Tank Measurements
If great accuracy is required, fields in complex geometries are
most easily determined numerically. However, especially if the
capacitance is sought- and not a detailed field mapping-
a conduction analog can prove convenient. A simple experiment to
determine the capacitance of a pair of electrodes is shown in Fig.
7.6.1, where they are mounted on insulated rods, contacted through
insulated wires, and immersed in tap water. To avoid electrolysis,
where the conductors contact the water, low-frequency ac is used.
Care should be taken to insure that boundary conditions imposed by the
tank wall are either analogous or inconsequential.

Often, to motivate or justify approximations used in analytical
modeling of complex systems, it is helpful to probe the potential
distribution using such an experiment. The probe consists of a small
metal tip, mounted and wired like the electrodes, but connected to a
divider. By setting the probe potential to the desired rms value, it
is possible to trace out equipotential surfaces by moving the probe in
such a way as to keep the probe current nulled. Commercial equipment
is automated with a feedback system to perform such measurements with
great precision. However, given the alternative of numerical
simulation, it is more likely that such approaches are appropriate in
establishing rough approximations.
Mapping Fields that Satisfy Laplace's Equation
Laplace's equation determines the potential distribution in a volume
filled with a material of uniform conductivity that is source free.
Especially for two-dimensional fields, the conduction analog then
also gives the opportunity to refine the art of sketching the
equipotentials of solutions to Laplace's equation and the associated
field lines.
Before considering how a sheet of conducting paper provides the
medium for determining two-dimensional fields, it is worthwhile to
identify the properties of a field sketch that indeed represents a
two-dimensional solution to Laplace's equation.
A review of the many two-dimensional plots of equipotentials and
fields given in Chaps. 4 and 5 shows that they form a grid of
curvilinear rectangles.
In terms of variables defined for the field sketch of
Fig. 7.6.2, where the distance between equipotentials is denoted by
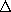 n and the distance between E lines is
n and the distance between E lines is 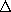 s, the ratio
s, the ratio
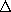 n/
n/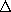 s tends to be constant, as we shall now show.
s tends to be constant, as we shall now show.

The condition that the field be irrotational gives
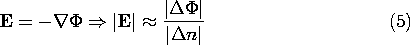
while the steady charge conservation law implies that along a flux
tube,

Thus, along a flux tube,
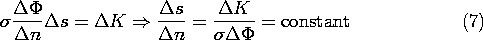
If each of the flux tubes carries the same current, and if the
equipotential lines are drawn for equal increments of 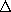
 , then
the ratio
, then
the ratio 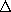 s/
s/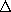 n must be constant throughout the mapping.
The sides of the curvilinear rectangles are commonly made equal,
so that the
equipotentials and field lines form a grid of curvilinear squares.
n must be constant throughout the mapping.
The sides of the curvilinear rectangles are commonly made equal,
so that the
equipotentials and field lines form a grid of curvilinear squares.
The faithfulness to Laplace's equation of a map of equipotentials
at equal increments in potential can be checked by sketching in the
perpendicular field lines. With the field lines forming curvilinear
squares in the starting region, a correct distribution of the
equipotentials is achieved when a grid of squares is maintained
throughout the region.
With some practice, it is possible to iterate between refinements of
the equipotentials and the field lines until a satisfactory map of the
solution is sketched.
\begindemo2Two-Dimensional Solution to Laplace's
Equation by Means of Teledeltos Paper
For the mapping of two-dimensional fields, the conduction
analog has the advantage that it is not necessary to make the
electrodes and conductor "infinitely" long in the third dimension.
Two-dimensional current distributions will result even in a thin-sheet
conductor, provided that it has a conductivity that is large compared
to its surroundings. Here again we exploit the boundary condition
applying to the surfaces of the paper. As far as the fields inside
the paper are concerned, a two-dimensional current distribution
automatically meets the requirement that there be no current density
normal to those parts of the paper bounded by air.
A typical field mapping apparatus is as simple as that shown in
Fig. 7.6.3. The paper has the thickness 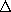 and a conductivity
and a conductivity
 .
The electrodes take the form of silver paint or copper tape put on
the upper surface of the paper, with a shape simulating the electrodes
of the actual system. Because the paper is so thin compared to
dimensions of interest in the plane of the paper surface, the currents
from the electrodes quickly assume an essentially uniform profile over
the cross-section of the paper, much as suggested by the inset to Fig.
7.6.3.
.
The electrodes take the form of silver paint or copper tape put on
the upper surface of the paper, with a shape simulating the electrodes
of the actual system. Because the paper is so thin compared to
dimensions of interest in the plane of the paper surface, the currents
from the electrodes quickly assume an essentially uniform profile over
the cross-section of the paper, much as suggested by the inset to Fig.
7.6.3.

In using the paper, it is usual to deal in terms of a surface
resistance 1/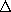
 . The conductance of the plane parallel
electrode system shown in Fig. 7.6.4 can be used to establish this
parameter.
. The conductance of the plane parallel
electrode system shown in Fig. 7.6.4 can be used to establish this
parameter.
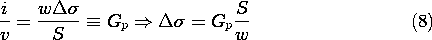

The units are simply ohms, and 1/
 is the resistance of a
square of the material having any sidelength. Thus, the units are
commonly denoted as "ohms/square."
is the resistance of a
square of the material having any sidelength. Thus, the units are
commonly denoted as "ohms/square."
To associate a conductance as measured at the terminals of the
experiment shown in Fig. 7.6.3 with the capacitance of a pair of
electrodes having length l in the third dimension, note that the
surface integrations used to define C and G reduce to
where the surface integrals have been reduced to line integrals by
carrying out the integration in the third dimension. The ratio of
these quantities follows in terms of the surface conductance
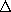
 as
as

Here G is the conductance as actually measured using the conducting
paper, and C is the capacitance of the two-dimensional capacitor it
simulates.
In Chap. 9, we will find that magnetic field distributions as well
can often be found by using the conduction analog.
7.7 Charge Relaxation in Uniform Conductors
In a region that has uniform conductivity and permittivity,
charge conservation and Gauss' law determine the unpaired charge
density throughout the volume of the material, without regard
for the boundary conditions. To see this, Ohm's law (7.1.7) is
substituted for the current density in the charge conservation law,
(7.0.3),

and Gauss' law (6.2.15) is written using the linear polarization
constitutive law, (6.4.3).

In a region where  and
and  are uniform, these parameters can
be pulled
outside the divergence operators in these equations. Substitution of
div E found from (2) into (1) then gives the charge relaxation
equation for
are uniform, these parameters can
be pulled
outside the divergence operators in these equations. Substitution of
div E found from (2) into (1) then gives the charge relaxation
equation for  u.
u.

Note that it has not been assumed that E is irrotational, so the
unpaired charge obeys this equation whether the fields are EQS or not.
The solution to (3) takes on the same appearance as if it were
an ordinary differential equation, say predicting the voltage of an RC
circuit.

However, (3) is a partial differential equation, and so the
coefficient of the exponential in (4) is an arbitrary function of
the spatial coordinates. The relaxation time  e
has the typical values illustrated in Table 7.7.1.
e
has the typical values illustrated in Table 7.7.1.

The function  i (x, y, z) is the unpaired charge density when t
= 0. Given any initial distribution, the subsequent distribution of
i (x, y, z) is the unpaired charge density when t
= 0. Given any initial distribution, the subsequent distribution of
 u is given by (4).
Once the unpaired charge density has decayed to zero
at a given point, it will remain zero. This is true regardless of
the constraints on the surface bounding the region of uniform
u is given by (4).
Once the unpaired charge density has decayed to zero
at a given point, it will remain zero. This is true regardless of
the constraints on the surface bounding the region of uniform  and
and  . Except for a transient that can only be initiated from
very special initial conditions, the unpaired charge density in a
material of uniform conductivity and permittivity is zero. This is
true even if the system is not EQS.
. Except for a transient that can only be initiated from
very special initial conditions, the unpaired charge density in a
material of uniform conductivity and permittivity is zero. This is
true even if the system is not EQS.
The following example is intended to help emphasize these
implications of (3) and (4).
Example 7.7.1. Charge Relaxation in Region of Uniform  and
and

In the region of uniform  and
and  shown in Fig. 7.7.1, the
initial distribution of unpaired charge density is
shown in Fig. 7.7.1, the
initial distribution of unpaired charge density is

where  o is a constant.
o is a constant.
It follows from (4) that the subsequent distribution is
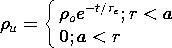
As pictured in Fig. 7.7.1, the charge density in the spherical region
r < a remains uniform as it decays to zero with the time constant
 e. The charge density in the surrounding region is initially
zero and remains so throughout the transient.
e. The charge density in the surrounding region is initially
zero and remains so throughout the transient.
Charge conservation implies that there must be a current density
in the material surrounding the initially charged spherical region.
Yet, according to the laws used here, there is never a net unpaired
charge density in that region. This is possible because in Ohmic
conduction, there are at least two types of charges involved. In the
uniformly conducting material, one or both of these migrate in the
electric field caused by the net charge [in accordance with (7.1.5)]
while exactly neutralizing each other so that  u = 0 (7.1.6).
u = 0 (7.1.6).
\sectnonumNet Charge on Bodies Immersed in Uniform
Materials
2 This subsection is not essential to the
material that follows.
The integral charge relaxation law, (1.5.2), applies to the net
charge within any volume containing a medium of constant  and
and
 . If an initially charged particle finds itself
suspended in a fluid having uniform
. If an initially charged particle finds itself
suspended in a fluid having uniform  and
and  , this charge
must decay with the charge relaxation time constant
, this charge
must decay with the charge relaxation time constant  e.
e.

Demonstration 7.7.1. Relaxation of Charge on Particle in Ohmic Conductor
The pair of plane parallel electrodes shown in Fig. 7.7.2 is
immersed in a semi-insulating liquid, such as corn oil, having a
relaxation time on the order of a second. Initially, a metal particle
rests on the lower electrode. Because this particle makes electrical
contact with the lower electrode, application of a potential
difference results in charge being induced not only on the surfaces of
the electrodes but on the surface of the particle as well. At the
outset, the particle is an extension of the lower electrode. Thus,
there is an electrical force on the particle that is upward. Note
that changing the polarity of the voltage changes the sign of both the
particle charge and the field, so the force is always upward.

As the voltage is raised, the electrical force outweighs the net
gravitational force on the particle and it lifts off. As it separates
from the lower electrode, it does so with a net charge sufficient to
cause the electrical force to start it on its way toward charges of the
opposite sign on the upper electrode. However, if the liquid is an
Ohmic conductor with a relaxation time shorter than that
required for the particle to reach the upper electrode, the net charge on the
particle decays, and the upward electrical force falls
below that of the downward gravitational force. In this case,
the particle falls back to the lower electrode without reaching the
upper one. Upon contacting the lower electrode, its charge is renewed
and so it again lifts off. Thus, the particle appears to bounce on
the lower electrode.
By contrast, if the oil has a relaxation time long enough so
that the particle can reach the upper electrode before a significant
fraction of its charge is lost, then the particle makes rapid
excursions between the electrodes. Contact with the upper electrode
results in a charge reversal and hence a reversal in the electrical
force as well.
The experiment demonstrates that as long as a particle is
electrically isolated in an Ohmic conductor, its charge will decay to
zero and will do so with a time constant that is the relaxation time
 /
/ . According to the Ohmic model, once the particle is
surrounded by a uniformly conducting material, it cannot be
given a net charge by any manipulation of the potentials on electrodes
bounding the Ohmic conductor. The charge can only change upon
contact with one of the electrodes.
. According to the Ohmic model, once the particle is
surrounded by a uniformly conducting material, it cannot be
given a net charge by any manipulation of the potentials on electrodes
bounding the Ohmic conductor. The charge can only change upon
contact with one of the electrodes.
We have found that a particle immersed in an Ohmic conductor can
only discharge. This is true even if it finds itself in a region
where there is an externally imposed conduction current. By contrast,
the next example illustrates how a unipolar conduction process
can be used to charge a particle. The ion-impact charging (or field
charging) process is put to work in electrophotography and
air pollution control.
Example 7.7.2. Ion-Impact Charging of Macroscopic Particles
The particle shown in Fig. 7.7.3 is itself perfectly conducting.
In its absence, the surrounding region is filled by an un-ionized gas
such as air permeated by a uniform z-directed electric field.
Positive ions introduced at z  -
- then give rise
to a unipolar
current having a density given by the unipolar conduction law,
(7.1.8). With the introduction of the particle, some of the lines of
electric field intensity can terminate on the particle. These carry
ions to the particle. Other lines originate on the particle and it is
assumed that there is no mechanism for the particle surface to
initiate ions that would then carry charge away from the particle
along these lines. Thus, as the particle intercepts some of the ion
current, it charges up.
then give rise
to a unipolar
current having a density given by the unipolar conduction law,
(7.1.8). With the introduction of the particle, some of the lines of
electric field intensity can terminate on the particle. These carry
ions to the particle. Other lines originate on the particle and it is
assumed that there is no mechanism for the particle surface to
initiate ions that would then carry charge away from the particle
along these lines. Thus, as the particle intercepts some of the ion
current, it charges up.

Here the particle-charging process is described as a sequence of
steady states. The charge conservation equation (7.0.3) obtained
by using the unipolar conduction law (7.1.8) then requires that

Thus, the "field"  E (consisting of the product of the
charge density and the electric field intensity)
forms flux tubes. These have walls tangential to E and
incremental cross-sectional areas
E (consisting of the product of the
charge density and the electric field intensity)
forms flux tubes. These have walls tangential to E and
incremental cross-sectional areas  a, as illustrated in
Figs.7.7.3 and 2.7.5, such that
a, as illustrated in
Figs.7.7.3 and 2.7.5, such that  E
E 
 a remains
constant.
a remains
constant.
As a second approximation, it is assumed that the dominant sources
for the electric field are on the boundaries, either on the surface of
the particle or at infinity. Thus, the ions in the
volume of the gas are low enough in concentration so that their volume
charge density makes a negligible contribution to
the electric field intensity. At each point in the volume of the gas,

From this statement of Gauss' law, it follows that the E
lines also form flux tubes along which E 
 a
is conserved. Because
both E
a
is conserved. Because
both E 
 a and
a and  E \cdot
E \cdot  a are
constant along
a given E line, it is necessary that the charge density
a are
constant along
a given E line, it is necessary that the charge density  be
constant along these lines. This fact will now be used to calculate
the current of ions to the particle.
be
constant along these lines. This fact will now be used to calculate
the current of ions to the particle.
At a given instant in the charging process, the particle has a
net charge q. Its surface is an equipotential and it finds itself in
an electric field that is uniform at infinity. The distribution of
electric field for this situation was found in Example 5.9.2. Lines of
electric field intensity terminate on the southern end of the sphere
over the range  \geq
\geq  \geq
\geq  c, where
c, where 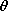 c is
shown in Figs. 7.7.3 and 5.9.2. In view of the unipolar conduction
law, these lines carry with them a current density. Thus, there is a
net current into the particle given by
c is
shown in Figs. 7.7.3 and 5.9.2. In view of the unipolar conduction
law, these lines carry with them a current density. Thus, there is a
net current into the particle given by
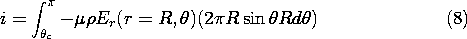
Because  is constant along an electric field line and
is constant along an electric field line and  is
uniform far from the charge-collecting particles, it is a constant
over the surface of integration.
is
uniform far from the charge-collecting particles, it is a constant
over the surface of integration.
It follows from (5.9.13) that the normal electric field needed to
evaluate (8) is
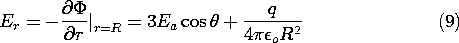
Substitution of (9) into (8) gives
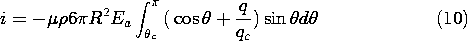
where, as in Example 5.9.2, qc = 12 
 o R2 Ea and
o R2 Ea and

Remember, 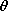 c is the angle at which the radial electric field
switches from being outward to inward. Thus, it is a function of the
amount of charge on the particle. Substitution of (11) into (10) and
some manipulation gives the net current to the particle as
c is the angle at which the radial electric field
switches from being outward to inward. Thus, it is a function of the
amount of charge on the particle. Substitution of (11) into (10) and
some manipulation gives the net current to the particle as

where  i = 4
i = 4 o /
o /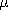
 .
.
From (10) it is clear that the current depends on the particle
charge. As charge accumulates on the particle, the angle 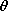 c
increases and so the southern surface over which electric field lines
terminate decreases. By the time q = qc, the collection
surface is zero and, as implied by (12), the current goes to zero.
c
increases and so the southern surface over which electric field lines
terminate decreases. By the time q = qc, the collection
surface is zero and, as implied by (12), the current goes to zero.
If the charging process is slow enough to be viewed as a sequence
of stationary states, the current given by (12) is equal to the rate
of increase of the particle charge.
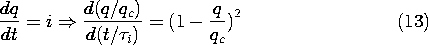
Divided by what is on the right and multiplied by the denominator on
the left, this expression can be integrated.
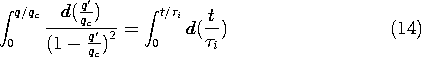
The result is a charging law that is not exponential but rather


This charging transient is shown in Fig. 7.7.4. By contrast with a
particle placed in a conduction current that is Ohmic, a particle
subjected to a unipolar current will charge up to the saturation
charge qc. Note that the charging time,  i = 4
i = 4 o
/
o
/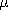
 , again takes the form of
, again takes the form of  divided by a "conductivity."
divided by a "conductivity."
Demonstration 7.7.2. Electrostatic Precipitation
Once dust, smoke, or fume particles are charged, they can be
subjected to an electric field and pulled out of the gas in which they
are interspersed. In large precipitators used to filter combustion gases
before they are released from a stack, the charging and precipitation
processes are carried out in one region. The apparatus of Fig. 7.7.5
illustrates this process.

A fine wire is stretched along the axis of a grounded conducting
cylinder having a radius of 5-10 cm. With the wire at a voltage of
10-30 kv, a hissing sound gives evidence of ionization of the air in
the immediate vicinity of the wire. This corona discharge provides
positive and negative ion pairs adjacent to the wire. If the wire is
positive, some of the positive ions are drawn out of this region and
migrate to the cylindrical outer wall. Thus, outside the corona
discharge region there is a unipolar conduction current of the type
postulated in Example 7.7.2. The ion mobility is typically (1
 2) x 10-4 (m/s)/(v/m), while the field is on the
order of 5 x 105 v/m, so the ion velocity (7.1.3) is in the
range of 50-100 m/s.
2) x 10-4 (m/s)/(v/m), while the field is on the
order of 5 x 105 v/m, so the ion velocity (7.1.3) is in the
range of 50-100 m/s.
Smoke particles, mixed with air rising through the cylinder, can
be seen to be removed from the gas within a second or so. Large
polyethylene particles dropped in from the top can be more readily
seen to collect on the walls. In a practical precipitator, the
collection electrodes are periodically rapped so that chunks of
the collected material drop into a hopper below.
Most of the time required to clear the air of smoke is spent by
the particle in migrating to the wall after it has been charged. The
charging time constant  i is typically only a few milliseconds.
i is typically only a few milliseconds.
This demonstration further emphasizes the contrast between the
behavior of a macroscopic particle when immersed in an Ohmic
conductor, as in the previous demonstration, and when subjected to
unipolar conduction. A particle immersed in a unipolar
"conductor" becomes charged. In a uniform Ohmic conductor, it can
only discharge.
7.8 Electroquasistatic Conduction Laws forInhomogeneous Materials
In this section, we extend the discussion of transients to situations
in which the electrical permittivity and Ohmic conductivity are
arbitrary functions of space.

Distributions of these parameters, as exemplified in Figs. 6.5.1 and
7.2.3, might be uniform, piece-wise uniform, or smoothly nonuniform.
The specific examples falling into these categories answer three
questions.
tend to accumulate when it disappears from a region having
uniform properties.
| (a) | Where does the unpaired charge density, found in Sec. 7.7,
|
| (b) | With the unpaired charge
density determined by the self-consistent EQS laws, what is the
equation governing the potential distribution throughout the volume of
interest?
|
| (c) | What boundary and initial conditions make the solutions
to this equation unique?
|
The laws studied in this section and exemplified in the next describe
both the perfectly insulating limit of Chap. 6 and the conduction
dominated limit of Secs. 7.1-7.6. More important, as suggested in
Sec. 7.0, they describe how these limiting situations are related in
EQS systems.
Evolution of Unpaired Charge Density
With a nonuniform conductivity
distribution, the statement of charge conservation and Ohm's law
expressed by (7.7.1) becomes
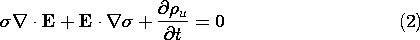
Similarly, with a nonuniform permittivity, Gauss' law as given by
(7.7.2) becomes

Elimination of 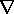
 E between these equations gives an
expression that is the generalization of the charge relaxation
equation, (7.7.3).
E between these equations gives an
expression that is the generalization of the charge relaxation
equation, (7.7.3).
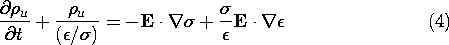
Wherever the electric field has a component in the direction of a
gradient of  or
or  , the unpaired charge density can be present
and can be temporally increasing or
decreasing. If a steady state has been established, in the sense that
time rates of change are negligible, the charge distribution is given
by (4), because then,
, the unpaired charge density can be present
and can be temporally increasing or
decreasing. If a steady state has been established, in the sense that
time rates of change are negligible, the charge distribution is given
by (4), because then, 
 u /
u /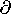 t = 0. Note that this is the
distribution of (7.2.8) that prevails for steady conduction.
We can therefore expect that the charge density found to disappear
from a region of uniform properties in Sec. 7.7 will reappear at
surfaces of discontinuity of
t = 0. Note that this is the
distribution of (7.2.8) that prevails for steady conduction.
We can therefore expect that the charge density found to disappear
from a region of uniform properties in Sec. 7.7 will reappear at
surfaces of discontinuity of  and
and  or in regions where
or in regions where  and
and  vary smoothly.
vary smoothly.
Electroquasistatic Potential Distribution
To evaluate (4), the self-consistent electric field intensity is
required. With the objective of determining that field, Gauss' law,
(7.7.2), is used to eliminate  u from the charge conservation
statement, (7.7.1).
u from the charge conservation
statement, (7.7.1).
For the first time in the analysis of charge relaxation, we now
introduce the electroquasistatic approximation
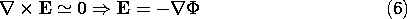
and (5) becomes the desired expression governing the evolution of
the electric potential.
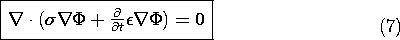
Uniqueness
Consider now the initial and boundary conditions that make solutions
to (7) unique. Suppose that throughout the volume V, the initial
charge distribution is given as

and that on the surface S enclosing this volume, the potential is a
given function of time
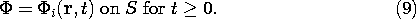
Thus, when t = 0, the initial distribution of electric field
intensity satisfies Gauss' law. The initial potential distribution
satisfies the same law as for regions occupied by perfect dielectrics.

Given the boundary condition of (9) when t = 0, it follows from
Sec. 5.2 that the initial distribution of potential is uniquely
determined.
Is the subsequent evolution of the field uniquely determined by
(7) and the initial and boundary conditions? To answer this
question, we will take a somewhat more formal approach than used in
Sec. 5.2 but nevertheless use the same reasoning. Supose that there
are two solutions,  =
=  a and
a and  =
=  b, that satisfy
(7) and the same initial and boundary conditions.
b, that satisfy
(7) and the same initial and boundary conditions.
Equation (7) is written first with  =
=  a and then with
a and then with
 =
=  b. With
b. With  d \equiv
d \equiv  a -
a -  b, the
difference between these two equations becomes
b, the
difference between these two equations becomes
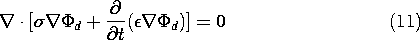
Multiplication of (11) by  d and integration over the volume
V gives
d and integration over the volume
V gives
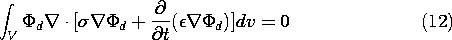
The objective in the following manipulation is to turn this
integration either into one over positive definite quantities or into
an integration over the surface S, where the boundary conditions
determine the potential. The latter is achieved if the integrand can
be expressed as a divergence. Thus, the vector identity
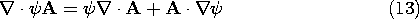
is used to write (12) as
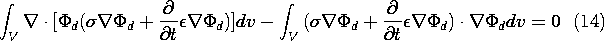
and then Gauss' theorem converts the first integral to one
over the surface S enclosing V.
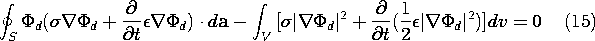
The conversion of (12) to (15) is an example of a
three-dimensional integration by parts. The surface integral is
analogous to an evaluation at the endpoints of a one-dimensional
integral.
If both  a and
a and  b satisfy the same condition on S,
namely (9), then the difference potential is zero on S for all 0
b satisfy the same condition on S,
namely (9), then the difference potential is zero on S for all 0
 t. Thus, the surface integral in (15) vanishes. We are left
with the requirement that for 0
t. Thus, the surface integral in (15) vanishes. We are left
with the requirement that for 0  t,
t,
Because both  a and
a and  b satisfy the same initial
conditions,
b satisfy the same initial
conditions,  d must initially be zero. Thus, for
d must initially be zero. Thus, for
 d to change to a nonzero
value from zero, the derivative on the left must be positive.
However, the integral on the right can only be zero or negative.
Thus,
d to change to a nonzero
value from zero, the derivative on the left must be positive.
However, the integral on the right can only be zero or negative.
Thus,  d must stay zero for all time. We conclude that the
fields found using (7), the initial condition of (8), and boundary
conditions of (9) are unique.
d must stay zero for all time. We conclude that the
fields found using (7), the initial condition of (8), and boundary
conditions of (9) are unique.
7.9 Charge Relaxation in Uniform and Piece-Wise UniformSystems
Configurations composed of subregions where the material has
uniform properties are already familiar from Secs. 6.6 and 7.5. The
conductivity and permittivity are then step functions of position, and
the terms on the right in (7.8.4) are spatial impulses. Thus, the
charge density tends to accumulate at interfaces between regions and
is represented by a surface charge density.
We consider first the evolution of the potential distribution in
a region having uniform properties. With the inhomogeneities
represented by the continuity conditions, the discussion is then
extended to piece-wise uniform configurations.
Fields in Regions Having Uniform Properties
Where  and
and  are uniform, (7.8.7) becomes
are uniform, (7.8.7) becomes

This expression is satisfied either if the potential obeys the
relaxation equation

or if it satisfies Laplace's equation

In general, the potential is a linear combination of these solutions.

The potential satisfying (2) is that associated with the relaxation
of the charge density initially distributed in the volume of the
material. We can think of this as being a particular solution, because
the divergence of the associated electric displacement D =  E =
-
E =
-
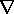
 p gives the unpaired charge density, (7.7.4), at each
point in the volume V for t > 0. The solutions
p gives the unpaired charge density, (7.7.4), at each
point in the volume V for t > 0. The solutions  h to
Laplace's equation can then be used to make the sum of the two solutions
satisfy the boundary conditions.
h to
Laplace's equation can then be used to make the sum of the two solutions
satisfy the boundary conditions.
Given that the initial charge density throughout the volume is  i
(r), the subsequent distribution is given by (7.7.4). One
particular solution for the potential that then satisfies
Poisson's equation throughout the volume follows from evaluating the
superposition integral [(4.5.3) with
i
(r), the subsequent distribution is given by (7.7.4). One
particular solution for the potential that then satisfies
Poisson's equation throughout the volume follows from evaluating the
superposition integral [(4.5.3) with  o
o 
 ] over that
volume.
] over that
volume.
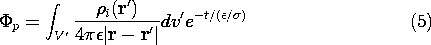
Note that this potential indeed satisfies (2) and the initial
conditions on the charge density in the volume. Of course, the
integral could be extended to charges outside the volume V, and the
particular solution would be equally valid.
The solutions to Laplace's equation make it possible to make the
total potential satisfy boundary conditions. Because an initial
distribution of volume charge density cannot be initiated by means of
boundary electrodes, the decay of an initial charge density is not
usually of interest. The volume potential is most often simply a
solution to Laplace's equation. Before delving into these more common
examples, consider one that illustrates the more general situation.
Example 7.9.1. Potential Associated with Relaxation of Volume
Charge
In Example 7.7.1, the decay of charge having a spherical
distribution in space was described. This could be done without
regard for boundary constraints. To determine the associated
potential, we stipulate the nature of the boundary surrounding the
uniform material in which the charge is initially embedded.
The uniform material fills the upper half-space and is bounded in
the plane z = 0 by a perfect conductor constrained to zero potential.
As shown in Fig. 7.9.1, when t = 0, there is an initial distribution of
charge density that is uniform and of density  o throughout a
spherical region of radius a centered at z = h on the z axis,
where h > a.
o throughout a
spherical region of radius a centered at z = h on the z axis,
where h > a.

In terms of a spherical coordinate system centered on the z axis
at z = h, a particular solution for the potential follows from the
integral form of Gauss' law, much as in Example 1.3.1. With r+
denoting the radial distance from the center of the spherical region,
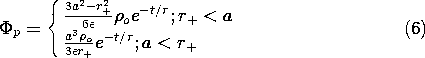
where r+ = [x2 + y2 + (z - h)2]1/2 and  \equiv
\equiv  /
/ .
.
Note that this potential satisfies (2) and the initial condition but
does not satisfy the zero potential condition at z = 0. To satisfy the
latter, we add a potential that is a solution to Laplace's equation,
(3), everywhere in the upper half-space. This is the potential
associated with an image charge density - o exp (-t/
o exp (-t/ )
distributed uniformly over a spherical region of radius a centered
at z = -h.
)
distributed uniformly over a spherical region of radius a centered
at z = -h.

where r- = [x2 + y2 + (z + h)2]1/2, \quad z > 0.
Thus, the total potential  =
=  p +
p +  h that satisfies
both the initial conditions and boundary conditions for 0 < t is
h that satisfies
both the initial conditions and boundary conditions for 0 < t is
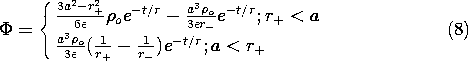
At each instant in time, the potential distribution is the same as if
the charge and its image were static. As the charge relaxes, so does
its image. Note that the charge relaxes to the boundary without
producing a net charge density anywhere outside the spherical region
where the charge was initiated.
Continuity Conditions in Piece-Wise Uniform Systems
Where the material properties undergo step discontinuities, the
differential equations are represented by continuity conditions. The
one representing the condition that the field be irrotational,
(7.8.6), is the same as that in Sec. 5.3.
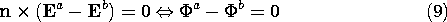
The continuity condition representing Gauss' law, (7.7.2), is also
familiar (6.2.16).
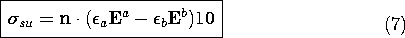
The continuity condition representing charge conservation, (7.7.1),
is (1.5.12). With the current density expressed in terms of Ohm's
law, this continuity condition becomes
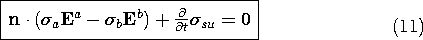
For the incremental volume of Fig. 7.9.2, this continuity condition
requires that if the conduction current entering the volume from
region (b) exceeds that leaving to region (a), there must be an
increasing surface charge density within the volume.

The fact that we are solving a second-order differential equation,
(7.8.7), suggests that there are really only two continuity
conditions. Thus, Gauss' continuity condition only serves to relate
the field to the unknown surface charge density, and the combination
of (10) and (11) comprise one continuity condition.
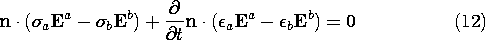
This continuity condition and the one on the tangential field or
potential, (9), are needed to splice together solutions
representing fields in piece-wise uniform configurations.
The following example illustrates how the time
dependence of the continuity condition allows the fields and charge
distribution to evolve from the distributions for perfect dielectrics
described in the latter part of Chap. 6 to the steady conduction
distributions discussed in the first part of this chapter.
Example 7.9.2. Maxwell's Capacitor
A configuration that brings out the roles of polarization and
conduction in the field evolution while avoiding geometric complications
is shown in Fig. 7.9.3. The space between perfectly conducting parallel
plates is filled by layers of material. The one above has thickness a,
permittivity  a, and conductivity
a, and conductivity  a, while for the one
below, these parameters are b,
a, while for the one
below, these parameters are b,  b, and
b, and  b, respectively.
When t = 0, a switch is closed and the potential V of a battery
is applied across the two electrodes. Initially, there is no
unpaired charge between the electrodes either in the volume or on the
interface.
b, respectively.
When t = 0, a switch is closed and the potential V of a battery
is applied across the two electrodes. Initially, there is no
unpaired charge between the electrodes either in the volume or on the
interface.

The electrodes are assumed long enough so that the fringing can be
neglected and the fields in each of the materials taken as uniform.
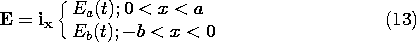
The linear potential associated with this distribution satisfies
Laplace's equation, (3). Because there is no initial charge density
in the volumes of the layers, the particular part of the potential,
the solution to (2), is zero.
The voltage source imposes the condition that the line
integral of the electric field between the plates must be equal to
v(t).
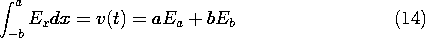
Because the layers are conducting, they respond to the
application of the voltage with conduction currents. Since the
currents differ, they cause a time rate of change of unpaired surface
charge density at the interface between the layers, as expressed by
(12).
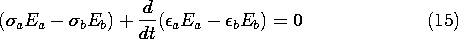
Note that the boundary conditions on tangential E at the electrode
surfaces and at the interface are automatically satisfied.
Given the driving voltage, these last two expressions comprise two
equations in the two unknowns Ea and Eb. Thus, the solution to
(14) for Eb and substitution into (15) gives a first-order
differential equation for the field response in the upper layer.
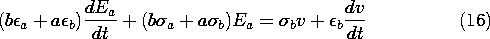
In particular, consider the response to a step in voltage, v = V
u-1(t). The drive on the right in (16) then consists of a step
and an impulse. The impulse must be matched by an impulse on the
left. That is, the field Ea also undergoes a step change when t = 0.
To identify the magnitude of this step, integrate (16) from 0- to
0+.
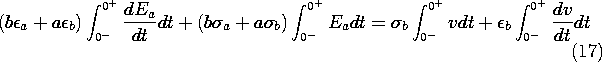
The result is a relationship between the jumps in voltage and in
field.
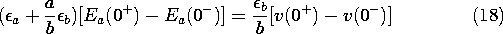
Because v(0-) = 0 and Ea(0-) = 0, it follows that

For t > 0, the particular plus homogeneous solution to (16) is
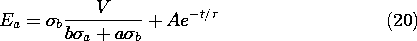
where
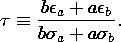
The coefficient A is adjusted to make Ea meet the initial condition
given by (19). Thus, the field transient in the upper layer is
found to be
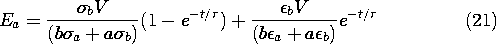
It follows from (14) that the field in the lower layer is then

The unpaired surface charge density, (10), follows from these fields.
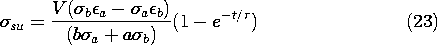
The field and unpaired surface charge density transients are shown
in Fig. 7.9.4. The curves are drawn to depict a lower layer that has a
somewhat greater permittivity and a much greater conductivity than the
upper layer. Just after the step in voltage, when t = 0+, the surface
charge density remains zero. Thus, the electric fields are at first
what they would be if the layers were regarded as perfectly insulating
dielectrics. As the surface charge accumulates, these fields approach
values consistent with steady conduction. The limiting surface charge
density approaches a saturation value that could be found by first
evaluating the steady conduction fields and then finding
 su.
Note that this surface charge can be positive or negative. With the
lower region much more conducting than the upper one (
su.
Note that this surface charge can be positive or negative. With the
lower region much more conducting than the upper one ( b
b  a
\gg
a
\gg  a
a b) the surface charge is positive. In this case, the
field ends up tending to be shielded out of the lower layer.
b) the surface charge is positive. In this case, the
field ends up tending to be shielded out of the lower layer.

Piece-wise continuous configurations can often be represented by
capacitor-resistor networks. An exact circuit representation of
Maxwell's capacitor is shown in Fig. 7.9.5. The voltages across the
capacitors are simply va = Ea a and vb = Eb b. In the
circuit, the surface charge density given by (23) is the sum of the
net charge per unit area on the lower plate of the top capacitor and
that on the upper plate of the lower capacitor.

Nonuniform Fields in Piece-Wise Uniform Systems
We continue now to consider examples with no initial charge
density in the regions having uniform conductivity and dielectric
constant. Since it is not
possible to establish a charge density in these regions by means of
boundary constraints, this is almost always the situation in practice.
The field distributions in the uniform subregions have
potentials that satisfy Laplace's equation, (3). These are
"spliced" together at the interfaces between regions and constrained
at boundaries by conditions that vary with time. The continuity
conditions vary with time to account for the accumulation of unpaired
charge at the interfaces between regions.
Maxwell's capacitor, Example 7.9.2, illustrates most features of
the surface charge relaxation process. The response to a step
function of voltage across an electrode pair is at first the field
distribution of a system of perfect dielectrics, as developed in Chap.
6. After many charge relaxation times, steady conduction prevails, and
the fields are as described in Sec. 7.5. In the remainder of this
section, configurations will be considered that, by contrast to
Maxwell's capacitor, have fields that change their shape as the
relaxation process evolves.
The interplay of polarization and conduction processes is also
evident in the sinusoidal steady state response of a system. Just as
the Maxwell capacitor has short-time and long-time responses dominated
by the "capacitors" and "resistors," respectively, the high-frequency
and low-frequency responses are dominated by polarization and
conduction, respectively. This too will now be illustrated.
Example 7.9.3. Spherical Semi-insulating Material Embedded in a
Second Material Stressed by Uniform Electric Field
An electric field
intensity E(t) is imposed on a material having permittivity
and conductivity ( a ,
a ,  a),
perhaps by means of plane parallel electrodes. At the origin of a
spherical coordinate
system embedded in this material is a spherical region having
permittivity and conductivity (
a),
perhaps by means of plane parallel electrodes. At the origin of a
spherical coordinate
system embedded in this material is a spherical region having
permittivity and conductivity ( b ,
b ,  b) and radius R,
as shown in Fig. 7.9.6. Limiting
cases include a conducting sphere surrounded by free space
(
b) and radius R,
as shown in Fig. 7.9.6. Limiting
cases include a conducting sphere surrounded by free space
( a =
a =  o ,
o ,  a = 0)
or an insulating spherical cavity surrounded by a
conducting material (
a = 0)
or an insulating spherical cavity surrounded by a
conducting material ( b = 0).
b = 0).

In each of the regions, the potential must satisfy Laplace's
equation. From our experience with the potentials for perfect dielectric
and for steady conduction configurations, we can expect
that the boundary conditions can be satisfied using combinations of
uniform and dipole fields. With the understanding that the
coefficients A(t) and B(t) are functions of time, the solutions to
Laplace's equation are therefore postulated to take the form
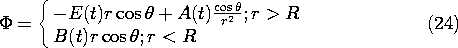
Note that the uniform part of the exterior field has been matched at
r 
 to the given driving field.
to the given driving field.
Continuity of the tangential electric field at r = R, (9),
requires that these potential functions match at r = R.

Conservation of charge, with the surface charge density represented
using Gauss' law, (12), makes the further requirement that
In substituting the potentials of (24) into these two conditions, no
derivatives with respect to 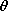 are taken, so each term has the
are taken, so each term has the
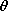 dependence cos (
dependence cos (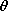 ).
It is for this reason that such a simple solution
can be used to satisfy the continuity conditions. Substitution into
(25) relates the coefficients
).
It is for this reason that such a simple solution
can be used to satisfy the continuity conditions. Substitution into
(25) relates the coefficients
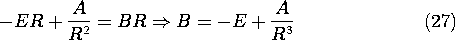
and with this relation used to eliminate B, substitution into (26)
results in a differential equation for A(t), with E(t) as a driving
function.
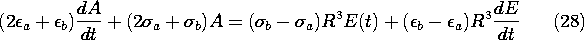
Step Response
Note that expression (28) has the same form as that for
Maxwell's capacitor, (16). The procedure leading to the
field response to a step function of applied field, E = Eo
u-1(t), is
therefore identical to that illustrated in Example 7.9.2. In fact,
comparison of these equations makes it clear that the required
solution, given that there were no initial fields (when t = 0-), is
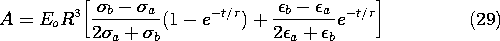
where the relaxation time  = (2
= (2 a +
a +  b)/(2
b)/(2 a +
a +
 b). The coefficient B follows from (27). Thus, the
potential of (24) is determined for t \geq 0.
b). The coefficient B follows from (27). Thus, the
potential of (24) is determined for t \geq 0.
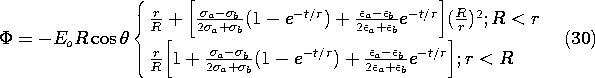
The accumulation of unpaired surface charge at r = R
accounts for the redistribution of potential with time. It follows
from (10) that
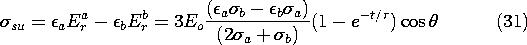
Thus, the unpaired surface charge density accumulates at the poles of
the sphere, exponentially approaching a saturation value at a rate
determined by the relaxation time  . Just after the field
is turned on, this surface charge density is zero and the field
distribution should be that for a uniform field applied to perfect
dielectrics. Indeed, evaluated when t = 0, (30) gives the potential
for perfect dielectrics. In the opposite extreme, where many
relaxation times have passed so that the exponentials in (30) are
negligible, the potential assumes the distribution for steady
conduction.
. Just after the field
is turned on, this surface charge density is zero and the field
distribution should be that for a uniform field applied to perfect
dielectrics. Indeed, evaluated when t = 0, (30) gives the potential
for perfect dielectrics. In the opposite extreme, where many
relaxation times have passed so that the exponentials in (30) are
negligible, the potential assumes the distribution for steady
conduction.
A graphical portrayal of this field transient is given in Fig.
7.9.7. The case shown was chosen because it involves a drastic
redistribution of the field as time progresses. The spherical region
is highly conducting compared to its surroundings, but the exterior
material is highly polarizable compared to the spherical region.
Thus, just after the switch is closed, the field lines tend to be
trapped in the outer region. As time progresses and conduction rules,
these lines tend to pass through the highly conducting sphere. The
temporal scale of the transient is determined by the relaxation time
 .
.

Sinusoidal Steady State Response
Consider now the sinusoidal steady state that results from applying
the uniform field
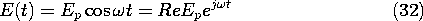
As in dealing with ac circuits, where the currents and voltages are
also solutions to constant coefficient ordinary differential
equations, the response is now assumed to have the same frequency
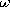 as
the drive but to have a yet to be determined amplitude and phase
represented by the complex coefficients A and B.
as
the drive but to have a yet to be determined amplitude and phase
represented by the complex coefficients A and B.
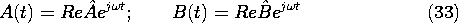
Substitution of (32) and (33a) into (28) gives an expression that can
be solved for \hat A in terms of the drive, Ep.
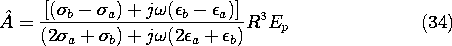
In turn, the complex amplitude B follows from this result and (27).
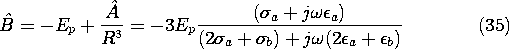
Now, with the amplitudes in (31) and (32) given by these
expressions, the sinusoidal steady state fields postulated with
(24) are determined.
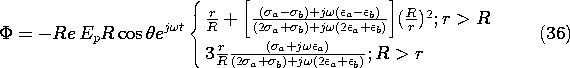
The surface charge density associated with these fields is then
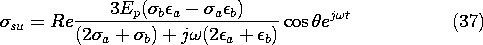
With the frequency rather than the time as the parameter, these
expressions can be interpreted analogously to the step function
response, (30) and (31). In the high-frequency limit, where
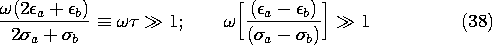
the conductivity terms become negligible in (36), the coefficients
\hat A and \hat B become independent of frequency and real.
Thus, the fields are
in temporal phase with the applied field and sinusoidally varying
versions of what would be found if the materials were assumed to be
perfect dielectrics. If the frequency is high compared to the
reciprocal charge relaxation times, the field distributions are
the same as they would be just after a step in applied field [when
t = 0+ in (30)].
With the inequalities of (38) reversed, the terms involving the
permittivity in (36) are negligible, the coefficients \hat A and
\hat B are
again real and hence the fields are just as they would be for
stationary conduction except that they vary sinusoidally with time.
Thus, in the low frequency limit, the fields are sinusoidally varying
versions of the steady conduction fields that prevail long after a
step in applied field [(30) in the limit t 
 ].
].
These high- and low-frequency limits are consistent with the
frequency dependence of the unpaired surface charge density, given by
(37). At low frequencies, this surface charge density varies
sinusoidally in or out of phase with the applied field and with an
amplitude consistent with steady conduction. As the frequency is made
to greatly exceed the reciprocal relaxation time, the magnitude of
this charge falls to zero. In this high-frequency limit, there is
insufficient time during one cycle for significant charge to relax to
the spherical interface. Thus, at high frequencies the fields become
the same as if the unpaired charge density were ignored and the
dielectrics assumed to be perfectly insulating.
In the two demonstrations that close this section, an obvious
objective is the association of the previous example with practical
situations. The approximations used to rederive the relevant fields
cast further light on the physical processes at work.
\begindemo1Capacitively Induced Fields in a Person in the Vicinity
of a High-Voltage Power Line
A person standing under a conventional power line, as in Fig.
7.9.8a, is subject to a 60 Hz alternating electric field intensity
that is typically 5 x 104 v/m. In response to this field,
body currents
are induced. Common experience suggests that these are not large
enough to create discomfort, but are the currents appreciable enough to
be of long-term medical concern?

In the bare-handed maintenance of power lines, a person is
brought to within arms length of the line by an insulated hoist, as
shown in Fig. 7.9.8b. Without shielding, the body is in this case
subjected to much more intense fields, perhaps 5 x 105 v/m.
For the first person proving out this technique, the estimation of
fields and currents within the body was of considerable interest.
To the layman, these imposed fields seem to imply that a body one
meter in length would be subject to a voltage difference of 50 kV at
the ground and 500 kV near the line. However, as we will now
illustrate, surrounded by air, the body does an excellent job of
shielding out the electric field.
The hemispherical conductor resting on a ground plane, shown in
Fig. 7.9.9, is a model for an individual on (and in electrical
contact with) the ground. In the experiment, the
hemisphere is jello, molded to have the radius R and having a
conductivity essentially that of the salt water used in its making.
(To obtain the physiological conductivity of 0.2 S/m, unflavored
gelatine is made using 0.02 M NaCl, a solution of 1.12 grams/liter.)

Presumably, the potential in and around the hemisphere is given by
(30). The z = 0 plane is at zero potential for the spherical region
described, and so the potential applies equally well to the hemisphere
on the ground plane. Parameters are ( a,
a,  a) = (
a) = ( o , 0)
in the air and (
o , 0)
in the air and ( b,
b,  b) = (
b) = ( ,
,  ) in the hemisphere.
A conductivity typical of physiological tissue is
) in the hemisphere.
A conductivity typical of physiological tissue is  = .2
S/m. As a result, the charge relaxation time based on the
permittivity of the body (
= .2
S/m. As a result, the charge relaxation time based on the
permittivity of the body ( b = 81
b = 81 o) and the conductivity of the
body is extremely short,
o) and the conductivity of the
body is extremely short,  = 4 x 10-9 s. This makes it
possible to approximate the potential distribution using the two
simple steps that follow.
= 4 x 10-9 s. This makes it
possible to approximate the potential distribution using the two
simple steps that follow.
First, because the charge can relax to the surface in a time that
is far shorter than 1/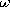 , and because the hemisphere is
surrounded by material that has far less conductivity, as far as
the field in the air is concerned, its surface is an equipotential.
, and because the hemisphere is
surrounded by material that has far less conductivity, as far as
the field in the air is concerned, its surface is an equipotential.

Thus, the potential distribution can be written by inspection [or by
recourse to (5.9.7)] as
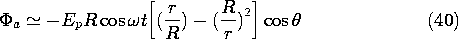
Because of the short relaxation time and high conductivity for the
sphere relative to the air, the surface charge density is essentially
determined by the exterior field. Thus,
the conservation of charge continuity condition, (12), is approximately
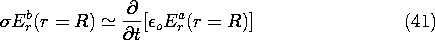
The rate of change of the surface charge density on the right in this
expression has already been determined, so the expression serves to
evaluate the normal conduction current density just inside the
hemispherical surface.
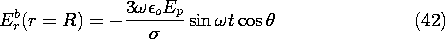
In the interior region, the potential is uniform and thus takes the
form Br cos ( ). Evaluation of the coefficient B by using
(42) then
gives the approximate potential distribution within the hemisphere.
). Evaluation of the coefficient B by using
(42) then
gives the approximate potential distribution within the hemisphere.
In retrospect, note that the potentials given by (40) and (43)
are obtained by taking the appropriate limit of the potential obtained
without making approximations, (36).
Inside the
hemisphere, the conditions for essentially steady conduction prevail.
Thus, the potential predicted by (43) is probed by means of metal
spheres (Ag/AgCl electrodes) embedded in the jello and connected to an
oscilloscope through insulated wires. Inside the hemisphere, surface
charge stored on the surfaces of the insulated wires has a minor
effect on the current distribution.
Typical experimental values for a 250 Hz excitation are R = 3 .8 cm,
s = 12.7 cm, v = 565 V peak, and  = 0.2 S/m. With the
probes located at z = 2.86 cm and z = 0.95 cm,
the measured potentials are 25
= 0.2 S/m. With the
probes located at z = 2.86 cm and z = 0.95 cm,
the measured potentials are 25  V peak
and 10
V peak
and 10  V peak, respectively. With the given parameters, (43)
gives 26.5
V peak, respectively. With the given parameters, (43)
gives 26.5 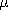 V peak and 8.8
V peak and 8.8 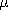 V peak, respectively.
V peak, respectively.
What are the typical current densities that would be induced in a
person in the vicinity of a power line? According to (41), for the
person on the ground in a field of 5 x 104 V/m
(Fig. 7.9.8a), the current density is Jz =  Ez = 0.05
Ez = 0.05
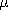 A/cm2. For the person doing bare-handed
maintenance where the field is perhaps 5 x 105 V/m (Fig.
7.9.8b), the
model is a sphere in a uniform field (Fig. 7.9.8d). The current
density is again given by (43), Jz =
A/cm2. For the person doing bare-handed
maintenance where the field is perhaps 5 x 105 V/m (Fig.
7.9.8b), the
model is a sphere in a uniform field (Fig. 7.9.8d). The current
density is again given by (43), Jz =  Ez = 0.5
Ez = 0.5 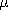 A/cm2.
A/cm2.
Of course, the geometry of a person is not spherical. Thus, it
can be expected that the field will concentrate more in the actual
situation than for the hemispherical or spherical models. The
approximations introduced in this demonstration would greatly simplify
the development of a numerical model.
Have we found estimates of current densities suggesting danger,
especially for the maintenance worker? Physiological systems are far
too complex for there to be a simple answer to this question. However,
matters are placed in some perspective by recognizing that currents of
diverse origins exist in the body so long as it lives. In the next
demonstration, electrocardiogram potentials are used to estimate
current densities that result from the muscular contractions of the
heart. The magnitude of the current density found there will lend some
perspective to that determined here.
The approximate analysis introduced in support of the previous
demonstration is an example of the "inside-outside" viewpoint
introduced in Sec. 7.5. The exterior insulating region, where the
field was applied, was "inside," while the interior conducting
region was "outside." The following demonstration continues this
theme with a contrasting example, where the excitation is in the
conducting region.
Demonstration 7.9.2. Currents Induced by the Heart
The configuration for taking an electrocardiogram is typically as
shown in Fig. 7.9.10. With care taken to balance out 60 Hz signals
induced in each of the electrodes by external fields, the electrical
signals induced by the muscle contractions in the heart are easily
measured using a conventional oscilloscope. In practice, many
electrodes are used so that detailed information on the
distribution of the muscle contractions can be discerned.

Here we simply represent the heart by a dipole source of
current at the center of a conducting sphere, somewhat as depicted in
Figs. 7.9.10 and 7.9.11. Relatively little current is induced in the
limbs, so that potentials measured at the extremities roughly reflect
the potentials on the surface of the equivalent sphere. Given that
typical potential differences are on the order of millivolts, what current
dipole moment can we attribute to the heart, and what are the typical
current densities in its neighborhood?
With the heart represented by a current source of dipole moment ip d
at the center of the spherical "torso," the electric potential at
the origin approaches that for the dipole current source, (7.3.9).
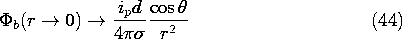

At the surface r = R, the spherical body is being surrounded by an
insulator. Thus, again using Fig. 7.9.11, any normal conduction
current must be accounted for by the accumulation of surface charge.
Because the relaxation time is so short compared to the 1 s period
typical of the heart, the current density associated with the buildup
of surface charge is extremely small. As a result, the current
distribution inside the sphere is as though the normal current density
at r = R were zero.

Thus, the potential within the body is fully determined without regard
for constraints from the surrounding region. The solution to
Laplace's equation that satisfies these last two conditions is
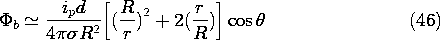
Because the potential is continuous at r = R, the potential on the
surface of the "torso" follows from evaluation of this expression at
r = R.
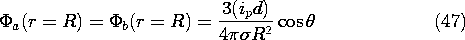
Thus, given that the potential difference between  = 45
degrees and
= 45
degrees and 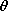 = 135 degrees is 1 mV, that R = 25 cm, and
that
= 135 degrees is 1 mV, that R = 25 cm, and
that  = 0.2 S/m, it follows from (47) that the peak current
dipole moment of the heart is 3.7 x 10-5 A - m.
= 0.2 S/m, it follows from (47) that the peak current
dipole moment of the heart is 3.7 x 10-5 A - m.
Typical current densities can now be found using (46) to
evaluate the electric field intensity. For example, the current
density at the radius R/2 just above the dipole source is
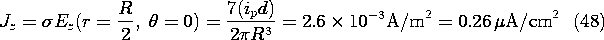
Note that at the particular position selected the current density
exceeds with some margin that to which the maintenance worker is
subjected in the previous demonstration.
To begin to correlate the state and function of the heart with
electrocardiograms, it is necessary to represent the heart by a
current dipole that not only has a special temporal signature but
rotates with time as well[1,2]. Unfortunately, much of the medical
literature on the subject takes the analogy between electric dipoles
(Sec.4.4) and current dipoles (Sec. 7.3) literally. The heart is
described as an electric dipole[2], which it certainly is not. If it
were, its fields would be shielded out by the surrounding conducting
flesh.
 .
.
 u and
u and
 p, which, respectively, represented unpaired and paired charges.
The paired charges were related to the polarization density P
with the result that Gauss' law could be written as (6.2.15)
p, which, respectively, represented unpaired and paired charges.
The paired charges were related to the polarization density P
with the result that Gauss' law could be written as (6.2.15)

 o E + P. Throughout Chap. 6, the volume
was assumed to be perfectly insulating. Thus,
o E + P. Throughout Chap. 6, the volume
was assumed to be perfectly insulating. Thus,  p was either
zero or a given distribution.
The second step toward a self-consistent description of the
volume charge density is taken by adding to (1) and (2) an equation
expressing conservation of the unpaired charges, (2.3.3).
p was either
zero or a given distribution.
The second step toward a self-consistent description of the
volume charge density is taken by adding to (1) and (2) an equation
expressing conservation of the unpaired charges, (2.3.3).

 E.
E.


 , the capacitors cease charging and are
equivalent to open circuits. The distribution of voltages is then
determined by the steady flow of current through the resistors. In
this long-time limit, the charge on the capacitors is determined from
the voltages already specified by the resistive network.
, the capacitors cease charging and are
equivalent to open circuits. The distribution of voltages is then
determined by the steady flow of current through the resistors. In
this long-time limit, the charge on the capacitors is determined from
the voltages already specified by the resistive network.
 u /
u / t\
t\  0 in the
conservation of
charge expression, (3). We will find that (1) and (3), the latter
written with Ju represented by the conduction constitutive
law, then fully determine the distribution of potential, of E, and
hence of Ju. Just as the charges on the capacitors in the
circuit of Fig. 7.0.1b are then specified by the already determined
voltage distribution, the charge distribution can be found in an
after-the-fact fashion from the already determined field distribution
by using Gauss' law, (2). After considering the physical basis for
common conduction constitutive laws in Sec. 7.1, Secs. 7.2-7.6 are
devoted to steady conduction phenomena.
0 in the
conservation of
charge expression, (3). We will find that (1) and (3), the latter
written with Ju represented by the conduction constitutive
law, then fully determine the distribution of potential, of E, and
hence of Ju. Just as the charges on the capacitors in the
circuit of Fig. 7.0.1b are then specified by the already determined
voltage distribution, the charge distribution can be found in an
after-the-fact fashion from the already determined field distribution
by using Gauss' law, (2). After considering the physical basis for
common conduction constitutive laws in Sec. 7.1, Secs. 7.2-7.6 are
devoted to steady conduction phenomena.

 .
.
 B/
B/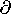 t is negligible in an MQS system, Faraday's law again reduces to
(1). Thus, the first half of this chapter provides an understanding
of steady conduction in some MQS as well as EQS systems. In Chap. 8,
we determine the
magnetic field intensity from a given distribution of current
density. Provided that rates of change are slow enough so that
effects of magnetic induction can be ignored, the solution to the
steady conduction problem as addressed in Secs. 7.2-7.6 provides the
distribution of the magnetic field source, the current density,
needed to begin Chap. 8.
t is negligible in an MQS system, Faraday's law again reduces to
(1). Thus, the first half of this chapter provides an understanding
of steady conduction in some MQS as well as EQS systems. In Chap. 8,
we determine the
magnetic field intensity from a given distribution of current
density. Provided that rates of change are slow enough so that
effects of magnetic induction can be ignored, the solution to the
steady conduction problem as addressed in Secs. 7.2-7.6 provides the
distribution of the magnetic field source, the current density,
needed to begin Chap. 8.


 \pm
are positive
constants representing the time average "drag" resulting from
collisions of the carriers with the fixed atoms or molecules through
which they move.
\pm
are positive
constants representing the time average "drag" resulting from
collisions of the carriers with the fixed atoms or molecules through
which they move.
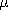 \pm,
the velocities of the positive and negative particles follow from
(2) as
\pm,
the velocities of the positive and negative particles follow from
(2) as

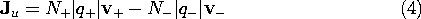
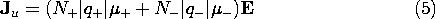

 .
.
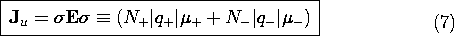



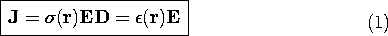


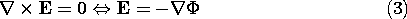




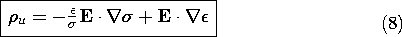

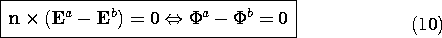

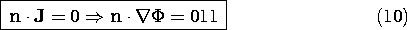
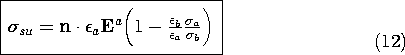

 da over
the surface S. This integral law is then applied to the surface shown
in Fig. 7.2.1 enclosing the electrode that is connected to the
positive terminal. Where it intersects the wire, the contribution is
-i, so that the integral over the closed surface becomes
da over
the surface S. This integral law is then applied to the surface shown
in Fig. 7.2.1 enclosing the electrode that is connected to the
positive terminal. Where it intersects the wire, the contribution is
-i, so that the integral over the closed surface becomes

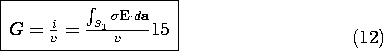

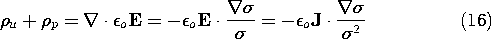
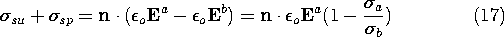
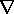



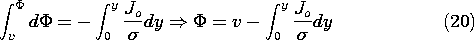
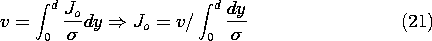
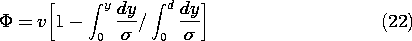




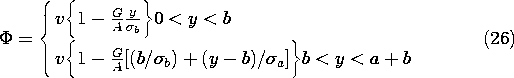




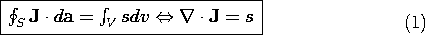

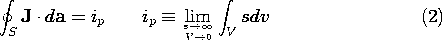



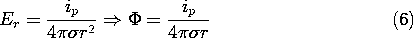

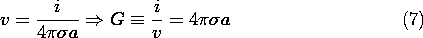







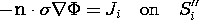

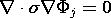
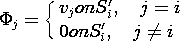

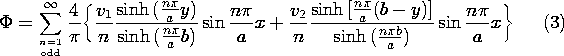

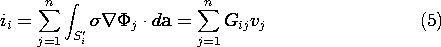


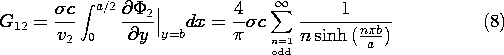




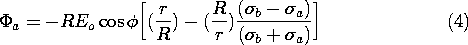
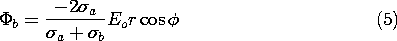

 and also having conductivity
and also having conductivity 





 dependence, Laplace's equation
requires that
dependence, Laplace's equation
requires that
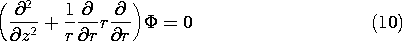

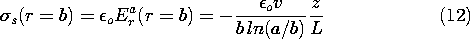

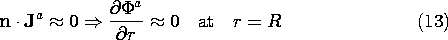
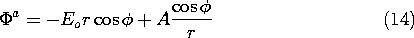
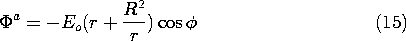

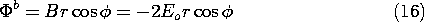
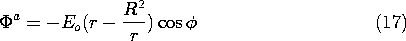
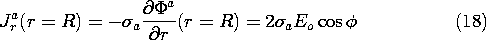


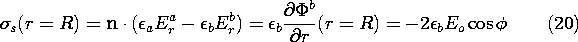


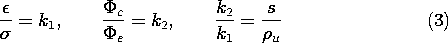
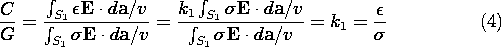

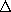 n and the distance between E lines is
n and the distance between E lines is 

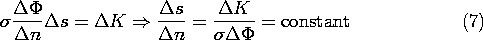

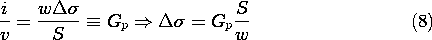

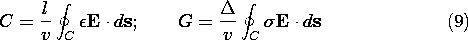





 e
has the typical values illustrated in Table 7.7.1.
e
has the typical values illustrated in Table 7.7.1.


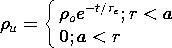





 \geq
\geq 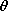 \geq
\geq 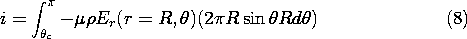
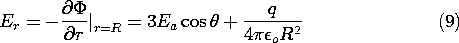
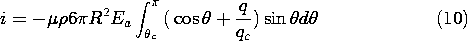


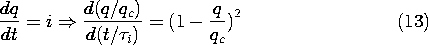
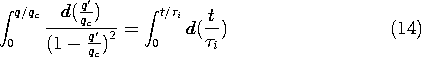




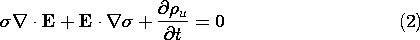

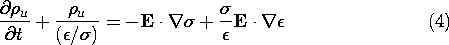
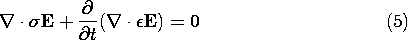
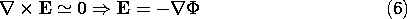
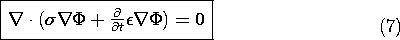

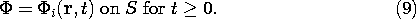

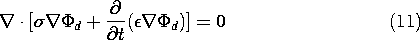
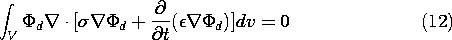
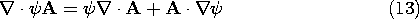
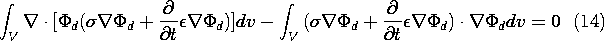
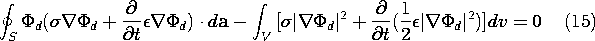
 t. Thus, the surface integral in (15) vanishes. We are left
with the requirement that for 0
t. Thus, the surface integral in (15) vanishes. We are left
with the requirement that for 0 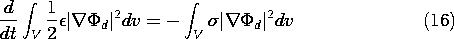




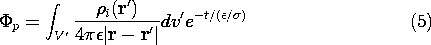

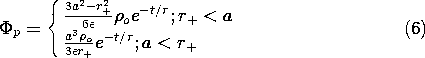

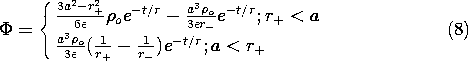
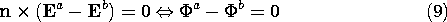
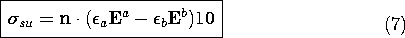
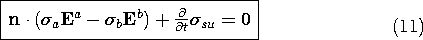

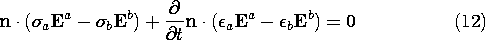

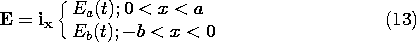
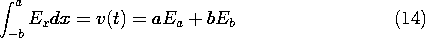
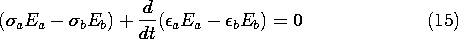
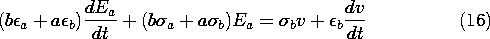
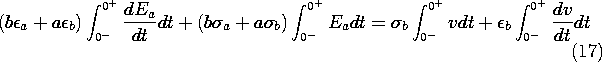
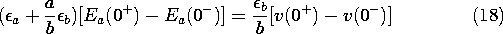

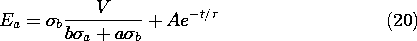
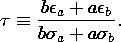
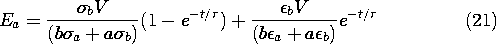

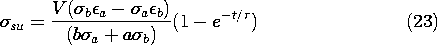



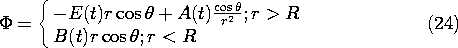

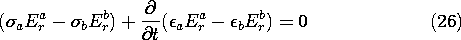
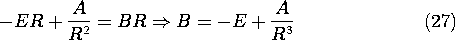
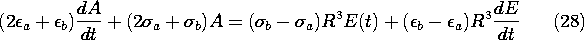
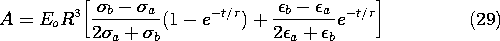
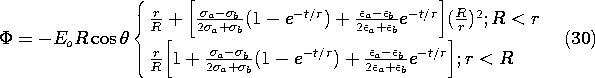
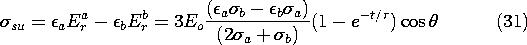

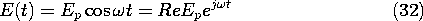
 as
the drive but to have a yet to be determined amplitude and phase
represented by the complex coefficients A and B.
as
the drive but to have a yet to be determined amplitude and phase
represented by the complex coefficients A and B.