We now follow the study of electroquasistatics with that of magnetoquasistatics. In terms of the flow of ideas summarized in Fig. 1.0.1, we have completed the EQS column to the left. Starting from the top of the MQS column on the right, recall from Chap. 3 that the laws of primary interest are Ampère's law (with the displacement current density neglected) and the magnetic flux continuity law (Table 3.6.1).


These laws have associated with them continuity conditions at interfaces. If the interface carries a surface current density K, then the continuity condition associated with (1) is (1.4.16)

and the continuity condition associated with (2) is (1.7.6).

In the absence of magnetizable materials, these laws determine the magnetic field intensity H given its source, the current density J. By contrast with the electroquasistatic field intensity E, H is not everywhere irrotational. However, it is solenoidal everywhere.
The similarities and contrasts between the primary EQS and MQS laws are the topic of this and the next two chapters. The similarities will streamline the development, while the contrasts will deepen the understanding of both MQS and EQS systems. Ideas already developed in Chaps. 4 and 5 will also be applicable here. Thus, this chapter alone plays the role for MQS systems taken by these two earlier chapters for EQS systems.
Chapter 4 began by expressing the irrotational E in terms of
a scalar potential. Here H is not generally irrotational,
although it may be in certain source-free regions. On the other
hand, even with
the effects of magnetization that are introduced in Chap. 9, the
generalization of the magnetic flux density 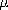 o H has no
divergence anywhere. Therefore, Sec. 8.1 focuses on the solenoidal
character of
o H has no
divergence anywhere. Therefore, Sec. 8.1 focuses on the solenoidal
character of 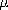 o H and develops a vector form of Poisson's
equation satisfied by the vector potential, from which the H field
may be obtained.
o H and develops a vector form of Poisson's
equation satisfied by the vector potential, from which the H field
may be obtained.
In Chap. 4, where the electric potential was used to represent an irrotational electric field, we paused to develop insights into the nature of the scalar potential. Similarly, here we could delve into the way in which the vector potential represents the flux of a solenoidal field. For two reasons, we delay developing this interpretation of the vector potential for Sec. 8.6. First, as we see in Sec. 8.2, the superposition integral approach is often used to directly relate the source, the current density, to the magnetic field intensity without the intetermediary of a potential. Second, many situations of interest involving current-carrying coils can be idealized by representing the coil wires as surface currents. In this idealization, all of space is current free except for some surfaces within which surface currents flow. But, because H is irrotational everywhere except through these surfaces, this means that the H field may be expressed as the gradient of a scalar potential. Further, since the magnetic field is divergence free (at least as treated in this chapter, which does not deal with magnetizable materials), the scalar potential obeys Laplace's equation. Thus, most methods developed for EQS systems using solutions to Laplace's equation can be applied to the solution to MQS problems as well. In this way, we find "dual" situations to those solved already in earlier chapters. The method extends to time-varying quasistatic magnetic fields in the presence of perfect conductors in Sec. 8.4. Eventually, in Chap. 9, we shall extend the approach to problems involving piece-wise uniform and linear magnetizable materials.
Vector Field Uniquely Specified
A vector field is uniquely specified by its curl and divergence. This fact, used in the next sections, follows from a slight modification to the uniqueness theorem discussed in Sec. 5.2. Suppose that the vector and scalar functions C(r) and D(r) are given and represent the curl and divergence, respectively, of a vector function F.


The same arguments used in this earlier uniqueness proof then shows that F is uniquely specified provided the functions C (r) and D(r) are given everywhere and have distributions consistent with F going to zero at infinity. Suppose that Fa and Fb are two different solutions of (5) and (6). Then the difference solution Fd = Fa - Fb is both irrotational and solenoidal.


The difference solution is governed by the same equations as in Sec. 5.2. With Fd taken to be the gradient of a Laplacian potential, the remaining steps in the uniqueness argument are equally applicable here.
The uniqueness proof shows the importance played by the two differential vector operations, curl and divergence. Among the many possible combinations of the partial derivatives of the vector components of F, these two particular combinations have the remarkable property that their specification gives full information about F.
In Chap. 4, we determined a vector field F = E given that
the vector source C = 0 and the scalar source D = 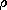 /
/ o.
In Secs. 8.1 we find the vector field F = H, given that
the scalar source D = 0 and that the vector source is C = J.
o.
In Secs. 8.1 we find the vector field F = H, given that
the scalar source D = 0 and that the vector source is C = J.
The strategy in this chapter parallels that for Chaps. 4 and 5. We can again think of dividing the fields into two parts, a particular part due to the current density, and a homogeneous part that is needed to satisfy boundary conditions. Thus, with the understanding that the superposition principle makes it possible to take the fields as the sum of particular and homogeneous solutions, (1) and (2) become




In sections 8.1-8.3, it is presumed that the current density is given everywhere. The resulting vector and scalar superposition integrals provide solutions to (9) and (10) while (11) and (12) are not relevant. In Sec. 8.4, where the fields are found in free-space regions bounded by perfect conductors, (11) and (12) are solved and boundary conditions are met without the use of particular solutions. In Sec. 8.5, where currents are imposed but confined to surfaces, a boundary value approach is taken to find a particular solution. Finally, Sec. 8.6 concludes with an example in which the region of interest includes a volume current density (which gives rise to a particular field solution) bounded by a perfect conductor (in which surface currents are induced that introduce a homogeneous solution).

