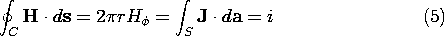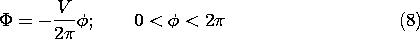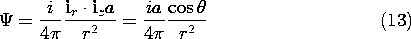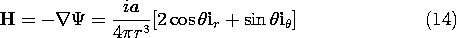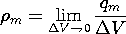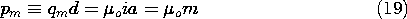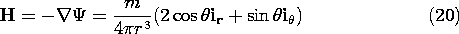The vector potential A describes magnetic fields that possess curl wherever there is a current density J (r). In the space free of current,

and thus H ought to be derivable there from the gradient of a potential.

Because

we further have

The potential obeys Laplace's equation.
Example 8.3.1. The Scalar Potential of a Line Current
A line current is a source singularity (at the origin of a polar coordinate system if it is placed along its z axis). From Ampère's integral law applied to the contour C of Fig. 1.4.4, we have
and thus
It follows that the potential
that has H
of (6) as the negative of its gradient is
Note that the potential is multiple valued as the origin is encircled more than once. This property reflects the fact that strictly, H is not curl free in all of space. As the origin is encircled, Ampère's integral law identifies J as the source of the curl of H.
Because
is a solution to Laplace's equation, it must possess an EQS analog. The electroquasistatic potential
describes the fringing field of a capacitor of semi-infinite extent, extending from x = 0 to x = +
, with a voltage V across the plates, in the limit as the spacing between the plates is negligible (Fig. 5.7.2 with V reversed in sign). It can also be interpreted as the field of a semi-infinite dipole layer with the dipole density
s =
s d =
o V defined by (4.5.27), where d is the spacing between the surface charge densities,

s, on the outside surfaces of the semi-infinite plates (Fig. 5.7.2 with the signs of the charges reversed). We now have further opportunity to relate H fields of current-carrying wires to EQS analogs involving dipole layers.
The Scalar Potential of a Current Loop
A current loop carrying a current i has a magnetic
field that is curl free everywhere except at the location of the
wire. We shall now determine the scalar potential produced by the
current loop. The line integral 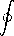 H
H  ds enclosing the current does not give zero, and hence
paths that enclose the current in the loop are not allowed, if the
potential is to be single valued. Suppose that we
mount over the loop a surface S spanning the loop which is not
crossed by any path of integration. The actual shape of the surface
is arbitrary, but the contour Cl is defined by the wire which is
its edge. The potential is then made single valued. The
discontinuity of potential across the surface follows from
Ampère's law
ds enclosing the current does not give zero, and hence
paths that enclose the current in the loop are not allowed, if the
potential is to be single valued. Suppose that we
mount over the loop a surface S spanning the loop which is not
crossed by any path of integration. The actual shape of the surface
is arbitrary, but the contour Cl is defined by the wire which is
its edge. The potential is then made single valued. The
discontinuity of potential across the surface follows from
Ampère's law

where the broken circle on the integral sign is to indicate a path as
shown in Fig. 8.3.1 that goes from one side of the surface to a point
on the opposite side. Thus, the potential  of a current loop
has the discontinuity
of a current loop
has the discontinuity

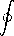 H
H  ds.
ds.
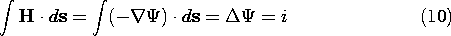
We have found in electroquasistatics that a uniform dipole layer of
magnitude  s on a surface S produces a potential that
experiences a constant potential jump
s on a surface S produces a potential that
experiences a constant potential jump  s/
s/ o across the surface,
(4.5.31). Its potential was (4.5.30)
o across the surface,
(4.5.31). Its potential was (4.5.30)

where 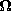 is the solid angle subtended by the rim of the surface
as seen by an observer at the point r. Thus, we conclude that
the scalar potential
is the solid angle subtended by the rim of the surface
as seen by an observer at the point r. Thus, we conclude that
the scalar potential  , a solution to Laplace's equation with a
constant jump i across the surface S spanning the wire loop, must
have a potential jump
, a solution to Laplace's equation with a
constant jump i across the surface S spanning the wire loop, must
have a potential jump  s/
s/ o
o 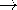 i, and hence the
solution
i, and hence the
solution

where again the solid angle is that subtended by the contour along
the wire as seen by an observer at the point r as shown by Fig.
8.3.2. In the example of a dipole layer, the surface S specified
the physical distribution of the dipole layer. In the present case,
S is arbitrary as long as it spans the contour C of the wire.
This is consistent with the fact that the solid angle 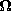 is
invariant with respect to changes of the surface S and depends only
on the geometry of the rim.
is
invariant with respect to changes of the surface S and depends only
on the geometry of the rim.
Example 8.3.2. The H Field of Small Loop
Consider a small loop of area a at the origin of a spherical coordinate system with the normal to the surface parallel to the z axis. According to (12), the scalar potential of the loop is then
This is the potential of a dipole. The H field follows from using (2)
As far as its field around and far from the loop is concerned, the current loop can be viewed as if it were a "magnetic" dipole, consisting of two equal and opposite magnetic charges
qm spaced a distance d apart (Fig. 4.4.1 with q
qm). The magnetic charges (monopoles) are sources of divergence of the magnetic flux
oH analogous to electric charges as sources of divergence of the displacement flux density
oE. Thus, if Maxwell's equations are modified to include the action of a magnetic charge density
in units of voltsec/m4, then the new magnetic Gauss' law must be
in analogy with
Now, magnetic monopoles have been postulated by Dirac, and recent searches for the existence of such monopoles have been apparently successful
2 Science Vol. 216, (June 4, 1982).
. Because the search is so difficult, it is apparent that, if they exist at all, they are very rare in nature. Here the introduction of magnetic charge is a matter of convenience so that the field produced by a small current loop can be pictured as the field of a magnetic dipole. This can serve as a mnemonic for the reconstruction of the field. Thus, if it is remembered that the potential of the electric dipole is
the potential of a magnetic dipole can be easily recalled as
where
The magnetic dipole moment is defined as the product of the magnetic charge, qm, and the separation, d, or by
o times the current times the area of the current loop. Another symbol is used commonly for the "dipole moment" of a current loop, m
ia, the product of the current times the area of the loop without the factor
o. The reader must gather from the context whether the words dipole moment refer to pm or m = pm/
o. The magnetic field intensity H of a magnetic dipole at the origin, (14), is
Of course, the details of the field produced by the current loop and the magnetic charge-dipole differ in the near field. One has
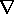

o H
0, and the other has a solenoidal H field.