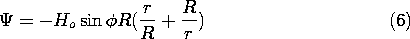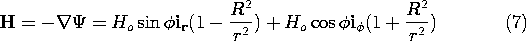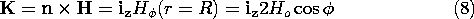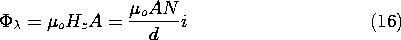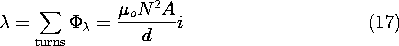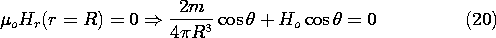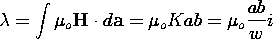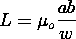8.4
Magnetoquasistatic Fields in the Presence of PerfectConductors

There are physical situations in which the current distribution is not prespecified but is given by some equivalent information. Thus, for example, a perfectly conducting body in a time-varying magnetic field supports surface currents that shield the H field from the interior of the body. The effect of the conductor on the magnetic field is reminiscent of the EQS situations of Sec. 4.6, where charges distributed themselves on the surface of a conductor in such a way as to shield the electric field out of the material.

We found in Chap. 7 that the EQS model of a perfect conductor described the low-frequency response of systems in the sinusoidal steady state, or the long-time response to a step function drive. We will find in Chap. 10 that the MQS model of a perfect conductor represents the high-frequency sinusoidal steady state response or the short-time response to a step drive.
Usually, we use the model of perfect conductivity to describe bodies of high but finite conductivity. The value of conductivity which justifies use of the perfect conductor model depends on the frequency (or time scale in the case of a transient) as well as the geometry and size, as will be seen in Chap. 10. When the material is cooled to the point where it becomes superconducting, a type I superconductor (for example lead) expels any mangetic field that might have originally been within its interior, while showing zero resistance to currrent flow. Thus, even for dc, the material acts on the magnetic field like a perfect conductor. However, type I materials also act to exclude the flux from the material, so they should be regarded as perfect conductors in which flux cannot be trapped. The newer "high temperature ceramic superconductors," such as Y₁Ba₂Cu₃O₇, show a type II regime. In this class of superconductors, there can be trapped flux if the material is cooled in a dc field. "High temperature superconductors" are those that show a zero resistance at temperatures above that of liquid nitrogen, 77 degrees Kelvin.

As for EQS systems, Faraday's continuity condition, (1.6.12), requires that the tangential E be continuous at a boundary between free space and a conductor. By definition, a stationary perfect conductor cannot have an electric field in its interior. Thus, in MQS as well as EQS systems, there can be no tangential E at the surface of a perfect conductor. But the primary laws determining H in the free space region, Ampère's law with J = 0 and the flux continuity condition, do not involve the electric field. Rather, they involve the magnetic field, or perhaps the vector or scalar potential. Thus, it is desirable to also state the boundary condition in terms of H or .

Boundary Conditions and Evaluation of Induced Surface Current Density
To identify the boundary condition on the magnetic field at the surface of a perfect conductor, observe first that the magnetic flux continuity condition requires that if there is a time-varying flux density n 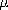_o H normal to the surface on the free space side, then there must be the same flux density on the conductor side. But this means that there is then a time-varying flux density in the volume of the perfect conductor. Faraday's law, in turn, requires that there be a curl of E in the conductor. For this to be true, E must be finite there, a contradiction of our definition of the perfect conductor. We conclude that there can be no normal component of a time-varying magnetic flux density at a perfectly conducting surface.

Correspondingly, if the H field is the gradient of the scalar potential , we find that

on the surface of a perfect conductor. This should be contrasted with the boundary condition for an EQS potential 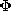which must be constant on the surface of a perfect conductor. This boundary condition can be used to determine the magnetic field distribution in the neighborhood of a perfect conductor. Once this has been done, Ampère's continuity condition, (1.4.16), can be used to find the surface current density that has been induced by the time-varying magnetic field. With n directed from the perfect conductor into the region of free space,

Because there is no time-varying magnetic field in the conductor, only the tangential field intensity on the free space side of the surface is required in this evaluation of the surface current density.

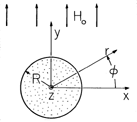
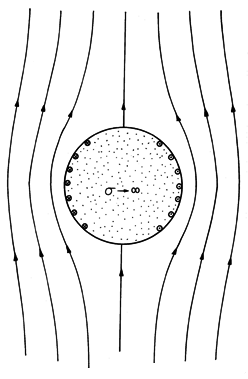
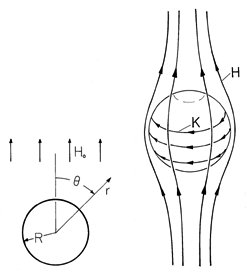
Example 8.4.1. Perfectly Conducting Cylinder in a Uniform Magnetic Field

A perfectly conducting cylinder having radius R and extending to z = is immersed in a uniform time-varying magnetic field. This field is y directed and has intensity H_o at infinity, as shown in Fig. 8.4.1. What is the distribution of H in the neighborhood of the cylinder?

Figure 8.4.1 Perfectly conducting circular cylinder of radius R in a magnetic field that is y directed and of magnitude H_o far from the cylinder.

In the free space region around the cylinder, there is no current density. Thus, the field can be written as the gradient of a scalar potential (in two dimensions)

The far field has the potential

The condition / n = 0 on the surface of the cylinder suggests that the boundary condition at r = R can be satisfied by adding to (5) a dipole solution proportional to sin /r. By inspection,

has the property / r = 0 at r = R. The magnetic field follows from (6) by taking its negative gradient

The current density induced on the surface of the cylinder, and responsible for generating the magnetic field that excludes the field from the interior of the cylinder, is found by evaluating (3) at r = R.

The field intensity of (7) and this surface current density are shown in Fig. 8.4.2. Note that the polarity of K is such that it gives rise to a magnetic dipole field that tends to buck out the imposed field. Comparison of (7) and the field of a two-dimensional dipole, (8.1.21), shows that the induced moment is id = 2 H_o R².

Figure 8.4.2 Lines of magnetic field intensity for perfectly conducting cylinder in transverse magnetic field.
There is an analogy to steady conduction (H J) in the neighborhood of an insulating rod immersed in a conductor carrying a uniform current density. In Demonstration 7.5.2, an electric dipole field also bucked out an imposed uniform field (J) in such a way that there was no normal field on the surface of a cylinder.

Voltage at the Terminals of a Perfectly Conducting Coil

Faraday's law was the underlying reason for the vanishing of the flux density normal to a perfect conductor. By stating this boundary condition in terms of the magnetic field alone, we have been able to formulate the magnetic field of perfect conductors without explicitly solving for the distribution of electric field intensity. It would seem that for the determination of the voltage induced by a time-varying magnetic field at the terminals of the coil, knowledge of the E field would be necessary. In fact, as we now take care to define the circumstances required to make the terminal voltage of a coil a well-defined variable, we shall see that we can put off the detailed determination of E for Chap. 10.

The EMF at point (a) relative to that at point (b) was defined in Sec. 1.6 as the line integral of E ds from (a) to (b). In Sec. 4.1, where the electric field was irrotational, this integral was then defined as the voltage at point (a) relative to (b). We shall continue to use this terminology, which is consistent with that used in circuit theory.
If the voltage is to be a well-defined quantity, independent of the layout of the connecting wires, the terminals of the coil shown in Fig. 8.4.3 must be in a region where the magnetic induction is negligible compared to that in other regions and where, as a result, the electric field is irrotational. To determine the voltage, the integral form of Faraday's law, (1.6.1), is applied to the closed line integral C shown in Fig. 8.4.3.

Figure 8.4.3 A coil having terminals at (a) and (b) links flux through surface enclosed by a contour composed of C₁ adjacent to the perfectly conducting material and C₂ completing the circuit between the terminals. The direction of positive flux is that of da, defined with respect to ds by the right-hand rule (Fig. 1.4.1). For the effect of magnetic induction to be negligible in the neighborhood of the terminals, the coil should have many turns, as shown by the inset.
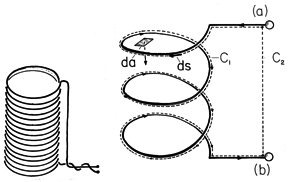
The contour goes from the terminal at (a) to that at (b) along the coil wire and closes through a path outside the coil. However, we know that E is zero along the perfectly conducting wire. Hence, the entire contribution to the line integral comes from the short path between the terminals. Thus, the left side of (9) reduces to

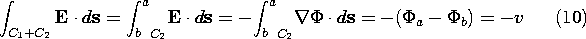
It follows from Faraday's law, (9), that the terminal voltage is

where 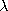is the flux linkage

³ We drop the subscript f on the symbol for flux linkage where there is no chance to mistake it for line charge density.

By definition, the surface S spans the closed contour C. Thus, as shown in Fig. 8.4.3, it has as its edge the perfectly conducting coil, C₁, and the contour used to close the circuit in the region where the terminals are located, C₂. If the magnetic induction is negligible in the latter region, the electric field is irrotational. In that case, the specific contour, C₂, is arbitrary, and the EMF between the terminals becomes the voltage of circuit theory.
Our discussion has emphasized the importance of having the terminals in a region where the magnetic induction, _o H/ t, is negligible. If a time-varying magnetic field is significant in this region, then different arrangements of the leads connecting the terminals to the voltmeter will result in different voltmeter readings. (We will emphasize this point in Sec. 10.1, where we develop an appreciation for the electric field implied by Faraday's law throughout the free space region surrounding the perfect conductors.) However, there remains the task of identifying configurations in which the flux linkage is not appreciably affected by the layout of leads connected to the terminals. In the absence of magnetizable materials, this is generally realized by making coils with many turns that are connected to the outside world through leads arranged to link a minimum of flux. The inset to Fig. 8.4.3 shows an example. The large number of turns assures a magnetic field within the coil that is much larger than that associated with the wires that connect the coil to the terminals. By intertwining these wires, or at least having them close together, the terminal voltage becomes independent of the detailed wire layout.

Demonstration 8.4.1. Surface used to Define the Flux Linkage
The surface S used to define in (12) is often geometrically complex. It is helpful to picture the surface in terms of a model. Shown in Fig. 8.4.4 is a three-turn coil. The surface is filled in by stringing yarn between a vertical rod joining the terminals in the external region and points on the wire. The surface is filled in by connecting points of decreasing altitude on the rod to points of increasing distance along the wire. Note from Fig. 8.4.3 that da and ds are related by the right-hand rule, where the latter is directed along the contour from the positive terminal to the negative one.

Figure 8.4.4 To visualize the surface enclosed by the contour C₁ + C₂ of Fig. 8.4.3, imagine filling it in with yarn strung on a frame representing the contour.
Another way of demonstrating the relationship of the surface to the coil geometry takes advantage of the phenomenon familiar from blowing bubbles. A small coil, closed along the external segment between the terminals, can be dipped into materials like soap solution to form a continuous film having the wire as one continuous edge. In fact, if the film is formed from a material that hardens into a plastic sheet, a permanent model for the surface is obtained.

Inductance

When the flux linked by the perfectly conducting coil of Fig. 8.4.3 is due entirely to a current i in the coil itself, is proportional to i, = Li. Thus, the inductance L, defined as

becomes a parameter that is only a function of geometric variables and _o. In this case, the terminal voltage given by (11) assumes a form familiar from circuit theory.

The following example illustrates this rule.

Example 8.4.2. Inductance of a Long Solenoid

In Demonstration 8.2.1, we examined the field of a long N-turn solenoid and found that in the limit where the length d becomes very large, the field intensity along the axis is

where i is the current in each turn.

For an infinitely long solenoid this is not only the field on the axis of symmetry but everywhere inside the solenoid. To see this, observe that a uniform magnetic field intensity satisfies both Ampère's law and the flux continuity condition throughout the free space interior region. (A uniform field is irrotational and solenoidal.) Further, with the field given by (15) inside the coil and taken as zero outside, Ampère's continuity condition (1.4.16) is satisfied at the surface of the coil where K = Ni/d. The normal flux continuity condition is automatically satisfied, since there is no flux density normal to the coil surface.

Because the field is uniform over the circular cylindrical cross-section, the magnetic flux

⁴ We use the symbol for the flux through one turn of a coil or a loop. passing through one turn of the solenoid is simply the cross-sectional area A of the solenoid multiplied by the flux density _o H.

The flux linkage, defined by (12), is obtained by summing the contributions of all the turns.

Thus, from (13),

For the circular cylindrical solenoid of radius a, A = a². The same arguments used to see that the interior field of a solenoid of circular cross-section is given by (15) show that the solenoid can have an arbitrary cross-sectional geometry and the field will still be given by (15) everywhere inside and be zero outside. Thus, (18) is applicable to a solenoid of arbitrary cross-section.

Example 8.4.3. Dipole Moment Induced in Perfectly Conducting Sphere by Imposed Uniform Magnetic Field

If a highly conducting material is immersed in a magnetic field, it will modify the field in its vicinity via a surface current that cancels the field in its interior. If the material is spherical, we can superimpose the field of a dipole and the uniform field to exactly satisfy the boundary condition on the conducting surface. For a sphere having radius R in an imposed field H_o i_z, as shown in Fig. 8.4.5, what is the equivalent dipole moment m?

Figure 8.4.5 Immersed in a uniform magnetic field, a perfectly conducting sphere has the same effect as an oppositely directed magnetic dipole.
The imposed field is conveniently analyzed into radial and azimuthal components. Then the irrotational and solenoidal field proposed to satisfy the boundary conditions is the sum of that uniform field and the field of a dipole at the origin, as given by (8.3.14) together with the definition (8.3.19).

By design, this field already approaches the uniform field at infinity. To satisfy the condition that n _o H = 0 at r = R,

It follows that the equivalent dipole moment is

The surface currents induced in the sphere which buck out the imposed magnetic flux are responsible for the dipole moment, as illustrated in Fig. 8.4.5.

Example 8.4.4. One-Turn "Solenoid"

The structure of perfectly conducting sheets shown in Fig. 8.4.6 has width w much greater than a and is excited by a uniform (in the z direction) current per unit length K at y = -b.
The H-field solution that satisfies the boundary condition n H = 0 and n x H = K on the perfect conductor is

Figure 8.4.6 One-turn solenoid.
What is the voltage that appears across the current generator? From (11) and (12) we conclude

with

where i is the total current supplied by the generator. The voltage is thus

where