9.2
Laws and Continuity Conditions with Magnetization

Recall that the effect of a spatial distribution of electric dipoles upon the electric field is described by a generalization of Gauss' law for electric fields, (6.2.1) and (6.2.2),

The effect of the spatial distribution of magnetic dipoles upon the magnetic field intensity is now similarly taken into account by generalizing the magnetic flux continuity law.

In this law, there is no analog to an unpaired electric charge density.

The continuity condition found by integrating (2) over an incremental volume enclosing a section of an interface having a normal n is

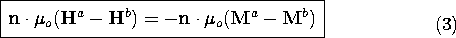
Suggested by the analogy to the description of polarization is the definition of the quantities on the right in (2) and (3), respectively, as the magnetic 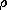charge density _m and the magnetic surface charge density _sm.

Faraday's Law Including Magnetization

The modification of the magnetic flux continuity law implies that another of Maxwell's equations must be generalized. In introducing the flux continuity law in Sec. 1.7, we observed that it was almost inherent in Faraday's law. Because the divergence of the curl is zero, the divergence of the free space form of Faraday's law reduces to

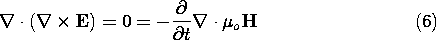
Thus, in free space, _o H must have a divergence that is at least constant in time. The magnetic flux continuity law adds the information that this constant is zero. In the presence of magnetizable material, (2) shows that the quantity _o(H + M ) is solenoidal. To make Faraday's law consistent with this requirement, the law is now written as

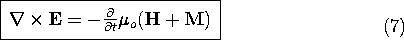
Magnetic Flux Density

The grouping of H and M in Faraday's law and the flux continuity law makes it natural to define a new variable, the magnetic flux density B.

This quantity plays a role that is analogous to that of the electric displacement flux density D defined by (6.2.14). Because there are no macroscopic quantities of monopoles of magnetic charge, its divergence is zero. That is, the flux continuity law, (2), becomes simply

and the corresponding continuity condition, (3), becomes simply

A similar simplification is obtained by writing Faraday's law in terms of the magnetic flux density. Equation (7) becomes

If the magnetization is specified independent of H, it is usually best to have it entered explicitly in the formulation by not introducing B. However, if M is given as a function of H, especially if it is linear in H, it is most convenient to remove M from the formulation by using B as a variable.

Terminal Voltage with Magnetization

In Sec. 8.4, where we discussed the terminal voltage of a perfectly conducting coil, there was no magnetization. The generalization of Faraday's law to include magnetization requires a generalization of the terminal relation.

The starting point in deriving the terminal relation was Faraday's integral law, (8.4.9). This law is generalized to included magnetization effects by replacing _o H with B. Otherwise, the derivation of the terminal relation, (8.4.11), is the same as before. Thus, the terminal voltage is again

but now the flux linkage is

In Sec. 9.4 we will see that Faraday's law of induction, as reflected in these last two relations, is the basis for measuring B.