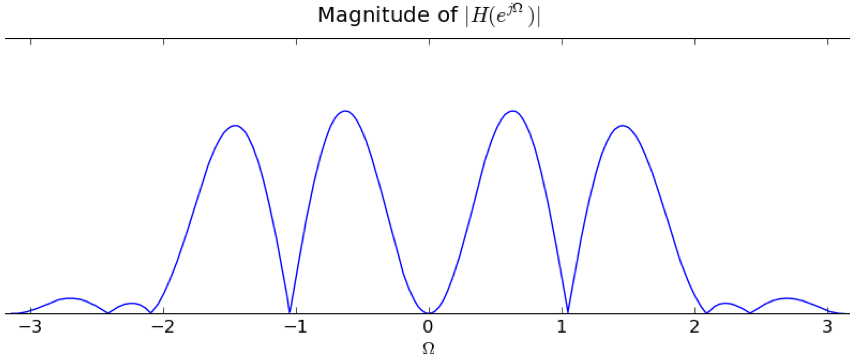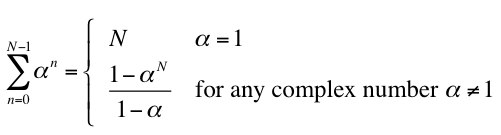
- expand the sum
- multiply expansion by (1–α)/(1–α)
- simplify the numerator


Problem .
Give an expression for the magnitude of a complex exponential with frequency φ, i.e., |ejφ|.
Problem .
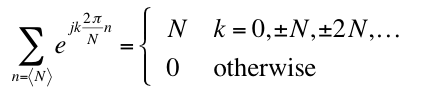
Problem .
Consider an LTI system characterized by the unit-sample response h[n].
Problem .
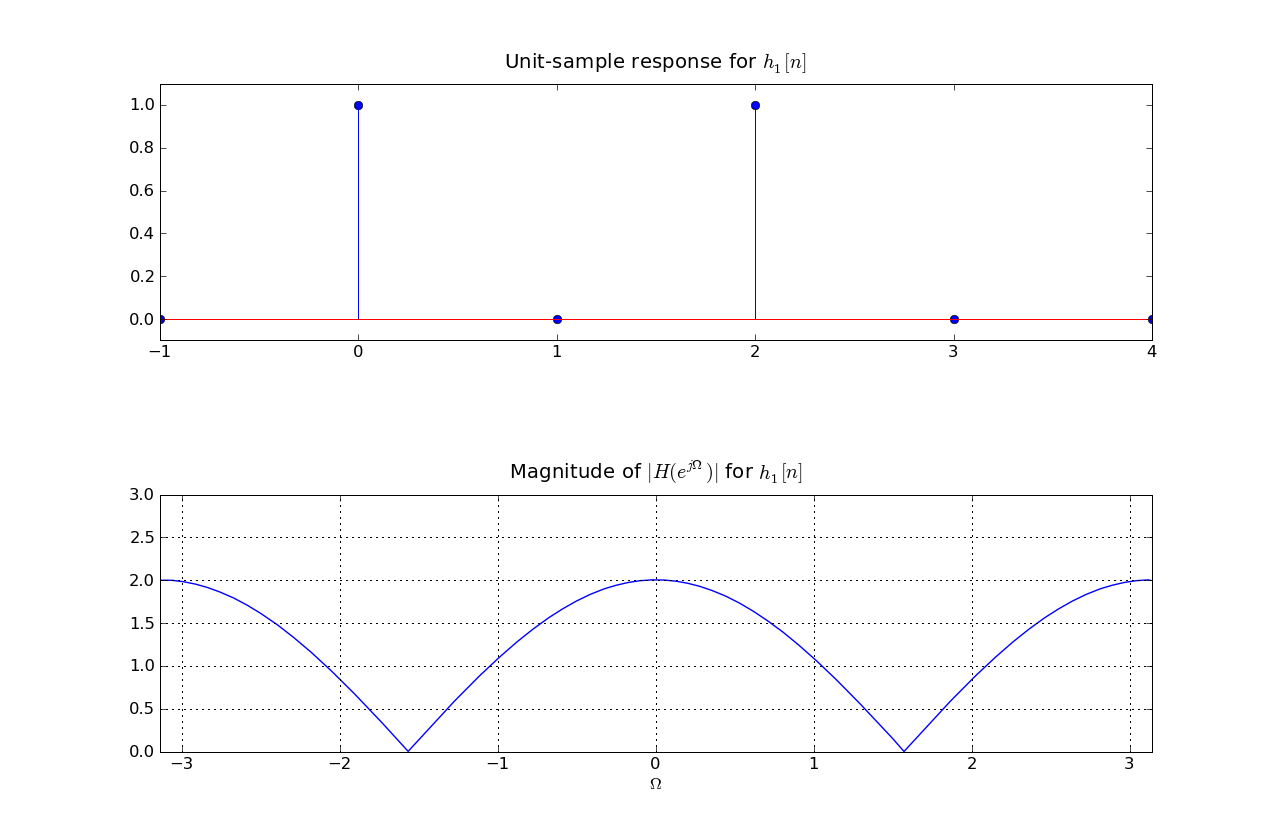
In answering the questions below, please consider the unit sample response and frequency response of two filters, H1 and H2, plotted below.
Note: the only nonzero values of unit sample response for H1 are : h1[0] = 1, h1[1]=0, h1[2]=1.
Note, the only nonzero values of unit sample response for H2 are : h2[0] = 1, h2[1]=-sqrt(3), h2[2]=1.
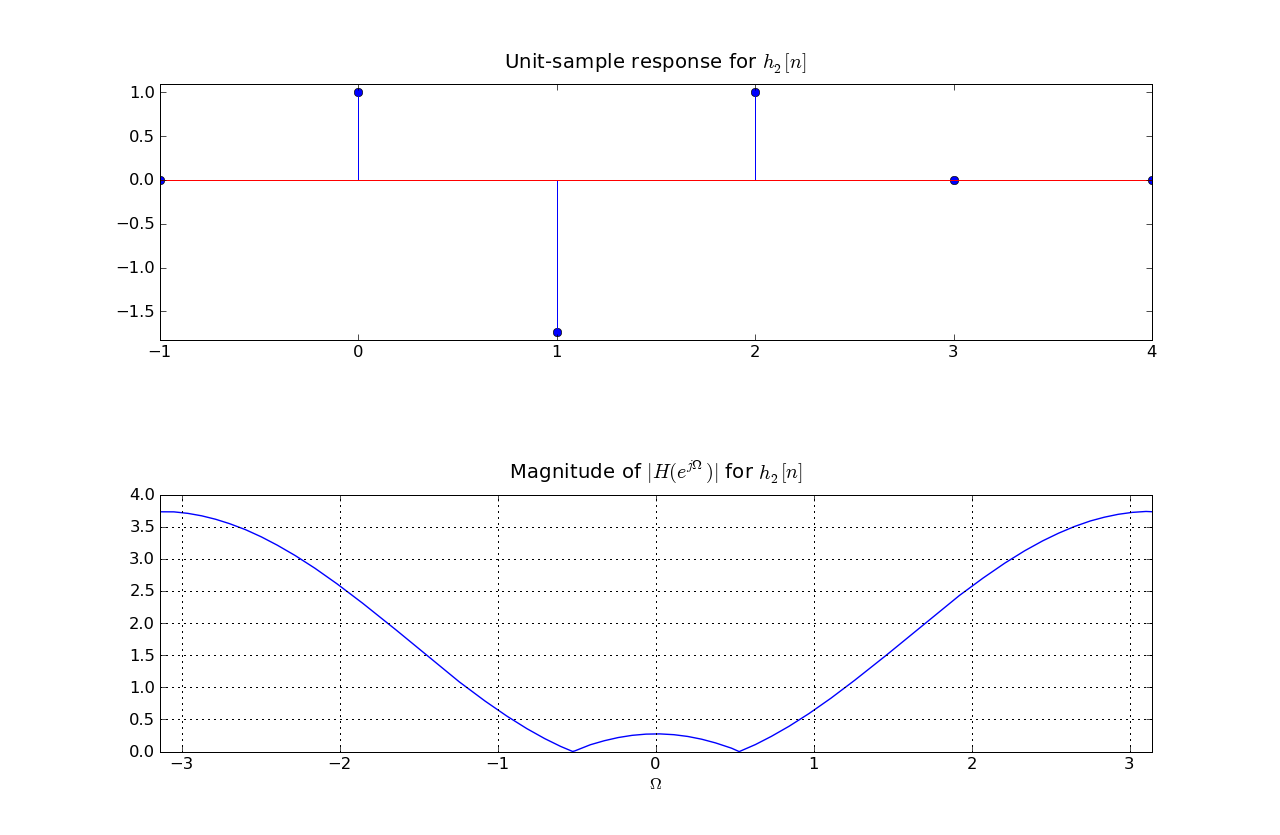
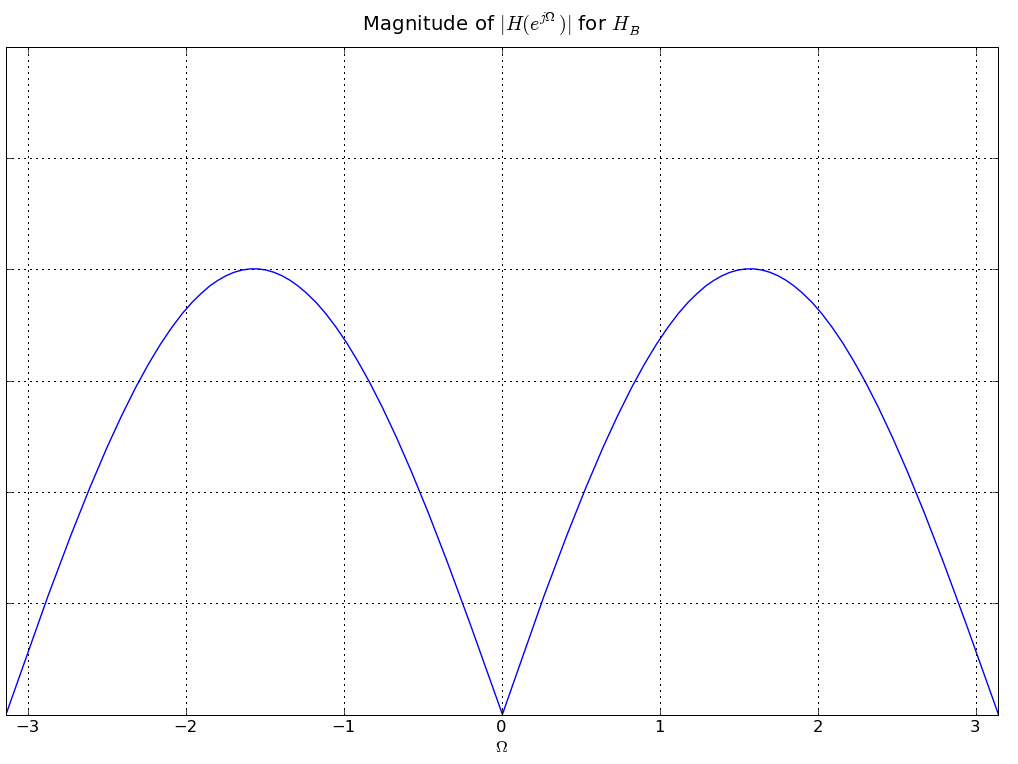
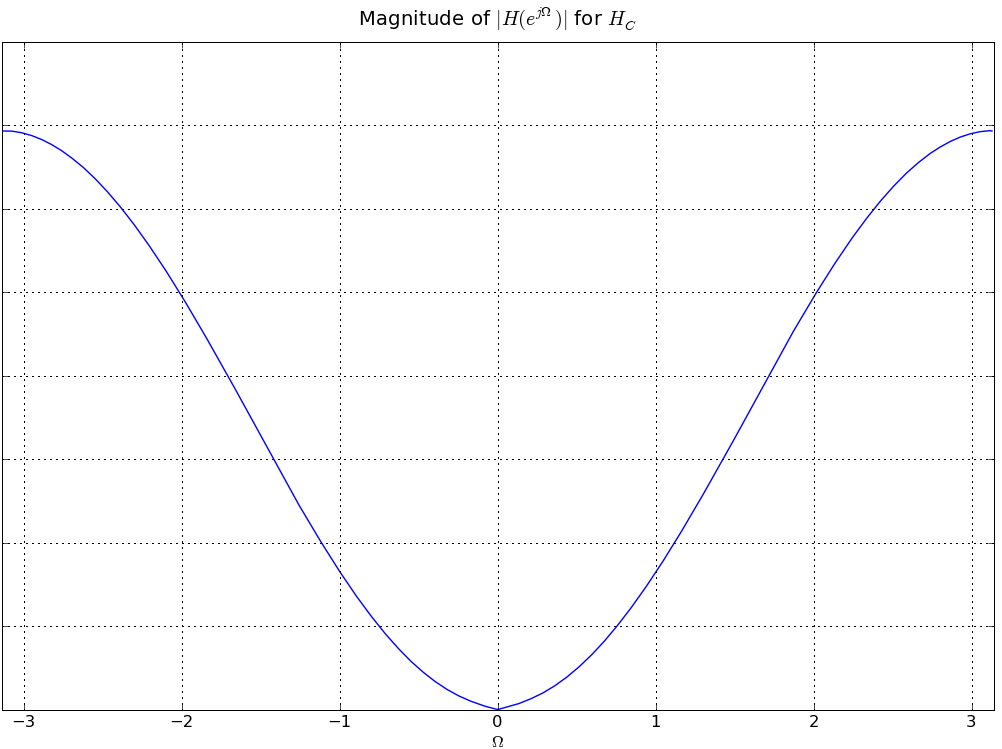
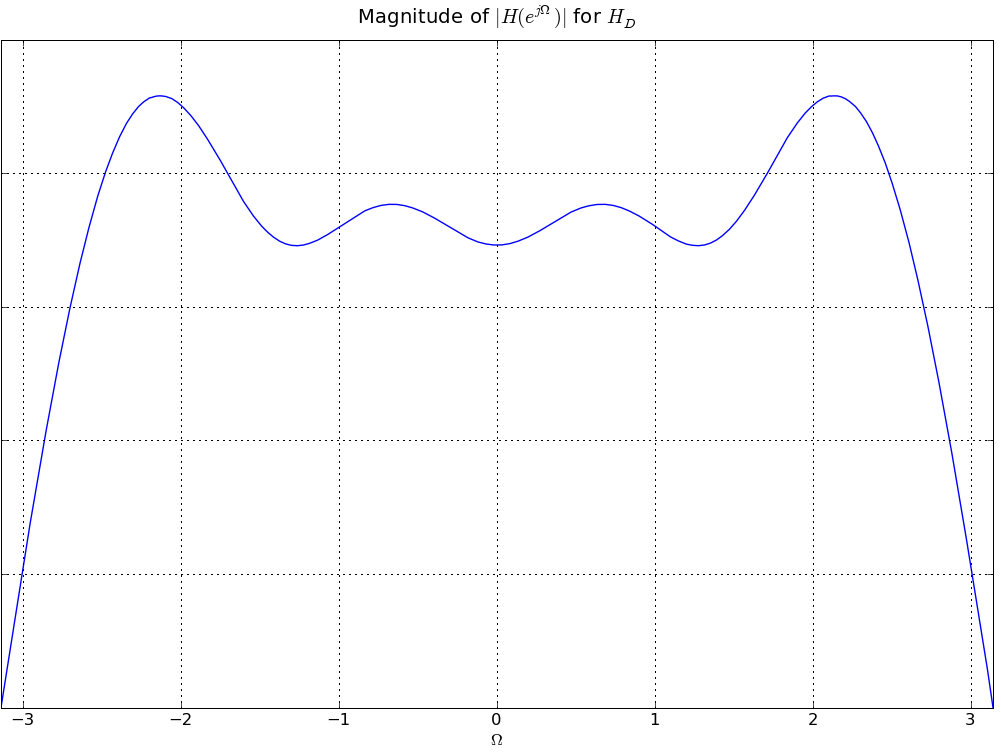
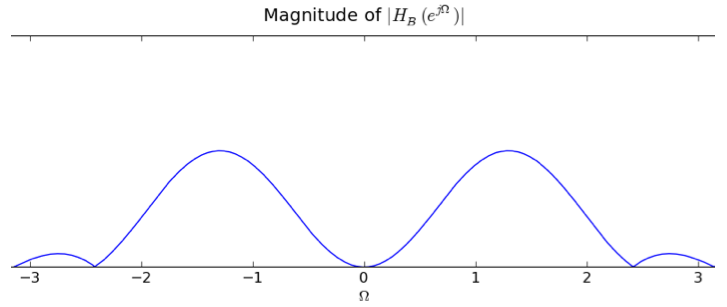
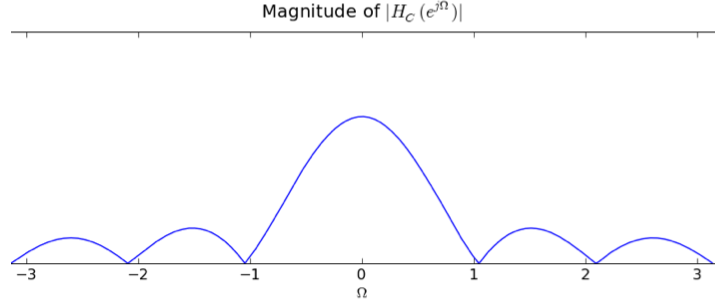
In answering the several parts of this review question consider four linear time-invariant systems, denoted A, B, C, and D, each characterized by the magnitude of its frequency response, |HA(ejΩ)|, |HB(ejΩ)|, |HC(ejΩ})|, and |HD(ejΩ)| respectively, as given in the plots below. This is a review problem, not an actual exam question, so similar concepts are tested multiple times to give you practice
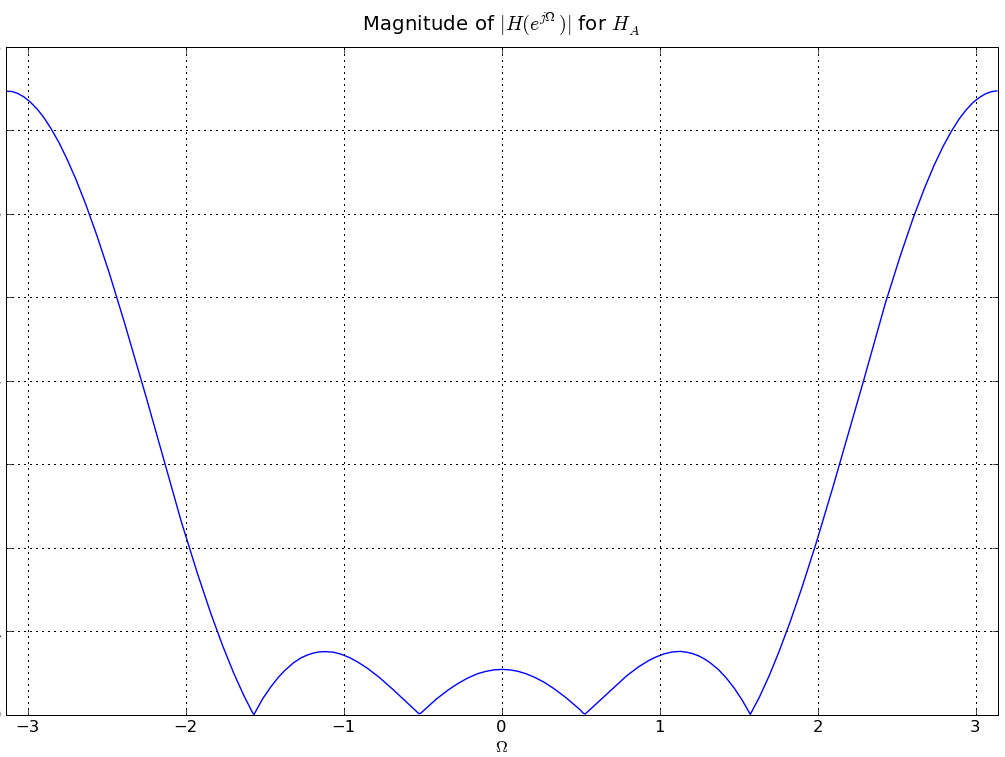
h[n] = α δ[n] - h1[n]
and what is the numerical value of |α|?
The frequency response is a linear operation. So to get the frequency response of the sum of two unit sample responses, we can simply add the frequency responses for the original ones. The frequency response for h1 is already given in the figure above and can be computed to give H(ejΩ) = 1 + e-2jΩ. (Problem 3 part b). The frequency response of
α δ[n] is simply the constant α . If we add the two responses and compute the magnitude of the result, we see that it must have exactly 2 extrema, one each at ± π/2. So it must be HB as that is the only frequency response that has extrema exactly at ± π/2
To determine α we look at the resulting response at the point where Omega is zero.
|α|=2 as H1(ej0)=2 but HB(ej0)=0.
h[n] = Σmh1[m]h2[n-m] for m = 0 to n
and what are the numerical values of h[2], h[3] and H(ej0)?
H(ej0) = H1(ej0)H2(ej0) = 2(2 - sqrt(3)) = 4 - 2sqrt(3)
h[n] = [1,0,1]*[1,-sqrt(3),1] so h[2] = 2 and h[3] = -sqrt(3).
h[n] = α δ[n] - Σmh1[m]h2[n-m] for m = 0 to n
and what is the numerical value of |α|?
HA is the frequency response for H1*H2 as seen in the previous question. The frequency response H here is H=α - HA using the same linearity argument as earlier. Hence H must have the same values at all those points where HA goes to zero. Since HA has 4 zeros, there are 4 such points where H must have the same values . In both HB and HD we can find 4 points that have the same value on the y-axis. But only in HD the x-coordinates of these 4 points match up to the x-coordinates of the zeroes of HA. So, HD must be the solution.
The resulting spectra in HD goes to zero at +/- PI. Since |HA(ejπ)| = |H1(ejπ)||H2(ejπ)|, |α| = 2(2 + sqrt(3)) = 4 + 2sqrt(3). This is similar to the way alpha was computed in part A.
h[n] = α δ[n] - h2[n]
and what is the numerical value of |α|?
HC(ej0) = 0 so |α| = |H2(ej0)| = 2 - sqrt(3).
x[n]=0 for n < 0 and
x[n] = cos(nπ/6) + cos(nπ/2) + 1.0 for n ≥ 0
Which system (A, B, C or D) produced an output, y[n] below, and what is the value of y[n] for n > 10?
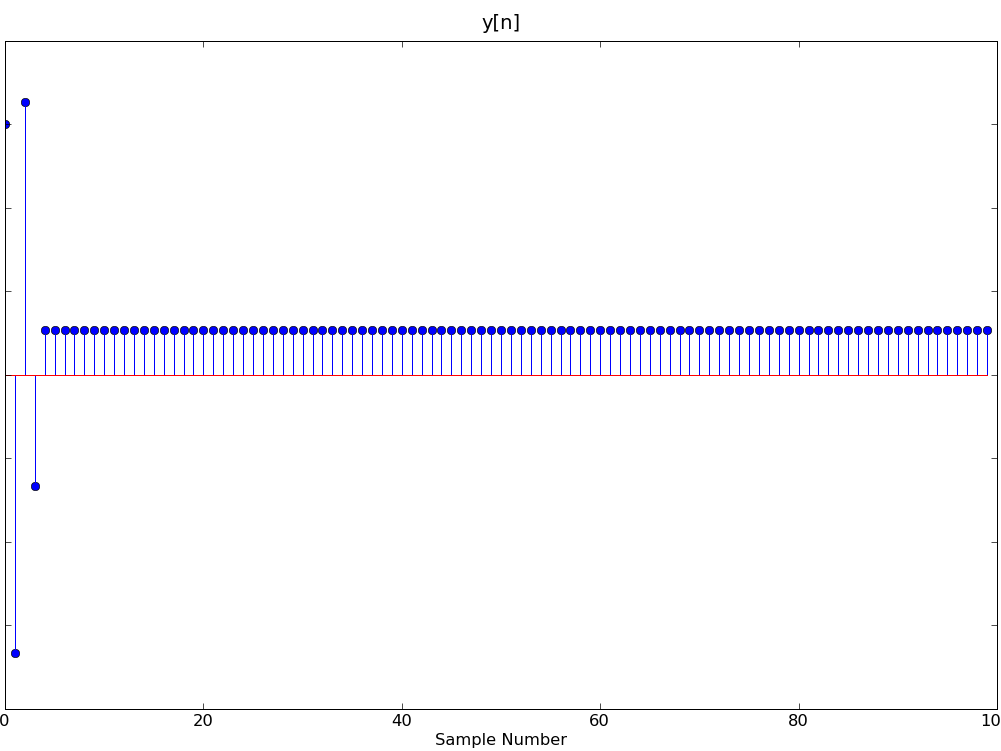
y[n] for n > 10 = |HA(ej0)|*1 = 4 - 2sqrt(3)
x[n]=0 for n < 0 and
x[n] = cos(nπ/6) + cos(nπ/2) + 1.0 for n ≥ 0
Which system (H1 or H2) produced an output, y[n] below, and what is the value of y[22]?
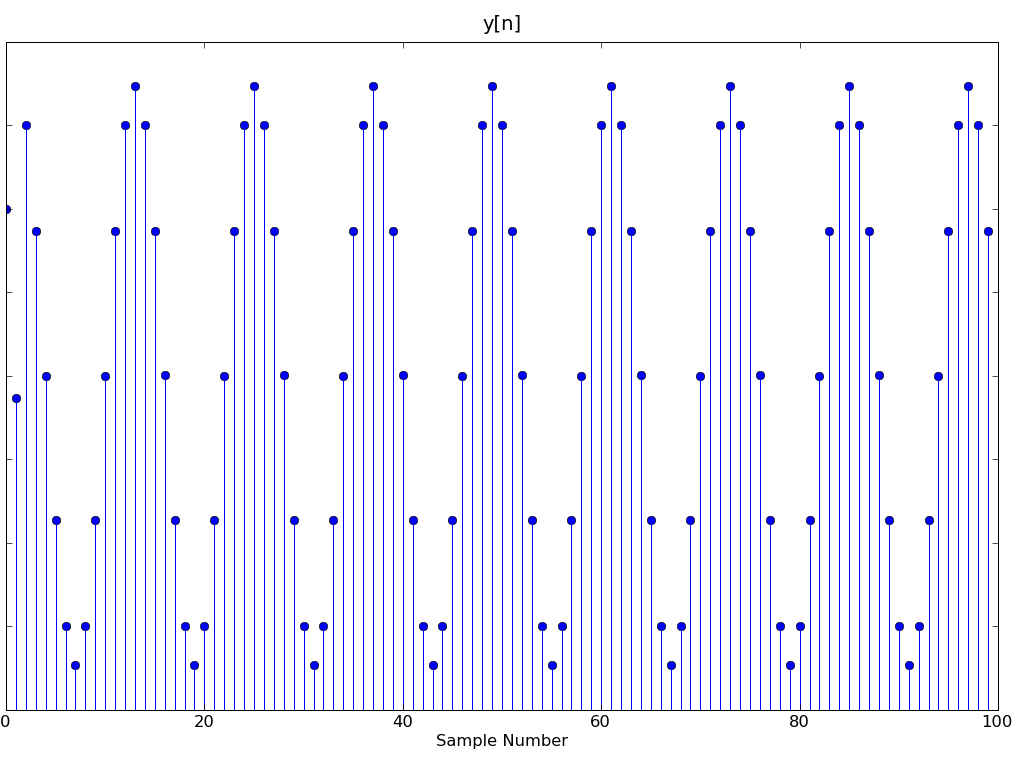
The resulting output signal has a period of 12 samples implying it's discrete frequency is PI/6. Hence it must be H1 since the H2 system would eliminate cos(π/6). This is because h2 is a 3-tap filter with nulling frequency at PI/6 (since h[2]=-2cos(Phi) and we know that h[2] is sqrt(3), Phi must be PI/6). Further more the resulting output signal doesn't have the PI/2 frequency component anymore. This is exactly what h1 eliminates if you look at it's frequency response. So, the system must be H1.
The output will eventually be a cosine added to H1(ej0)*1.
First compute some useful H's from the given h[n]:
H(ejΩ) = 1 + e-j2Ω H(ej0) = 1 + 1 = 2 H(ej(-π/6)) = 1 + ejπ/3 H(ej(π/6)) = 1 + e-jπ/3 H(ej(-π/2)) = 1 + ejπ = 1 - 1 = 0 H(ej(π/2)) = 1 + e-jπ = 1 - 1 = 0Now we can plug those into our equation for y[n] that uses the spectral coefficients for x[n] and the frequency response H:
y[n] = ΣkakH(ejk(2π/N))ejk(2π/N)n
= 2 + (1/2)H(ej(-π/6))ej(-π/6)n + (1/2)H(ej(π/6))ej(π/6)n
= 2 + (1/2)(1 + ejπ/3)ej(-π/6)n + (1/2)(1 + e-jπ/3)ej(π/6)n
= 2 + (1/2)ej(-π/6)n + (1/2)e-j((π/6)n - π/3) + (1/2)ej(π/6)n + (1/2)ej((π/6)n - π/3)
= 2 + cos((π/6)n) + cos((π/6)n - π/3)
So
y[22] = 2 + cos(22π/6) + cos(22π/6 - π/3)
= 2 + 0.5 - 0.5
= 2
Problem .
In answering the several parts of this question, consider three linear time-invariant filters, denoted A, B, and C, each characterized by the magnitude of their frequency responses, |HA(ejΩ)|, |HB(ejΩ)|, |HC(ejΩ)|, respectively, as given in the plots below.
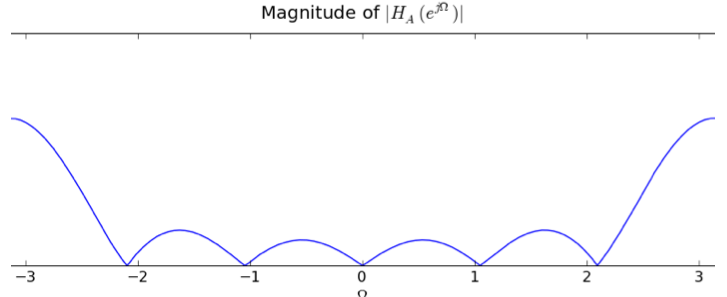
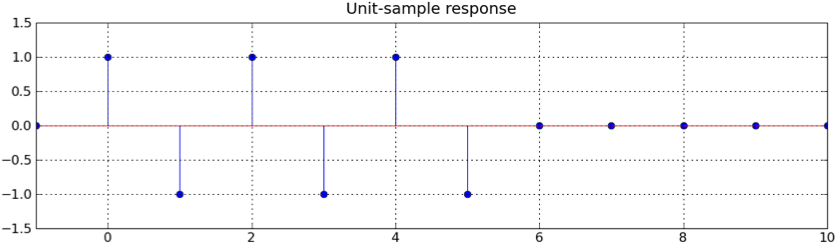
Ω=0: |H(ej0)| = |Σh[n](1)| = 0 Ω=π: |H(ejπ)| = |Σh[n](-1)n| = 6The only plot with a frequency response of 0 at frequency 0 and something non-zero at frequency π is the one for filter A.
Looking at the frequency response for A, it has its largest magnitude at ±π, which we calculated above to be 6.
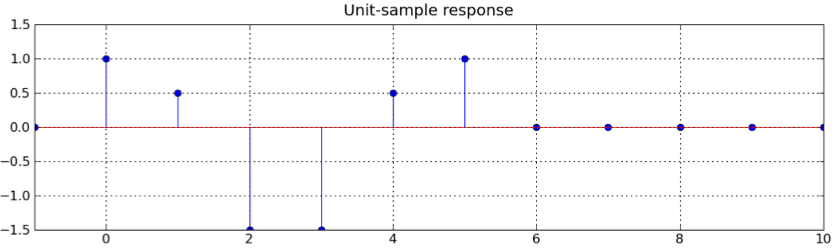
Ω=0: |H(ej0)| = |Σh[n]| = 1 + .5 - 1.5 - 1.5 + .5 + 1 = 0 Ω=π: |H(ejπ)| = |Σh[n](-1)n| = 1 -.5 - 1.5 + 1.5 +.5 - 1 = 0The only plot with a frequency response of 0 at frequencies 0 and π is the one for filter B.
The maximum magnitude of the frequency response is given by:
|H(ejΩ)| = |Σnh[n]e-jΩn| ≤ Σn|h[n]|(1) ≤ 6.So, no, it's not bigger than 6.
x[n] = cos((π/3)n) + cos(πn) + 1.0
Which filter (A, B,or C) produced the output, y[n] below, and what is maxΩ |H(ejΩ)| for your selected system?
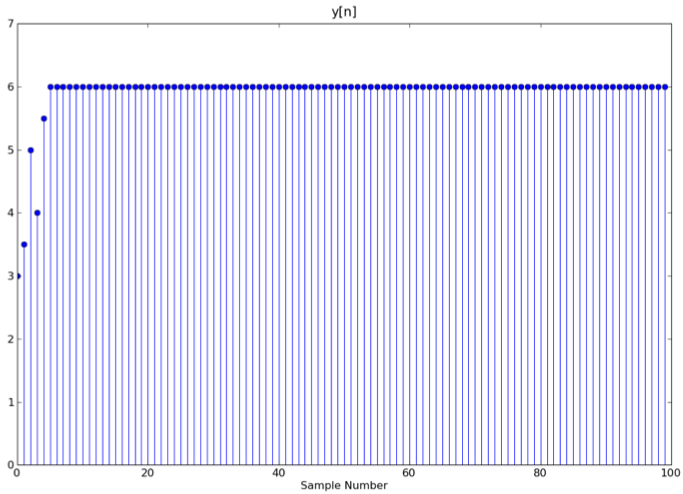
The only other component of x[n] is the constant 1, so that means that H(ej0) = 6 since constant inputs have frequency 0 and the constant output from the figure stays at 6.
The only plot that satisfies these conditions is C. From the plot of C's frequency response, the maximum magnitude occurs at frequency 0 and has the value 6 as we calculated above.
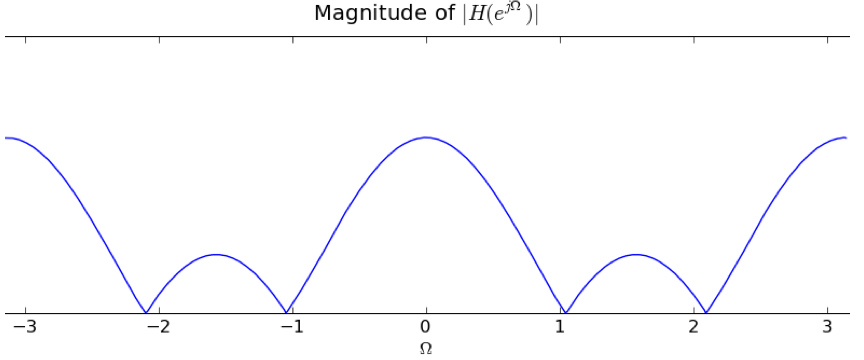
Which of the six new filters has the frequency response plotted below?
Which of the six new filters from the previous question has the frequency response plotted below?