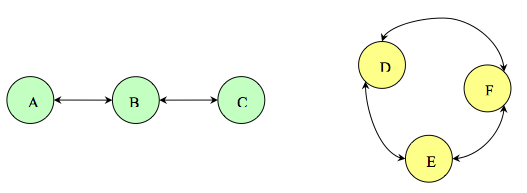


Problem . Consider the following networks: network I (containing nodes A, B, C) and network II (containing nodes D, E, F).

Please fill in the following table:
| Event | Number of time steps |
|---|---|
| A's routing table has an entry for B | |
| A's routing table has an entry for C | |
| D's routing table has an entry for E | |
| F's routing table has an entry for D |
| Event | Number of time steps |
|---|---|
| B's advertisements reflect that C is unreachable | |
| A's routing table reflects C is unreachable | |
| D's routing table reflects a new route for E |
MinCost: Every node picks the path that has the smallest sum of link costs along the path. (This is the minimum cost routing you implemented in the lab).
MinHop: Every node picks the path with the smallest number of hops (irrespective of what the cost on the links is).
SecondMinCost: Every node picks the path with the second lowest sum of link costs. That is, every node picks the second best path with respect to path costs.
MinCostSquared: Every node picks the path that has the smallest sum of squares of link costs along the path.
Assume that sufficient information (e.g., costs, delays, bandwidths, and loss probabilities of the various links) is exchanged in the link state advertisements, so that every node has complete information about the entire network and can correctly implement the strategies above. You can also assume that a link's properties don't change, e.g., it doesn't fail.
To see why SecondMinCost will not work: consider the triangle topology with 3 nodes A, B, D, and equal cost on all the links. The second route at A to D is via B, and the second best route at B to D is via A, resulting in a routing loop.
Problem . Which of the following tasks does a router R in a packet-switched network perform when it gets a packet with destination address D? Indicate True or False for each choice.
Problem . Alice and Bob are responsible for implementing Dijkstra's algorithm at the nodes in a network running a link-state protocol. On her nodes, Alice implements a minimum-cost algorithm. On his nodes, Bob implements a "shortest number of hops" algorithm. Give an example of a network topology with 4 or more nodes in which a routing loop occurs with Alice and Bob's implementations running simultaneously in the same network. Assume that there are no failures.
(Note: A routing loop occurs when a group of k ≥ 1 distinct nodes, n_0 , n_1 , n_2 , …, n_(k-1) have routes such that n_i's next-hop (route) to a destination is n_(i+1 mod k).
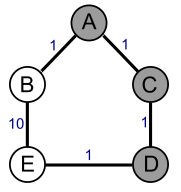
Suppose the destination is E. A will pick B as its next hop because ABE is the shortest path. B will pick A as its next hop because BACDE is the minimum-cost path (cost of 4, compared to 11 for the ABE path). The result is a routing loop ABABAB...
Problem . Consider the network shown below. The number near each link is its cost.
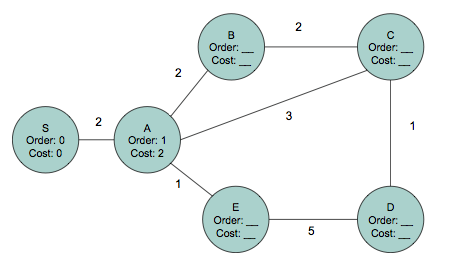
We're interested in finding the shortest paths (taking costs into account) from S to every other node in the network. What is the result of running Dijkstra's shortest path algorithm on this network? To answer this question, near each node, list a pair of numbers: The first element of the pair should be the order, or the iteration of the algorithm in which the node is picked. The second element of each pair should be the shortest path cost from S to that node.
To help you get started, we've labeled the first couple of nodes: S has a label (Order: 0, Cost: 0) and A has the label (Order: 1, Cost: 2).
Problem . Consider any two graphs(networks) G and G' that are identical except for the costs of the links. Please answer these questions.
Consider k=1 and h=1 and compute the costs and shortest paths in G'. Now the 3-hop path has cost 6 and the 1-hop path has cost 5. In G' the shortest path is the second path.
Problem . Dijkstra's algorithm
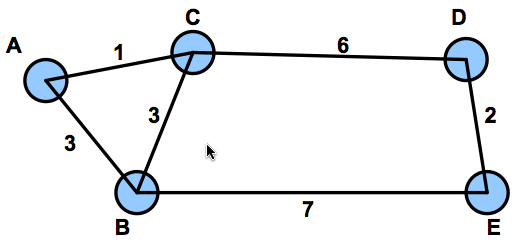
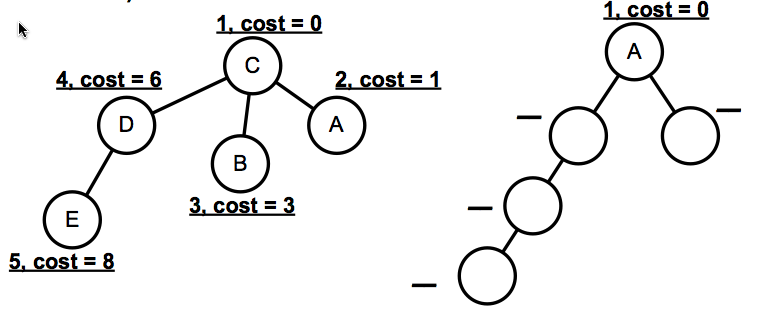
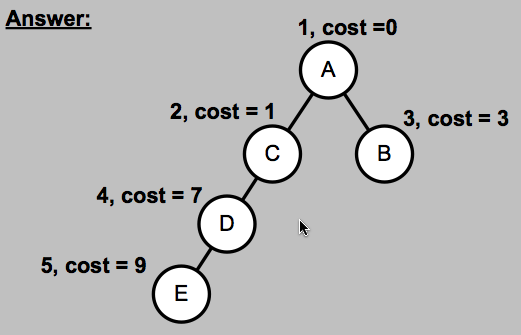
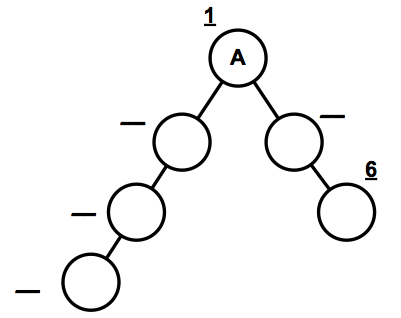
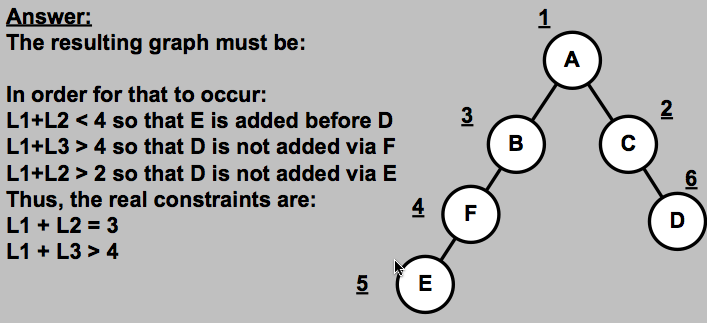
an empty routing tree generated by Dijkstra's algorithm for node A (to every other node) is shown below. Fill in the missing nodes and indicate the order that each node was added and its associated cost. For reference, node C's completed routing tree is shown as well.
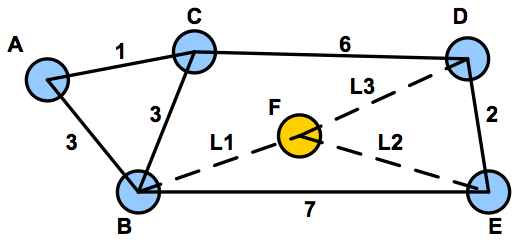
What are the constraints on L1, L2 and L3 such that node A's routing tree must match the topology shown below (regardless of how ties are broken in the algorithm), and it is known that node F is not the last node added when using Dijkstra's algorithm? All costs are positive integers.
First note that there are several possibilities for the tree, but only one really works as we will show.
Case 1: The left could be ACDF and the right could be ABE.
This case is impossible because ABE is not a min-cost path; ACDE has cost
9, which is less than the cost of ABE (10).
Case 2: The left is ACDE and the right is ABF.
This is not possible because F cannot be the last node added, and the last
node added is on the bottom right.
Case 3 is the only remaining possibility: The left is ABFE and the right
is ACD. We need to analyze this case to come up with the required constraints.
1) Node E is added before D, so cost(ABFE) < cost (ACD), so 3 + L1 + L2 < 1 + 6 ==> L1 + L2 < 4.
2) Node D is not added via F, so cost(ABFD) > cost(ACD), so 3 + L1 + L3 > 1 + 6 ==> L1 + L3 > 4
3) Node D is not added via E, so cost(ABFED) > cost(ACD), so 3 + L1 + L2 + 2 > 1 + 6 ==> L1 + L2 > 2.
Problem . Under some conditions, a distance vector protocol finding minimum cost paths suffers from the "count-to-infinity" problem. Indicate True or False for each choice.
Problem . Ben Bitdiddle has set up a multi-hop wireless network in which he would like to find paths with high probability of packet delivery between any two nodes. His network runs a distance vector protocol similar to what you developed in the pset. In Ben's distance vector (BDV) protocol, each node maintains a metric to every destination that it knows about in the network. The metric is the node’s estimate of the packet success probability along the path between the node and the destination.
The packet success proba bility along a link or path is defined as 1 minus the packet loss probability along the corresponding link or path. Each node uses the periodic HELLO messages sent by each of its neighbors to estimate the packet loss probability of the link from each neighbor. You may assume that the link loss probabilities are symmetric; i.e., the loss probability of the link from node A to node B is the same as from B to A. Each link L maintains its loss probability in the variable L.lossprob and 0 < L.lossprob < 1.
# Process an advertisement from a neighboring node in BDV
def integrate(self, fromnode, adv):
L = self.getlink(fromnode)
for (dest, metric) in adv:
my_metric = __________________________________
if (dest not in self.routes
or self.metric[dest] _____ my_metric
or ___________________________________________):
self.routes[dest] = L
self.metric[dest] = my_metric
# rest of integrate() not shown
Second blank: < (<= is also fine since we said that lossprob is strictly > 0)
Third blank: self.routes[dest] == L
Ben wants to try out a link-state protocol now. During the flooding step, each node sends out a link-state advertisement comprising its address, an incrementing sequence number, and a list of tuples of the form (neighbor,lossprob), where the lossprob is the estimated loss probability to the neighbor.
Ben would like to reuse, without modification, his implementation of Dijkstra's shortest paths algorithm from the pset, which takes a map in which the links have non-negative costs and produces a path that minimizes the sum of the costs of the links on the path to each destination.
Problem . We studied a few principles for designing networks in 6.02.
The abstraction provided by a circuit-switched network is that of a dedicated link of a fixed rate; a packet-switched network provides no such guarantee to the communicating end points.
Switches in a packet-switched network look-up the destination address of a packet during forwarding, but not in a circuit-switched network.
Problem . Eager B. Eaver implements distance vector routing in his network in which the links all have arbitrary positive costs. In addition, there are at least two paths between any two nodes in the network. One node, u, has an erroneous implementation of the integration step: it takes the advertised costs from each neighbor and picks the route corresponding to the minimum advertised cost to each destination as its route to that destination, without adding the link cost to the neighbor. It breaks any ties arbitrarily. All the other nodes are implemented correctly.
Let's use the term "correct route" to mean the route that corresponds to the minimum-cost path. Which of the following statements are true of Eager's network?
A is false because u could propagate an incorrect cost to its neighbors causing the neighbor to have an incorrect route. In fact, u's neighbors could do the same.
C is correct; a simple example is where the network is a tree, where there is exactly one path between any two nodes.
D is false; no routing loops can occur under the stated condition. We can reason by contradiction. Consider the shortest path from any node s to any other node t running the flawed routing protocol. If the path does not traverse u, no node on that path can have a loop because distance vector routing without any packet loss or failures is loop-free. Now consider the nodes for which the computed paths go through u; all these nodes are correctly implemented except for u, which means the paths between u and each of them is loop-free. Moreover, the path to u is itself loop-free because u picks one of its neighbors with smaller cost, and there is no possibility of a loop.
Problem . Consider a network running the link-state routing protocol as described in lecture and on the pset. How many copies of any given LSA are received by a given node in the network?
Problem . In implementing Dijkstra's algorithm in the link-state routing protocol at node u, Louis Reasoner first sets the route for each directly connected node v to be the link connecting u to v. Louis then implements the rest of the algorithm correctly, aiming to produce minimum-cost routes, but does not change the routes to the directly connected nodes. In this network, u has at least two directly connected nodes, and there is more than one path between any two nodes. Assume that all link costs are non-negative. Which of the following statements is true of u's routing table?
Problem . A network with N nodes and N bidirectional links is connected in a ring, and N is an even number.
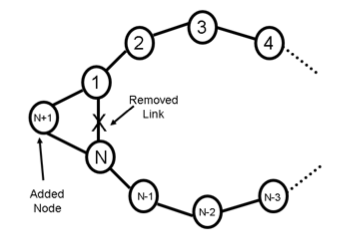
The network runs a distance-vector protocol in which the advertisement step at each node runs when the local time is T*i seconds and the integration step runs when the local time is T*i + T/2 seconds, (i=1,2,...). Each advertisement takes time δ to reach a neighbor. Each node has a separate clock and time is not synchronized between the different nodes.
Suppose that at some time t after the routing has converged, node N + 1 is inserted into the ring, as shown in the figure above. Assume that there are no other changes in the network topology and no packet losses. Also assume that nodes 1 and N update their routing tables at time t to include node N + 1, and then rely on their next scheduled advertisements to propagate this new information.
(N/2 - 1)*(T/2 + δ)
However, there is a small "fence-post error" in this argument. As stated in the problem, the nodes labeled 1 and N update their routing tables at time t to include node N + 1. In the best case, these two nodes could both immediately send out advertisements, and nodes 2 and N-1 could run their integration steps immediately after receiving these advertisements. Because of that, the delay of T/2 only starts applying to the other nodes in the network. Hence, the answer is
(N/2 - 2)*T/2 + (N/2 - 1)*δ
(N/2 -1)*(3T/2 + δ)
Problem . Louis Reasoner implements the link-state routing protocol discussed in 6.02 on a best-effort network with a non-zero packet loss rate. In an attempt to save bandwidth, instead of sending link-state advertisements periodically, each node sends an advertisement only if one of its links fails or when the cost of one of its links changes. The rest of the protocol remains unchanged. Will Louis' implementation always converge to produce correct routing tables on all the nodes?
Problem . Consider a network implementing minimum-cost routing using the distance-vector protocol. A node, S, has k neighbors, numbered 1 through k, with link cost c_i to neighbor i (all links have symmetric costs). Initially, S has no route for destination D. Then, S hears advertisements for D from each neighbor, with neighbor i advertising a cost of p_i. The node integrates these k advertisements. What is the cost for destination D in S's routing table after the integration?
mini{c_i + p_i}
Problem . Consider the network shown in the picture below. Each node implements Dijkstra's shortest path algorithm using the link costs shown in the picture.
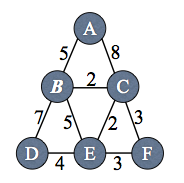
Problem . Alyssa P. Hacker implements the 6.02 distance-vector protocol on the network shown below. Each node has its own local clock, which may not be synchronized with any other node's clock. Each node sends its distance-vector advertisement every 100 seconds. When a node receives an advertisement, it immediately integrates it. The time to send a message on a link and to integrate advertisements is negligible. No advertisements are lost. There is no HELLO protocol in this network.

At time t = 10, D advertises to S, A, and C. They integrate this advertisement into their routing tables, so that cost(S,D) = 2, cost(A,D) = 2, cost(C,D) = 7. Note that only Sss route is correct. In the worst case, we wait 100s for the next round of advertisements. So at time t = 110, S, A, and C all advertise about D, and everyone integrates. Now cost(A, D) = 4 (via S), cost(B, D) = 4 (via S), and cost(C, D) = 7 still. A and B's routes are correct; C's is not. Finally, after 100 more seconds, another round of advertisements is sent. In particular, C hears about B's route to D, and updates cost(C, D) = 5 (via B).
Alyssa is unhappy that one of the links in the network carries a large amount of traffic when all the nodes are sending packets to D. She decides to overcome this limitation with Alyssa's Vector Protocol (AVP). In AVP, S lies, advertising a "path cost" for destination D that is different from the sum of the link costs along the path used to reach D. All the other nodes implement the standard distance-vector protocol, not AVP.