6.02 Quiz #3 Review Problems: Source Coding

Problem . Huffman and other coding schemes tend to devote more bits to the coding of

(A) symbols carrying the most information
(B) symbols carrying the least information
(C) symbols that are likely to be repeated consecutively
(D) symbols containing redundant information

Problem . Consider the following two Huffman decoding tress for a variable-length code involving 5 symbols: A, B, C, D and E.

1. Using Tree #1, decode the following encoded message: "01000111101". Starting at the root of the decoding tree, use the bits of the message to traverse the tree until a leaf node is reached; output that symbol. Repeat until all the bits in the message are consumed.

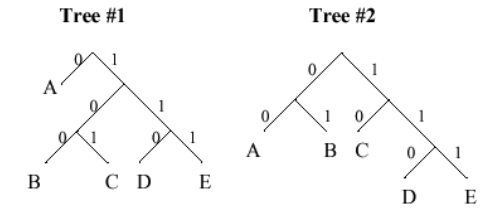
   0 = A
   100 = B
   0 = A
   111 = E
   101 = C
   

2. Suppose we were encoding messages with the following probabilities for each of the 5 symbols: p(A) = 0.5, p(B) = p(C) = p(D) = p(E) = 0.125. Which of the two encodings above (Tree #1 or Tree #2) would yield the shortest encoded messages averaged over many messages? Using Tree #1, the expected length of the encoding for one symbol is:

   1*p(A) + 3*p(B) + 3*p(C) + 3*p(D) + 3*p(E) = 2.0

   Using Tree #2, the expected length of the encoding for one symbol is:

   2*p(A) + 2*p(B) + 2*p(C) + 3*p(D) + 3*p(E) = 2.25

   So using the encoding represented by Tree #1 would yield shorter messages on the average.

3. Using the probabilities of part (B), if you learn that the first symbol in a message is "B", how many bits of information have you received? bits of info received = log2(1/p) = log2(1/.125) = 3

4. Using the probabilities of part (B), If Tree #2 is used to encode messages what is the average length of 100-symbol messages, averaged over many messages? In part (B) we calculated that the expected length of the encoding for one symbol using Tree #2 was 2.25 bits, so for 100-symbol messages the expected length is 225 bits.

Problem . Huffman coding is used to compactly encode the species of fish tagged by a game warden. If 50% of the fish are bass and the rest are evenly divided among 15 other species, how many bits would be used to encode the species when a bass is tagged? If a symbol has a probability of ≥ .5, it will be incorporated into the Huffman tree on the final step of the algorithm, and will become a child of the final root of the decoding tree. This means it will have a 1-bit encoding.

Problem . Ben Bitdiddle has been hired by the Registrar to help redesign the grades database for WebSIS. Ben is told that the database only needs to store one of five possible grades (A, B, C, D, F). A survey of the current WebSIS repository reveals the following probabilities for each grade:

Grade	Probability of occurrence
A	p(A) = 18%
B	p(B) = 27%
C	p(C) = 25%
D	p(D) = 15%
F	p(E) = 15%

1. Given the probabilities above, if you are told that a particular grade is "C", give an expression for the number of bits of information you have received. # of bits for "C" = log(1/pC) = log(1/.25) = log(4) = 2

2. Ben is interested in storing a sequence of grades using as few bits as possible. Help him out by creating a variable-length encoding that minimizes the average number of bits stored for a sequence of grades. Use the table above to determine how often a particular grade appears in the sequence. using Huffman algorithm:
   - since D,F are least probable, make a subtree of them, p(D/\F) = 30%
   - now A,C are least probable, make a subtree of them, P(A/\C) = 43%
   - now B,DF are least probable, make a subtree of them P(B/\(D/\F)) = 55%
   - just AC,BDF are left, make a subtree of them (A/\C)/\(B/\(D/\F))
   - so A = 00, B = 10, C = 01, D = 110, F = 111
   

Problem . Consider a sigma-delta modulator used to convert a particular analog waveform into a sequence of 2-bit values. Building a histogram from the 2-bit values we get the following information:

Modulator value	# of occurrences
00	25875
01	167836
10	167540
11	25974

1. Using probabilities computed from the histogram, construct a variable-length Huffman code for encoding these four values. p(00)=.0668 p(01)=.4334 p(10)=.4327 p(11)=.0671
   Huffman tree = 01 /\ (10 /\ (00 /\ 11))
   Code: 01="0" 10="10" 00="110" 11="111"

2. If we transmit the 2-bit values as is, it takes 2 bits to send each value (doh!). If we use the Huffman code from part (A) what is the average number of bits used to send a value? What compression ratio do we achieve by using the Huffman code? sum(pi*len(code for pi)) = 1.7005, which is 85% of the original 2- bit per symbol encoding.

3. Using Shannon's entropy formula, what is the average information content associated with each of the 2-bit values output by the modulator? How does this compare to the answers for part (B)? sum(pi*log2(1/pi)) = 1.568, so the code of part(B) isn't quite as efficient as we can achieve by using an encoding that codes multiple pairs as in one code symbol.

Problem . Several people at a party are trying to guess a 3-bit binary number. Alice is told that the number is odd; Bob is told that it is not a multiple of 3 (i.e., not 0, 3, or 6); Charlie is told that the number contains exactly two 1's; and Deb is given all three of these clues. How much information (in bits) did each player get about the number? N = 8 choices for a 3-bit number
Alice: odd = {001, 011, 101, 111} M=4, info = log2(8/4) = 1 bit
Bob: not a multiple of 3 = {001, 010, 100, 101, 111} M=5, info = log2(8/5) = .6781 bits
Charlie: two 1's = {011, 101, 110} M=3, info = log2(8/3) = 1.4150
Deb: odd, not a multiple of 3, two 1's = {101}, M=1, info = log(8/1) = 3 bits

Problem . In honor of Daisuke Matsuzaka's first game pitching for the Redsox, the Boston-based members of the Search for Extraterrestrial Intelligence (SETI) have decided to broadcast a 1,000,000 character message made up of the letters "R", "E", "D", "S", "O", "X". The characters are chosen at random according the probabilities given in the table below:

Letter	p(Letter)
R	.21
E	.31
D	.11
S	.16
O	.19
X	.02

1. If you learn that one of the randomly chosen letters is a vowel (i.e., "E" or "O") how many bits of information have you received? p(E or O) = .31 + .19 = .5, log2(1/pi) = 1 bit

2. Nervous about the electric bill for the transmitter at Arecibo, the organizers have asked you to design a variable length code that will minimize the number of bits needed to send the message of 1,000,000 randomly chosen characters. Please draw a Huffman decoding tree for your code, clearly labeling each leaf with the appropriate letter and each arc with either a "0" or a "1". Huffman algorithm:
   choose X,D: X/\D, p = .13
   choose S,XD: S/\(X/\D), p = .29
   choose R,0: R/\O, p = .40
   choose E,SXD: E/\(S/\(X/\D)), p = .6
   choose RO,ESXD: (R/\O) /\ (E/\(S/\(X/\D)))
   code: R=00 O=01 E=10 S=110 X=1110 D=1111
   

3. Using your code, what bit string would they send for "REDSOX"? 00 10 1111 110 01 1110

Problem . You're playing an on-line card game that uses a deck of 100 cards containing 3 Aces, 7 Kings, 25 Queens, 31 Jacks and 34 Tens. In each round of the game the cards are shuffled, you make a bet about what type of card will be drawn, then a single card is drawn and the winners are paid off. The drawn card is reinserted into the deck before the next round begins.

1. How much information do you receive when told that a Queen has been drawn during the current round? information received = log2(1/p(Queen)) = log2(1/.25) = 2 bits

2. Give a numeric expression for the average information content received when learning about the outcome of a round. (.03)log2(1/.03) + (.07)log2(1/.07) + (.25)log2(1/.25) + (.31)log2(1/.31) + (.34)log2(1/.34) = 1.97 bits

3. Construct a variable-length Huffman encoding that minimizes the length of messages that report the outcome of a sequence of rounds. The outcome of a single round is encoded as A (ace), K (king), Q (queen), J (jack) or X (ten). Specify your encoding for each of A, K, Q, J and X.

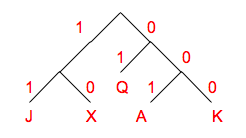
   Encoding for A: 001
   Encoding for K: 000
   Encoding for Q: 01
   Encoding for J: 11
   Encoding for X: 10
   

4. Using your code from part (C) what is the expected length of a message reporting the outcome of 1000 rounds (i.e., a message that contains 1000 symbols)? (.07+.03)(3 bits) + (.25+.31+.34)(2 bits) = 2.1 bits average symbol length using Huffman code. So expected length of 1000-symbol message is 2100 bits.

5. The Nevada Gaming Commission regularly receives messages in which the outcome for each round is encoded using the symbols A, K, Q, J and X. They discover that a large number of messages describing the outcome of 1000 rounds (i.e. messages with 1000 symbols) can be compressed by the LZW algorithm into files each containing 43 bytes in total. They immediately issue an indictment for running a crooked game. Briefly explain their reasoning. In order to achieve such a dramatic compression ratio, the original messages much have exhibited a very regular pattern - regular patterns would be very rare if the outcomes were truly random, hence the conclusion that the game was rigged. LZW should exhibit some improvement over Huffman since it will compactly encode pairs, triples, etc. But for messages of only 1000 symbols that process would not achieve an almost 10-to-1 improvement over Huffman.

Problem . X is an unknown 8-bit binary number. You are given another 8-bit binary number, Y, and told that the Hamming distance between X (the unknown number) and Y (the number you know) is one. How many bits of information about X have you been given? You've learned that X differs in exactly 1 of its 8 bits from the known number Y. So that means that knowing Y, we've narrowed down the value of X to one of 8 choices. Bits of information = log2(256/8) = 5 bits.

Problem . In Blackjack the dealer starts by dealing 2 cards each to himself and his opponent: one face down, one face up. After you look at your face-down card, you know a total of three cards. Assuming this was the first hand played from a new deck, how many bits of information do you now have about the dealer's face down card? We've narrowed down the choices for the dealer's face-down card from 52 (any card in the deck) to one of 49 cards (since we know it can't be one of three visible cards. bits of information = log2(52/49).

Problem . The following table shows the current undergraduate and MEng enrollments for the School of Engineering (SOE).

Course (Department)	# of students	Prob.
I (Civil & Env.)	121	.07
II (Mech. Eng.)	389	.23
III (Mat. Sci.)	127	.07
VI (EECS)	645	.38
X (Chem. Eng.)	237	.13
XVI (Aero & Astro)	198	.12
Total	1717	1.0

1. When you learn a randomly chosen SOE student's department you get some number of bits of information. For which student department do you get the least amount of information? We'll get the smallest value for log2(1/p) by choosing the choice with the largest p => EECS.

2. Design a variable length Huffman code that minimizes the average number of bits in messages encoding the departments of randomly chosen groups of students. Show your Huffman tree and give the code for each course. step 1 = {(I,.07) (II,.23) (III,.07) (VI,.38) (X,.13) (XVI,.12)}
   step 2 = {([I,III],.14) (II,.23) (VI,.38) (X,.13) (XVI,.12)}
   step 3 = {([I,III],.14) (II,.23) (VI,.38) ([X,XVI],.25)}
   step 4 = {([II,[I,III]],.37) (VI,.38) ([X,XVI],.25)}
   step 5 = {([[X,XVI],[II,[I,III]]]),.62) (VI,.38)}
   step 6 = {([[[X,XVI,[II,[I,III]],VI],1.0)}
   

   code for course I: 0 1 1 0
   code for course II: 0 1 0
   code for course III: 0 1 1 1
   code for course VI: 1
   code for course X: 0 0 0
   code for course XVI: 0 0 1
   

   There are of course many equivalent codes derived by swapping the "0" and "1" labels for the children of any interior node of the decoding tree. So any code that meets the following constraints would be fine:

   code for VI = length 1
   code for II, X, XVI = length 3
   code for I, III = length 4
   

3. If your code is used to send messages containing only the encodings of the departments for each student in groups of 100 randomly chosen students, what's the average length of such messages? Write an expression if you wish. 100*[(.38)(1) + (.23 + .13 + .12)*(3) + (.07 + .07)*(4)] = 238 bits