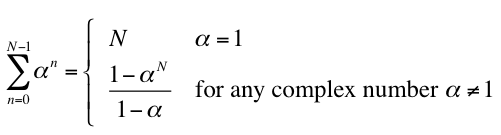
- expand the sum
- multiply expansion by (1–α)/(1–α)
- simplify the numerator
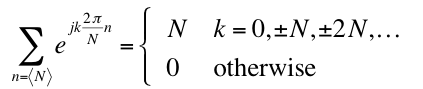


Problem .
Give an expression for the magnitude of a complex exponential with frequency φ, i.e., |ejφ|. Hint: it's a numeric value independent of φ.
Problem .
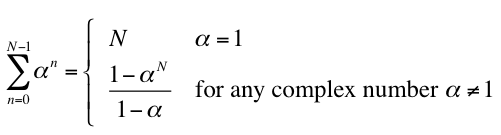
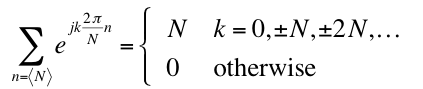
Problem .
Consider the following signals, which are periodic with period N. For each signal compute the spectral coefficients ak. In 6.02, we usually choose N consecutive k's starting with -N/2.
a-2 = -(1/2)j a-1 = (3/2) - (1/2j) = (3/2) + (1/2)j a0 = 1 a1 = (3/2) + (1/2j) = (3/2) - (1/2)j a2 = (1/2)j ak = 0 otherwiseNote the ak are periodic with period N, so, for example, aN = 1. For simplicity, we'll just list the spectal coefficients around 0.
In this example, the smallest N is 2:
x[n] = 5*cos(6(2π/2)n + π) + 7*cos(3(2π/2)n) = 5cos(π) + 7*cos(1(2π/2)n)Now we compute the two spectral coefficients (actually we can read them off the equation by inspection!):
a0 = -5 a1 = 7/2
ak = (1/N)Σn=<N>x[n]e-jk(2π/N)nYou can save yourself some work by remembering that ak is the complex conjugate of a-k when x[n] is real.
a-2 = (1 + -1)/4 = 0 a-1 = (1 + j)/4 a0 = (1 + 1)/4 = 1/2 a1 = (1 - j)/4
a-4 = j/4 a-2 = -j/4 a0 = 0 a2 = j/4 a4 = -j/4 ak = 0 otherwise
| ak | = | (1/N)Σn=<N>x[n]e-jk(2π/N)n |
= (1/N)|x[m]| | e-jk(2π/N)m |
= |x[m]|/N
since the magnitude of ejφ is 1 for any φ.
Problem .
If x[n] is real, even (i.e., x[n] = x[-n]) and periodic with period N, show that all the ak are real.
ak = (1/N)Σn=<N>x[n]e-jk(2π/N)nNoting that x[1] = x[-1], x[2] = x[-2], ..., if N is odd we can rewrite this as:
ak = (1/N)[x[0] + x[1](ejk(2π/N) + e-jk(2π/N)) + x[2](ejk(2π/N)2 + e-jk(2π/N)2) + ...] = (1/N)[x[0] + x[1]*2cos(2πk/N) + x[2]*2cos(4πk/N) + ...]which is a sum of real numbers. If N is even, there will be one negative index in the equation, n = -N/2, that won't be matched with a positive counterpart. But
x[-N/2]e-jk(2π/N)(-N/2) = x[-N/2]ejkπ = x[-N/2]*(-1)kwhich is also real.
Problem .
Suppose you're given the spectral coefficients ak for a particular periodic sequence x[n]. Compute the spectral coefficients bk for w[n] = x[n-α], i.e., x time shifted by α samples, in terms of the ak.
bk = (1/N)Σn=<N>w[n]e-jk(2π/N)n = (1/N)Σn=<N>x[n-α]e-jk(2π/N)nThis time, let's run the indicies of the summation from α to α+(N-1):
bk = (1/N)Σα ≤ n ≤ α+(N-1)x[n-α]e-jk(2π/N)n = (1/N)Σ0 ≤ n ≤ (N-1)x[n]e-jk(2π/N)(n+α) = (1/N)Σ0 ≤ n ≤ (N-1)x[n]e-jk(2π/N)ne-jk(2π/N)α = e-jk(2π/N)α(1/N)Σ0 ≤ n ≤ (N-1)x[n]e-jk(2π/N)n = ake-jk(2π/N)α
Problem .
Consider an LTI system characterized by the unit-sample response h[n].
Problem .
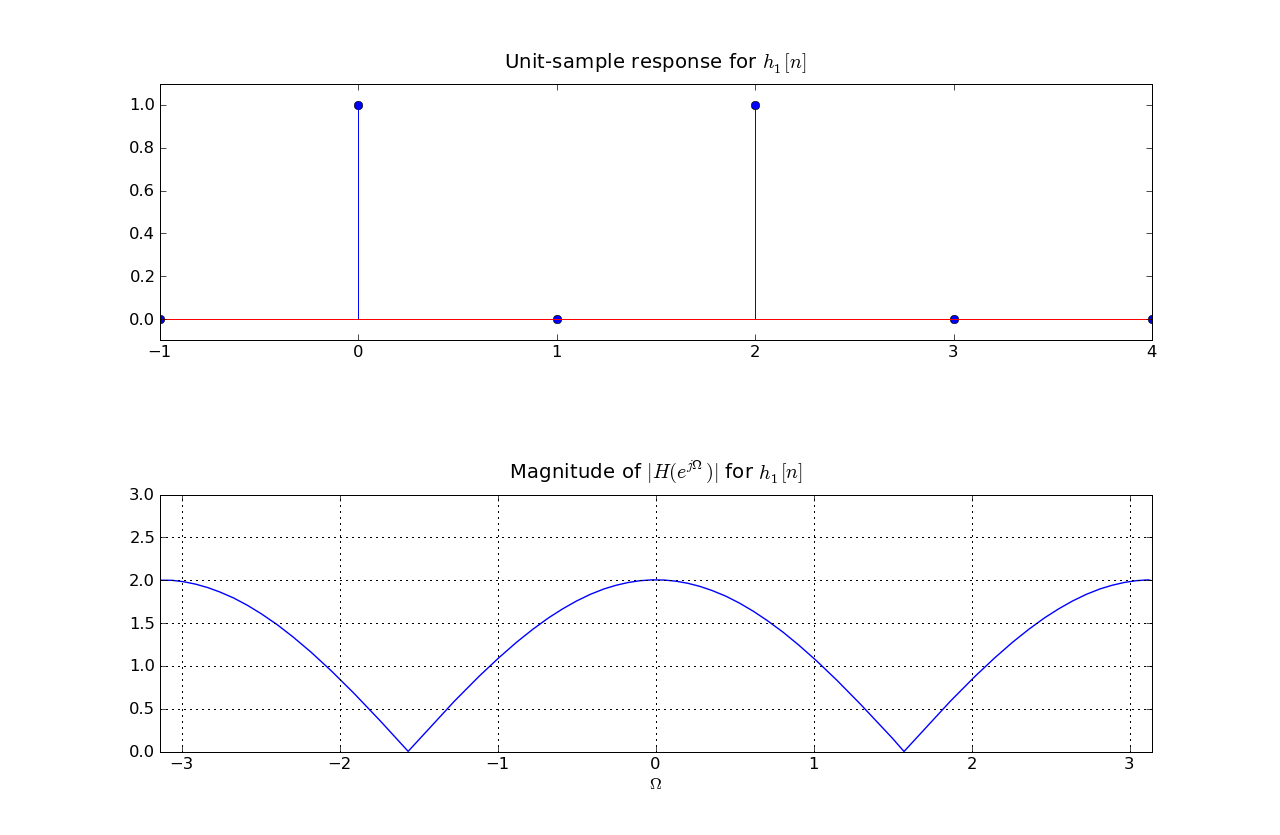
In answering the questions below, please consider the unit sample response and frequency response of two filters, H1 and H2, plotted below.
Note: the only nonzero values of unit sample response for H1 are : h1[0] = 1, h1[1]=0, h1[2]=1.
Note, the only nonzero values of unit sample response for H2 are : h2[0] = 1, h2[1]=-sqrt(3), h2[2]=1.
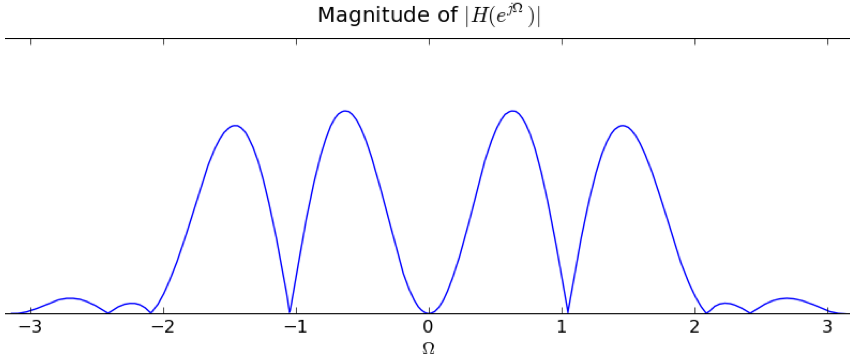
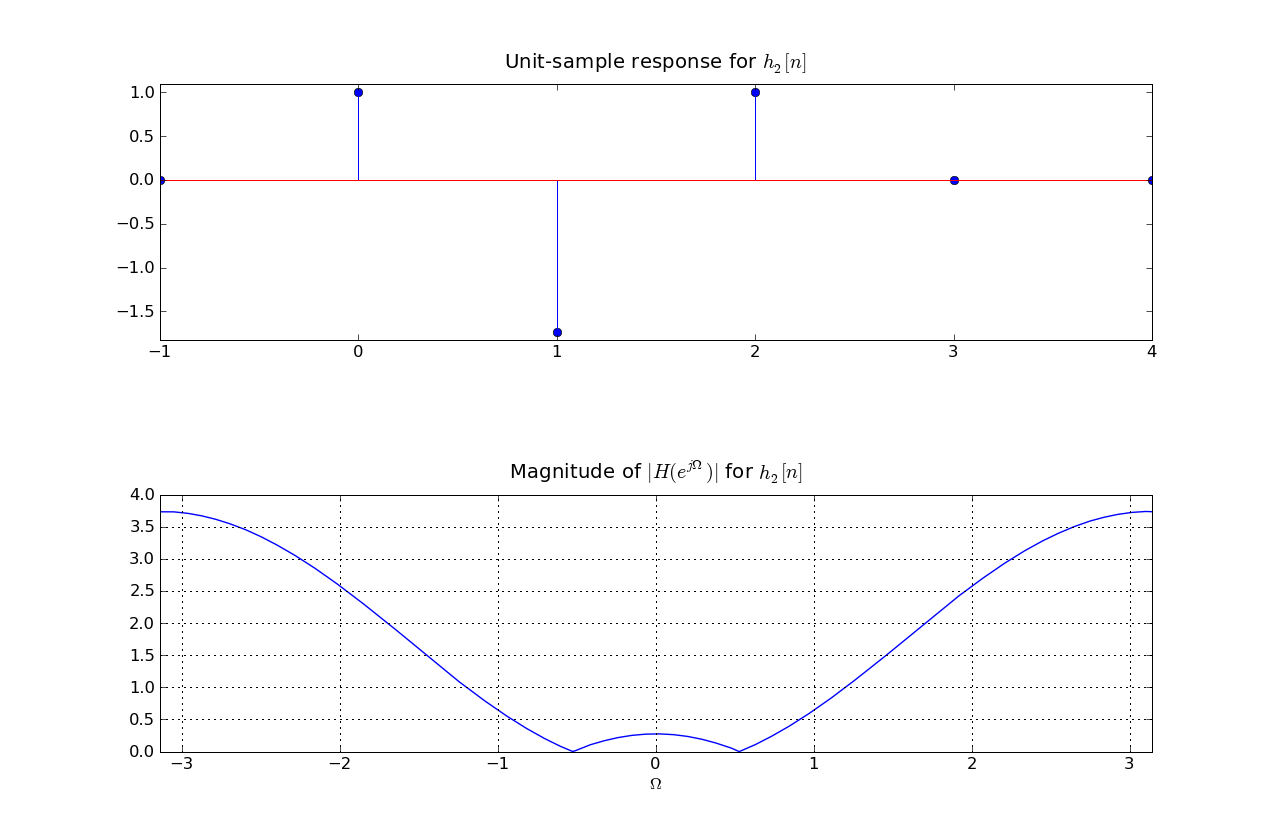
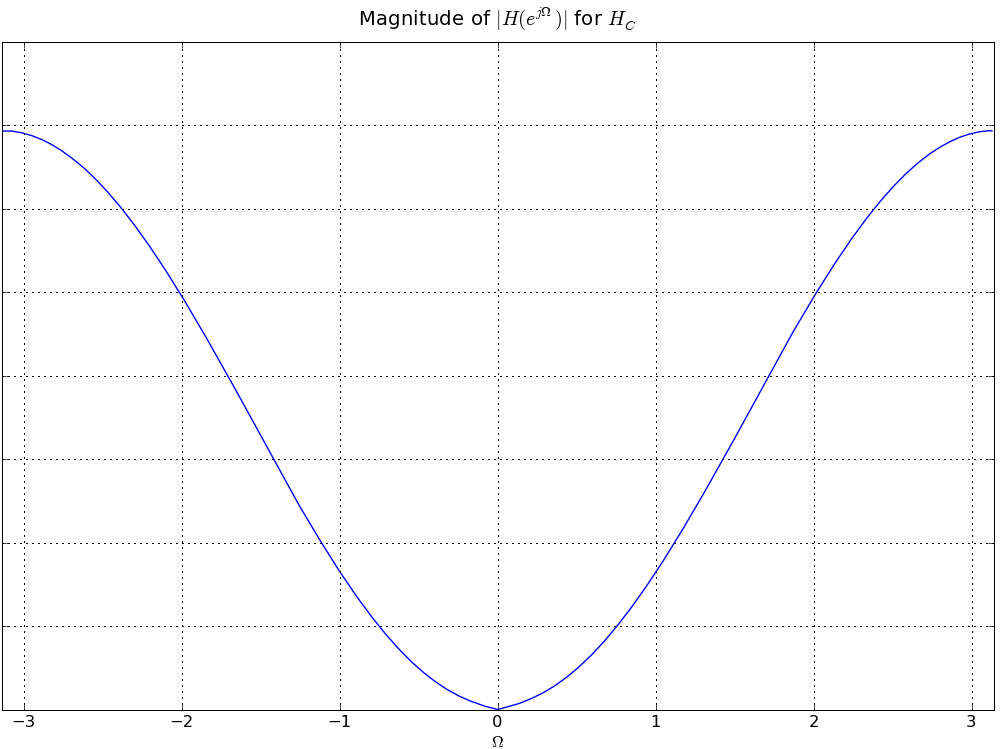
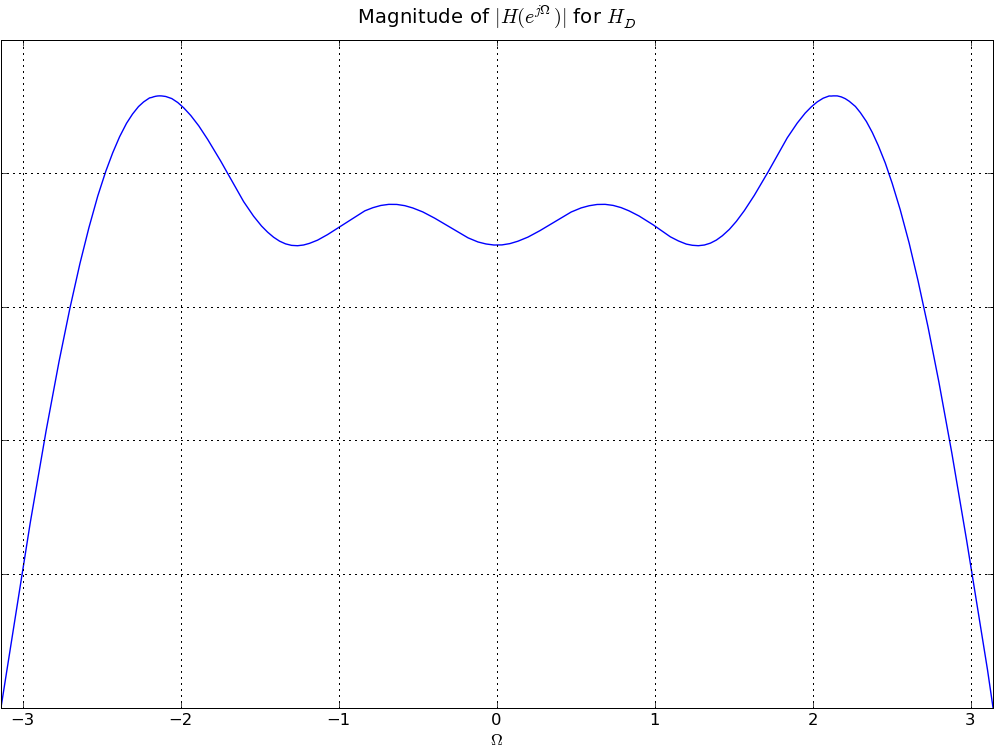
In answering the several parts of this review question consider four linear time-invariant systems, denoted A, B, C, and D, each characterized by the magnitude of its frequency response, |HA(ejΩ)|, |HB(ejΩ)|, |HC(ejΩ})|, and |HD(ejΩ)| respectively, as given in the plots below. This is a review problem, not an actual exam question, so similar concepts are tested multiple times to give you practice

h[n] = α δ[n] - h1[n]
and what is the numerical value of |α|?
|α|=2 as H1(ej0)=2 but HB(ej0)=0.
h[n] = Σmh1[m]h2[n-m] for m = 0 to n
and what are the numerical values of h[2], h[3] and H(ej0)?
H(ej0) = H1(ej0)H2(ej0) = 2(2 - sqrt(3)) = 4 - 2sqrt(3)
h[n] = [1,0,1]*[1,-sqrt(3),1] so h[2] = 2 and h[3] = -sqrt(3).
h[n] = α δ[n] - Σmh1[m]h2[n-m] for m = 0 to n
and what is the numerical value of |α|?
Since |HA(ejπ)| = |H1(ejπ)||H2(ejπ)|, |α| = 2(2 + sqrt(3)) = 4 + 2sqrt(3).
h[n] = α δ[n] - h2[n]
and what is the numerical value of |α|?
HC(ej0) = 0 so |α| = |H2(ej0)| = 2 - sqrt(3).
x[n]=0 for n < 0 and
x[n] = cos(nπ/6) + cos(nπ/2) + 1.0 for n ≥ 0
Which system (A, B, C or D) produced an output, y[n] below, and what is the value of y[n] for n > 10?
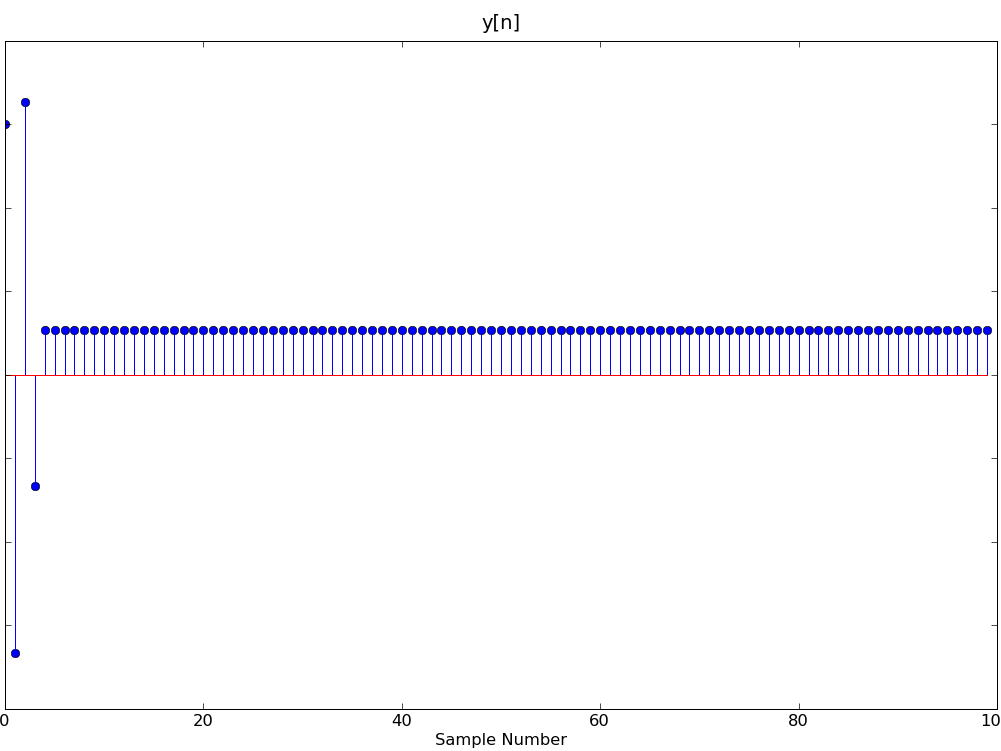
y[n] for n > 10 = |HA(ej0)|*1 = 4 - 2sqrt(3)
x[n]=0 for n < 0 and
x[n] = cos(nπ/6) + cos(nπ/2) + 1.0 for n ≥ 0
Which system (H1 or H2) produced an output, y[n] below, and what is the value of y[22]?
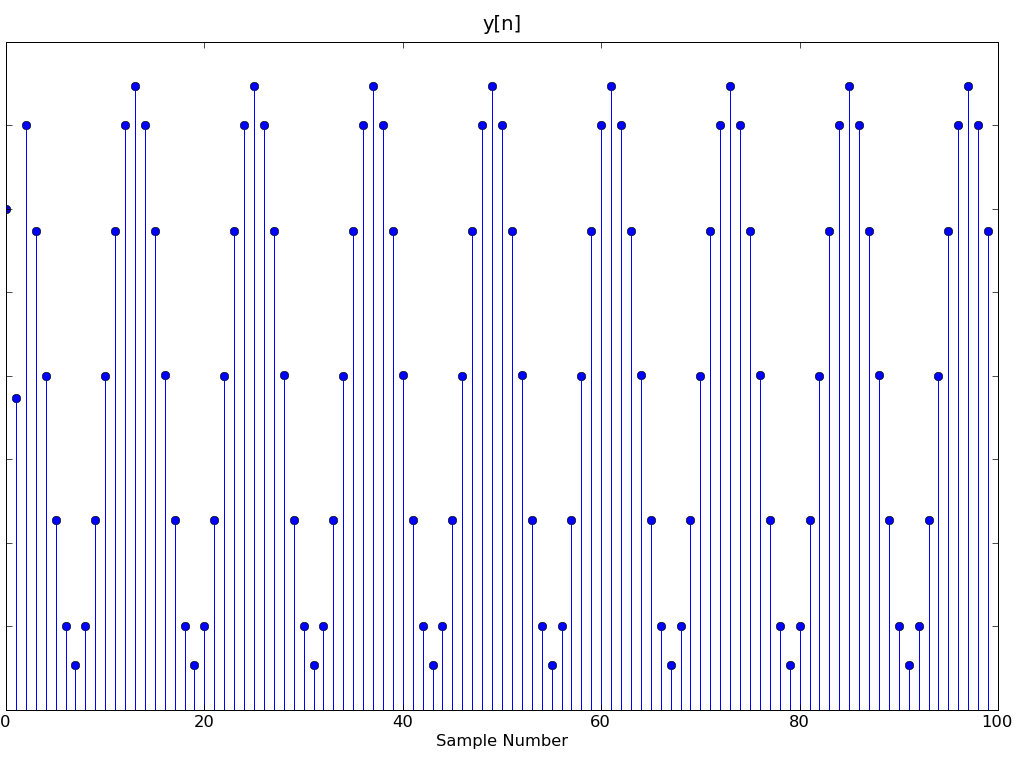
First compute some useful H's from the given h[n]:
H(ejΩ) = 1 + e-j2Ω H(ej0) = 1 + 1 = 2 H(ej(-π/6)) = 1 + ejπ/3 H(ej(π/6)) = 1 + e-jπ/3 H(ej(-π/2)) = 1 + ejπ = 1 - 1 = 0 H(ej(π/2)) = 1 + e-jπ = 1 - 1 = 0Now we can plug those into our equation for y[n] that uses the spectral coefficients for x[n] and the frequency response H:
y[n] = ΣkakH(ejk(2π/N))ejk(2π/N)n
= 2 + (1/2)H(ej(-π/6))ej(-π/6)n + (1/2)H(ej(π/6))ej(π/6)n
= 2 + (1/2)(1 + ejπ/3)ej(-π/6)n + (1/2)(1 + e-jπ/3)ej(π/6)n
= 2 + (1/2)ej(-π/6)n + (1/2)e-j((π/6)n - π/3) + (1/2)ej(π/6)n + (1/2)ej((π/6)n - π/3)
= 2 + cos((π/6)n) + cos((π/6)n - π/3)
So
y[22] = 2 + cos(22π/6) + cos(22π/6 - π/3)
= 2 + 0.5 - 0.5
= 2
Problem .
In answering the several parts of this question, consider three linear time-invariant filters, denoted A, B, and C, each characterized by the magnitude of their frequency responses, |HA(ejΩ)|, |HB(ejΩ)|, |HC(ejΩ)|, respectively, as given in the plots below.
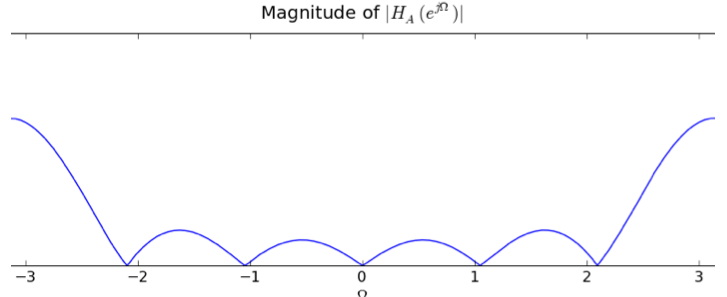

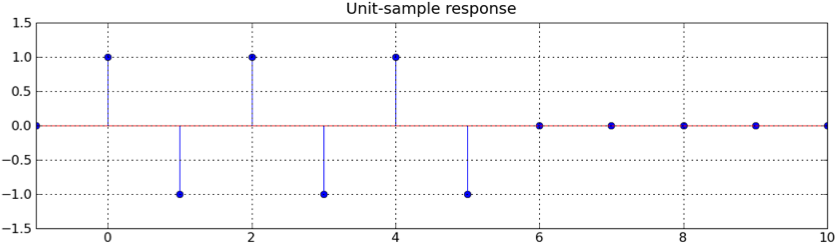
Ω=0: |H(ej0)| = |Σh[n](1)| = 0 Ω=π: |H(ejπ)| = |Σh[n](-1)n| = 6The only plot with a frequency response of 0 at frequency 0 and something non-zero at frequency π is the one for filter A.
Looking at the frequency response for A, it has its largest magnitude at ±π, which we calculated above to be 6.
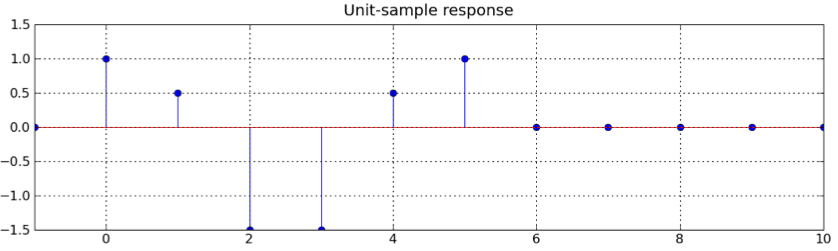
Ω=0: |H(ej0)| = |Σh[n]| = 1 + .5 - 1.5 - 1.5 + .5 + 1 = 0 Ω=π: |H(ejπ)| = |Σh[n](-1)n| = 1 -.5 - 1.5 + 1.5 +.5 - 1 = 0The only plot with a frequency response of 0 at frequencies 0 and π is the one for filter B.
The maximum magnitude of the frequency response is given by:
|H(ejΩ)| = |Σnh[n]e-jΩn| ≤ Σn|h[n]|(1) ≤ 6.So, no, it's not bigger than 6.
x[n] = cos((π/3)n) + cos(πn) + 1.0
Which filter (A, B,or C) produced the output, y[n] below, and what is maxΩ |H(ejΩ)| for your selected system?
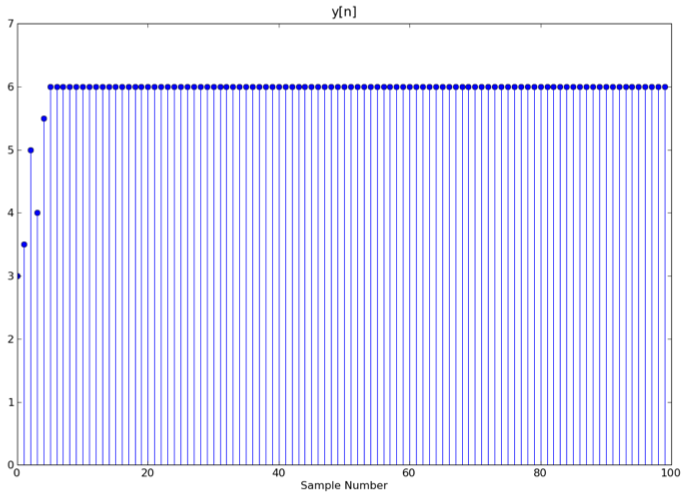
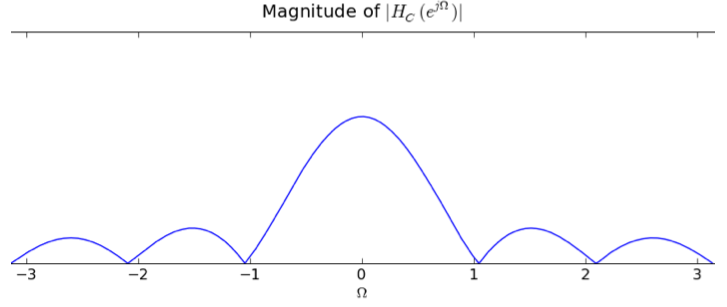
The only other component of x[n] is the constant 1, so that means that H(ej0) = 6 since constant inputs have frequency 0.
The only plot that satisfies these conditions is C. From the plot of C's frequency response, the maximum magnitude occurs at frequency 0 and has the value 6 as we calculated above.
Which of the six new filters has the frequency response plotted below?
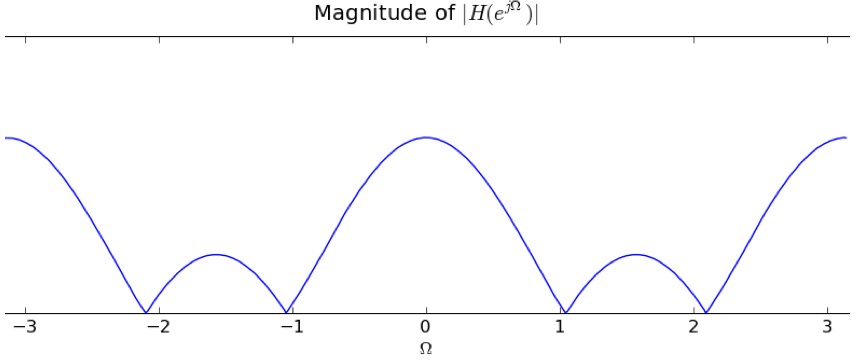
Which of the six new filters from the previous question has the frequency response plotted below?