6.02 Practice Problems: Modulation & Demodulation

Problem .

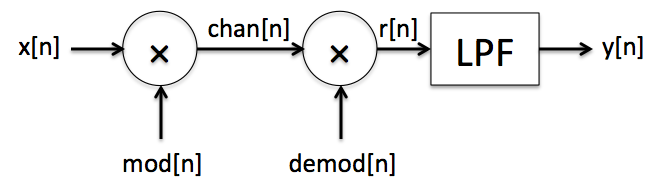
Here's our "standard" modulation-demodulation system diagram: at the transmitter, signal x[n] is modulated by signal mod[n] and the result (chan[n]) is sent to the receiver where the incoming signal is demodulated by demod[n] and sent through a low-pass filter to produce y[n].

Suppose the band-limited signal x[n] has the spectral coefficients shown below, where N=101:

1. Let mod[n] = cos(15(2π/101)n). Sketch a plot of the spectral coefficients for chan[n], showing both the real and imaginary components. Please label center frequencies and peak amplitudes.

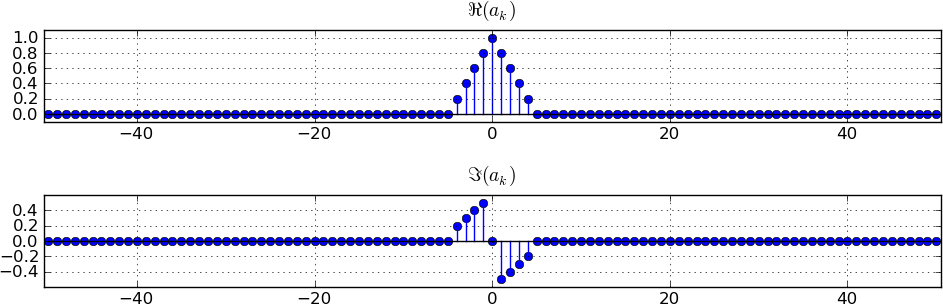
   Let us say we want to modulate by a cosine with discrete frequency component f . To get the representation of this modulated signal in the frequency domain we move the spectrum of the original signal x[n] to the left and to the right symmetrically by -f and +f respectively. In the process we also scale down the spectrum of the original signal by one-half before moving to the left and to the right. Here f is 15, so we get two triangles at 0+15 and 0-15 respectively.

   We can carry out the process independently for the real and imaginary components of the spectrum. In both cases we must remember to scale down by one-half. After carrying out these steps, we get the figures shown below.

   Another alternative to this graphical process is to remember a dual of the convolution theorem. Recall from the Chapter on Frequency Response that convolution in the time domain is equivalent to multiplication in the frequency domain. A dual of this result holds as well, where multiplication in the time domain is equivalent to convolution in the frequency domain. Modulation, if you look at it closely, is just multiplication in the time domain. So the resulting frequency spectra of the modulated signal can be obtained by convolving the frequency spectra. The process of convolution is the same as we described for time domain sequencues, we simply flip-slide and dot away.

2. Let demod[n] = cos(15(2π/101)n), i.e., a sinusuoid of the same frequency and phase as mod[n]. Sketch a plot of the spectral coefficients for r[n], showing both the real and imaginary components. Please label center frequencies and peak amplitudes.
   We apply the same procedure as in question A above. Look at the two triangles in the Real Part of the frequency spectrum from part A. Call them T and T'. Now T is moved to 15+15 and 15-15 and scaled down by 2. T' is moved to -15+15 and -15-15 and scaled down by 2 again. Since everything here is linear, we add the resulting shifted spectra. In particular, note how the waveforms around frequency 0 are added together to produce a center component that's twice the height of the two side components.

   

3. Give the appropriate cutoff frequency and gain for the low-pass filter LPF so that y[n] is identical to x[n].
   The figure above shows that there are exactly 4 non-zero frequency components around the origin in the base-band. Besides the shapes are scaled down by 2 compared to the original spectral representation of x[n]. Hence the low-pass filter should have a gain of 2 and a cutoff frequency that equals the bandwidth of x[n], i.e., k = ±5.

4. Let mod[n] = sin(15(2π/101)n), i.e., like part (A) except the modulating signal is a sine instead of a cosine. Sketch a plot of the spectral coefficients for chan[n], showing both the real and imaginary components. Please label center frequencies and peak amplitudes.

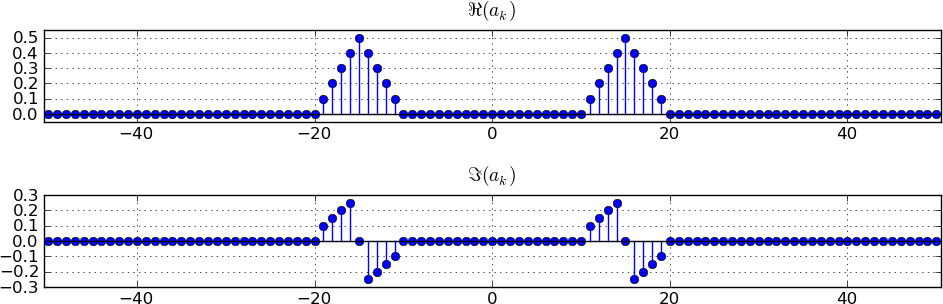
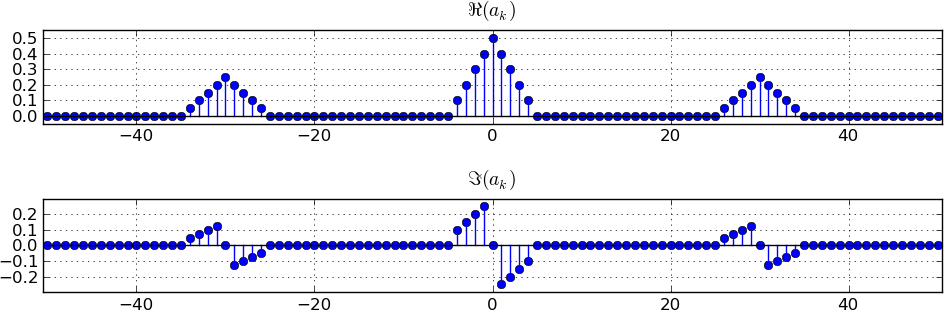
   The procedure for modulating with a sine is similar to the procedure for modulating with a cosine. However, instead of scaling each portion by a factor of 0.5, we scale the portion moving to 0+f with -j/2 and the portion moving to 0-f with +j/2. This implies that the real part of the spectrum of x[n] now appears in the complex part of the spectrum of the modulated signal and vice versa. The figure below shows the resulting spectrum. Note how the real and imaginary parts have been interchanged.

   Once again, if you prefer a more mathematical and less graphical approach, you can use convolution in the frequency domain as outlined earlier. If you are modulating by an sinusoid with arbitrary phase, you can break it up into a sine and a cosine and apply linearity to get the modulated signal spectrum.

   

5. Let demod[n] = cos(15(2π/101)n), i.e., a sinusuoid of the same frequency and but π/2 out of phase with mod[n]. Sketch a plot of the spectral coefficients for r[n], showing both the real and imaginary components. Please label center frequencies and peak amplitudes.
   This is just like Part B except that instead of reinforcing each other, the components at the origin perfectly cancel each other out. Note how the real and imaginary parts have been interchanged.

   

6. Assuming the parameters of the LPF are set as determined in part (C), describe y[n].
   y[n] = 0. Demodulating with a signal that's π/2 out of phase with the modulating signal produces destructive adding around frequency 0, so the signal in that region has zero amplitude. In the frequency domain, this result is evident by looking at the Figure from Part E: there are no baseband components remaining near the origin and hence the LPF returns nothing.

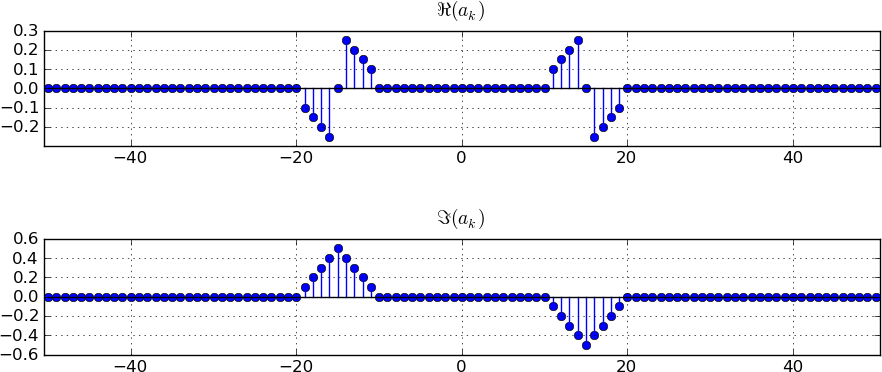
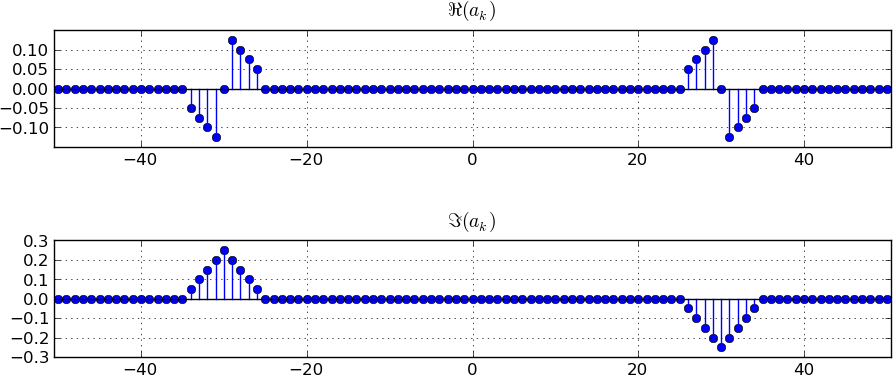
Problem . Single-sideband (SSB) modulation is a modulation technique designed to minimize the amount of footprint used to transmit an amplitude modulated signal. Here's one way to implement an SSB transmitter.

1. Starting with a band-limited signal s[n], modulate it with two carriers, one phase shifted by π/2 from the other. The modulation frequency is chosen to be B/2, i.e., in the middle of the frequency range of the signal to be transmitted. Sketch the real and imaginary parts of the Fourier coefficients for the signals at points A and B. The figure below shows the Fourier coefficients for the signal s[n].

   

   Use the same method as the previous question to get the spectrum of the modulated signal. Note that the two triangles overlap near the origin.

   

2. The modulated signal is now passed through a low-pass filter with a cutoff frequency of B/2. Sketch the real and imaginary parts of the Fourier coefficients for the signals at points C and D.
   Since the LPF cutoff is B/2, only frequency components with indices between 0 and B/2 survive and the rest are removed.

   

3. The signal is modulated once again to shift it up to the desired transmission frequency. Sketch the real and imaginary parts of the Fourier coefficients for the signals at points E and F.
   Note that both spectra have only the real part surviving. This is because C, whose spectra is purely real is modulated by a cosine with a purely real spectrum. Similarly, D's spectrum is purely imaginary and it is modulated by a sine with a purely imaginary spectrum , meaning that the resulting spectrum is once again real.

   

4. Finally the two signals are summed to produce the signal to be sent over the air. Sketch the real and imaginary parts of the Fourier coefficients for the signal at point G.
   Let's call the four triangles in the spectrum at E T1,T2,T3 and T4. We order them based on the x-coordinate of their third vertex ie the one not on the x-axis. Similarly, let the 4 triangles in the spectrum at F be F1,F2,F3 and F4 using the same ordering. When we add these two spectra. T1 and F1 cancel each other out, and so do T4 and F4. T2-F2 and T3-F3 both reinforce each other.

   

Problem .

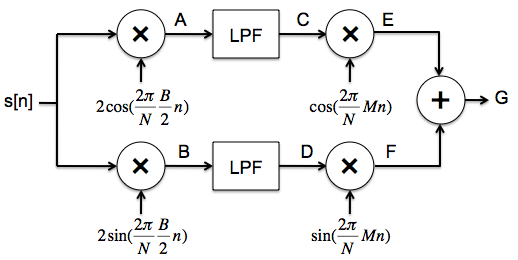
Consider the simple modulation-demodulation system below, where all signals are assumed periodic with period N = 10000 and the sampling frequency, fs, is 10000 samples per second. In addition, Ωa = 2π(fa/fs) = (1000*2π)/10000.

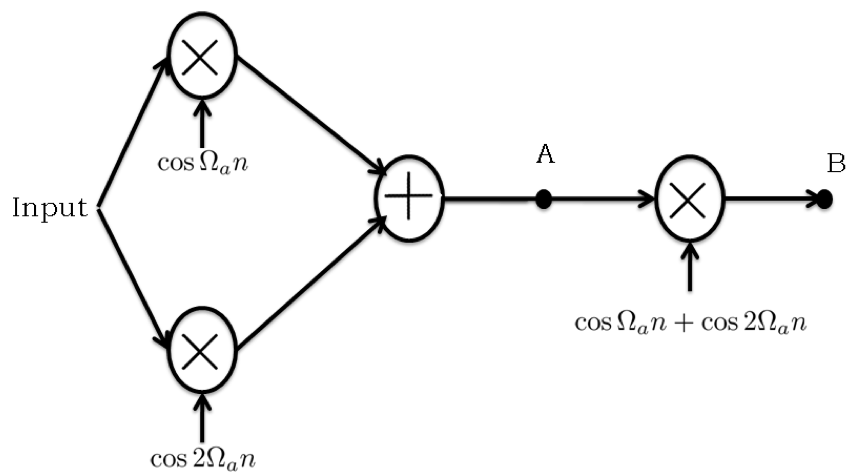
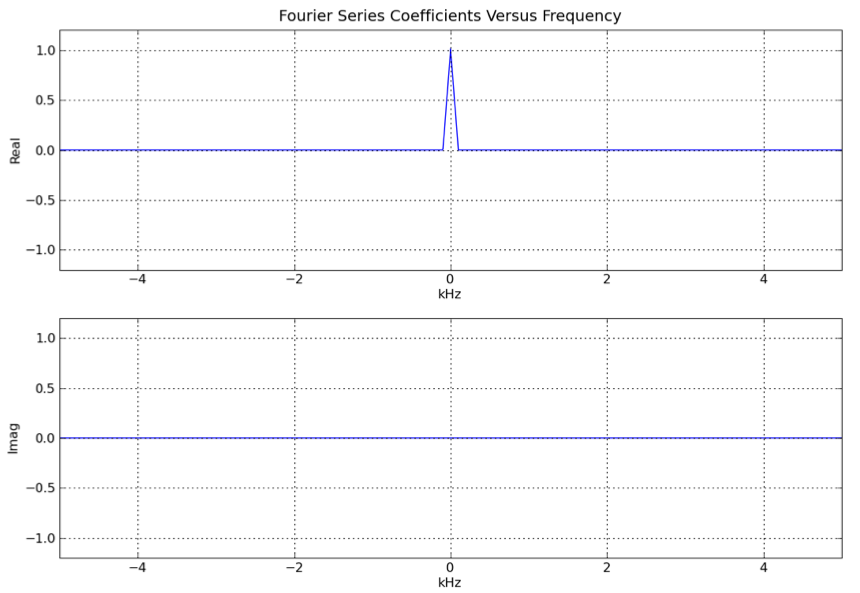
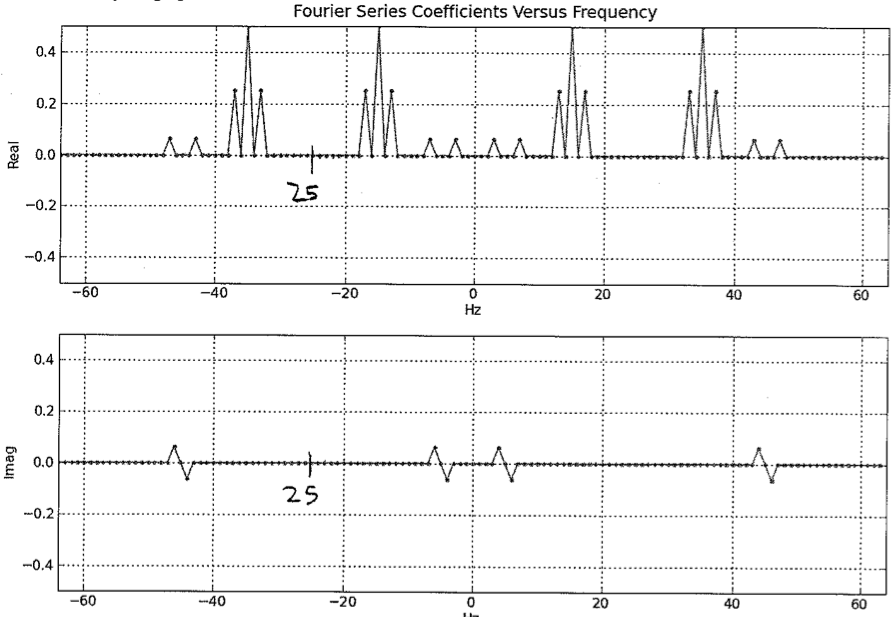
The Fourier Series coefficients versus frequency for the input to the modulation-demodulation system are plotted below for the case N=10000 and fs=10000. Note that the Fourier coefficients are nonzero only for -100 ≤ k ≤ 100.

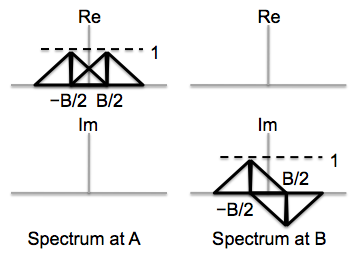
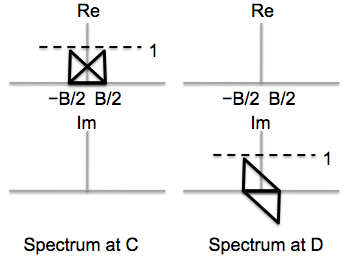
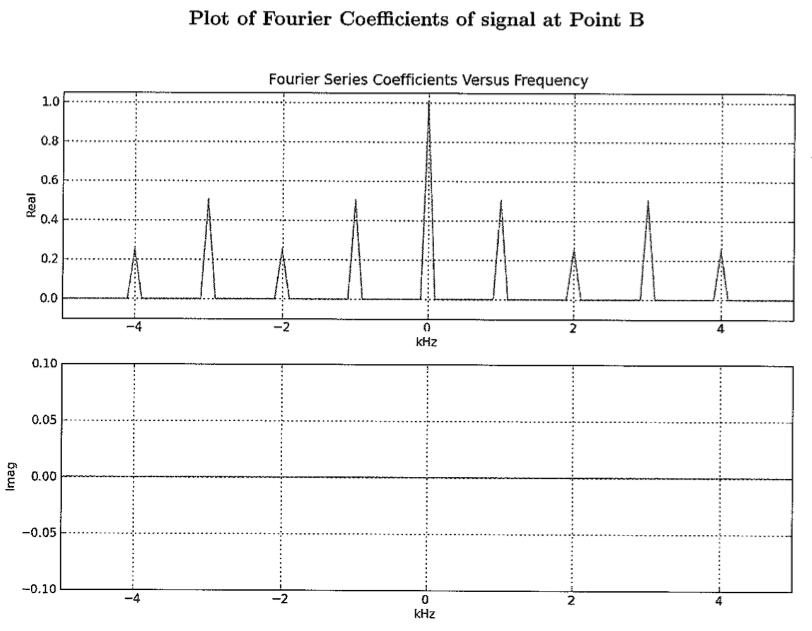
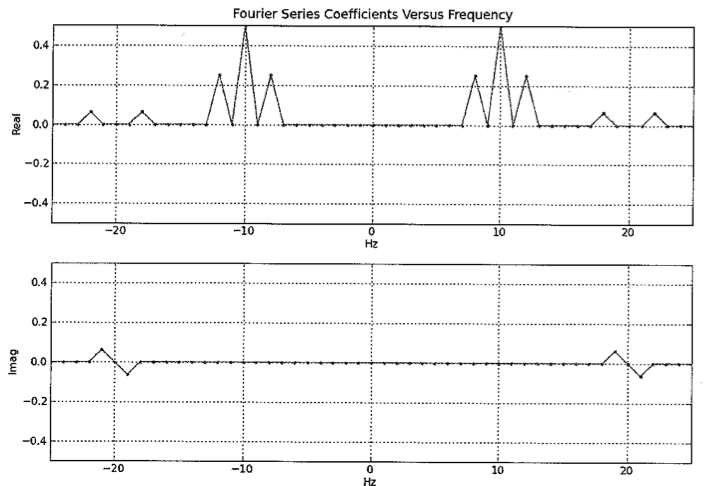
Please plot the Fourier series coefficients versus frequency for the signals at location A and B in the above diagram. Be sure to label key features such as values and coefficient indices for peaks. Also indicate the width of the peaks.

The signal is modulated by 2 carrier waves, a cosine at 1000 and a cosine at 2000. These two modulated spectra are then added up. The original signal spectrum is at the origin, so after modulation the spectral components appear at +/- 1000 and +/- 2000 respectively. The spectrum at A simply adds these two spectra and hence we get 4 peaks ie at +/- 1000 and +/- 2000. The height of the peak is one-half that of the original and the width remains the same as in the original signal ie 100Hz.

For the spectrum at B, each of the peaks in A's spectrum are shifted and scaled by each of the modulating components . There are 2 modulating components since we are multiplying by (cos Omega + cos 2 *Omega) . There are 4 peaks in A's original spectrum. So the resulting peaks are at frequencies
2000 + 2000 = 4000
2000 - 2000 = 0
1000 + 2000 = 3000
1000 - 2000 = -1000
2000 + 1000 = 3000
2000 - 1000 = 1000
1000 + 1000 = 2000
1000 - 1000 = 0
-2000 + 2000 = 0
-2000 - 2000 = -4000
-1000 + 2000 = 1000
-1000 - 2000 = -3000
-2000 + 1000 = -1000
-2000 - 1000 = -3000
-1000 + 1000 = 0
-1000 - 1000 = -2000
Each of these is scaled down by 2 wrt the original peak height, so each of these 8 has a height of 1/4. There are 2 peaks at 3000 which add up to give back a height of 1/2. Similarly at -3000, -1000 and +1000. Hence, all these peaks have height 1/2. This accounts for 4*2 = 8 peaks. 4 peaks are located at 0, and all of these add up to give a peak of height 1 at frequency 0. This accounts for 4 more peaks. The remaining 4 (16-4*2 - 4) are all "singleton" peaks at +/- 4000 and +/- 2000 respectively with height 1/4.

Problem .

In this modulation problem you will be examining periodic signals and their associated discrete-time Fourier series (DTFS) coefficients. Recall that a periodic signal x[n] with period N has DTFS coefficients given by

ak = (1/N)Σn=<N>x[n]e-jk(2π/N)n

and that the signal x[n] can be reconstructed from the DTFS coefficients using

x[n] = Σk=<N>akejk(2π/N)n

All parts of this question pertain to the following modulation-demodulation system, where all signals are periodic with period N = 10000. Please also assume that the sample rate associated with this system is 10000 samples per second, so that k is both a coefficient index and a frequency. In the diagram, the modulation frequency, km, is 500.

1. Suppose the DTFS coefficients for the signal y[n] in the modulation/demodulation diagram are as plotted below.

   

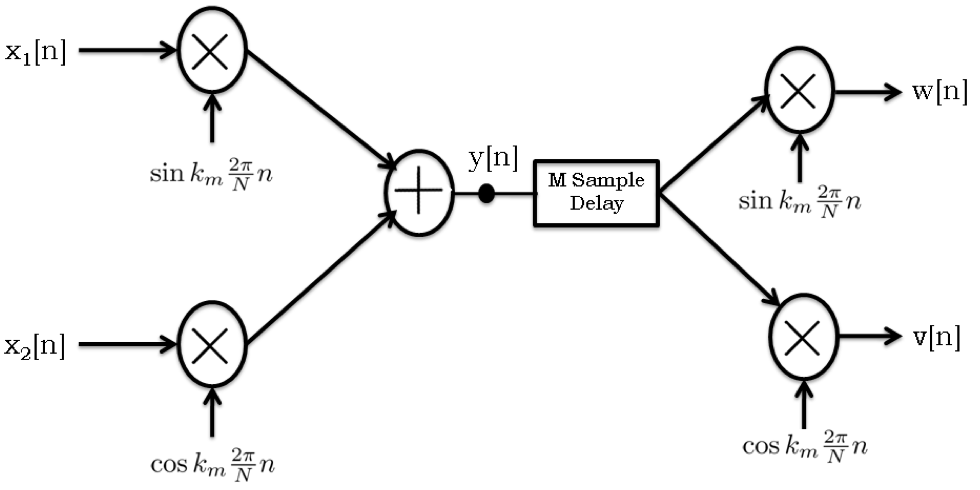
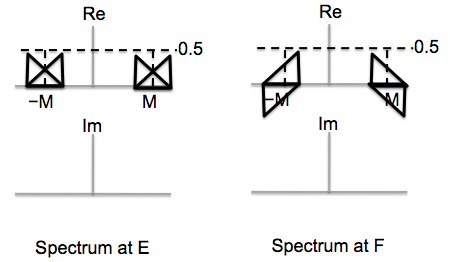
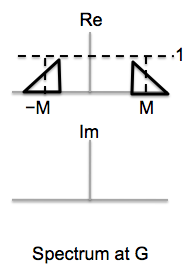
   Assuming that M = 0 for the M-sample delay (no delay), please plot the DTFS coefficients for the signals w and v in the modulation/demodulation diagram. Be sure to label key features such as values and coefficient indices for peaks.

   

   

2. Assuming the DTFS coefficients for the signal y[n] are the same as in part A, please plot the DTFS coefficients for the signal x1 in the modulation/demodulation diagram. Be sure to label key features such as values and coefficient indices for peaks.
   Work backwards from the modulated spectrum (spectrum of y[n]) to get the original signal. Follow the same intuition as has been explained in the earlier solutions.

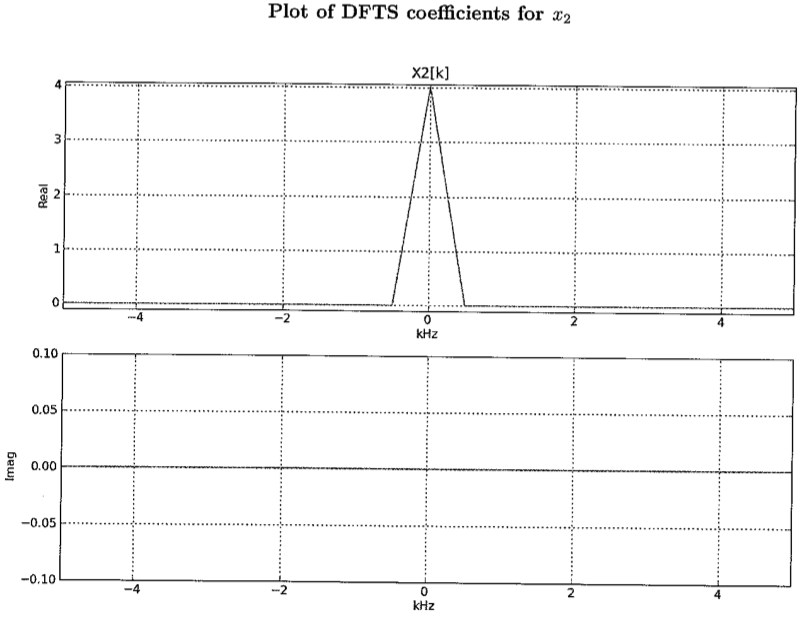
   For the record, above are the coefficients for x2[n]:

3. If the M-sample delay in the modulation/demodulation diagram has the right number of samples of delay, then it will be possible to nearly perfectly recover x1[n] by low-pass filtering v[n]. Please determine the smallest positive number of samples of delay that are needed and the cut-off frequency for the low-pass filter. Please be sure to justify your answer.
   We want to choose M such that

   sin(km(2π/N)(n-M)) ≈ cos(km(2π/N)n)
   

   i.e., M samples of delay should introduce a phase shift of +π/2, or, equivalently, -3π/2:

   -3π/2 = 500(2π/10000)(-M) = (-M)π/10
   

   So if M = 15 we get the desired result. Looking at the imaginary part of the plot in part (A), which shows x1[n] modulated by sin(...), we see that the bandwidth of x is 250 kHz.

   Note that if M=5, the phase shift is -π/2, which produces -cos(...), which we can convert to cos(...) if the LPF has a gain of -1.

Problem .

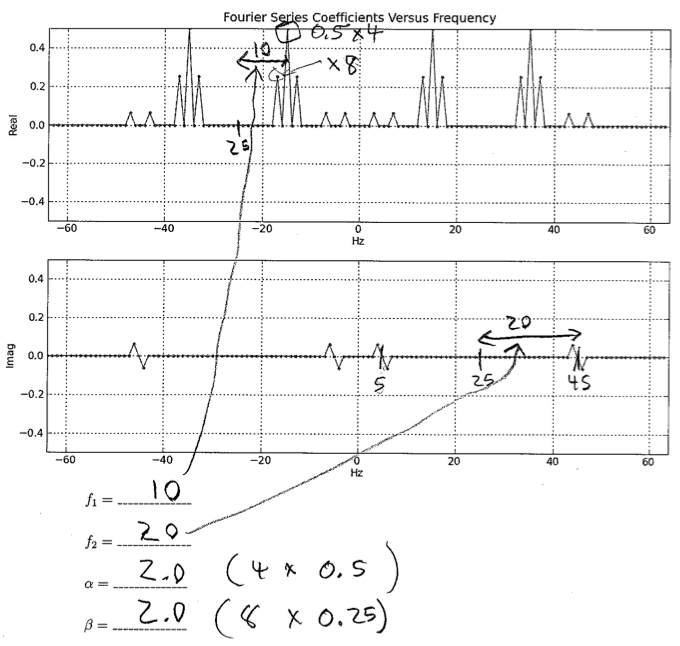
In answering this question, please refer to the modulation-demodulation system diagrammed below. Assume that N=128 and that the sampling frequency, fs, is 128 samples per second.

1. Below are the plots of the real and imaginary parts of the Fourier coefficients vs. frequency for point A of the modulation-demodulation diagram. Please plot the real and imaginary parts of the Fourier coefficients vs. frequency for the signal at point B, assuming f3 = 25. You only need to plot the Fourier coefficents in the range -25 to 25. Please be sure to label critical frequencies and values in your graph.

   

   

2. Referring to plot given in part (A), if

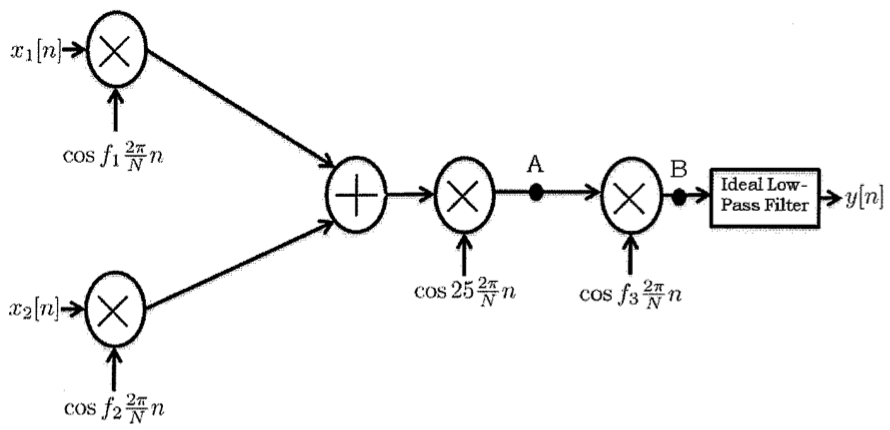
   x1[n] = α + βcos(2(2π/N)n) and
   x2[n] = (1/2)cos(2(2π/N)n) + (1/2)sin((2π/N)n)
   

   please determine the two modulation frequencies, f1 and f2, and the two amplitudes, α and β.

   

3. Now suppose

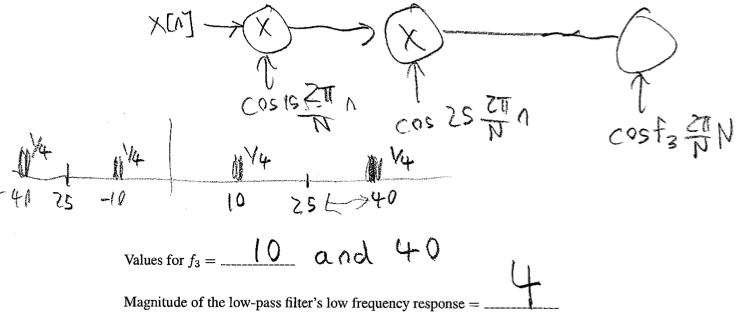
   x1[n] = (1/2)cos(2(2π/N)n) + (1/2)sin((2π/N)n)
   x2[n] = 0
   

   and f1 = 15 (not one of the answers to part B!). For what values of f3 < 64 (there is more than one) will y[n] = x1[n], assuming that the low-pass filter has been designed correctly? In addition, what should the magnitude be for the low frequency response of the low-pass filter?