Reading 18: Parsers

A parser generator is a good tool that you should make part of your toolbox. A parser generator takes a grammar as input and automatically generates a parser, which takes a sequence of characters and tries to match the sequence against the grammar.

The parser typically produces a parse tree, which shows how grammar productions are expanded into a sentence that matches the character sequence. The root of the parse tree is the starting nonterminal of the grammar. Each node of the parse tree expands into one production of the grammar. We’ll see how a parse tree actually looks later in this reading.

The final step of parsing is to do something useful with this parse tree. We are going to translate it into a value of a recursive data type. Recursive abstract data types are often used to represent an expression in a language, like HTML, or Markdown, or Java, or algebraic expressions. A recursive abstract data type that represents a language expression is called an abstract syntax tree (AST).

In 6.031, we are going to use ParserLib, a parser generator for Java developed by the course staff. The parser generator is similar in spirit to more widely used parser generators like Antlr, but it has a simpler interface and is generally easier to use.

Here is what our HTML grammar looks like as a ParserLib grammar:

root ::= html;
html ::= ( italic | normal ) *;
italic ::= '<i>' html '</i>';
normal ::= text; 
text ::= [^<>]+;  /* represents a string of one or more characters that are not < or > */

Let’s break it down.

Each ParserLib rule consists of a name, followed by a ::=, followed by its definition, terminated by a semicolon. The ParserLib grammar can also include Java-style comments, both single line and multiline.

By convention, we use lowercase for nonterminals: root, html, normal, italic, text. The ParserLib library is actually case-insensitive with respect to nonterminal names; internally, it canonicalizes names to all-lowercase, so even if you don’t write all your names into lowercase, you will see them as lowercase when you print your grammar.

Terminals are either quoted strings, like '<i>', or regular expressions, like [^<>]+.

root ::= html;

root is the entry point of this grammar, the nonterminal that the whole input needs to match. We don’t have to call it root. When we create a parser from the grammar, we will tell ParserLib which nonterminal to use as the entry point.

html ::= ( normal | italic ) *;

This rule shows that ParserLib rules can have the alternation operator |, the repetition operators * and +, and parentheses for grouping, in the same way we’ve been using in the grammars reading. Optional parts can be marked with ?, just like we did earlier, but this particular grammar doesn’t use ?.

italic ::= '<i>' html '</i>';
normal ::= text; 
text ::= [^<>]+;

Note that the text production uses the inverted character class [^<>], discussed in the grammars reading, to represent any character except < and >.

Consider the grammar shown below.

root ::= sum;
sum ::= primary ('+' primary)*;
primary ::= number | '(' sum ')';
number ::= [0-9]+;

This grammar will accept an expression like 42+2+5, but will reject a similar expression that has any spaces between the numbers and the + signs. We could modify the grammar to allow whitespace around the plus sign by modifying the production rule for sum like this:

sum ::= primary (whitespace* '+' whitespace* primary)*;
whitespace ::= [ \t\r\n]+;

However, this can become cumbersome very quickly once the grammar becomes more complicated. ParserLib allows a shorthand to indicate that certain kinds of characters should be skipped.

//The IntegerExpression grammar
@skip whitespace {
    root ::= sum;
    sum ::= primary ('+' primary)*;
    primary ::= number | '(' sum ')';
}
whitespace ::= [ \t\r\n]+;
number ::= [0-9]+;

The @skip whitespace notation indicates that any text matching the whitespace nonterminal should be skipped in between the parts that make up the definitions of sum, root, and primary. Two things are important to note. First, there is nothing special about whitespace. The @skip directive works with any nonterminal defined in the grammar. Second, note how the definition of number was intentionally left outside the @skip block. This is because we want to accept expressions with extra space around the operators, like 42 + 2, but we want to reject spaces within numbers, like 4 2 + 2.

The rest of this reading will use as a running example the IntegerExpression grammar defined just above, which we’ll store in a file called IntegerExpression.g.

The ParserLib parser generator tool converts a grammar like IntegerExpression.g into a parser. In order to do this, you need to follow three steps. First, you need to import the ParserLib library, which resides in a package lib6005.parser:

import lib6005.parser.*;

The second step is to define an Enum type that contains all the nonterminals used by your grammar. This will tell the compiler which definitions to expect in the grammar and will allow it to check for any missing ones.

private enum IntegerGrammar {
  ROOT, SUM, PRIMARY, NUMBER, WHITESPACE
};

Note that ParserLib itself is case insensitive, but by convention, the names of enum values are all upper case.

From within your code, you can create a Parser by calling its compile static factory method.

Parser<IntegerGrammar> parser = 
    Parser.compile(new File("src/intexpr/IntegerExpression.g"),
                   IntegerGrammar.ROOT);

This code opens the file IntegerExpression.g, using its path relative to the root project folder, and compiles it into a Parser object. Whether the grammar is in a string or a file, the compile method takes as a second argument the name of the nonterminal to use as the entry point of the grammar; root in the case of this example.

Assuming you don’t have any syntax errors in your grammar, the result will be a Parser object that can be used to parse text. Notice that the Parser is a generic type that is parameterized by the enum you defined earlier.

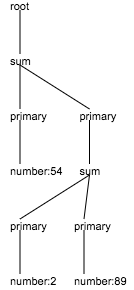
Now that you’ve generated the parser object, you are ready to parse your own text. The parser has a method called parse that takes in the text to be parsed (in the form of either a String, an InputStream, a File or a Reader) and returns a ParseTree. Calling it produces a parse tree:

ParseTree<IntegerGrammar> tree = parser.parse("54+(2+ 89)");

Note that the ParseTree is also a generic type that is parameterized by the enum type IntegerGrammar.

For debugging, we can then print this tree out:

System.out.println(tree.toString());

You can also try calling the method Visualizer.showInBrowser(tree) which will attempt to open a browser window that will show you a visualization of your parse tree. If for any reason it is not able to open the browser window, the method will print a URL to the console which you can copy and paste to your browser to view the visualization.

So we’ve used the parser to turn a stream of characters into a parse tree, which shows how the grammar matches the stream. Now we need to do something with this parse tree. We’re going to translate it into a value of a recursive abstract data type.

The first step is to learn how to traverse the parse tree. The ParseTree object has four methods that you need to be most familiar with. Three of them are fundamental observers:

/**
 * Get this node's name.
 * @return the nonterminal corresponding to this node in the parse tree.
 */
public NT name();

/**
 * Get this node's children.
 * @return the children of this node, in order, excluding @skipped subtrees
 */
public List<ParseTree<NT>> children();

/**
 * Get this subtree's text.
 * @return the substring of the original string that this subtree matched
 */
public String text();

Additionally, you can query the ParseTree for all children that match a particular production rule:

/**
 * Get the children that correspond to a particular production rule 
 * @param name Name of the nonterminal corresponding to the desired production rule.
 * @return children that represent matches of name's production rule.
 */
public List<ParseTree<NT>> childrenByName(NT name);

Note that like the Parser itself, the ParseTree is also parameterized by the type NT, an enum type that lists all the symbols in the grammar.

A good way to visit the nodes in a parse tree is to write a recursive function. For example, the recursive function below prints all nodes in the parse tree with proper indentation.

/**
 * Traverse a parse tree, indenting to make it easier to read.
 * @param node   parse tree to print.
 * @param indent indentation to use.
 */
void printAllNodes(ParseTree<IntegerGrammar> node, String indent){
    if (p.children().isEmpty()) {
        System.out.println(indent + p.name() + ":" + p.text());
    } else {
        System.out.println(indent + p.name());
        for (ParseTree<IntegerGrammar> child: p.children()){
            printAllNodes(child, indent + "   ");
        }
    }
}

We need to convert the parse tree into a recursive data type. Here’s the definition of the recursive data type that we’re going to use to represent integer arithmetic expressions:

IntegerExpression = Number(n:int)
                    + Plus(left:IntegerExpression, right:IntegerExpression)

If this syntax is mysterious, review recursive data type definitions.

When a recursive data type represents a language this way, it is often called an abstract syntax tree. An IntegerExpression value captures the important features of the expression – its grouping and the integers in it – while omitting unnecessary details of the sequence of characters that created it.

By contrast, the parse tree that we just generated with the IntegerExpression parser is a concrete syntax tree. It’s called concrete, rather than abstract, because it contains more details about how the expression is represented in actual characters. For example, the strings 2+2, ((2)+(2)), and 0002+0002 would each produce a different concrete syntax tree, but these trees would all correspond to the same abstract IntegerExpression value: Plus(Number(2), Number(2)).

Now, we can create a simple recursive function that walks the ParseTree to produce an IntegerExpression as follows:

    /**
     * Convert a parse tree into an abstract syntax tree.
     * 
     * @param parseTree constructed according to the grammar in IntegerExpression.g
     * @return abstract syntax tree corresponding to parseTree
     */
    private static IntegerExpression makeAbstractSyntaxTree(final ParseTree<IntegerGrammar> parseTree) {

        switch (parseTree.name()) {
        case ROOT: // root ::= sum;
            {
                final ParseTree<IntegerGrammar> child = parseTree.children().get(0);
                return makeAbstractSyntaxTree(child);
            }

        case SUM: // sum ::= primary ('+' primary)*;
            {
                final List<ParseTree<IntegerGrammar>> children = parseTree.children();
                IntegerExpression expression = makeAbstractSyntaxTree(children.get(0));
                for (int i = 1; i < children.size(); ++i) {
                    expression = new Plus(expression, makeAbstractSyntaxTree(children.get(i)));
                }
                return expression;
            }

        case PRIMARY: // primary ::= number | '(' sum ')';
            {
                final ParseTree<IntegerGrammar> child = parseTree.children().get(0);
                // check which alternative (number or sum) was actually matched
                switch (child.name()) {
                case NUMBER:
                    return makeAbstractSyntaxTree(child);
                case SUM:
                    return makeAbstractSyntaxTree(child); // in this case, we do the
                                                          // same thing either way
                default:
                    throw new AssertionError("should never get here");
                }
            }

        case NUMBER: // number ::= [0-9]+;
            {
                final int n = Integer.parseInt(parseTree.text());
                return new Number(n);
            }

        default:
            throw new AssertionError("should never get here");
        }

    }

The function follows the structure of the grammar, handling each rule from the grammar in turn: root, sum, primary, and number. The only rule we don’t need to handle here is whitespace, because the grammar uses whitespace only in a @skip block, and skipped subtrees are not returned by children() so they should never appear in the traversal.

An important thing to note is that there is a very strong assumption that the code will process a ParseTree that corresponds to the grammar in IntegerExpression.g. If you change the grammar, this code will likely fail.

Plus(Plus(Number(1), Number(2)), 
     Plus(Number(3), Number(4)))

@skip spaces { 
  date ::= monthname day ',' year | day '/' monthnum '/' year ;
}
monthname ::= 'January' | 'February' ;
monthnum ::= [0-9]+ ; 
day ::= [0-9]+ ;
year ::= [0-9]+ ;
spaces ::= ' '+ ;

@skip spaces { 
  list ::= int (',' list)? 
  int ::= '-'? [0-9]+ ;
}
spaces ::= ' '+ ;

enum ListGrammar  { LIST, INT };
static List<Integer> makeList(ParseTree<ListGrammar> parseTree) {
    switch (parseTree.name()) {
    case LIST:
        List<Integer> list = new ArrayList<>();
        list.add(Integer.parseInt(parseTree.▶▶A◀◀));
        if (parseTree.▶▶B◀◀ > 1) {
            list.addAll(makeList(parseTree.▶▶C◀◀));
        }
        return list;
    default:
        throw new AssertionError("should never get here");
    }


}

Several things can go wrong when parsing.

• Your grammar file may fail to open.
• Your grammar may be syntactically incorrect.
• The string you are trying to parse may not be parseable with your given grammar, either because your grammar is incorrect, or because your string is incorrect.

In the first case, the compile method will throw an IOException. In the second case, it will throw an UnableToParseException. In the third case, the UnableToParseException will be thrown by the parse method. The UnableToParseException exception will contain some information about the possible location of the error, although parse errors are sometimes inherently difficult to localize, since the parser cannot know what string you intended to write, so you may need to search a little to find the true location of the error.

ParserLib works by generating a top-down Recursive Descent Parser. These kind of parsers have a few limitations in terms of the grammars that they can parse. There are two in particular that are worth pointing out.

Left recursion. A recursive descent parser can go into an infinite loop if the grammar involves left recursion. This is a case where a definition for a nonterminal involves that nonterminal as its leftmost symbol. For example, the grammar below includes left recursion because one of the possible definitions of sum is sum '+' number which has sum as its leftmost symbol.

sum ::= number | sum '+' number;
number ::= [0-9]+;

Left recursion can also happen indirectly. For example, changing the grammar above to the one below does not address the problem because the definition of sum still indirectly involves a symbol that has sum as its first symbol.

sum ::= number | thing number;
thing ::= sum '+';
number ::= [0-9]+;

If you give any of these grammars to ParserLib and then try to use them to parse a symbol, ParserLib will fail with an UnableToParseException listing the offending nonterminal.

There are some general techniques to eliminate left recursion; for our purposes, the simplest approach will be to replace left recursion with repetition (*), so the grammar above becomes:

sum ::= (number '+')* number;
number ::= [0-9]+;

Greediness. This is an issue that you will probably not run into in this class, but it is a limitation of ParserLib you should be aware of. The ParserLib parsers are greedy in that at every point they try to match a maximal string for any rule they are currently considering. For example, consider the following grammar.

root ::= ab threeb;
ab ::= 'a'*'b'*
threeb ::= 'bbb';

The string 'aaaabbb' is clearly in the grammar, but a greedy parser cannot parse it because it will try to parse a maximal substring that matches the ab symbol, and then it will find that it cannot parse threeb because it has already consumed the entire string. Unlike left recursion, which is easy to fix, this is a more fundamental limitation of the type of parser implemented by ParserLib, but as mentioned before, this is not something you should run into in this class.

The topics of today’s reading connect to our three properties of good software as follows:

• Safe from bugs. A grammar is a declarative specification for strings and streams, which can be implemented automatically by a parser generator. These specifications are often simpler, more direct, and less likely to be buggy than parsing code written by hand.

• Easy to understand. A grammar captures the shape of a sequence in a form that is compact and easier to understand than hand-written parsing code.

• Ready for change. A grammar can be easily edited, then run through a parser generator to regenerate the parsing code.