The Chord protocol supports just one operation: given a key, it will determine the node responsible for storing the key's value. Chord does not itself store keys and values, but provides primitives that allow higher-layer software to build a wide variety of storage system; CFS is one such use of the Chord primitive. In this section, we provide a short summary of the Chord protocol so that the reader has sufficient background to follow the rest of the paper.
Each machine acting as a Chord server has a unique 160-bit Chord node identifier, produce by a SHA-1 hash of the node's IP address. Chord views the IDs as occupying a circular identifier space. Hash keys are also mapped into this identifier space, by hashing them to 160-bit key identifiers. Chord defines the node responsible for a key to be that key's ``successor.'' The successor of a key or node identifier j is the node with the smallest ID that is greater than or equal to j. Chord's primary task is to find these successors.

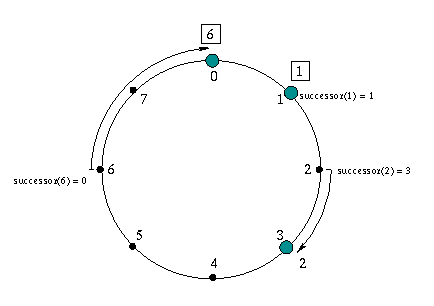
The above figure shows a simple example of a Chord network consisting of three nodes whose identifiers are 0, 1, and 3. The set of keys (or more precisely, keys' identifiers) is {1, 2, 6}, and they are assigned to the three nodes. Because the successor of key 1 among the nodes in the network is node 1, key 1 is assigned to node 1. Similarly, the successor of key 2 is 3, the first node found moving clockwise from 2 on the identifier circle. For key 6, the successor (node 0) is found by wrapping around the circle, so key 6 is assigned to node 0.
This hashing scheme was designed to let nodes enter and leave the network with minimal disruption. To maintain the consistent hashing mapping when a node n joins the network, certain keys previously assigned to n's successor become assigned to n. When node n leaves the network, all of its assigned keys are reassigned to n's successor. No other changes in the assignment of keys to nodes need occur. In the example above, if a node were to join with identifier 6, it would capture the key with identifier 6 from the node with identifier 7.
This hashing function is straightforward to implement (with the same constant-time operations as standard hashing) in a centralized environment where all machines are known. However, such a system does not scale. Therefore, the Chord protocol uses a distributed hash function, in which each node maintains a small routing table.
Each node, n, maintains a routing table with 160 entries, called the finger table. The ith entry in the table at node n contains the identity of the first node, s, that succeeds n by at least 2^(i-1) on the identifier circle, i.e., s = successor(n + 2^(i - 1)), where 1 ≤ i ≤ 160 (and all arithmetic is modulo 2^160). The node s is called the ith finger of node n, and denoted by n.finger[i].node. The first finger of n is its immediate successor on the circle. In addition, the ith finger table entry of node n contains the interval, [n.finger[i].node, n.finger[i+1].node), called the ith finger interval of node n, and denoted by n.finger[i].interval.
When a node n does not know the successor of a key k, it sends a ``find successor'' request to a intermediate node whose ID is closer to k. Node n finds the intermediate node by searching its finger table for the closest finger f preceding k, and sends the find successor request to f. Node f looks in its finger table for the closest entry preceding k, and sends that back to n. As a result n learns about nodes closer and closer to the target ID.
Consider again the example pictured above. Suppose node 3 wants to find the successor of identifier 1. Since 1 belongs to the circular interval [7, 3), it belongs to 3.finger[2].interval; node 3 therefore checks the second entry in its finger table, which is 0. Because 0 precedes 1, node 3 will ask node 0 to find the successor of 1. In turn, node 0 will infer from its finger table that 1's successor is the node 1 itself, and return node 1 to node 3.
In general, a Chord lookup proceeds in multiple hops around the identifier ring. Each hop eliminates at least half of the remaining distance to the desired successor. This means that the hops early in a query's path travel long distances in identifier space, and later hops travel small distances. Lookups take a number of hops proportional to the log of the number of nodes in the system. For each hop, the node doing the lookup sends a find successor message, and waits for the result; the result tells it where to send the next find successor message.
Given that the system is in a stable state, the Chord protocol needs to perform three operations: (1) initialize the predecessor and fingers; (2) update the fingers and predecessors of existing nodes to reflect the change in the network topology caused by the addition of n; and (3) copy all keys for which node n has became their successor to n.
A new node r can initialize its finger table by querying an existing node for the respective successors of the lower endpoints of the k intervals in r's table. Nodes whose routing information is invalidated by r's addition are determined using r's predecessor table.