Next: Information Content Previous: Which Attribute Is Best?
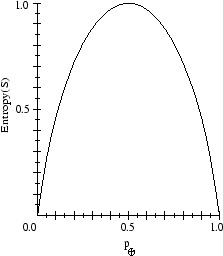
Entropy
is a sample of training examples
is the proportion of positive examples in
is the proportion of negative examples in
- Entropy measures the impurity of
= expected number of bits needed to encode class (
or
) of randomly drawn element of
(under the optimal, shortest-length code)
- Information theory: optimal length code assigns
bits to message of probability
.
So, expected number of bits to encode or
of random element
of
: