Measuring information

Someone picks a name out of a hat known to contain the names of 5 women and 3 men, and tells you a man has been selected. How much information have they given you about the selection? There are 8 names to start with and knowing the selection is a man narrows the choices down to 3 names. Using the formula from lecture with N = 8 and M = 3, we've been given log₂(8/3) bits of information.

Alternatively, the probability of drawing a man's name is p_man = 3/8, so the amount of information received is log₂(1/p_man) = log₂(1/(3/8)) = log₂(8/3). You're given a standard deck of 52 playing cards that you start to turn face up, card by card. So far as you know, they're in completely random order. How many new bits of information do you get when the first card is flipped over? The fifth card? The last card? Before the first card was flipped over there are 52 choices for what we'll see on the first flip. Turning the first card over narrows the choice down to a single card, so we've received log₂(52/1) bits of information.

After flipping over 4 cards, there are 48 choices for the next card, so flipping over the fifth card gives us log₂(48/1) bits of information.

Finally if all but one card has been flipped over, we know ahead of time what the final card has to be so we don't receive any information from the last flip. Using the formula, there is only 1 "choice" for the card before the card is flipped and we have the same "choice" afterwards, so, we receive log₂(1/1) = 0 bits of information. X is an unknown N-bit binary number (N > 3). You are told that the first three bits of X of 011. How many bits of information about X have you been given? Since we were told about 3 bits of X it would make sense intuitively that we've been given 3 bits of information! Turning to the formulas: there are 2^N N-bit binary numbers and 2^N-3 N-bit binary numbers that begin with 011. So we've been given log₂(2^N/2^N-3) = log₂(2³) = 3 bits of information (whew!). X is an unknown 8-bit binary number. You are given another 8-bit binary number, Y, and told that the Hamming distance between X and Y is one. How many bits of information about X have you been given? Before we learn about Y, there are 2⁸ = 256 choices for X. If the Hamming distance between X and Y is one that means that X and Y differ in only one of their 8 bits, i.e., for a given Y there are only eight possible choices for X. So we've been given log₂(256/8) = 5 bits of information. Variable length encoding & compression Huffman and other coding schemes tend to devote more bits to the coding of

(A) symbols carrying the most information, i.e., the symbols that are less likely to occur. This makes sense: to keep messages as short as possible, frequently occuring symbols should be encoded with fewer bits and infrequent symbols with more bits. Consider the following two Huffman decoding tress for a variable-length code involving 5 symbols: A, B, C, D and E.

Using Tree #1, decode the following encoded message: "01000111101". To decode the message, start at the root of the tree and consume digits as you traverse down the tree, stopping when you reach a leaf node. Repeat until all the digits have been processed. Processing the encoded message from left-to-right:

Suppose we were encoding messages that the following probabilities for each of the 5 symbols:

Which of the two encodings above (Tree #1 or Tree #2) would yield the shortest encoded messages averaged over many messages? Using Tree #1, the expected length of the encoding for one symbol is:

1*p(A) + 3*p(B) + 3*p(C) + 3*p(D) + 3*p(E) = 2.0 Using Tree #2, the expected length of the encoding for one symbol is:

2*p(A) + 2*p(B) + 2*p(C) + 3*p(D) + 3*p(E) = 2.25 So using the encoding represented by Tree #1 would yield shorter messages on the average.

Using the probabilities for A, B, C, D and E given above, construct a variable-length binary decoding tree using a simple greedy algorithm as follows:

Begin with the set S of symbols to be encoded as binary strings, together with the probability P(x) for each symbol x. The probabilities sum to 1, and measure the frequencies with which each symbol appears in the input stream. In the example from lecture, the initial set S contains the four symbols and associated probabilities in the above table.
Repeat the following steps until there is only 1 symbol left in S:
1. Choose the two members of S having lowest probabilities. Choose arbitrarily to resolve ties. In the example aove, D and E might be the first nodes chosen.
2. Remove the selected symbols from S, and create a new node of the decoding tree whose children (sub-nodes) are the symbols you've removed. Label the left branch with a "0", and the right branch with a "1". In the first iteration of the example above, the bottom-most internal node (leading to D and E) would be created.
3. Add to S a new symbol (e.g., "DE" in our example) that represents this new node. Assign this new symbol a probability equal to the sum of the probabilities of the two nodes it replaces.

S = {A/0.5 B/0.125 C/0.125 D/0.125 E/0.125}
  arbitrarily choose D & E
  encoding: "0" => D, "1" => E
S = {A/0.5 B/0.125 C/0.125 DE/0.25}
  choose B & C
  encoding: "0" => B, "1" => C
S = {A/0.5 BC/0.25 DE/0.25}
  choose BC & DE
  encoding: "00" => B, "01" => C, "10" => D, "11" => E
S = {A/0.5 BCDE/0.5}
  choose A & BCDE
  encoding: "0" => A, "100" => B, "101" => C, "110" => D, "111" => E
S = {ABCDE/1.0}

This Tree #1 shown in the diagram above. The choice of D & E as the first symbols to combine was arbitrary -- we could have chosen any two symbols from B, C, D and E. So there are many equally plausible encodings that might emerge from this algorithm, corresponding the interchanging B, C, D and E at the leaves of the tree. Huffman coding is used to compactly encode the species of fish tagged by a game warden. If 50% of the fish are bass and the rest are evenly distributed among 15 other species, how many bits would be used to encode the species of a bass? 1 bit, using the algorithm described above. Consider the sum of two six-sided dice. Even when the dice are "fair" the amount information conveyed by a single sum depends on what the sum is since some sums are more likely than others, as shown in the following figure:

What is the average number of bits of information provided by the sum of 2 dice? Suppose we want to transmit the sums resulting from rolling the dice 1000 times. How many bits should we expect that transmission to take? Average number of bits = sum p_ilog₂(1/p_i) for i = 2 through 12. Using the probabilities given in the figure above the average number of bits of information provided by the sum of two dice is 3.2744.

So if we had the perfect encoding, the expected length of the transmission would be 3274.4 bits. If we encode each sum separately we can't quite achieve this lower bound -- see the next question for details. Suppose we want to transmit the sums resulting from rolling the dice 1000 times. If we use 4 bits to encode each sum, we'll need 4000 bits to transmit the result of 1000 rolls. If we use a variable-length binary code which uses shorter sequences to encode more likely sums then the expected number of bits need to encode 1000 sums should be less than 4000. Construct a variable-length encoding for the sum of two dice whose expected number of bits per sum is less than 3.5. (Hint: It's possible to find an encoding for the sum of two dice with an expected number of bits = 3.306.) Using the greedy algorithm given above, we arrive at the following encoding which has 3.3056 as the expected number of bits for each sum.

Okay, so can we make an encoding for transmitting 1000 sums that has an expected length smaller than 3306 bits? Yes, but we have to look at encoding more than one sum at a time, e.g., by applying the construction algorithm to pairs of sums, or ultimately to all 1000 sums at once. Many of the more sophisticated compression algorithms consider sequences of symbols when constructing the appropriate encoding scheme. Variable-length encoding

After spending the afternoon in the dentist's chair, Ben Bitdiddle has invented a new language called DDS made up entirely of vowels (the only sounds he could make with someone's hand in his mouth). The DDS alphabet consists of the five letters "A", "E", "I", "O", and "U" which occur in messages with the following probabilities:

Letter	Probability of occurrence
A	p(A) = 0.15
E	p(E) = 0.4
I	p(I) = 0.15
O	p(O) = 0.15
U	p(U) = 0.15

If you are told that the first letter of a message is "A", give an expression for the number of bits of information have you received. Using the formula given in lecture, the number of bits of information is log₂(1/p(A)) = log₂(1/0.15)

Ben is trying to invent a fixed-length binary encoding for DDS that permits detection and correction of single bit errors. Briefly describe the constraints on Ben's choice of encodings for each letter that will ensure that single-bit error detection and correction is possible. (Hint: think about Hamming distance.) Each encoding must differ from other encodings in at least 3 bit positions, i.e., encodings must have a Hamming distance >= 3. This ensures that each received codeword (even those with single-bit errors) can be associated with a particular source encoding.

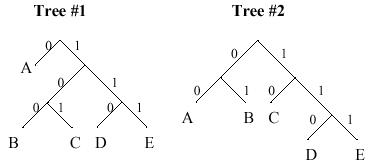
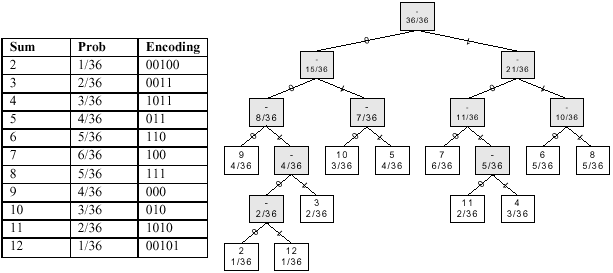
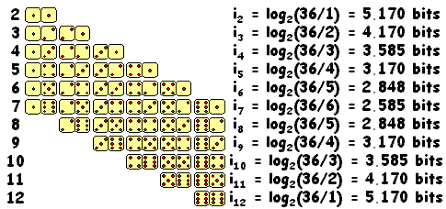Giving up on error detection and correction, Ben turns his attention to transmitting DDS messages using as few bits as possible. Assume that each letter will be separately encoded for transmission. Help him out by creating a variable-length encoding that minimizes the average number of bits transmitted for each letter of the message. Using the simple "greedy" algorithm described above:

S = {A/0.15 E/0.4 I/0.15 O/0.15 U/0.15}
  arbitrarily choose O & U
  encoding: "0" => O, "1" => U
S = {A/0.15 E/0.4 I/0.15 OU/0.3}
  choose A & I
  encoding: "0" => A, "1" => I
S = {AI/0.3 E/0.4 OU/0.3}
  choose AI & OU
  encoding: "00" => A, "01" => I, "10" => O, "11" => U
S = {AIOU/0.6 E/0.4}
  choose E & AIOU
  encoding: "0" => E, "100" => A, "101" => I, "110" => O, "111" => U
S = {AEIOU/1.0}

Note that the assignments of symbols to encodings "0" and "1" were arbitrary and could have been swapped at each level. So, for example, swapping the encoding at the last step would have resulted in

  encoding: "1" => E, "000" => A, "001" => I, "010" => O, "011" => U

which achieves the same average bits/symbol as the previous encoding. Modular arithmetic and 2's complement representation

Most computers choose a particular word length (measured in bits) for representing integers and provide hardware that performs various arithmetic operations on word-size operands. The current generation of processors have word lengths of 32 bits; restricting the size of the operands and the result to a single word means that the arithmetic operations are actually performing arithmetic modulo 2³².

Almost all computers use a 2's complement representation for integers since the 2's complement addition operation is the same for both positive and negative numbers. In 2's complement notation, one negates a number by forming the 1's complement (i.e., for each bit, changing a 0 to 1 and vice versa) representation of the number and then adding 1. By convention, we write 2's complement integers with the most-significant bit (MSB) on the left and the least-significant bit (LSB) on the right. Also by convention, if the MSB is 1, the number is negative; otherwise it's non-negative. How many different values can be encoded in a 32-bit word? Each bit can be either "0" or "1", so there are 2³² possible values which can be encoded in a 32-bit word. Please use a 32-bit 2's complement representation to answer the following questions. What are the representations for

What are the decimal values for the most positive and most negative integers? zero = 0000 0000 0000 0000 0000 0000 0000 0000
most positive integer = 0111 1111 1111 1111 1111 1111 1111 1111 = 2³¹-1
most negative integer = 1000 0000 0000 0000 0000 0000 0000 0000 = -2³¹
Since writing a string of 32 bits gets tedious, it's often convenient to use hexadecimal notation where a single digit in the range 0-9 or A-F is used to represent groups of 4 bits using the following encoding:

	hex bits        hex bits        hex bits        hex bits
	 0  0000         4  0100         8  1000         C  1100
	 1  0001         5  0101         9  1001         D  1101
	 2  0010         6  0110         A  1010         E  1110
	 3  0011         7  0111         B  1011         F  1111

Give the 8-digit hexadecimal equivalent of the following decimal and binary numbers: 37₁₀, -32768₁₀, 11011110101011011011111011101111₂. 37 = 00000025₁₆
-32768 = FFFF8000₁₆
1101 1110 1010 1101 1011 1110 1110 1111₂ = DEADBEEF₁₆

Calculate the following using 6-bit 2's complement arithmetic (which is just a fancy way of saying to do ordinary addition in base 2 keeping only 6 bits of your answer). Show your work using binary (base 2) notation. Remember that subtraction can be performed by negating the second operand and then adding it to the first operand.

Explain what happened in the last addition and in what sense your answer is "right".

  13 = 001101      15 = 001111      27 = 011011
+ 10 = 001010     -18 = 101110     - 6 = 111010
  ===========      ===========      ===========
  23 = 010111      -3 = 111101      21 = 010101

  -6 = 111010      21 = 010101      31 = 011111
 -15 = 110001     -21 = 101011     +12 = 001100
  ===========     ============      ===========
 -21 = 101011       0 = 000000     -21 = 101011 (!)

In the last addition, 31 + 12 = 43 exceeds the maximum representable positive integer in 6-bit two's complement arithmetic (max int = 2⁵-1 = 31). The addition caused the most significant bit to become 1, resulting in an "overflow" where the sign of the result differs from the signs of the operands. At first blush "Complement and add 1" doesn't seem to an obvious way to negate a two's complement number. By manipulating the expression A+(-A)=0, show that "complement and add 1" does produce the correct representation for the negative of a two's complement number. Hint: express 0 as (-1+1) and rearrange terms to get -A on one side and XXX+1 on the other and then think about how the expression XXX is related to A using only logical operations (AND, OR, NOT). Start by expressing zero as (-1 + 1):

A + (-A) = -1 + 1 Rearranging terms we get:

(-A) = (-1 - A) + 1 The two's complement representation for -1 is all ones, so looking at (-1 - A) bit-by-bit we see:

   1   ...  1   1
-  A_N-1 ...  A₁  A₀
  ===============
  ~A_N-1 ... ~A₁ ~A₀

where "~" is the bit-wise complement operator. We've used regular subtraction rules (1 - 0 = 1, 1 - 1 = 0) and noticed that 1 - A_i = ~A_i. So, finally:

(-A) = ~A + 1 Error detection and correction To protect stored or transmitted information one can add check bits to the data to facilitate error detection and correction. One scheme for detecting single-bit errors is to add a parity bit:

₀

₁

₂

_N-1

When using even parity, p is chosen so that the number of "1" bits in the protected field (including the p bit itself) is even; when using odd parity, p is chosen so that the number of "1" bits is odd. In the remainder of this problem assume that even parity is used.

To check parity-protected information to see if an error has occurred, simply compute the parity of information (including the parity bit) and see if the result is correct. For example, if even parity was used to compute the parity bit, you would check if the number of "1" bits was even.

If an error changes one of the bits in the parity-protected information (including the parity bit itself), the parity will be wrong, i.e., the number of "1" bits will be odd instead of even. Which of the following parity-protected bit strings has a detectable error?

(1) 11101101111011011 (2) 11011110101011011 (3) 10111110111011110 (4) 00000000000000000

Strings 1 and 3 have detectable errors. Note that parity allows one to detect single-bit errors (actually any odd number of errors) but doesn't defend against an even number of bit errors. Detecting errors is useful, but it would also be nice to correct them! To build an error correcting code (ECC) we'll use additional check bits to help pinpoint where the error occurred. There are many such codes; a particularly simple one for detecting and correcting single-bit errors arranges the data into rows and columns and then adds (even) parity bits for each row and column. The following arrangement protects nine data bits:

b0,0	b0,1	b0,2	prow0
b1,0	b1,1	b1,2	prow1
b2,0	b2,1	b2,2	prow2
pcol0	pcol1	pcol2

A single-bit error in one of the data bits (b_I,J) will generate two parity errors, one in row I and one in column J. A single-bit error in one of the parity bits will generate just a single parity error for the corresponding row or column. So after computing the parity of each row and column, if both a row and a column parity error are detected, inverting the listed value for the appropriate data bit will produce the corrected data. If only a single parity error is detected, the data is correct (the error was one of the parity bits).

Give the correct data for each of the following data blocks protected with the row/column ECC shown above.

(1)  1011    (2) 1100    (3) 000    (4) 0111
     0110        0000        111        1001
     0011        0101        10         0110
     011         100                    100

(1)  0011    (2) 1100    (3) 000    (4) 0110
     0110        0000        101        1001
     0011        0101        10         0110
     011         100                    100

(1) and (3) had single bit errors, (2) had no detectable errors, and (4) had an error in a parity bit. The red digits represent corrected values. The row/column ECC can also detect many double-bit errors (i.e., two of the data or check bits have been changed). Characterize the sort of double-bit errors the code does not detect. If parity bits detect an error for exactly one column and exactly one row, this will be interpreted as a single bit error in the corresponding data position. This can happen with two parity bit errors, one in each of the row and column check bits. The fact that two errors occurred is not detected; worse, the corresponding data position is changed from the correct value to the incorrect value. In the days of punch cards, decimal digits were represented with a special encoding called 2-out-of-5 code. As the name implies two out of five positions were filled with 1's as shown in the table below:

Code	Decimal
11000	1
10100	2
01100	3
10010	4
01010	5
00110	6
10001	7
01001	8
00101	9
00011	0

What is the smallest Hamming distance between any two encodings in 2-out-of-5 code? The Hamming distance between any two encodings is the number of bit positions in which the encodings differs. With this code, the smallest Hamming distance is 2. Characterize the types of errors (eg, 1- and 2-bit errors) that can be reliably detected in a 2-out-of-5 code? Codes with a Hamming distance of 2 can detect 1-bit errors. The 2-out-of-5 code also detects 3-bit errors, but not 2-bit errors. Normally when we say a code detects n-bit errors we imply that it detects m-bit errors for m < n. Following this convention, we would say that the 2-out-of-5 code detects 1-bit errors. We know that even parity is another scheme for detecting errors. If we change from a 2-out-of-5 code to a 5-bit code that includes an even parity bit, how many additional data encodings become available? There are 16 possible values for the 4 data bits in the 5-bit parity encoding, six more than the 10 possible values in the 2-out-of-5 code. Hamming single-error-correcting-code

The Hamming single-error-correcting code requires approximately log2(N) check bits to correct single-bit errors. Start by renumbering the data bits with indices that aren't powers of two:

Indices for 16 data bits = 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21

The idea is to compute the check bits choosing subsets of the data in such a way that a single-bit error will produce a set of parity errors that uniquely indicate the index of the faulty bit:

Note that each data bit appears in at least two of the parity calculations, so a single-bit error in a data bit will produce at least two parity errors. When checking a protected data field, if the number of parity errors is zero or one, the data bits are okay (exactly one parity error indicates that one of the parity bits was corrupted). If two or more parity errors are detected then the errors identify exactly which bit was corrupted. What is the relationship between the index of a particular data bit and the check subsets in which it appears? Hint: consider the binary representation of the index. Digit i in the binary expansion of a data bit index indicates whether the index should be included in the calculation of pi. For example, the first data bit (which has index 3 = 00011) would be used in the parity calculation for parity bits p0 and p1. Likewise, the sixth data bit (which has index 10 = 01010) would be used in the parity calculation for parity bits p1 and p3. Since no data bit is assigned an index which is a power of two, we guarantee that each data bit is used in the calculation of at least two different parity bits. If the parity calculations involving p0, p2 and p3 fail, assuming a single-bit error what is the index of the faulty data bit? We need to find the data index that appears in the calculation p0, p2 and p3 but not in the calculations for p1 and p4. Indicies 13 and 15 appear in p0, p2 and p3, but index 15 appears in the calculation for p1. So the index of the data bit that failed is 13.

We can construct the index of the failing data bit directly from the parity calculations using ei = 1 if the pi failed and ei = 0 if it didn't. So if p0, p2 and p3 failed, and the others didn't, the index is e4e3e2e1e0 = 01101 = 13₁₀. The Hamming SECC doesn't detect all double-bit errors. Characterize the types of double-bit errors that will not be detected. Suggest a simple addition to the Hamming SECC that allows detection of all double-bit errors. If errors occur in two separate parity bits, this will be misinterpreted as a single data bit error. Also when certain pairs of data bits have errors, the double-bit error masquerades as a single-bit error in another, unrelated bit (e.g., suppose bits with indicies 19 and 21 both have errors).

We can detect these situations by adding an additional parity bit, p5, which is the parity of all other parity and data bits. If a single data bit failed, this bit would indicate and error. But if exactly two bits have failed, p5 would indicate no error, but p0, p1, ..., p4 would indicate the presence of some error (although the indication might point at the wrong data bit). So, if by looking at p0, p1, ..., p4 it seems as though an error occurred, we should check p5 to make sure that only one error occurred. If p5 does not indicate an error, then a double-bit error occurred.