 Explain what Beta assembly language instruction(s) are needed
to load the value of a variable that has been allocated in the first
32k bytes of main memory (i.e., at an address less than 0x8000).
How would your answer change if the variable was located at address
outside this range (e.g., at address 0x12468).
Explain what Beta assembly language instruction(s) are needed
to load the value of a variable that has been allocated in the first
32k bytes of main memory (i.e., at an address less than 0x8000).
How would your answer change if the variable was located at address
outside this range (e.g., at address 0x12468).
vaddr: LONG(0x12468) ... LDR(vaddr,R0) ; load address of variable into R0 LD(R0,0,R0) ; load Mem[address] into R0
 a = b + 3*c;
a = b + 3*c;
LD(c,R1) SHLC(R1,1,R0) ; 2*c ADD(R0,R1,R0) ; + c LD(b,R1) ADD(R1,R0,R0) ST(R0,a)
 if (a > b) c = 17;
if (a > b) c = 17;
LD(a,R0) LD(b,R1) CMPLE(R0,R1,R0) BT(R0,_L2) CMOVE(17,R0) ST(R0,c) _L2:
LD(sxt_short,R0) BEQ(R0,_L3) LD(b,R1) SHLC(R1,16,R0) ; shift so that bit 15 is now bit 31 SRAC(R0,16,R0) ; shift back, replicating sign bit ST(R0,b)
Assume that the salary component of the structure pointed to by cjt has a byte offset of 8 from the beginning of the structure.
LD(cjt,R1) LD(R1,8,R0) ADDC(R0,3752,R0) ST(R0,8,R1)
LD(i,R0) SHLC(R0,2,R0) LD(R0,a-4,R1) ST(R1,a,R0)
 sum = 0;
sum = 0;for (i = 0; i < 10; i = i+1) sum += i;
ST(R31,sum) ST(R31,i) _L7: LD(sum,R0) LD(i,R1) ADD(R0,R1,R0) ST(R0,sum) ADDC(R1,1,R1) ST(R1,i) CMPLTC(R1,10,R0) BT(R0,_L7)
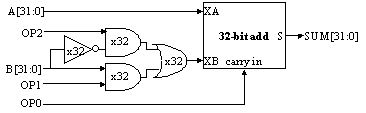 What would be the correct values for OP[2:0] in order to perform a
subtract (i.e., SUM = A - B)?
What would be the correct values for OP[2:0] in order to perform a
subtract (i.e., SUM = A - B)?