Nickles proposes that a new synchronization mechanism, the gerbiphore,
be defined to handle the management of Gerbitrail tubes. His proposal
involves the implementation of a gerbiphore as a C data structure, and
the allocation of a single gerbiphore to each tube in a Gerbitrail
cage configuration.
Nickles's proposed implementation is:
semaphore mutex=1;
struct gerbiphore { /* definition of "gerbiphore" structure*/
int dir; /* Direction: 0 means unspecified. */
int count; /* Number of Gerbils in tube */
} A, B, ...; /* one gerbiphore for each tube */
int Fwd=1, Bkwd=2; /* Direction codes for tube travel */
/* genter(g, dir) called with gerbiphore pointer g and direction dir
whenever a gerbil wants to enter the tube attached to g
in direction dir */
genter(struct gerbiphore *g, int dir) {
loop:
wait(mutex);
if (g->dir == 0)
g->dir = dir; /* If g->dir unassigned, grab it! */
if (g->dir == dir) {
g->count = 1 + g->count; /* One more gerbil in tube. */
*********; /* MISSING LINE! */
return;
}
signal(mutex);
goto loop;
}
/* gleave(g, dir) is called whenever a gerbil leaves the tube
attached to gerbiphore g in direction dir. */
gleave(struct gerbiphore *g, int dir) {
wait(mutex);
g->count = g->count - 1;
if (g->count == 0) g->dir = 0;
signal(mutex);
}
Unfortunately a blotch of red wine obscures one line of Nickles's
code. The team of stain analysts hired to decode the blotch eventually
respond with a sizable bill and the report that "it appears to be
Ch. Petrus, 1981". Again, your services are needed.
What belongs in place of ********* at the line commented
"MISSING LINE"?
signal(mutex). We have to release the mutual exclusion lock before
returning from genter.
 Assuming execution is eventually halted, how many C's are printed
when the set of processes runs?
Assuming execution is eventually halted, how many C's are printed
when the set of processes runs?
 Assuming execution is eventually halted, how many D's are
printed when this set of processes runs?
Assuming execution is eventually halted, how many D's are
printed when this set of processes runs?
 What is the smallest number of A's that might be printed when
this set of processes runs?
What is the smallest number of A's that might be printed when
this set of processes runs?
 Is CABABDDCABCABD a possible output sequence when this set of
processes runs?
Is CABABDDCABCABD a possible output sequence when this set of
processes runs?
 Is CABACDBCABDD a possible output sequence when this set of
processes runs?
Is CABACDBCABDD a possible output sequence when this set of
processes runs?
 Is it possible for execution to be halted with either U or V
having a non-zero value?
Is it possible for execution to be halted with either U or V
having a non-zero value?
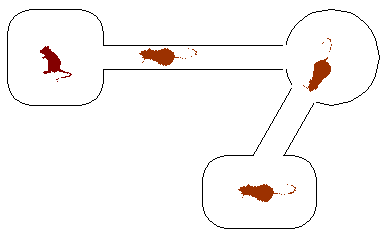 The Gerbitrail cages are immensely successful, except for one tragic
flaw: the dreaded GERBILOCK. Gerbilock is a situation that arises
when multiple gerbils enter a tube going in opposite directions,
meeting within the tube as shown below:
The Gerbitrail cages are immensely successful, except for one tragic
flaw: the dreaded GERBILOCK. Gerbilock is a situation that arises
when multiple gerbils enter a tube going in opposite directions,
meeting within the tube as shown below:
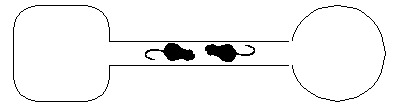 Since each gerbil is determined to move forward and there is
insufficient room to pass, both gerbils remain gerbilocked forever.
There is, however, hope on the horizon. Gerbitrail has developed
little mechanical ggates that can be placed at the ends of each tube,
and which can both sense and lock out gerbil crossings. All ggates are
controlled by a single computer. Each ggate X has two routines,
X_Enter and X_Leave, which are called when a gerbil tries to enter or
leave respectively the tube via that ggate; the gerbil is not allowed
to procede (ie, to enter or leave) until the Enter or Leave call
returns. Gerbitrail engi- neers speculate that these routines can
solve Gerbilock using semaphores.
They perform the following experiment:
Since each gerbil is determined to move forward and there is
insufficient room to pass, both gerbils remain gerbilocked forever.
There is, however, hope on the horizon. Gerbitrail has developed
little mechanical ggates that can be placed at the ends of each tube,
and which can both sense and lock out gerbil crossings. All ggates are
controlled by a single computer. Each ggate X has two routines,
X_Enter and X_Leave, which are called when a gerbil tries to enter or
leave respectively the tube via that ggate; the gerbil is not allowed
to procede (ie, to enter or leave) until the Enter or Leave call
returns. Gerbitrail engi- neers speculate that these routines can
solve Gerbilock using semaphores.
They perform the following experiment:
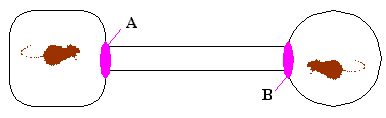 where each of the ggates A and B are controlled by the following code:
where each of the ggates A and B are controlled by the following code: