Problem 1. Modular arithmetic and 2's complement representation

Most computers choose a particular word length (measured in bits) for representing integers and provide hardware that performs various arithmetic operations on word-size operands. The current generation of processors have word lengths of 32 bits; restricting the size of the operands and the result to a single word means that the arithmetic operations are actually performing arithmetic modulo 2³².

Almost all computers use a 2's complement representation for integers since the 2's complement addition operation is the same for both positive and negative numbers. In 2's complement notation, one negates a number by forming the 1's complement (i.e., for each bit, changing a 0 to 1 and vice versa) representation of the number and then adding 1. By convention, we write 2's complement integers with the most-significant bit (MSB) on the left and the least-significant bit (LSB) on the right. Also by convention, if the MSB is 1, the number is negative; otherwise it's non-negative.

How many different values can be encoded in a 32-bit word?

Each bit can be either "0" or "1", so there are 2³² possible values which can be encoded in a 32-bit word.

Please use a 32-bit 2's complement representation to answer the following questions. What are the representations for
What are the decimal values for the most positive and most negative integers?

zero = 0000 0000 0000 0000 0000 0000 0000 0000
most positive integer = 0111 1111 1111 1111 1111 1111 1111 1111 = 2³¹-1
most negative integer = 1000 0000 0000 0000 0000 0000 0000 0000 = -2³¹

Since writing a string of 32 bits gets tedious, it's often convenient to use hexadecimal notation where a single digit in the range 0-9 or A-F is used to represent groups of 4 bits using the following encoding:
```
	hex bits        hex bits        hex bits        hex bits
	 0  0000         4  0100         8  1000         C  1100
	 1  0001         5  0101         9  1001         D  1101
	 2  0010         6  0110         A  1010         E  1110
	 3  0011         7  0111         B  1011         F  1111
```
Give the 8-digit hexadecimal equivalent of the following decimal and binary numbers: 37₁₀, -32768₁₀, 11011110101011011011111011101111₂.

37 = 00000025₁₆
-32768 = FFFF8000₁₆
1101 1110 1010 1101 1011 1110 1110 1111₂ = DEADBEEF₁₆

Calculate the following using 6-bit 2's complement arithmetic (which is just a fancy way of saying to do ordinary addition in base 2 keeping only 6 bits of your answer). Show your work using binary (base 2) notation. Remember that subtraction can be performed by negating the second operand and then adding it to the first operand.
```
	13 + 10  
	15 - 18
	27 - 6
	-6 - 15
	21 + (-21)
	31 + 12
```
Explain what happened in the last addition and in what sense your answer is "right".
```
  13 = 001101      15 = 001111      27 = 011011
+ 10 = 001010     -18 = 101110     - 6 = 111010
  ===========      ===========      ===========
  23 = 010111      -3 = 111101      21 = 010101

  -6 = 111010      21 = 010101      31 = 011111
 -15 = 110001     -21 = 101011     +12 = 001100
  ===========     ============      ===========
 -21 = 101011       0 = 000000     -21 = 101011 (!)
```
In the last addition, 31 + 12 = 43 exceeds the maximum representable positive integer in 6-bit two's complement arithmetic (max int = 2⁵-1 = 31). The addition caused the most significant bit to become 1, resulting in an "overflow" where the sign of the result differs from the signs of the operands.

At first blush "Complement and add 1" doesn't seem to an obvious way to negate a two's complement number. By manipulating the expression A+(-A)=0, show that "complement and add 1" does produce the correct representation for the negative of a two's complement number. Hint: express 0 as (-1+1) and rearrange terms to get -A on one side and XXX+1 on the other and then think about how the expression XXX is related to A using only logical operations (AND, OR, NOT).
Start by expressing zero as (-1 + 1):
Rearranging terms we get:
The two's complement representation for -1 is all ones, so looking at (-1 - A) bit-by-bit we see:
```
   1   ...  1   1
-  A_N-1 ...  A₁  A₀
  ===============
  ~A_N-1 ... ~A₁ ~A₀
```
where "~" is the bit-wise complement operator. We've used regular subtraction rules (1 - 0 = 1, 1 - 1 = 0) and noticed that 1 - A_i = ~A_i. So, finally:

Problem 2. Recall that in a N-bit sign-magnitude representation, the most significant bit is the sign (0 for positive, 1 for negative) and the remaining N-1 bits are the magnitude.

What range of numbers can be represented with an N-bit sign-magnitude number? With an N-bit two's-complement number?

For sign-magnitude the range is -(2^N-1-1) to (2^N-1-1).
For two's complement the range is -2^N-1 to (2^N-1-1).

Create a Verilog module that converts an N-bit sign-magnitude input into an N-bit two's complement output.

Problem 3. Carry-select adder

In thinking about the propagation delay of a ripple-carry adder, we see that the higher-order bits are "waiting" for their carry-ins to propagate up from the lower-order bits. Suppose we split off the high-order bits and create two separate adders: one assuming that the carry-in was 0 and the other assuming the carry-in was 1. Then when the correct carry-in was available from the low-order bits, it could be used to select which high-order sum to use. The diagram below shows this strategy applied to an 8-bit adder: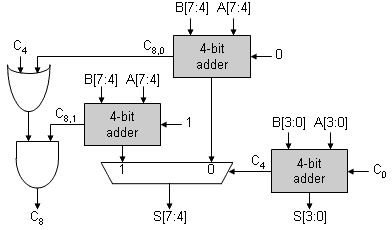

Compare the latency of the 8-bit carry-select adder show above to a regular 8-bit ripple-carry adder.

For the low-order 4 bits, the latency is the same for both implementations: T_{PD,4-BIT ADDER}. But with the carry-select adder, the remaining latency is the propagation delay of the 4-bit 2:1 multiplexer (T_{PD,2:1 MUX}) instead of the longer time it takes for the carry to ripple through another 4 bits of adder (T_{PD,4-BIT ADDER}). If we consider an N-bit adder, the latencies are:
T_{PD,N-BIT RIPPLE} = 2 * T_{PD,(N/2)-BIT RIPPLE}
T_{PD,N-BIT CARRY-SELECT} = T_{PD,(N/2)-BIT RIPPLE} + T_{PD,2:1 MUX}
As N gets large the carry-select adder is almost twice as fast as a ripple-carry adder since the delay through the 2:1 mux is independent of N. The carry-select strategy can be applied recursively to the (N/2)-bit ripple-carry adder, and so on, ultimately producing an adder with O(log₂N) latency.

The logic shown for C₈ seems a bit odd. One might have expected C₈ = C_8,0 + (C₄*C_8,1). Explain why both implementations are equivalent and suggest why the logic shown above might be prefered. Hint: What can we say about C_8,1 when C_8,0=1?
If we think about carry generation, it's easy to see that if C_8,0=1 then C_8,1=1, i.e., if we get a carry with C_IN=0, we'll also get a carry when C_IN=1. Using this fact we can do a little Boolean algebra:
```
C8 = C8,0 + (C4 * C8,1)
                  ____
   = C8,0*(C8,1 + C8,1) + (C4 * C8,1)
                             ____
   = (C8,0 * C8,1) + (C8,0 * C8,1) + (C4 * C8,1)
   = (C8,0 * C8,1) + 0 + (C4 * C8,1)
   = (C8,0 + C4)*C8,1
```
In the worst case (the carry-in rippling all the way up), C_8,1 will take a little longer to compute than C_8,0, so the logic for C₈ shown in the diagram will be a little faster since it provides the shorter path to C₈.

Problem 4. Pipelining.

Pipelining is particular form of retiming where the goal is to increase the throughput (number of results per second) of a circuit. Consider the circuit diagram below; the solid rectangles represent registers, the square are blocks of combinational logic:

Each combinational block in the diagram is annotated with it's propagation delay in ns. For this problem assume that the registers are "ideal", i.e., they have zero propagation delay, and zero setup and hold times.

What are the latency and throughput of the circuit above? Latency is how long it takes for a value in the input register to be processed and the result appear at the output register. Throughput is the number of results per second.

The register-to-register T_PD is the T_PD of the longest path (timewise) through the combinational logic = 53ns. A value in the input register is processed in one clock cycle (latency = 53ns), and the circuit can produce an output every cycle (throughput = 1 answer/53ns).

Pipeline the circuit above for maximum throughput. Pipelining adds additional registers to a circuit; we'll do this by adding additional registers at the output and then use the retiming transformation to move them between the combinational blocks. What are the latency and throughput of your resulting circuit?

To maximize the throughput, we need to get the "30" block into it's own pipeline stage. So we'll draw the retiming contours like so:

Note there is an alternative way we could have drawn the contours to reach the goal of isolating the "30" block; it might be that other implementation considerations would help pick which alternative was more attracive. Similarly, we could have instead added registers at the input and used retiming to move them into the circuit.
The contours above lead to the following piplelined circuit diagram:

A good check to see if the retiming is correct is to verify that there are the same number of registers on every path from the input(s) to the output(s).
The register-to-register T_PD is now 30ns, so the throughput of the piplined circuit is 1/30ns. The latency has increased to 3 clock cycles, or 90ns. In general increasing the throughput through pipelining always leads to an increase in latency. Fortunately latency is not an issue for many digital processing circuits -- eg, microprocessors -- where we care more about how many results we get per second much more than how long it takes to process an individual result.

Arithmetic Circuits and Behavioral Transformations