Logic Gates

Problem 1. The following diagram shows a schematic for the pulldown circuitry for a particular CMOS gate:

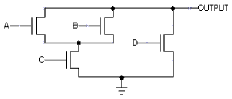
  1. What is the correct schematic for the pullup circuitry?
  1. Assuming the pullup circuitry is designed correctly, what is the logic function implemented this gate?
  1. Assuming the pullup circuitry is designed correctly, when the output of the CMOS gate above is a logic "0", in the steady state what would we expect the voltage of the output terminal to be? What would be the voltage if the output were a logic "1"?

Problem 2. The following diagram shows a schematic for the pullup circuitry for a particular CMOS gate:

  1. Draw a schematic for the pulldown circuitry for this CMOS gate.
  1. Assuming the pulldown circuitry is designed correctly, give an expression for the logic function implemented by this gate.

Problem 3. Consider the following circuit built from nfets and pfets:

  1. Can this circuit be used as a CMOS gate? If not, explain why. If so, what function does it compute?

Problem 4. Consider the 4-input Boolean function Y = (A*B) + (C*D) where "*" is AND and "+" is OR.

  1. Implement the function with a single 4-input CMOS gate and an inverter.

Problem 5. Anna Logue, a circuit designer who missed several early 6.111 lectures, is struggling to design her first CMOS logic gate. She has implemented the following circuit:

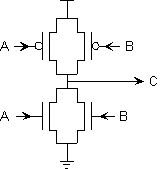
Anna has fabricated 100 test chips containing this circuit, and has a simple testing circuit which allows her to try out her proposed gate statically for various combinations of the A and B inputs. She has burned out 97 of her chips, and needs your help before destroying the remaining three. She is certain she is applying only valid input voltages, and expects to find a valid output at terminal C. Anna also keeps noticing a very faint smell of smoke.
  1. What is burning out Anna's test chips? Give a specific scenario, including input values together with a description of the failure scenario. For what input combinations will this failure occur?
  1. Are there input combinations for which Anna can expect a valid output at C? Explain.
  1. One of Anna's test chips has failed by burning out the pullup connected to A as well as the pulldown connected to B. Each of the burned out FETs appears as an open circuit, but the rest of the circuit remains functional. Can the resulting circuit be used as a combinational device whose two inputs are A and B? Explain its behavior for each combination of valid inputs.
  1. In order to salvage her remaining three chips, Anna connects the A and B inputs of each and tries to use it as a single-input gate. Can the result be used as a single-input combinational device? Explain.

Problem 6. Occasionally you will come across a CMOS circuit where the complementary nature of the n-channel pull-downs and p-channel pull-ups are not obvious, as in the circuit shown below:

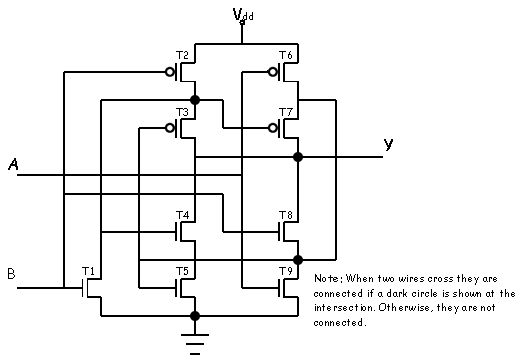
  1. Construct a table that gives the on-off status of each transistor in the circuit above for all combinations of inputs A and B.
  1. Compute the output, Y, for each input combination and describe the function of the above circuit.

Problem 7. Consider the following circuit that implements the 2-input function H(A,B):

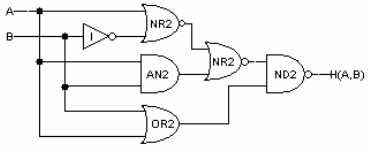
  1. Fill in the following truth table for H:

    ABH
    00 
    01 
    10 
    11 
  1. Give a sum-of-products expression that corresponds to the truth table above.
  1. Using the following table of timing specifications for each component, what are tCD and tPD for the circuit shown above?

    gatetCDtPD
    I3ps15ps
    ND25ps30ps
    AN212ps50ps
    NR25ps30ps
    OR212ps50ps

Problem 8. Gates and Boolean equations

  1. Show the Boolean equation for the function F described by the following circuit:

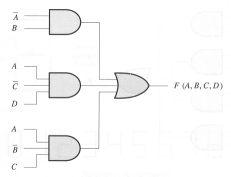
  1. Consider the circuit shown below. Each of the control inputs, C0 through C3, must be tied to a constant, either 0 or 1.

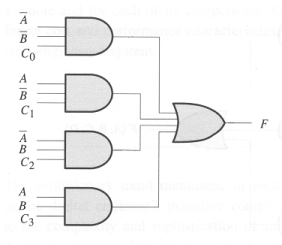    What are the values of C0 through C3 that would cause F to be the exclusive OR of A and B?

  1. Can any arbitrary Boolean function of A and B be realized through appropriate wiring of the control signals C0 through C3?
  1. Give a sum-of-products expression for each of the following circuits:

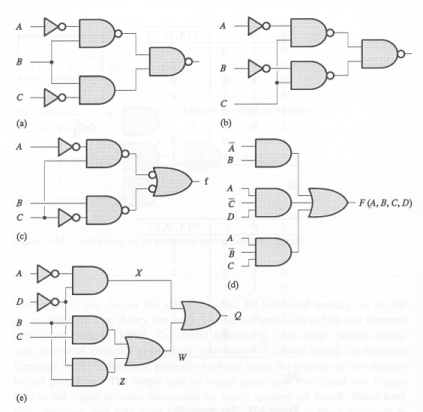
  1. Give a canonical sum-of-products expression for the Boolean function described by each truth table below

  1. We've seen that there are a total of sixteen 2-input Boolean functions. How many 5-input Boolean functions are there?

Problem 9. A priority encoder has inputs that are assigned some predetermined order. The output is the binary encoding of the first "1" valued input from the ordered list, and it is zero otherwise.

  1. Give the truth table for a 3-input priority encoder.
  1. Give a sum of products realization of this priority encoder.

Problem 10. Suppose we are building circuits using only the following three components:

Consider the following circuit constructed from an inverter and four 2-input NOR gates:

  1. What is tPD for this circuit?
  1. What is tCD for this circuit?
  1. What is tPD of the fastest equivalent circuit (i.e., one that implements the same function) built using only the three components listed above?

Problem 11. Suppose that each component in the circuit below has a propagation delay (tpd) of 10ns, a contamination delay (tcd) of 1ns, and negligable rise and fall times. Suppose initially that all four inputs are 1 for a long time and then the input D changes to 0.

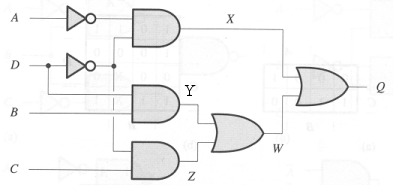
  1. Draw a waveform plot showing how X, Y, Z, W and Q change with time after the input transition on D.