Synthesis of combinational logic
Problem 1.
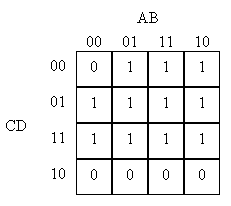
A certain function F has the following truth table:
A B C | F
========|===
0 0 0 | 1
0 0 1 | 0
0 1 0 | 0
0 1 1 | 1
1 0 0 | 1
1 0 1 | 1
1 1 0 | 0
1 1 1 | 1
-
Write a sum-of-products expression for F.
-
Write a minimal sum-of-products expression for F.
Show a combinational circuit that implements F using only
INV and NAND gates.
-
Implement F using one 4-input MUX and inverter.
-
Write a minimal sum-of-products expression for NOT(F).
Problem 2.
-
Give a minimal sum-of-products expression that is equivalent
to the follow logic expressions:
_____
(A) A + B
_ _ _ _ _ _ _
(B) A*B*C + A*B*C + A*B*C + A*B*C + A*B*C + A*B*C
-
Multiple choice:
A Karnaugh map can't represent more than 2 variables along a single
dimension because
- Gray code counts can't go beyond 2 bits.
- Each value v along a dimension must be adjacent to all values that are
Hamming distance 1 from v.
- Three is not a power of two.
- No reason.
You can represent 3 variables along a dimension. You couldn't make
5-variable K-maps otherwise.
-
What is the maximum number of product terms in a minimal
sum-of-products expressions with three variables?
-
True or false: A boolean function of N variables with greater than
2N-1 product terms can always be simplified to an
expression using fewer product terms.
-
Suppose the stock room is very low on components and
has only five NAND gates on hand. Would we be able to
build an implementation of any arbitary 2-input boolean
function?
Problem 3.
In the Karnaugh maps below the use of "X" in a cell
indicates a "don't care" situation where the value of the function for those
inputs can be chosen to minimize the size of the overall expression.
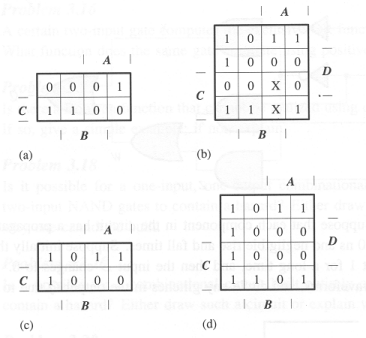
-
Circle the prime implicants in the Karnaugh maps and write a minimal
sum-of-products expression for each of the maps.
Problem 4.
The following diagram shows the pulldown circuitry for a static CMOS
logic gate that implements the function F(A,B,C,D):
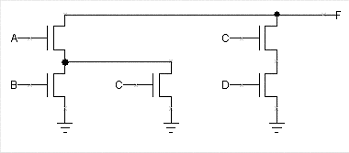
-
Draw a circuit diagram for the pullup circuitry that would complete
the static CMOS implementation of F(A,B,C,D).
-
Assuming the correct pullup circuitry is added to the diagram above,
give a minimal sum-of-products expression for F(A,B,C,D).
Problem 5.
A certain 3-input function G(A,B,C) has the following implementation:
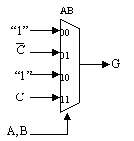
-
Give a minimal sum-of-products expression for G.
Problem 6.
(Katz, problem 4.9) Implement the 2-bit adder function (i.e., 2-bit
binary number AB plus 2-bit binary number CD yields a 3-bit result
XYZ) using three 8:1 multiplexers.
-
Give the truth tables for X, Y and Z.
-
Show how to implement X, Y, Z using three 8:1 multiplexers. You can
assume you have the constants 0 and 1, the inputs and their complements
available in addition to the multiplexers. Explain how you derived
the inputs to multiplexers.
Problem 7.
(Katz, problem 4.11) You are working for a company that produces clones
of famous name computers. Your assign is to copy the circuit shown below,
which is a component of the computer. Because of copyright laws, your boss
is very emphatic that the new circuit not resemble the old one. Also,
your boss' brother-in-law's electronics wholesale firm has a special
deal on multiplexers. So the boss wants you to use only 4:1 multiplexers
in your circuit.
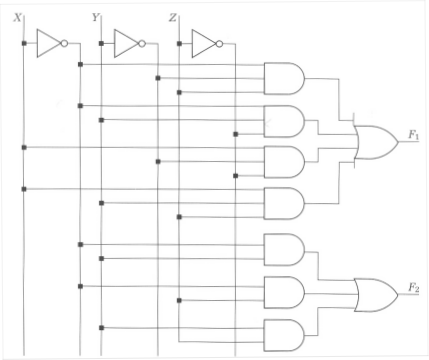
-
Construct a truth table for the circuit above.
-
Design an implementation using only 4:1 multiplexers, the constants
0 and 1, and the inputs.
Problem 8.
(Katz, problem 4.15a) Consider the following function in sum of products
form (not necessarily minimized):
_
F(A,B,C,D) = ABC + AD + AC
-
Implement the function F using only an 8:1 multiplexer. You can assume
that you have the constants 0 and 1, and the inputs, but you don't have
their complements (nor inverters to create them!).
Problem 9.
(Katz, problem 4.22) You are to implement a combinational multiplier. It
has two 2-bit inputs and a 4-bit output. The first 2-bit input is represented
by the variables A, B; the second 2-bit input is represented by C, D. The outputs
are W, X, Y, Z, from the most significant bit to the least.
-
Complete a truth table that describes the functional behavior of the multiplier.
-
Find the minimum sum of products forms for the outputs using Karnaugh maps.
Problem 10.
(Katz, problem 4.23)
An n-input majority fnction asserts its output whenever more than half
of its inputs are asserted. You are to implement a seven-input majority
function, which will assert its output whnever four or more of its inputs
are asserted.
Don't panic just because this is a seven-variable function. Build it
up as multilevel function whose subfunctions each have less than six
variables. As a block diagram, it looks like the figure below. Circuits #1
and #2 tally the number of the inputs that are asserted, providing the count
in binaryon the outputs (V,Y are the most significant bits; W,Z are the least
significant bits). Based on these second-level inputs, Q determines if
more than four or more of the original inputs are 1.
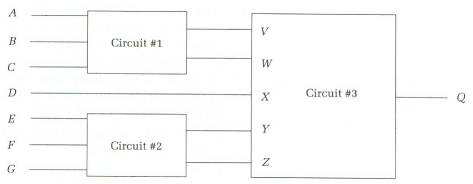
-
Find the minimized sum of products for circuit #1 (circuit #2 is
identical). The functions V and W should look familiar. What do
they implement?
-
Complete the 5-variable truth table for circuit #3.
-
Find the minimum sum of products form for Q using
the Karnaugh map method. Hint: extend a 4-variable
Karnaugh map into the third dimension.
Problem 11.
Digital Widgets Co. has introduced a new logic IC consisting of two
comparator cells in a 14-pin package. A comparator cell, as drawn
below, has four inputs and two outputs.
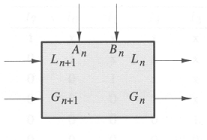
The inputs are labeled An, Bn, Gn+1, and Ln+1, and the outputs are
labeled Gn and Ln. The G and L signals have the meanings "A greater
than B" and "A less than B," respectively. If both G and L are false,
the meaning is A = B. G and L are never both true. Two k-bit numbers
A and B may be compared using a circuit such as the following:
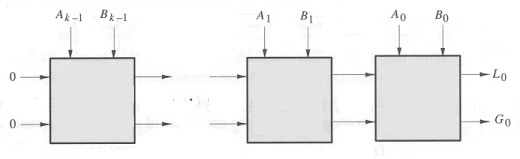
The most significant bits are supplied as Ak-1 and
Bk-1, and the least significant bits are A0 and B0.
The output of a comparison is taken from the G and L outputs of the
lowest-order cell (G0 and L0). Gn+1 and Ln+1 of the highest-order
cell are connected to logical 0 to indicate that the numbers are
assumed to be equal until some difference is found between a pair of
bits Ai and Bi.
If the Gn+1 and Ln+1 inputs indicate that higher-order bits have
established A > B or A < B, then cell n must propagate that
result to Gn and Ln. However, if Gn+1 and Ln+1 indicate that the
higher-order bits are equal, then cell n must compare its bit of A and
B to determine if A > B, A < B, or A = B and must signal that
result appropriately at Gn and Ln.
-
Draw a logic diagram for an implementation of the Digital Widgets
comparator cell.
-
Since there is delay associated with the propagation of the G and L
signals through each cell, we could make the comparator work faster
by redesigning the basic cell to compare two bits at a time, halving the number
of stages through which the G and L signals will need to propagate.
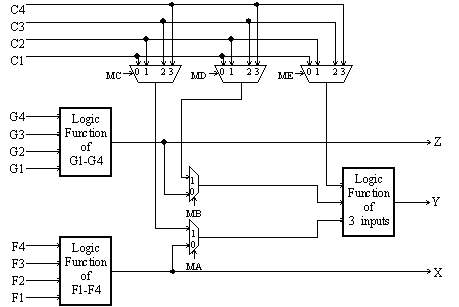
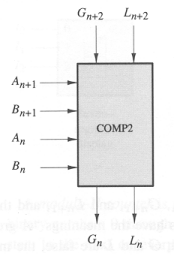 Work out expressions for Gn and Ln as functions of Gn+2, Ln+2,
An+1, Bn+1, An, and Bn. Express your answers in the form
Work out expressions for Gn and Ln as functions of Gn+2, Ln+2,
An+1, Bn+1, An, and Bn. Express your answers in the form
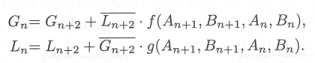
-
Given a reasonable implementation of the equations for Gn and Ln
derived in part B, how does the delay from a change in Gn+2
and Ln+2 to the appearance of correct outputs at Gn
and Ln compare with the corresponding delay for a circuit composed
of a cascade of two of the cells developed in part A?
Assume that all A and B inputs remain unchanged throughout.
Note: The reason for our interest in the propagation delay of the G and
L signals, specifically, is that in a chain of N comparators, every
extra gate delay in the G--L path will penalize total performance by N
gate delays. The time it takes for a change in an A or B input to be reflected
in the corresponding G or L output is also important, but improvements here
can at best result in decreasing total delay by some constant amount.
Problem 12.
The Xilinx 4000 series field-programmable gate array (FPGA) can be
programmed to emulate a circuit made up of many thousands of gates;
for example, the XC4025E can emulate circuits with up to 25,000 gates.
The heart of the FPGA architecture is a configurable logic block (CLB)
which has a combinational logic subsection with the following circuit
diagram:
There are two 4-input function generators and one 3-input function
generator, each capable of implementing an arbitrary Boolean function
of its inputs.
The function generators are actually small 16-by-1 and 8-by-1
memories that are used as lookup tables; when the Xilinx device is
"programmed" these memories are filled with the appropriate values so
that each generator produces the desired outputs. The multiplexer
select signals (labeled "Mx" in the diagram) are also set by the
programming process to configure the CLB. After programming, these Mx
signals remain constant during CLB operation.
The following is a list of the possible configurations. For each
configuration indicate how each the control signals should be
programmed, which of the input lines (C1-C4, F1-F4, and G1-G4) are
used, and what output lines (X, Y, or Z) the result(s) appear on.
-
An arbitrary function F of up to four input variables, plus another
arbitrary function G of up to four unrelated input variables, plus a
third arbitrary function H of up to three unrelated input variables.
-
An arbitrary single function of five variables.
-
An arbitrary function of four variables together with some functions
of six variables. Characterize the functions of six variables that
can be implemented.
-
Some functions of up to nine variables. Characterize the functions of
up to nine variables that can be implemented.
-
[Optional challenge] Can every function of six inputs be implemented?
If so, explain how. If not, give a 6-input function and explain why
it can't be implemented in the CLB.






 The inputs are labeled An, Bn, Gn+1, and Ln+1, and the outputs are
labeled Gn and Ln. The G and L signals have the meanings "A greater
than B" and "A less than B," respectively. If both G and L are false,
the meaning is A = B. G and L are never both true. Two k-bit numbers
A and B may be compared using a circuit such as the following:
The inputs are labeled An, Bn, Gn+1, and Ln+1, and the outputs are
labeled Gn and Ln. The G and L signals have the meanings "A greater
than B" and "A less than B," respectively. If both G and L are false,
the meaning is A = B. G and L are never both true. Two k-bit numbers
A and B may be compared using a circuit such as the following:
 The most significant bits are supplied as Ak-1 and
Bk-1, and the least significant bits are A0 and B0.
The output of a comparison is taken from the G and L outputs of the
lowest-order cell (G0 and L0). Gn+1 and Ln+1 of the highest-order
cell are connected to logical 0 to indicate that the numbers are
assumed to be equal until some difference is found between a pair of
bits Ai and Bi.
If the Gn+1 and Ln+1 inputs indicate that higher-order bits have
established A > B or A < B, then cell n must propagate that
result to Gn and Ln. However, if Gn+1 and Ln+1 indicate that the
higher-order bits are equal, then cell n must compare its bit of A and
B to determine if A > B, A < B, or A = B and must signal that
result appropriately at Gn and Ln.
The most significant bits are supplied as Ak-1 and
Bk-1, and the least significant bits are A0 and B0.
The output of a comparison is taken from the G and L outputs of the
lowest-order cell (G0 and L0). Gn+1 and Ln+1 of the highest-order
cell are connected to logical 0 to indicate that the numbers are
assumed to be equal until some difference is found between a pair of
bits Ai and Bi.
If the Gn+1 and Ln+1 inputs indicate that higher-order bits have
established A > B or A < B, then cell n must propagate that
result to Gn and Ln. However, if Gn+1 and Ln+1 indicate that the
higher-order bits are equal, then cell n must compare its bit of A and
B to determine if A > B, A < B, or A = B and must signal that
result appropriately at Gn and Ln.
 Work out expressions for Gn and Ln as functions of Gn+2, Ln+2,
An+1, Bn+1, An, and Bn. Express your answers in the form
Work out expressions for Gn and Ln as functions of Gn+2, Ln+2,
An+1, Bn+1, An, and Bn. Express your answers in the form
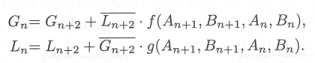
 There are two 4-input function generators and one 3-input function
generator, each capable of implementing an arbitrary Boolean function
of its inputs.
The function generators are actually small 16-by-1 and 8-by-1
memories that are used as lookup tables; when the Xilinx device is
"programmed" these memories are filled with the appropriate values so
that each generator produces the desired outputs. The multiplexer
select signals (labeled "Mx" in the diagram) are also set by the
programming process to configure the CLB. After programming, these Mx
signals remain constant during CLB operation.
The following is a list of the possible configurations. For each
configuration indicate how each the control signals should be
programmed, which of the input lines (C1-C4, F1-F4, and G1-G4) are
used, and what output lines (X, Y, or Z) the result(s) appear on.
There are two 4-input function generators and one 3-input function
generator, each capable of implementing an arbitrary Boolean function
of its inputs.
The function generators are actually small 16-by-1 and 8-by-1
memories that are used as lookup tables; when the Xilinx device is
"programmed" these memories are filled with the appropriate values so
that each generator produces the desired outputs. The multiplexer
select signals (labeled "Mx" in the diagram) are also set by the
programming process to configure the CLB. After programming, these Mx
signals remain constant during CLB operation.
The following is a list of the possible configurations. For each
configuration indicate how each the control signals should be
programmed, which of the input lines (C1-C4, F1-F4, and G1-G4) are
used, and what output lines (X, Y, or Z) the result(s) appear on.