Introduction

This document describes how to perform common tasks in 6.302 using Octave, Scilab, and Matlab. The first two software packages are free alternatives to Matlab, and their use is encouraged.

Each software package employs different methods to create, examine, print, and save transfer functions. For the purposes of this tutorial, we will use the following transfer function as an example:

Octave

GNU Octave is a numerical computation software package very similar to Matlab. In fact, the syntax is almost exactly the same. For help, type help function_name. For an excellent tutorial on control-related functions, type DEMOcontrol.

Creating transfer functions

For the purposes of 6.302, there exist two ways to create transfer functions in Octave. The first is tf2sys, which takes as arguments the coefficients of the numerator and denominator of the transfer function. With the example transfer function, you would type:

Another command is zp2sys, which takes as arguments the zeros, poles, and leading coefficient of the transfer function. Consequently, you would type:

Displaying transfer functions

You will notice that if you merely type L, the output isn't very readable. Use sysout(L, "tf") to display the function in polynomial form and sysout(L, "zp") for zero-pole form.

The graph commands

Root locus

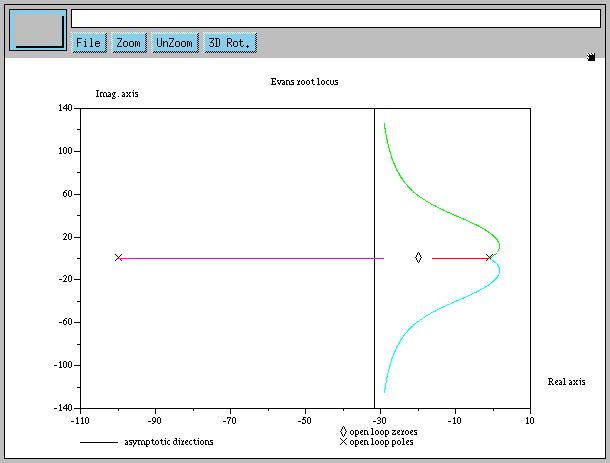
For root locus, use rlocus(L).

L = tf2sys(3e4 * [0.0025 0.1 1], [0.01 1.03 3.03 3.01 1]);
title("Root locus of L");
rlocus(L);

Bode

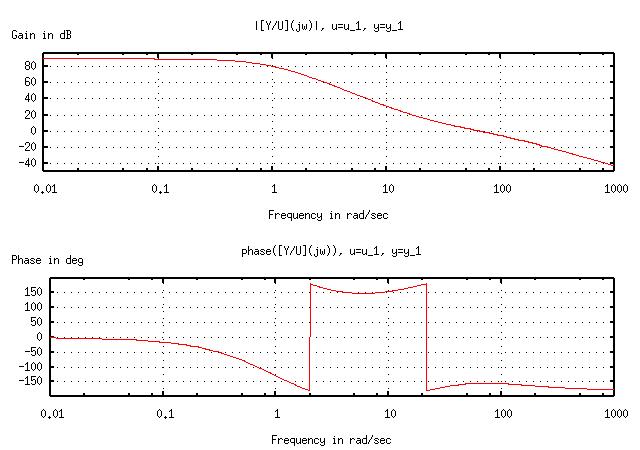
For Bode, use bode(L).

L = tf2sys(3e4 * [0.0025 0.1 1], [0.01 1.03 3.03 3.01 1]);
bode(L);

Nyquist

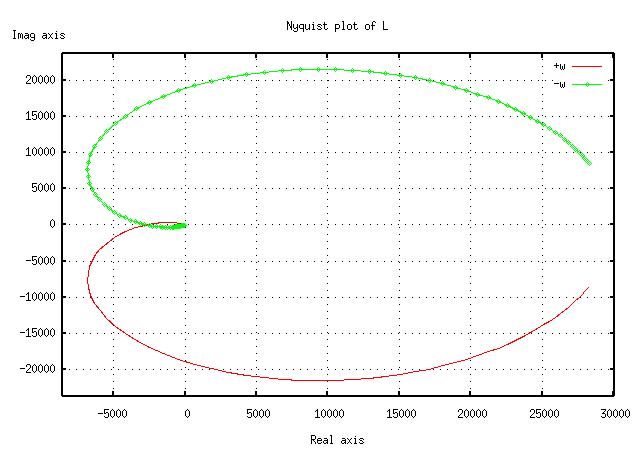
For Nyquist, use nyquist(L).

L = tf2sys(3e4 * [0.0025 0.1 1], [0.01 1.03 3.03 3.01 1]);
nyquist(L, logspace(-1, 1, 100));
title("Nyquist plot of L");
xlabel("Real axis");
ylabel("Imag axis");
replot;

Nichols

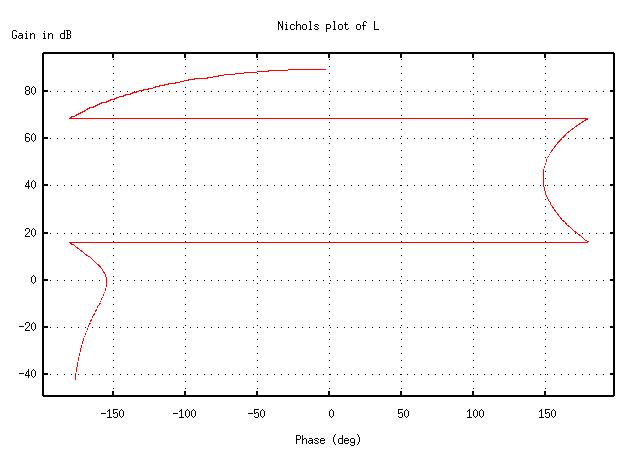
For Nichols, use nichols(L).

L = tf2sys(3e4 * [0.0025 0.1 1], [0.01 1.03 3.03 3.01 1]);
nichols(L);
title("Nichols plot of L");
replot;

Auxilary graph commands

As in Matlab, the commands title, xlabel, and ylabel assign strings to the graphs. Often after these commands, replot is necessary to activate the changes.

However, bode does not work after a replot command; if you find yourself in a situation where a replot is necessary, plot the data from bode manually using plot. (See the online help for details.)

Saving and printing graphs

Octave uses Gnuplot to plot its graphs, so the saving and printing process is not as straightforward as clicking a button.

To save a graph in PNG format (which can be read by almost any graphics program), use the following commands:

gset terminal png;
gset output "filename.png";
replot;

Again, with Bode plots, just use bode(L) again instead of replot.

To print a graph, use the following commands:

gset terminal postscript;
gset output "|lpr";
replot;

After saving or printing, reset the environment with the command gset terminal x11, or else any subsequent graphs will be saved/printed without being displayed onscreen.

SciLab

Scilab is a free software package similar to Maple. Its syntax is considerably different from Matlab, but Scilab can perform symbolic manipulation, unlike Matlab. It includes excellent demos, as found by pressing the "Demos" button on the toolbar.

Creating transfer functions

This is perhaps the easiest task of all. Just type the following:

s = poly(0, "s");
L = syslin('c', 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1)));

The poly command simply defines a polynomial with the symbol "s." Don't forget it! Simply type L to see the transfer function you've just defined.

The graph commands

Root locus

For root locus, use evans(L).

s = poly(0, "s");
L = syslin('c', 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1)));
evans(L, 2.6);

Bode

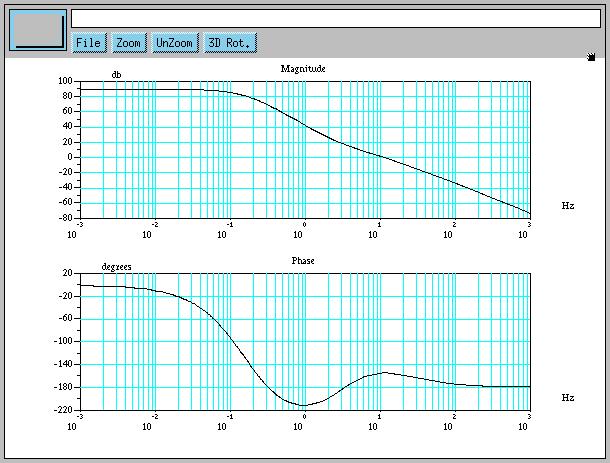
For Bode, use bode(L).

s = poly(0, "s");
L = syslin('c', 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1)));
bode(L);

Nyquist

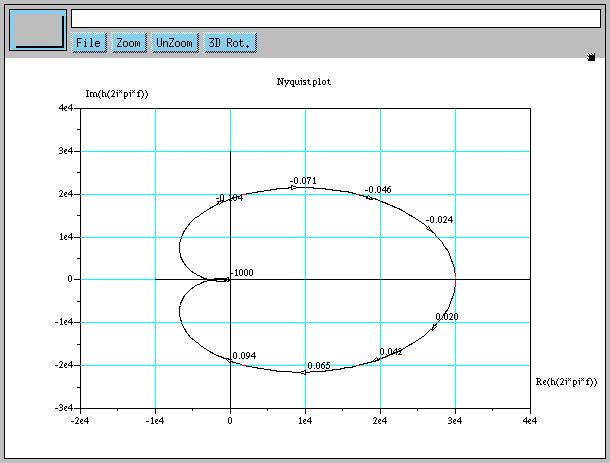
For Nyquist, use nyquist(L).

s = poly(0, "s");
L = syslin('c', 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1)));
nyquist(L);

Nichols

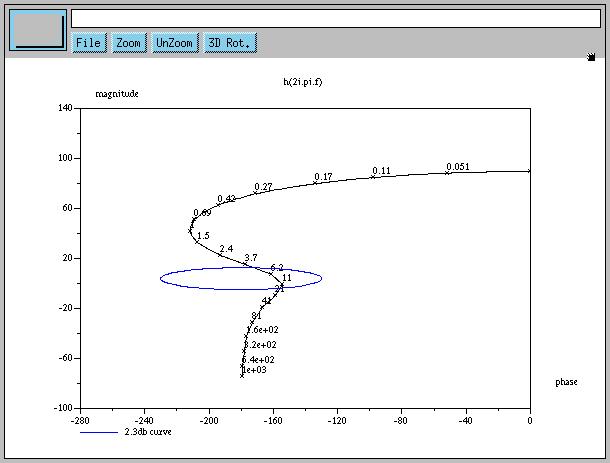
For Nichols, use black(L).

s = poly(0, "s");
L = syslin('c', 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1)));
black(L);

Auxilary graph commands

Unfortunately, there doesn't seem to be any easy way to replace pre-existing titles and axis labels. If you want true customization, consider using plot2d manually.

Saving and printing graphs

Just use the menu items on the graph screens.

Matlab

Matlab is one of the de facto standards of scientific computing. Though it is very powerful, it is unfortunately also very expensive. This is why the availability of packages like Octave and Scilab is so desirable. Nevertheless, the following Matlab material is provided for reference and comparison.

Creating transfer functions

Like Scilab, Matlab makes this relatively easy. Just type the following:

s = tf ('s');
L = 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1));

The graph commands

Root locus

For root locus, use rlocus(L).

s = tf ('s');
L = 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1));
rlocus(L);

Bode

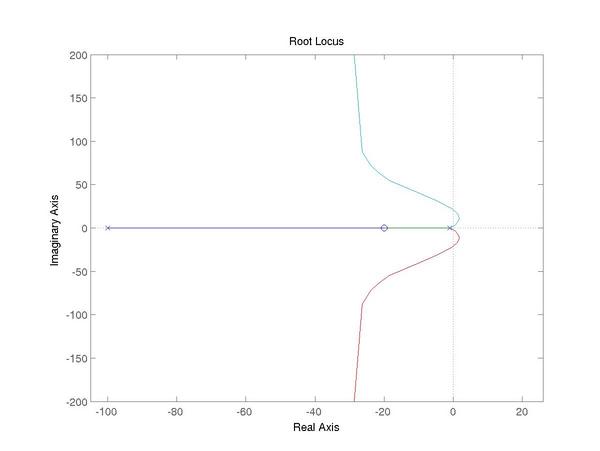
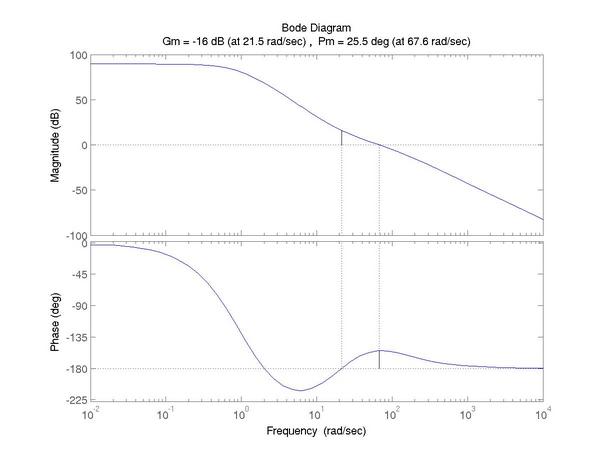
For bode, with margins displayed, use margin(L).

s = tf ('s');
L = 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1));
margin(L);

Nyquist

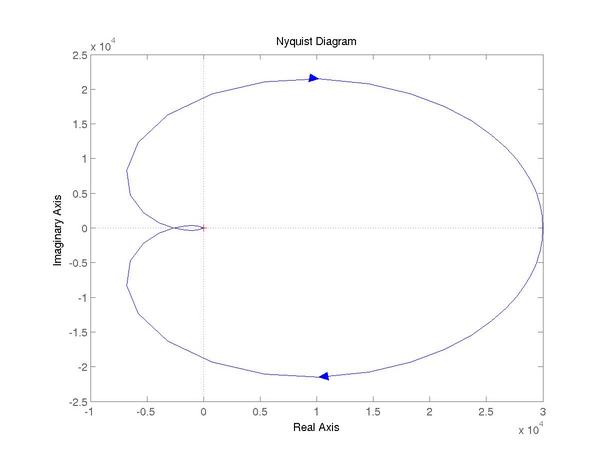
For Nyquist, use nyquist(L).

s = tf ('s');
L = 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1));
nyquist(L);

Nichols

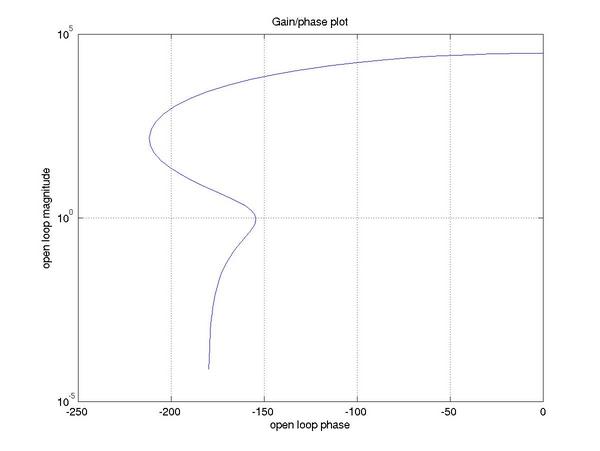
For Nichols, you must calculate the magnitude and phase separately with nichols(L), then explicitly graph it (probably as a semilog plot).

s = tf ('s');
L = 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1));
[m,p,w] = nichols(L);
semilogy (p(:,:), m(:,:));
grid;
title ('Gain/phase plot');
xlabel ('open loop phase (deg)');
ylabel ('open loop magnitude');

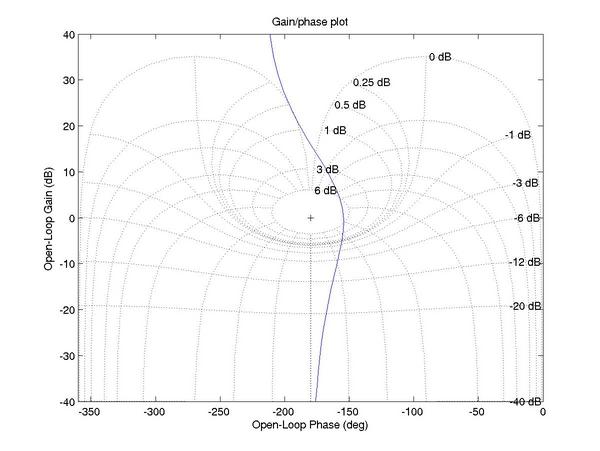
You can also show the Nichols Chart on a dB axis:

s = tf ('s');
L = 3e4 * (0.05*s + 1)^2 / ((s+1)^3 * (0.01*s + 1));
[m,p,w] = nichols(L);
plot (p(:,:), 20*log10 (m(:,:)));
ngrid;
title ('Gain/phase plot');
xlabel ('Open loop Phase (deg)');
ylabel ('Open loop Magnitude (dB)');

Saving and printing graphs

Again like Scilab, Matlab provides a menu interface that makes it easy to save and print graphs as needed.