and 
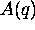, were always described
as vectors, indexed by x and q respectively. In general, these
each could have been described by a matrix, again, with a row index of
of x and q, but with a column index of some independent parameter,
like time.
In the discussion of implementing the Fourier Transform and the
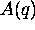Inverse Fourier Transform, and , were always described
as vectors, indexed by x and q respectively. In general, these
each could have been described by a matrix, again, with a row index of
of x and q, but with a column index of some independent parameter,
like time.
For example,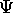 
could have been a matrix. Each column could be for a
different time instance:
then, applying the Fourier Transform procedures exactly as described
previously, we would get a matrix 
instead of the vector
:
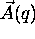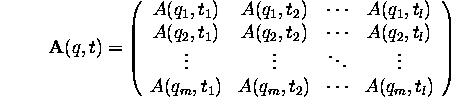
The most probable scenario is that we are given the initial wavepacket
and wish to find the wave packet at time t>0. In this
case we perform the Fourier Transform on a single column, and are
returned a single column amplitude function. Then, we want to find
for many time instances. Using matrices instead of vectors, we
can compute all the time instances at once. First, we setup a matrix
:
This is a matrix, with identical column. Each column is the expsansion
coefficients we computed from the Fourier transform of 
. We will
put one column in the matrix for each future time instance we wish to
compute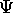 
at.
If we then similarly redefine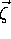 
to account for the time
parameter as follows:
Now, if we perform array multiplication (element by element) on
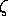and 
we get:
and, if we multiply 
, just like we did in the previous sections:
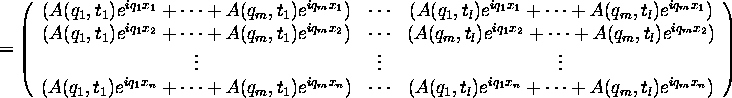
which is just
