Collision Experiments

The web page has the LabVIEW screens from when I did the experiment. You will obtain your own results, but I include mine here in case you might find them useful. Your results may be different.

Part I: Inelastic Collisions

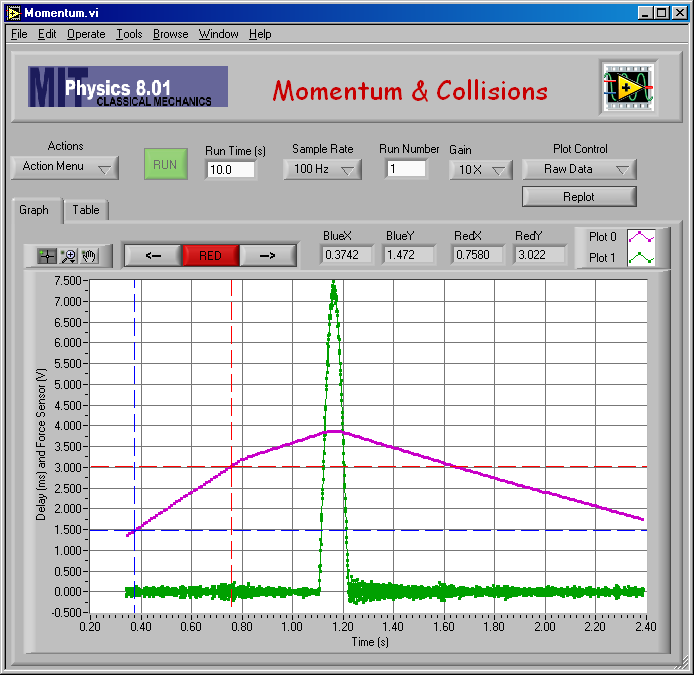
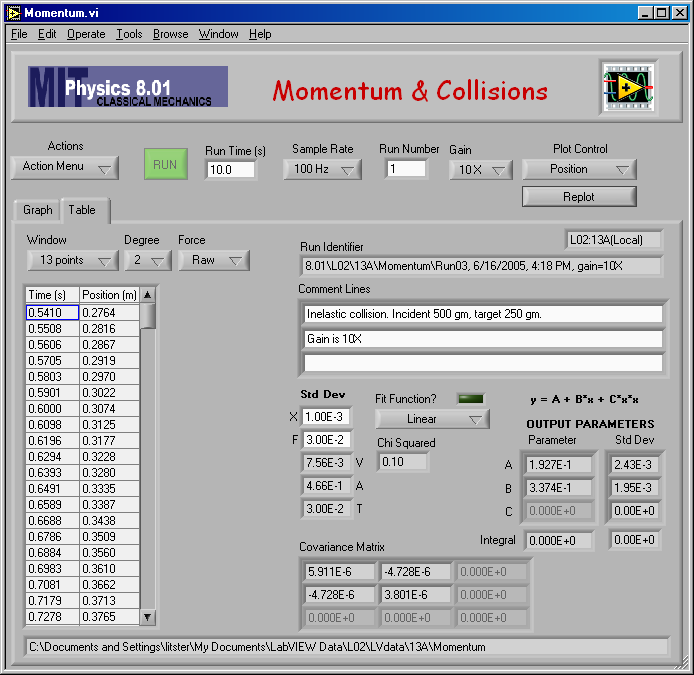
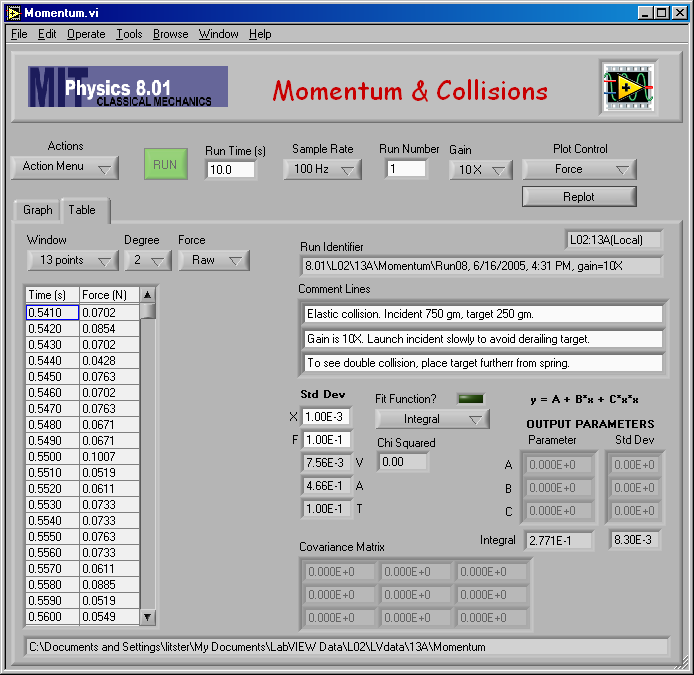
Here are the raw data from my inelastic equal mass measurement. (m_A = m_B = 0.250 kg.)

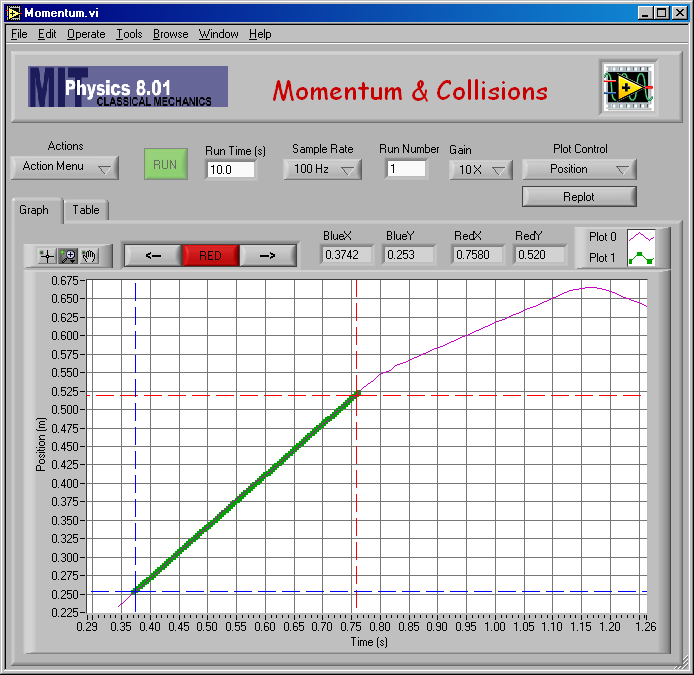
Here is my fit to find v_A,1 for m_A = m_B = 0.250 kg.

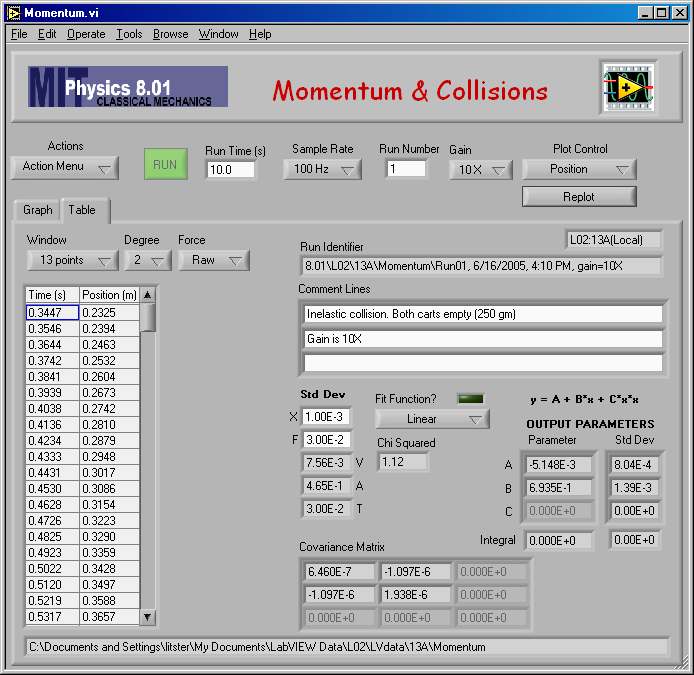
And the numerical result of the fit:

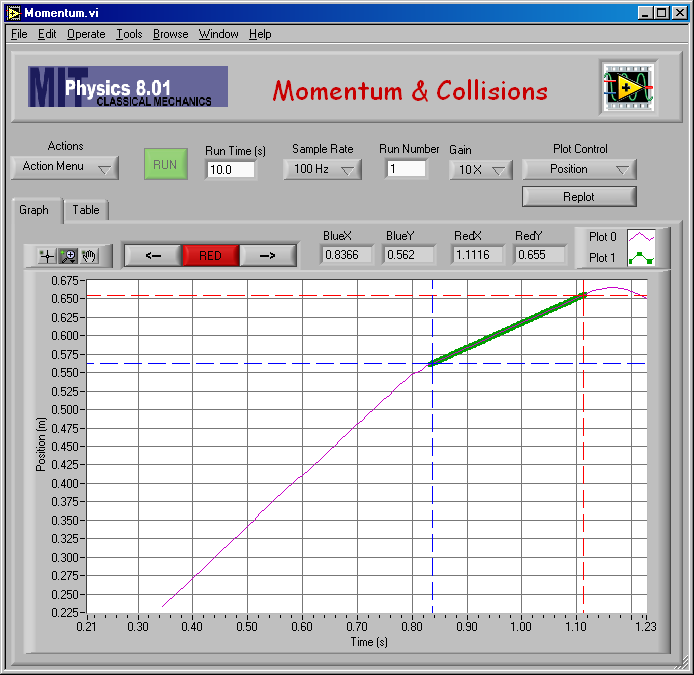
Here is my fit to find v₂ for m_A = m_B = 0.250 kg.

And the numerical result of the fit:

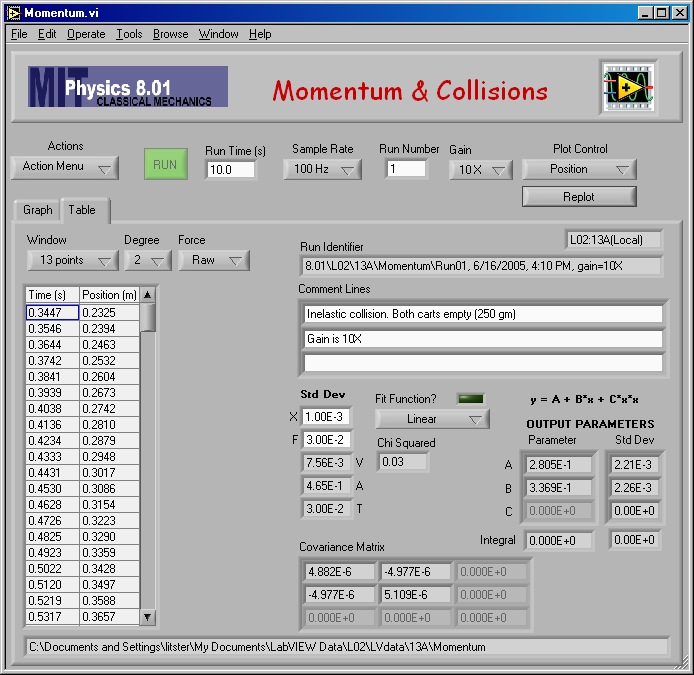
Here is my fit to find v_A,1 for m_A = 0.25 kg and m_B = 0.500 kg.

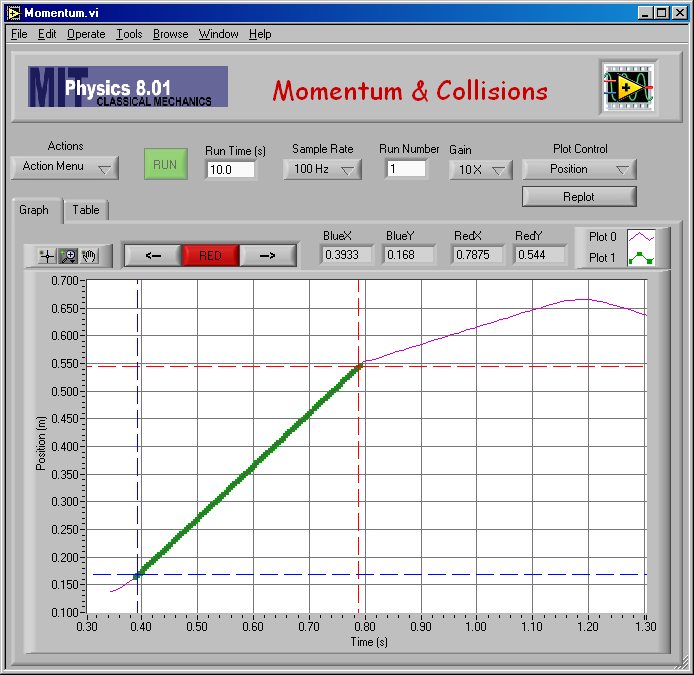
And the numerical result of the fit:

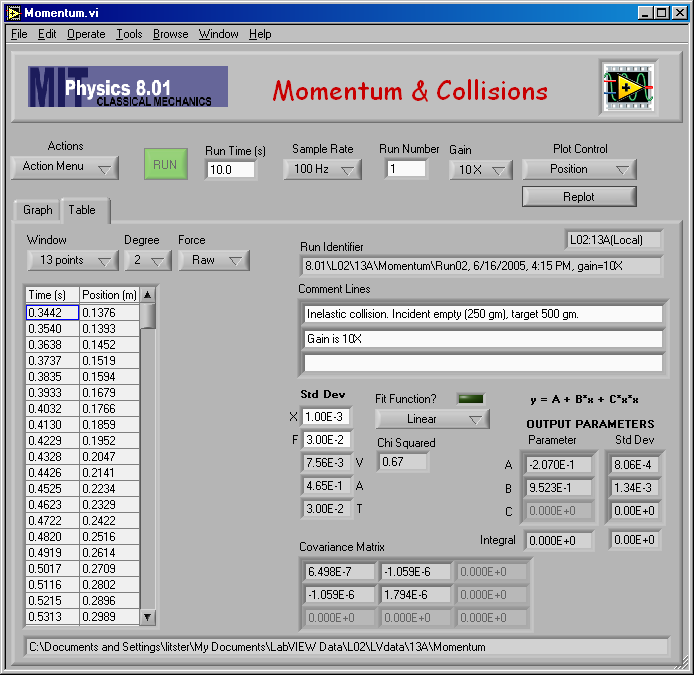
Here is my fit to find v₂ for m_A = 0.25 kg and m_B = 0.500 kg.

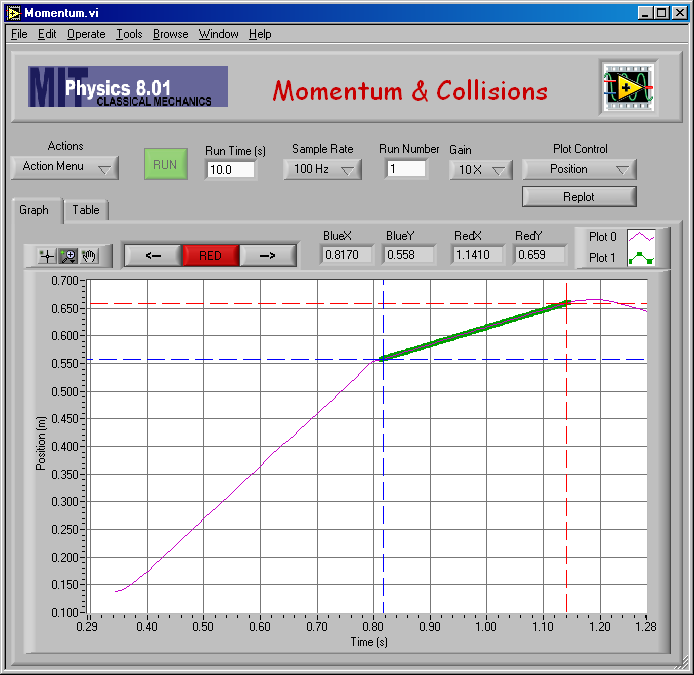
And the numerical result of the fit:

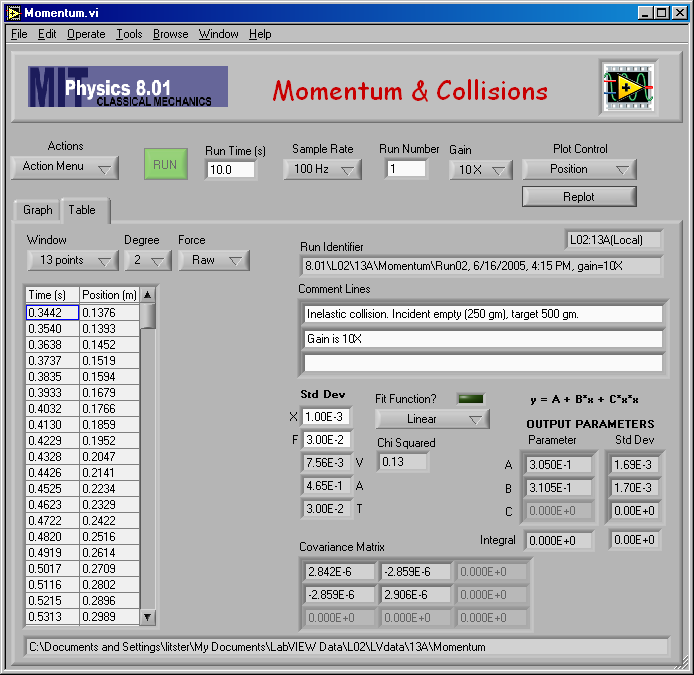
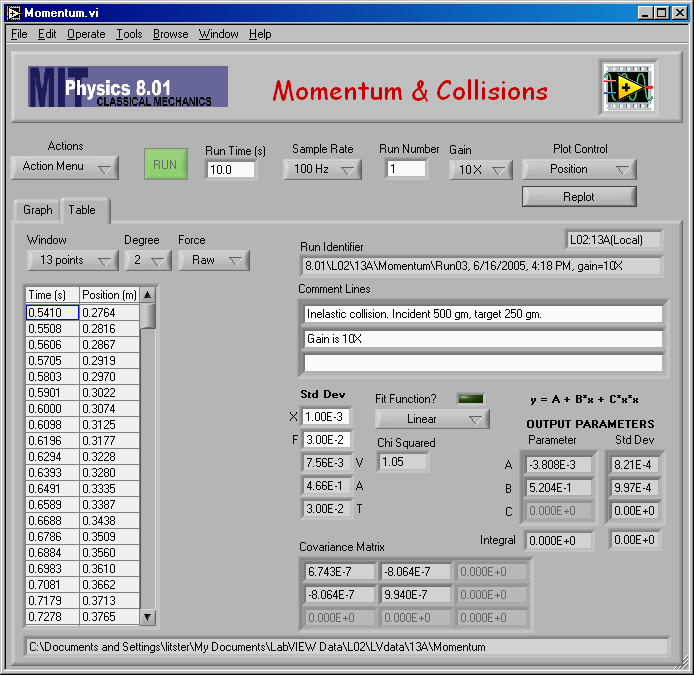
Here is my fit to find v_A,1 for m_A = 0.500 kg and m_B = 0.250 kg.

And the numerical result of the fit:

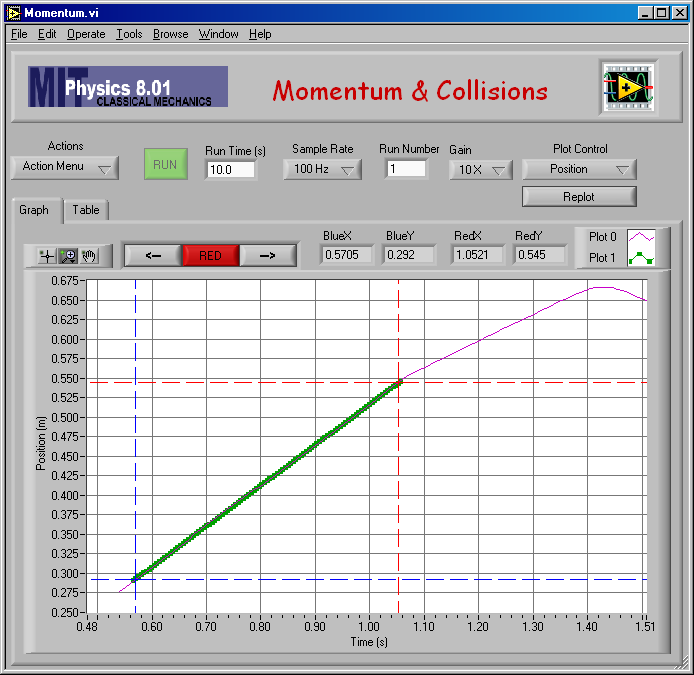
Here is my fit to find v₂ for m_A = 0.500 kg and m_B = 0.250 kg.

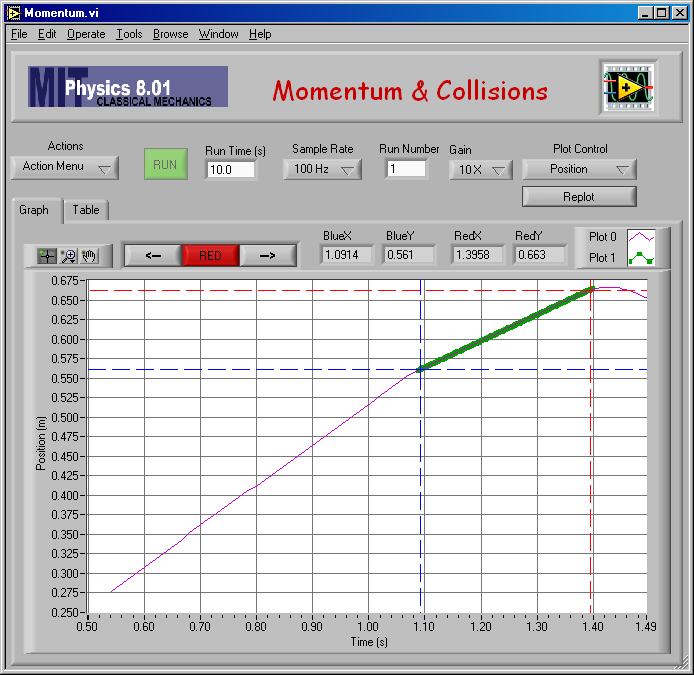
And the numerical result of the fit:

Part II: Elastic Collisions

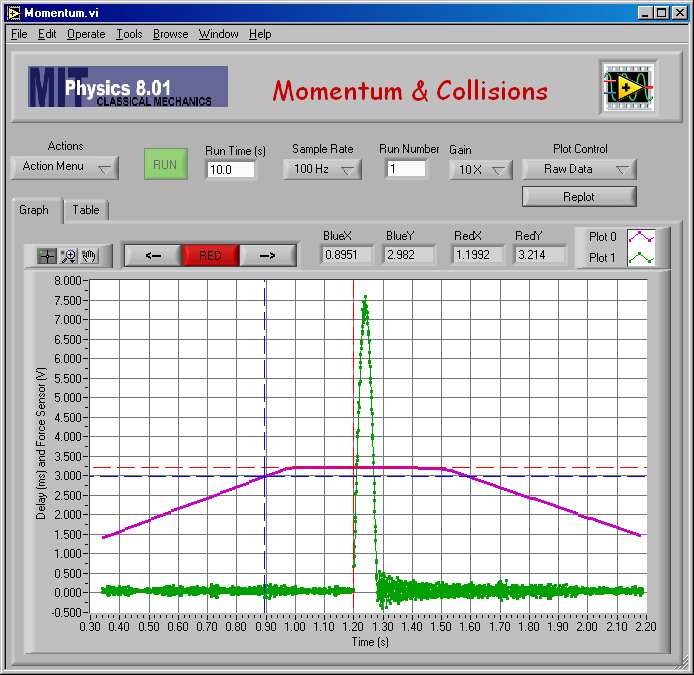
Here are the raw data from my elastic equal mass measurement. (m_A = m_B = 0.250 kg.)

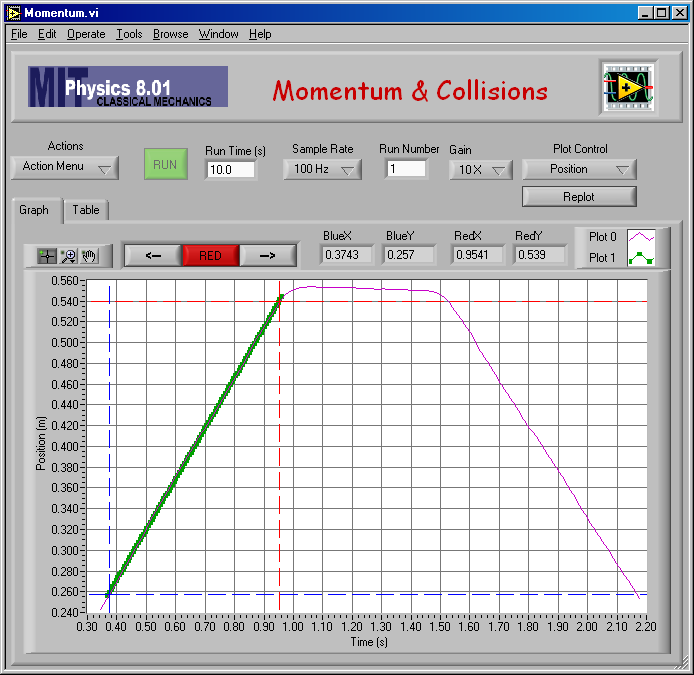
Here is my fit to find v_A,1 for m_A = m_B = 0.250 kg (elastic).

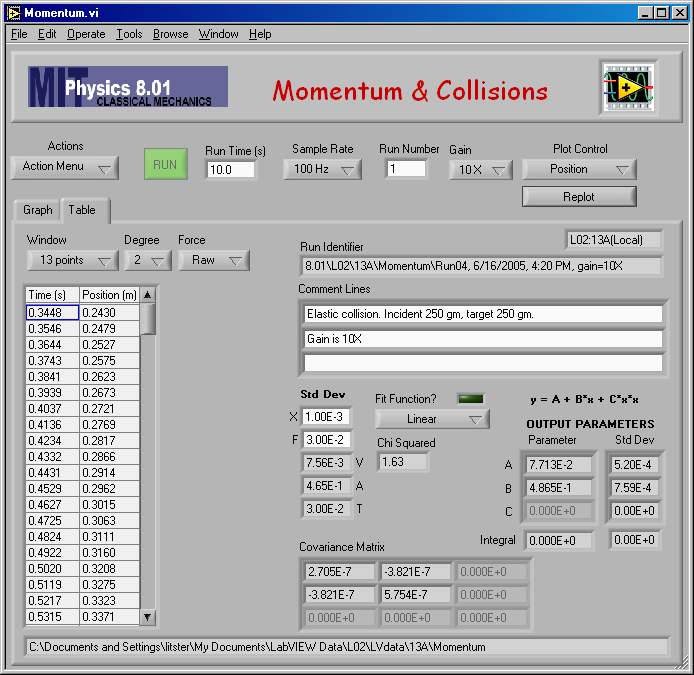
And the numerical result of the fit:

Here is my fit to find v_A,2 for m_A = m_B = 0.250 kg (elastic).

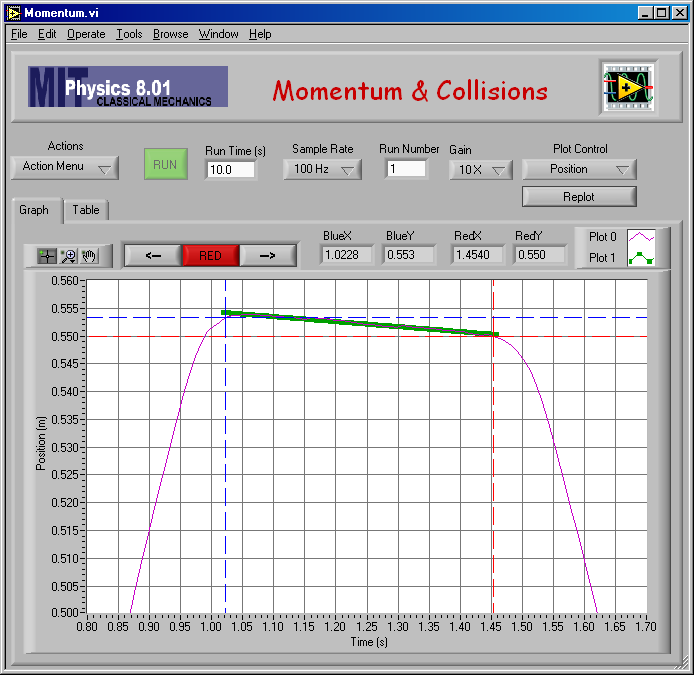
And the numerical result of the fit:

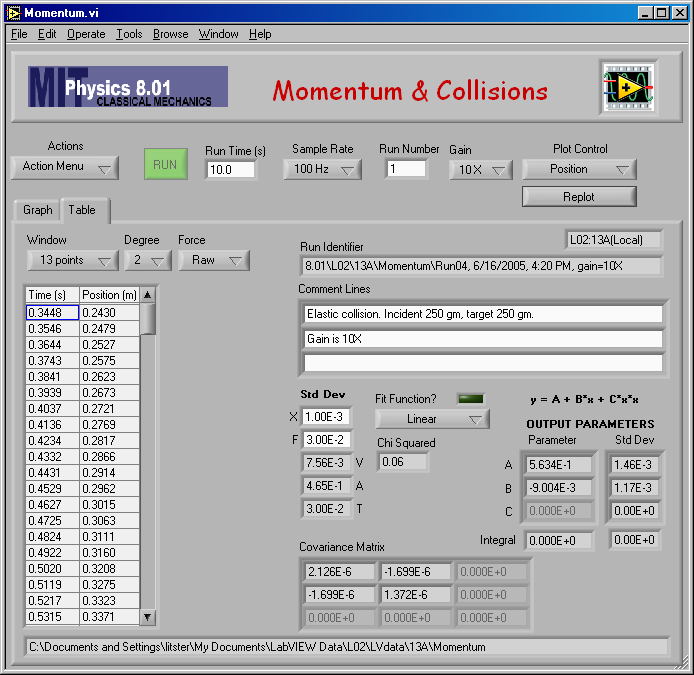
Here is my impulse analysis to find v_B,2 for m_A = m_B = 0.250 kg (elastic).

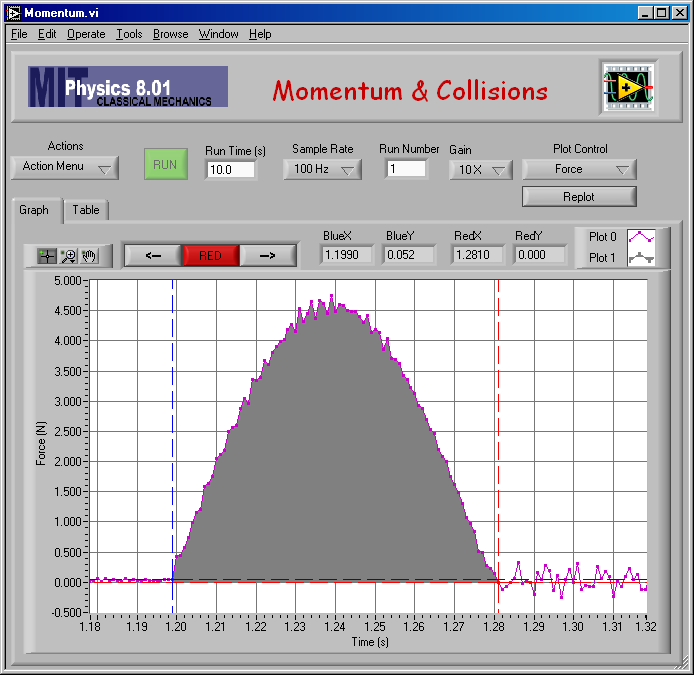
And the numerical result of the analysis:

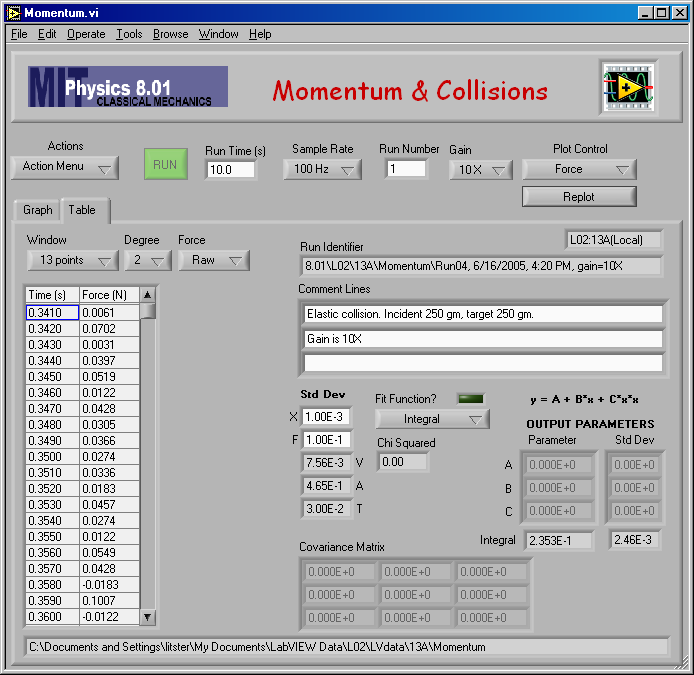
Here is my fit to find v_A,1 for m_A = 0.250 kg and m_B = 0.750 kg (elastic).

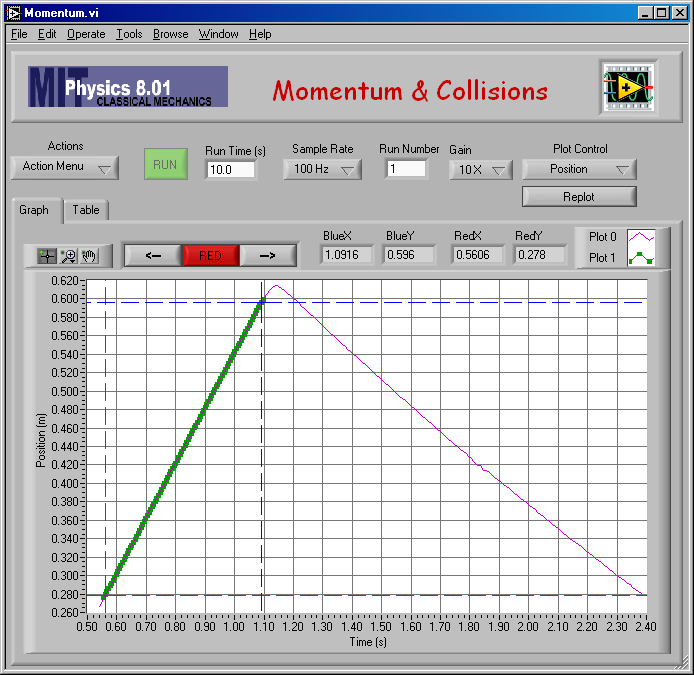
And the numerical result of the fit:

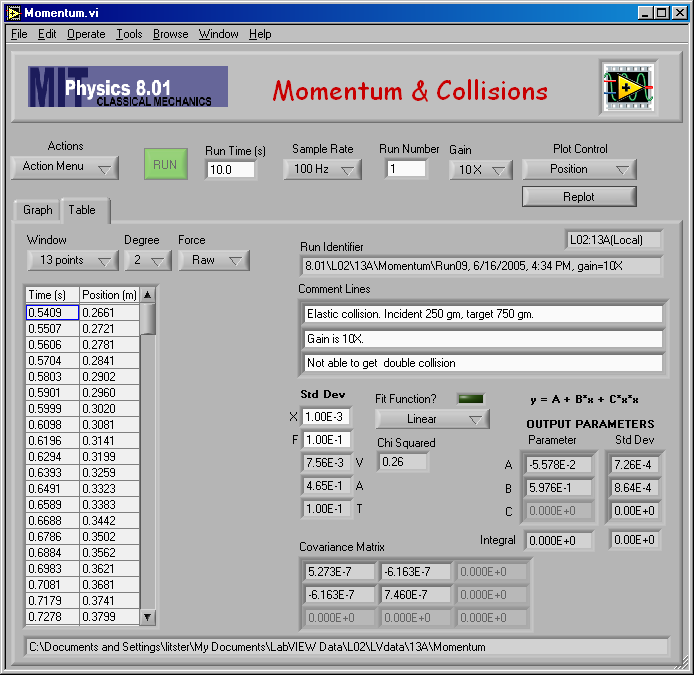
Here is my fit to find v_A,2 for m_A = 0.250 kg and m_B = 0.750 kg (elastic).

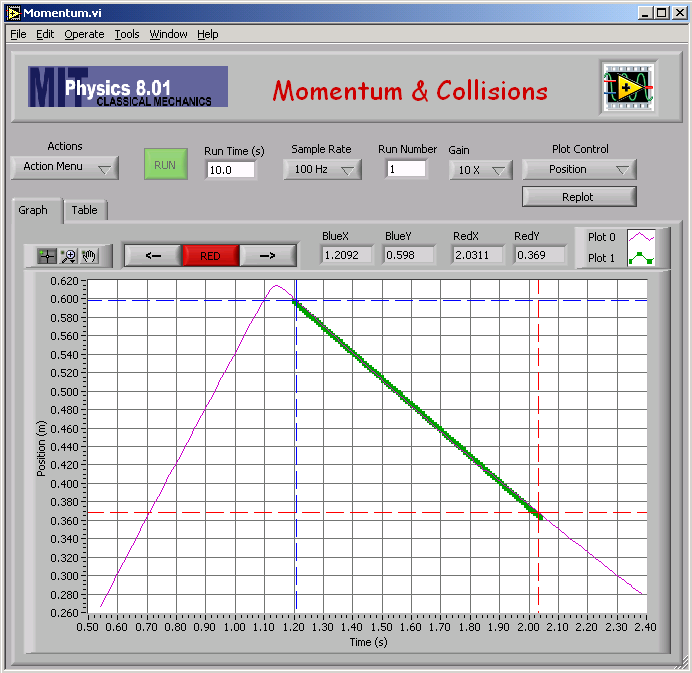
And the numerical result of the fit:

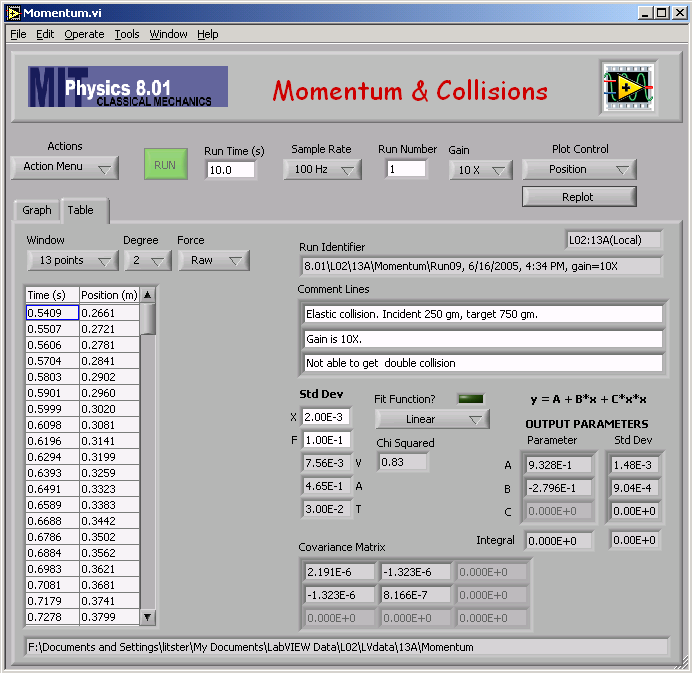
Here is my impulse analysis to find v_B,2 for m_A = 0.250 kg and m_B = 0.750 kg (elastic).

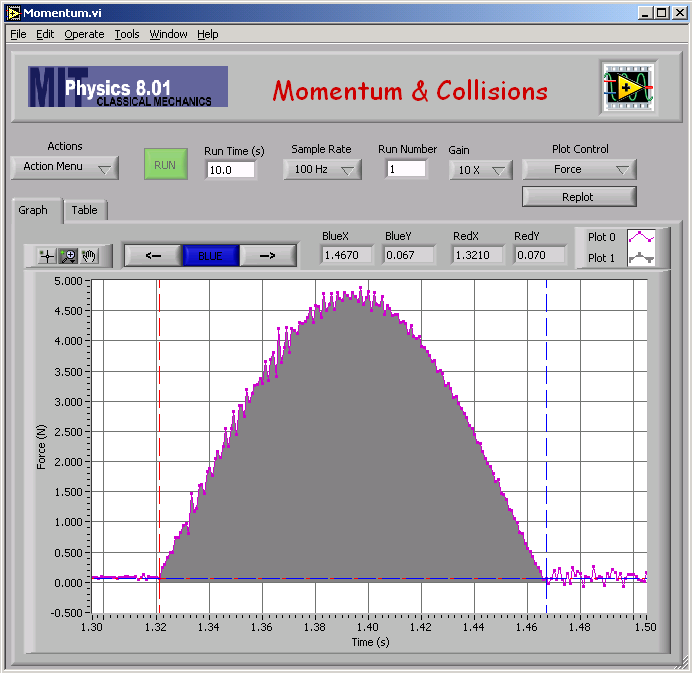
And the numerical result of the analysis:

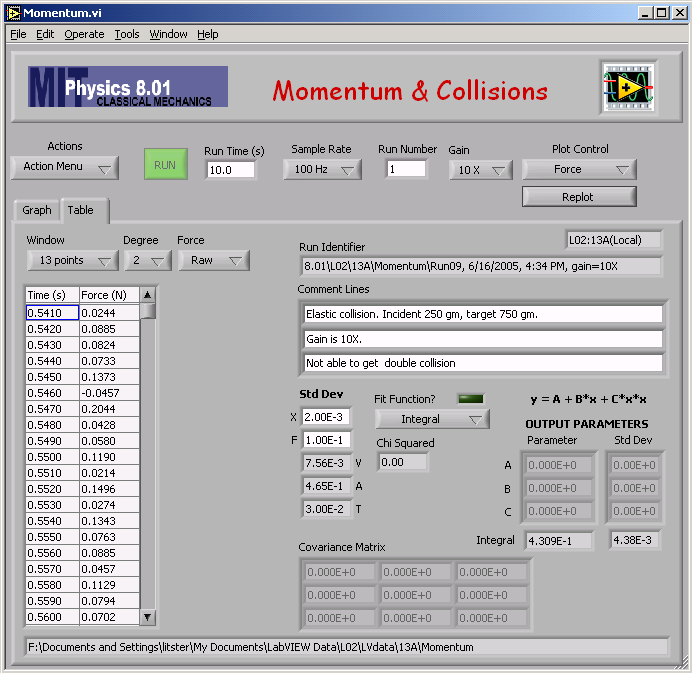
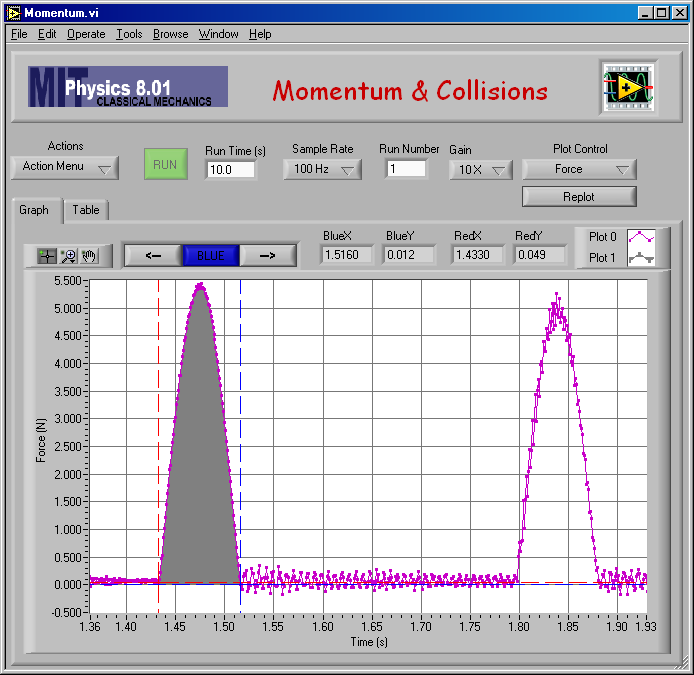
These are the raw data for an elastic collision with m_A = 0.750 kg and m_B = 0.250 kg. If you position cart B correctly and give just the right initial velocity to cart A, you can get three collisions between the carts and cart B will collide twice with the spring. Try and see if you can get this.

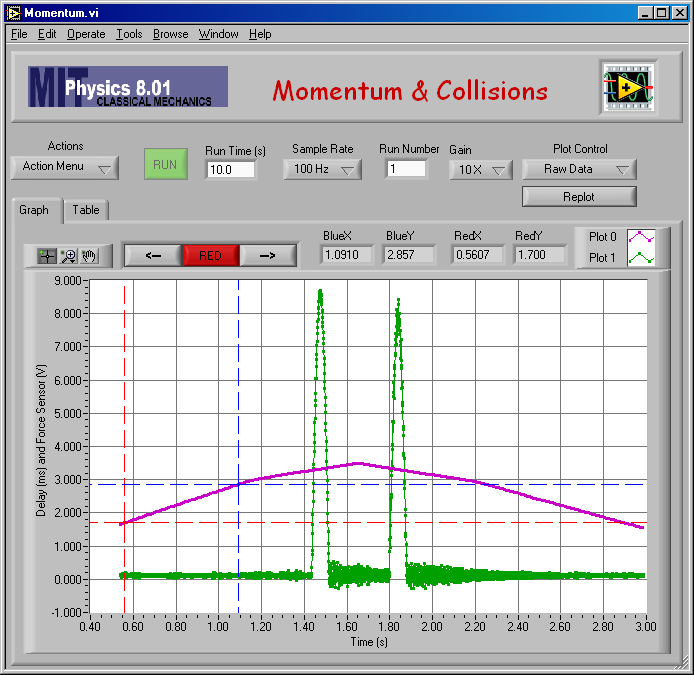
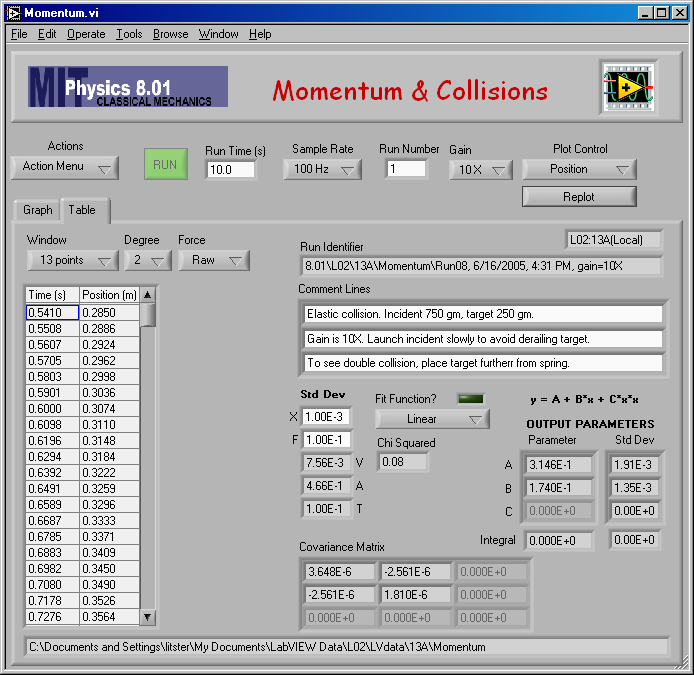
Here is my fit to find v_A,1 for m_A = 0.750 kg and m_B = 0.250 kg (elastic).

And the numerical result of the fit:

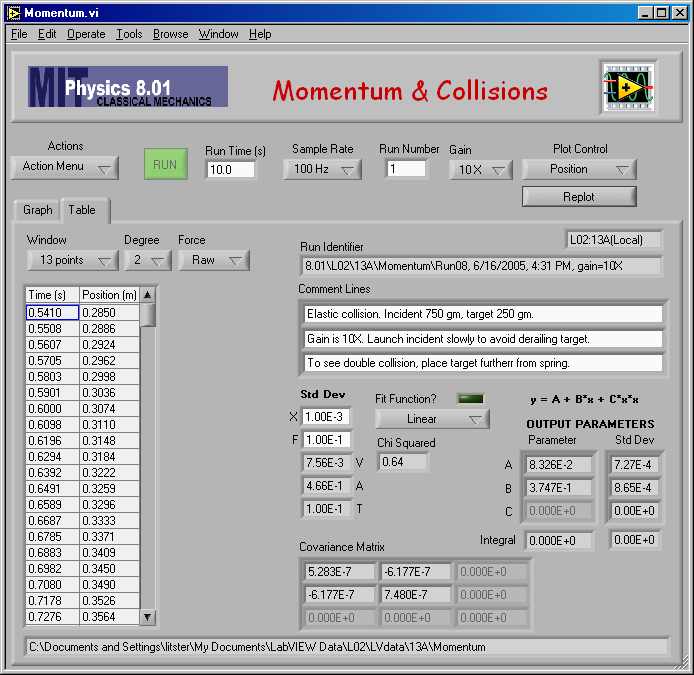
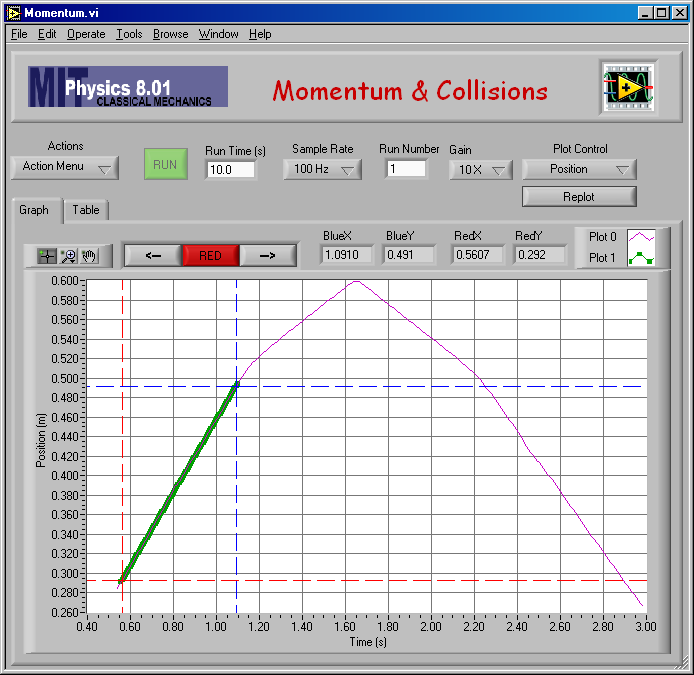
Here is my fit to find v_A,2 for m_A = 0.750 kg and m_B = 0.250 kg (elastic).

And the numerical result of the fit:

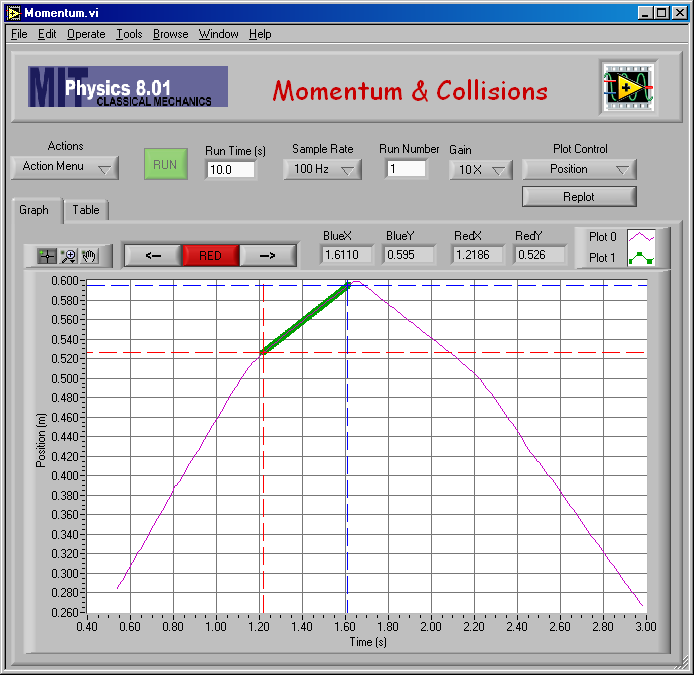
Here is my impulse analysis to find v_B,2 for m_A = 0.750 kg and m_B = 0.250 kg (elastic).

And the numerical result of the analysis:

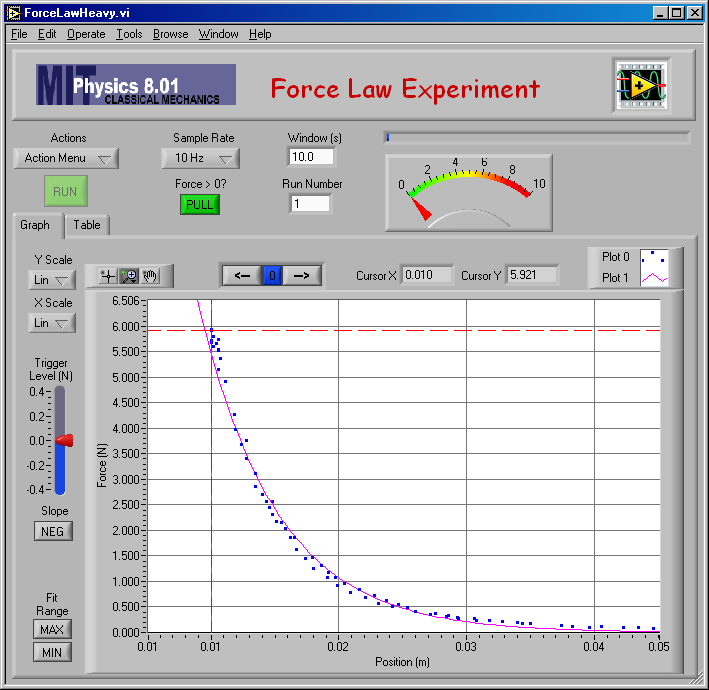
Here are my measurements of the force between two carts that results from the repulsion between the two pairs of magnets. I measured it with a pair of magnets attached to the force sensor instead of the spring, and used a different LabVIEW program called "Force Law Experiment." The purple line is a fit to an exponential function.

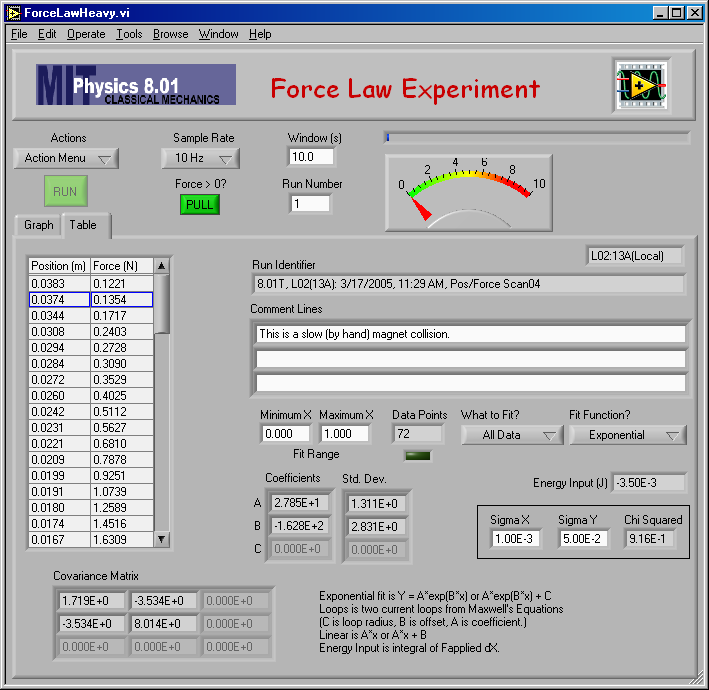
Here are the parameters from the exponential fit.

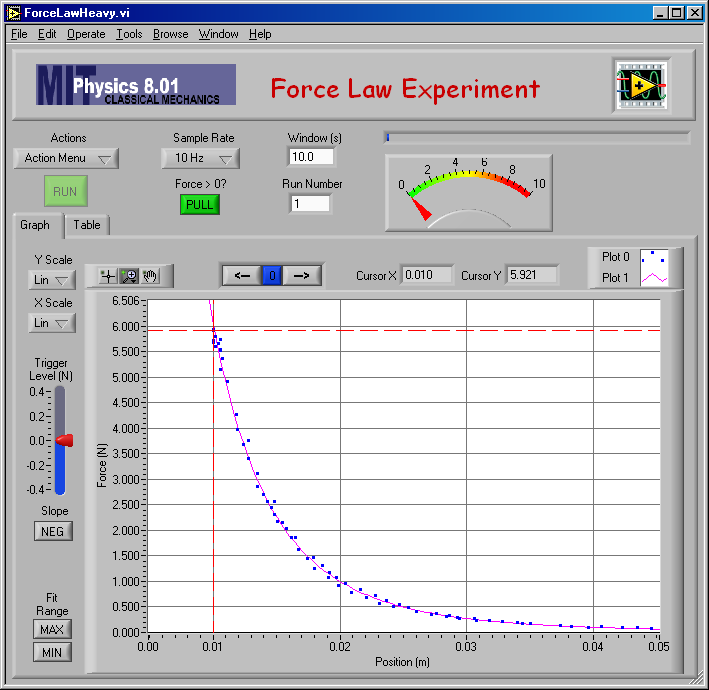
Incidentally, the force between these magnets can be calculated from Maxwell's equations. It's probably beyond what will be covered in 8.02 because it involves elliptic integrals, but if the calculation is done a function results that fits very well. Here is a graph of the fit.

If you want to see a copy of my report, click this link.

J. D. Litster, October 23, 2007.