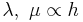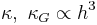Crumpled Surfaces
Table of Contents |
Crumpled Surfaces
Crumpling is something we all are familiar with. We must have crumpled at least one object a day, but how many of us have looked what crumpling exactly makes to a sheet of paper, what structures does it produce to absorb the energy we have put into it?
Imagine a paper sheet confined inside a container. If the container starts so shrink, the foil starts to crumple almost immediately after the container reaches the size of the foil. The crumpled surface have produced sharp corners and edges - vertices and ridges.
What are the significant features of crumpling?
Crumpled surfaces have sharp bends and points as well as almost flat areas. In some sense it is the unique property of a sheets. Imaging confining a wire inside a 2D or 3D container: in both cases it can spread over the container without any sharp singularities. In our 3D world crumpling occur only for 2D sheets, although in higher dimensions 2D sheets can behave like a wire and shrink without singularities.
Why is crumpling so important?
Crumpling is a process of energy distribution. Usually when the energy is allowed to distribute over the system, it prefers to do this uniformly. However there are certain cases, such as turbulence, dielectric discharge, when the energy spontaneously focuses at certain points of the system. The same happens with crumpling: even sufficiently weak perturbation leads to formation of sharp structures.
Basics of elasticity
Elasticity of solids
To describe crumpling we need to know the energy of a distorted medium.
The most native way of describing bulk elastic materials is a natural mapping 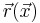 , where
, where 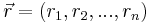 is a position of a particle in space and
is a position of a particle in space and 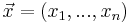 identifies a particle.
identifies a particle.
Configuration r1 = x1,r2 = x2...rn = xn is chosen to have the minimal energy. Then the Hamiltonian can be expanded as the series in the powers of derivatives 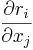 and their order.
and their order.
The energy of the system should be independent of all the symmetry transformations of the system. This includes translations and rotations of both coordinate systems, space and in some cases time reversal.
| Symmetry | Restriction |
|---|---|
| Translational | no 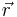 - dependent terms - dependent terms
|
| Space reversal | no linear in 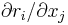 terms terms
|
| Rotational | Only rotational invariants |
For the weak deformation we are left with the terms that are of the second order in 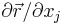 .
.
Let's define a strain tensor 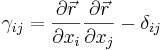 . For this choice γ will be zero for a non-deformed body.
. For this choice γ will be zero for a non-deformed body.
There are two independent terms in this expansion:
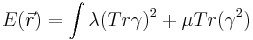
Where the Lame coefficients λ and μ are the properties of material.
The Lame coefficients give us a full description of an elastic deformations. For example, the Young's modulus is Y = μ(3λ + 2μ) / (λ + μ)
Elasticity of thin sheets
Although this equations are still valid for the case of thin surfaces, in this case we want to use another mapping 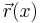 , where
, where  is a space vector, but xi denote coordinates on a surface. Then the above expression will still denote in surface strain energy, but we know that a sheet should also have a bending energy.
is a space vector, but xi denote coordinates on a surface. Then the above expression will still denote in surface strain energy, but we know that a sheet should also have a bending energy.
Up to this order there are no cross-terms that would include both bending and stretching.
Bending is proportional to the curvature, i.e. the rate of change of the tangent to the surface, so it should be composed of 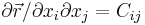 . We construct all possible invariants in the same way:
. We construct all possible invariants in the same way:
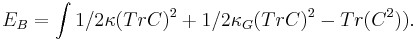
We can make a simple estimate of the coefficients in the above equations. The strain coefficients are proportional to the thickness of the sheet: 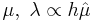 , where
, where 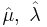 are the solid Lame coefficients.
are the solid Lame coefficients.
Bending of a surface produces a strain, proportional to the thickness h, in a region of width h. Since the energy is proportional to the square of deformation, then the bending coefficient is proportional to h3:
Gaussian curvature
The last term in the bending energy is called Gaussian Curvature. It can be showed that it is proportional to c1c2, where c1 and c2 are two principal curvatures (eigenvalues of a curvature tensor). According to Gauss fundamental theorem of surfaces this term is directly related to the derivatives of strain.
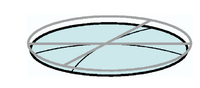
This means that nonzero Gaussian curvature requires the existence of strain. This can be understood in the following way. If both curvatures are of the same sign, then the system is forced to have a form of cap in the vicinity of the point. If they are different, then it is forced to have a saddle form. Both cap-like or saddle-like surfaces requires stretching of the sheet. See an example of a cup-like shape below.
For an unstretchable sheet one of the two principle curvatures is required to vanish everywhere. This means that there should be a straight line passing through every point of a sheet!
Isometric distortions
Isometric regime is a limit of an unstretchable sheet. Remember, that in this limit each point should have a straight line passing through it. We cannot go far enough in this limit if we don't allow our system to have a non-zero strain at certain points. As we will see further, in that case unstrechability requires existence of lines of infinite curvature, connecting different singular points, which leads to infinite energy of a sheet.
D-cones
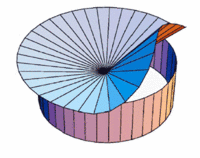
Imagine a circular sheet confined in a cylindrical container that is smaller than the size of the sheet. When the circle cannot fit into container, it forms a so-called d-cone. Part of this d-cone is a conical surface; part of it forms a buckled region. The surface deforms so that it avoids stretching almost everywhere! This shape have only one singular point: the deformations at this point are infinite. If you look at a crumpled sheet of paper, you can see that this d-cones are essentially the building blocks of the crumpled surface.
Energy of a d-cone is logarithmically divergent, and in a real system a d-cone will have a core of a certain size to eliminate this divergence. In the core the influence of stretching will be important. The size of this region will be estimated later from a scaling assumptions.
Systems with many vertices
Then consider a more difficult system: a sheet with two d-cones. The picture on the right is a result of a computer simulations in an unstretchable limit.
To analyze it's property recall that in this limit there should be a straight line passing through each point; lines can terminate only at a surface or at singularities. Consider a point in a vicinity of one cone. Two straight lines should be passing through this point, connecting it to both vertexes. This is possible only if a region between two cones is plain.
Now there are two planes to the both sides of the vertexes. This two planes should intersect and form a sharp ridge, at which curvature is infinite.
Now we can imply something about the properties of an ideal crumpled sheet:
-It contains some number of vertexes
-Vertexes are connected by ridges
-Surface between vertexes and ridges is flat
Scaling properties
Further analysis is needed to describe the real crumpled system of a nonzero width. Scaling arguments can provide much information about the behavior of the system.
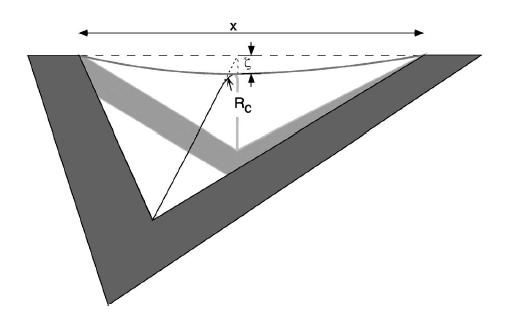
To analyze scaling properties we consider a special shape of a sheet, called kite. A kite is a simple model of a ridge. Imaging a sheet attached to rigid square frame of a size X, that could be bent along it's diagonal.
By making this simple experiment with a paper sheet one can see, that the width of the bending area is significantly smaller that the size of the frame, X, but larger that the thickness of the paper h. Let's denote the size of the bent region as w. This distance is responsible for the bending energy of the system.
Let's define a baseline as a straight line passing through the two edges of the kite.
One can see, that the ridge line of the kite should sag under the baseline to account for a smooth bending region. The sag ξ should be of the order of w, the size of the bending region, which is roughly the radius of curvature RC. This sag is responsible for stretching the ridge line.
The length of the ridge line is increased:
L = X(1 + O((RC / X)2))
Which gives an average strain of a ridge line of the order of (RC / X)2.
Then the stretching energy is proportional to strain modulus x length x width x strain squared:
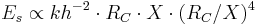
If the bending region is of the size R_C, then average curvature is proportional to 1 / RC. Then the bending energy is proportional to bending modulus x length x width x curvature squared:
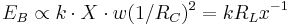
By minimizing the sum of these two energies we can get a surprising result:
EB = 5ES.
The energy stored in bending is 5 times more that the energy stored in stretching, and this ratio is independent of the sheet thickness or width. This is an analog of a virial theorem.
This result shows that stretching plays an essential role in crumpling even for an almost unstretchable sheet!
The other result of scaling is the inverse curvature of a bending region:
RC = X(h / X)1 / 3
The size of the bending region indeed goes to zero in the limit of a thin sheet.
Conclusion
In this review we've analyzed a properties of a system with a broken symmetry using simple scaling and geometrical arguments. The results proven are quite universal and are consistent with experiments and numerical analysis. This shows, that the symmetry breaking indeed have some universal properties that are independent of a particular realization.