Universality

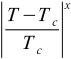
When we started talking about critical opalescence, we spoke of water and carbon dioxide and the gas-liquid transition. The experiment described something different – two different liquids going through a “dissolved/not-dissolved” transition. But everything we understood about critical phenomena from the liquid-gas transition seemed to work in the experiment.

The connection is deeper than that. If you look at the way response functions like compressibility get big around the critical point (how fast as you bring the temperature close to the critical point), you find that you end up with the same numbers for lots of very diverse situations.

As scientists, we have to take one more important step: we have to be a little more concrete in the description of “sameness”. This requires a little math, but it’s totally worth the effort. So here it goes: things get big (diverge) around the critical temperature as

Ask yourself...

• What happens to this quantity as T gets closer to T_c?
  • As T gets close to T_c, the function diverges or “blows up” (gets really big).
• There are three lines below corresponding to three different values of the critical exponent, x. Match the line to the critical exponent.

• The critical exponent controls how fast the function blows up. The bigger the exponent, the faster the blow up. A gas-liquid critical point, like that for water or carbon dioxide, is associated with a bunch of different critical exponents – one for isothermal compressibility, one for heat capacity, and so on. We just recycle the same function with a different x.
Click here to hide the answers.

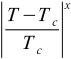
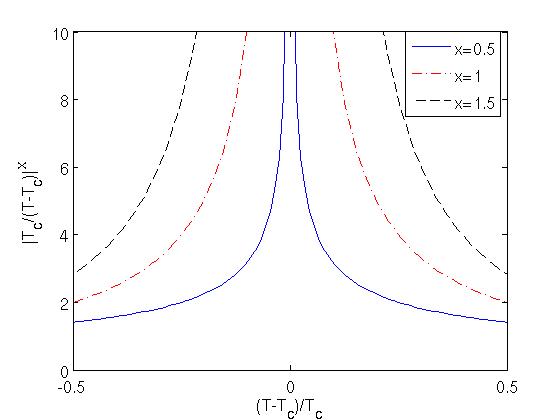
The remarkable thing about critical phenomena is that a bunch of different kinds of quantities – response functions like compressibility and others – follow this rule close to the critical temperature. There might be a different critical exponent for each different kind of quantity, but the same kind of expression represents the behavior of all of these quantities.

The even more remarkable thing is that the critical exponents – the x's – for totally different systems are the same.

You might not expect carbon dioxide and water to have the same set of critical exponents, because they’re two different substances. But they do, and, in fact, these same numbers would come out of the binary liquid experiment. There are more exotic-sounding phase transitions, too, like those of binary metal alloys or the paramagnetic-ferromagnetic crossover. These things seem really different from one another (think how different water is from methyl alcohol – you need to drink water or you’ll die, and you die if you drink methyl alcohol! And what did that experiment have to do with magnets?), yet the numbers coming out of experiments are exactly the same.

Ask yourself…

• What happens at the critical point that is always the same?
• What all of these situations have in common are fluctuations about an average state (temperature and pressure). Right around the critical point, these fluctuations become magnified, and control the way the system behaves. Because the fluctuations grow in the same way – whether they are fluctuations of average density or magnetization or any other order parameter – the same rate of growth appears for all of these systems….WOW!

….or something like that – it’s a little more complicated. It turns out that the critical behavior is not always the same, but it doesn’t depend so much on the identity of the substance at play – more on its dimensionality and number of components.

WHAT?

More on this later.

Click here to hide the answers.

To gain further understanding, we need to open up this black box of fluctuations to figure out what is happening around the critical point that makes them grow so large.