Volfram MathWorld has good explanations for the frequently-used mathematical jargons topology, homotopy and homotopy group. However, these explanations themselves are also full of mathematical terms, so it's not very friendly. Let's try a different approach, starting with the definition of order parameter
To describe the dynamics of a physical system, one needs to keep track of the important degrees of freedom, the important variables. For example, in crystion, the important degree of freedom are the motion of the atoms away from their lattice positions; in a magnet, it's the local direction of the magnetization (represented by an arrow pointing to the North end of the local magnet); ... These variables are called order parameters and the combination of them in a region can be an order parameter field. To see the mapping between physical configuration space and the order parmater field, consider a magnetic material at a given temperature so that the local magnetization is fixed:
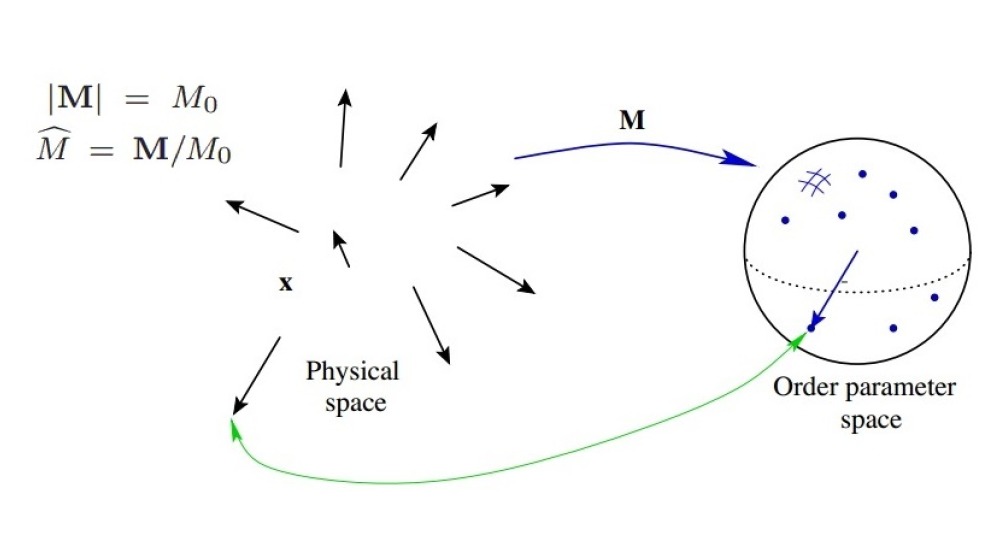
The length of the magnetization vectors (an arrow at each points in space) therefore has a fix length as a constrain, and only the direction of these vectors controls the Physics of the system. One can take the angular direction of the magnetization to be the order parameter, and the current state of the material is described by this order parameter field. This whole procedure can be view as mapping information in physical space into points in the order parameter space, and in the case above one maps the magnetization vector field into points on a space.
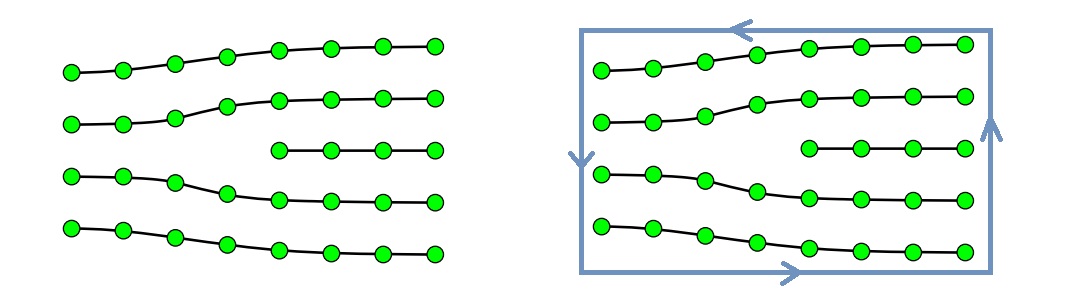
Now, it's ready to define a general defect and a topological defect. A general defect is a tear in the order parameter space (in the sense that the mapping between physical space and order parameter space is non-trivial or cannot be done in a small region, or, the order parameter space itself has a singular or non-continous behavior), and a topological defect is a tear that cannot be patched (and the detail properties of this unpatchable nature can be explained and well-understood from the study of topology). Consider a piece of 2D crystal above: move from left to right, there's an extra row of atoms originated from a dislocation in the middle, which means it's a defect, in general. Since away from this tear the crystal looks fine as the distortion doesn't really make the square grids and the order parameters harder to see, one might expect to be able to rearrange the atoms in a small region around the start of the extra row and patched the defect. However, this wishful action can not be done, since one can tell there must be an extra row without knowing exactly the position of the defect by counting the number of rows on the right and on the left (in general, one draw a large loop surrounding the defect and count the net number of rows crossed by the loop). In this example, in the shown region it's 4 comes from the left and 5 comes from the right, and indeed no matter how far-left we stay from the center, there will always be an extra row from the right. Therefore, there's no way to patch this defect unless changing the whole crystal structure, and this defect is a topological defect. Topology is associated with the patching procedure.
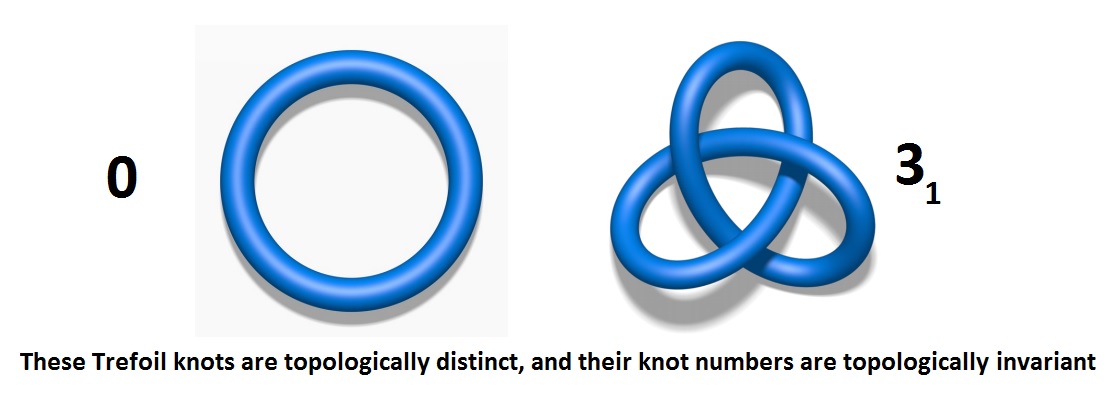
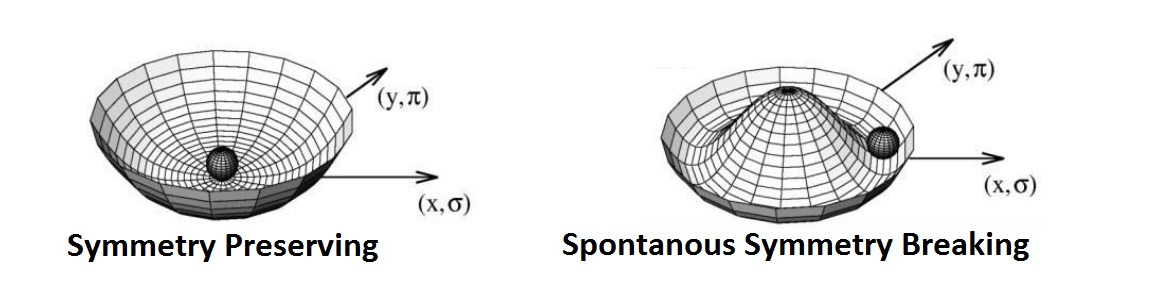
In a more general sense, topology is the study of curves, surfaces and higher dimensional structures where bending and twisting is ignored. With homotopy and homotopy group, one can classify different topological defects by associating each defect to a label (which is topologically invariant), and usually this label has physical meaning, playing an important realization in the interaction between topological defects with themselves and other objects in the theory. . A more detail study of this will be done in another part of this Website. Note that topological defects comes from the structure of order parameter space, which is used to describe ordered matter - a symmetry based system. Since order originates from broken symmetry, a later part in this section will deal with symmetry breaking: