Alejandra Uranga Research Engineer Gas Turbine Laboratory Department of Aeronautics and Astronautics Massachusetts Institute of Technology 77 Massachusetts Avenue, Room 31-268 Cambridge, MA 02139, USA E-mail:  auranga@mit.edu

Research

Aircraft and Technology Concepts for an N+3 Subsonic Transport

We are designing, developping, simulating, and wind-tunnel testing the D8 "double-bubble" concept, an inovative aircraft configuration aimed for a service entry in the 2025-2035 timeframe which has the potential to provide significant reductions in fuel burn, emissions, and noise.


... more details coming soon...

Implicit Large Eddy Simulation of Flow Around an SD7003 Wing

My PhD research involved the use of high-order Discontinuous Galerkin methods for the simulation of transition to turbulence in flows at low and moderate Reynolds numbers. My thesis work was supervised by Jaime Peraire and Mark Drela of MIT, and I work closely with Per-Olof Persson of UC Berkeley.

You will find here some of the results. The interested reader is referred to the following publications:

• A. Uranga, P.-O. Persson, M. Drela, and J. Peraire,
  "Preliminary Investigation Into the Effects of Cross-Flow on Low Reynolds Number Transition",
  20th AIAA Computational Fluid Dynamics Conference, AIAA-2011-3558, Honolulu, Hawaii, June 27-30, 2011.

• A. Uranga, P.-O. Persson, M. Drela, and J. Peraire,
  "Implicit Large Eddy Simulation of transition to turbulence at low Reynolds numbers using a Discontinuous Galerkin method",
  International Journal for Numerical Methods in Engineering, Vol. 86, 2011

• A. Uranga, P.-O. Persson, M. Drela, and J. Peraire,
  "Implicit Large Eddy Simulation of transitional flows over airfoils and wings",
  19th AIAA Computational Fluid Dynamics Conference, AIAA-2009-4131, San Antonio, Texas, June 22-25, 2009.

Numerical Method   -   Problem Setup   -   Computational Grid   -   Results   -   Animations   -   References

Numerical Method

The compressible, unsteady, Navier-Stokes equations are solved using a high-order Discontinuous Galerkin (DG) method. The inviscid terms of the numerical fluxes are evaluated with a Roe solver [9], while viscous terms are treated using the Compact Discontinuous Galerkin (CDG) method [7]. The later is a compact method that results in a sparser connectivity matrix than the alternative methods such as the BR2 method [2] and the Local Discontinuous Galerkin (LDG) method [3].

Time integration is performed using the third-order accurate diagonal implicit Runge-Kutta (DIRK) scheme [1]. The non-linear system of equations is solved using Newton's method with a block-ILU/multigrid preconditioned Conjugate Gradient Squared (CGS) solver for the each linear iteration [8].

Following the implicit Large Eddy Simulation (ILES) approach, the fully (unfiltered) compressible Navier-Stokes equations are solved; the unresolved small eddies are accounted for by means of the numerical dissipation, and no sub-grid-scale model is employed.

Problem Setup

The flow aroung a rectangular wing with an SD7003 airfoil profile is considered, at an angle of attack of 4 degrees, and at Reynolds numbers of 10,000 and 60,000.

The freestream Mach number is set to 0.2, which is low enough that the flow is fundamentally incompressible but high enough to improve numerical stability. The fluid is air with a Prandtl number of 0.72 and specific heat ratio of 1.4, and the kinematic viscosity is assumed constant.

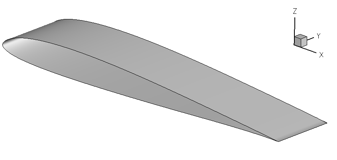
The axes are setup as shown in the figure, with x being the chord-wise direction (with the leading-edge at x=0), y the span-wise direction, and z is vertically up. The wing span-to-chord ratio is set to 0.2, following the findings of Galbraith and Visbal [5]. Extensive experimental data is available for comparison [6], as well as numerical simulations [5].

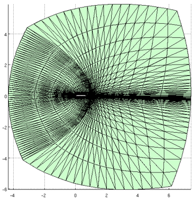
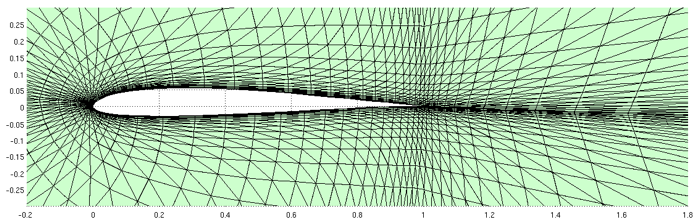
Computational Grid

The computational domain has periodic boundary conditions along the span-wise direction, in order to simulate an infinite wing. The wing's surface is represented by a non-slip, adiabatic, boundary condition, while a full-state type boundary condition is imposed at the far-field of the computational domain.

The computational domain extends 4.3 chord lengths upstream of the wing's leading edge, 5.9 chord lengths above the wing's leading edge line, 6.0 chord lengths below the wing's leading edge line, and 6.43 chord lengths downstream of the wing's trailing edge. Thus, if we denote by c the chord length, the domain spans on the range [-4.3c , 7.4c] x [0 , 0.2c] x [-6.0c , 5.9c] along the chord-wise, span-wise, and vertical directions, respectively. The results that follow where obtained on a computational grid with 52,800 tetrahedral elements and 1,056,000 degrees-of-freedom. Third-order polynomials are used, thus resulting in a fourth-order accurate method in space. The following images show the computational grid on a planar cut along the span-wise direction.

Results

At a Reynolds number of 10,000 the flow is found to be fundamentally two-dimensional with little variation along the spanwise direction and close-to-periodic vortex shedding.

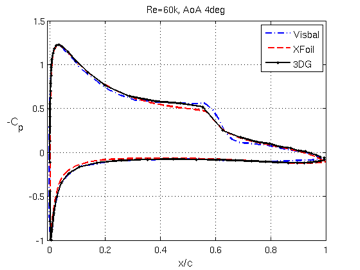
On the contrary, at a Reynolds number of 60,000, three-dimensional structures are present as made visible by contours of vorticity or q-criterion. With a fourth-order method, a relatively coarse mesh with one million degrees-of-freedom is able to accurately capture the transition location, the position of separation and reattachment, as well as the average pressure and skin friction coefficient profiles along the foil. The pressure and skin friction coefficients can be seen in the figures below; comparison curves with the data by Galbraith and Visbal [5] and with XFoil [4] are also shown.

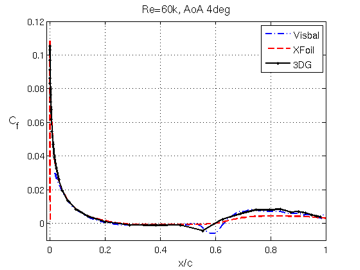
Temporal animations

• Span-wise vorticity at the wing's middle-plane: Reynolds 10,000
  

[ click here if you cannot see the embedded movie above ]

• Span-wise vorticity at the wing's middle-plane: Reynolds 60,000
  

[ click here if you cannot see the embedded movie above ]

• Iso-surfaces of span-wise vorticity at Reynolds 60,000
  

[ click here if you cannot see the embedded movie above ]

• Iso-surfaces of q-criterion at Reynolds 60,000
  

[ click here if you cannot see the embedded movie above ]

• Streamlines at Reynolds 60,000
  

[ click here if you cannot see the embedded movie above ]

• Fluctuations in pressure coefficient (acoustic field) at Reynolds 60,000
  

[ click here if you cannot see the embedded movie above ]

References

[1] R. Alexander, "Diagonally Implicit Runge-Kutta methods for stiff O.D.E.'s", SIAM J. Numer. Anal., Vol. 14, No. 6, pp. 1006-1021, 1978.

[2] F. Bassi and S. Rebay, "A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations", J. Comput. Phys., Vol. 131, pp. 267-279, 1997.

[3] B. Cockburn and C.-W. Shu, "The local discontinuous Galerkin method for time-dependent convection-diffusion systems, SIAM J. Numer. Anal., Vol. 35, No. 6, pp. 2440-2463, 1998.

[4] M. Drela, XFOIL Users Guide, Version 6.94, MIT Aeronautics and Astronautics Department, 2002.

[5] M. Galbraith and M. Visbal, "Implicit Large Eddy Simulation of low Reynolds number flow past the SD7003 airfoil", 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, AIAA paper 2008-225, Jan. 2008.

[6] M. Ol, B. McAuliffe, E. Hanff, U. Scholz, and C. Kahler, "Comparison of laminar separation bubble measurements on a low Reynolds number airfoil in three Facilities", 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, Ontario, Canada, AIAA paper 2005-5149, June 2005.

[7] J. Peraire and P.-O. Persson, "The Compact Discontinuous Galerkin (CDG) Method for Elliptic Problems", SIAM J. Sci. Comput., Vol. 30, No. 4, pp. 1806-1824, 2008.

[8] P.-O. Persson and J. Peraire, " An efficient low memory implicit Discontinuous Galerkin algorithm for time dependent problems", 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, AIAA paper 2006-0113, Jan. 2006.

[9] P.L. Roe, "Approximate Riemann solvers, parameter vectors, and difference schemes", J. Comput. Phys., 43, 1981.

Last updated May 14, 2013.