Principal Stresses

Entity names: P1, P2, P3, worstPS

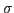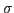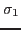
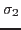
The principal stresses $\sigma$ are named P1, P2, P3. From the three principal stresses $\sigma$ the absolute maximum value will be calculated and named worstPS. For example if a node has the three values 100, 0 and -110 MPa then -110 MPa would be shown. The three principal stresses 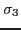$\sigma_{1}$ $\sigma_{2}$ $\sigma_{3}$ are derived from the following equation:

$$\left [ \begin{array}{ccc} \sigma_{xx}-\lambda & \sigma_{xy}... ... ] = \left [ \begin{array}{c} 0\\ 0\\ 0 \end{array}\right ]$$

They are given by the three roots of the equation (stress tensor is symmetric: 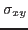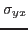$\sigma_{xy}$ = $\sigma_{yx}$ etc.):

$$\sigma^3 - (\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\sigma^2 + (\... ...\sigma_{zz}+\sigma_{zz}\sigma_{xx}-\sigma_{xy}^2-\sigma_{yz}^2-$$

$$\sigma_{zx}^2)\sigma - (\sigma_{xx}\sigma_{yy}\sigma_{zz}+2\s... ..._{yz}^2-\sigma_{yy}\sigma_{zx}^2-\sigma_{zz}\sigma_{xy}^2) = 0$$