







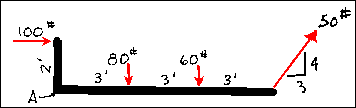
 Given:
Given:
Solution:
The first step is to determine a convenient location for the center of moments. This point should be chosen with care since it can make the problem much easier if correctly chosen. Assume that point A shall be taken as the center of moments. Next, inspect the forces in order to find any that must be decomposed into their components. Only the 50 pound force must be decomposed into its orthagonal components. It has a line of action that is a 3-4-5 triangle. This can be clearly seen by observation. Thus, the components are Fx = 30 pounds and Fy = 40pounds.
Next, find the magnitude and direction of the resultant by summing the moments of the forces and/or their components.
Next, the direction must be determined.
Then, sum of the moments around point A to find the location of the resultant. Assume that the resultant acts along the long side of the crooked arm so that Fx will cause a zero moment.
Sum MA
Therefore, the resultant equals 164 pounds acting 37.4 degrees below the x axis, down and to the right at a point 4.4 feet to the right of point A.