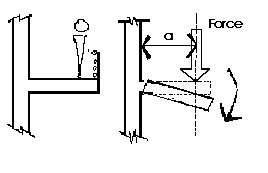
The Moment of a force is a measure of its tendency to cause a body to rotate about a specific point or axis. This is different from the tendency for a body to move, or translate, in the direction of the force. In order for a moment to develop, the force must act upon the body in such a manner that the body would begin to twist. This occurs every time a force is applied so that it does not pass through the centroid of the body. A moment is due to a force not having an equal and opposite force directly along it's line of action.
Imagine two people pushing on a door at the doorknob from opposite sides. If both of them are pushing with an equal force then there is a state of equilibrium. If one of them would suddenly jump back from the door, the push of the other person would no longer have any opposition and the door would swing away. The person who was still pushing on the door created a moment.
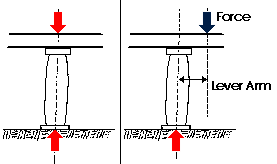
The magnitude of the moment of a force acting about a point or axis is directly proportinoal to the distance of the force from the point or axis. It is defined as the product of the force (F) and the moment arm (d). The moment arm or lever arm is the perpendicular distance between the line of action of the force and the center of moments. The Center of Moments may be the actual point about which the force causes rotation. It may also be a reference point or axis about which the force may be considered as causing rotation. It does not matter as long as a specific point is always taken as the reference point. The latter case is much more common situation in structural design problems. A moment is expressed in units of foot-pounds, kip-feet, newton-meters, or kilonewton-meters. A moment also has a sense; it is either clockwise or counter-clockwise. The most common way to express a moment is
M = F x d
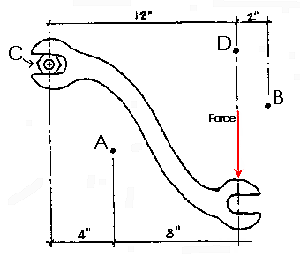
The example shown is a wrench on a nut (at C) that has a force applied to it. The force is applied at a distance of 12 inches from the nut. The center of moments could be point C or points A or B. The moment arm for calculating the moment around point C is 12 inches. The magnitude of the moment of the 100 pound force about point C is 12 inches multiplied by the force of 100 pounds to give a moment of 1200 inch-pounds (or 100 foot-pounds). Similarly, the moment about point A can be found to be 800 inch-pounds.
The direction of the rotation is important to understand in order to describe its effect on the body (structure). A moment will cause either a clockwise or counter-clockwise rotation about the center of moments. It is essential that the direction of rotation about the center of moments be understood. Since an international convention does not exist, in this course, a clockwise rotation about the center of moments will be considered as positive; a counter-clockwise rotation about the center of moments will be considered as negative.
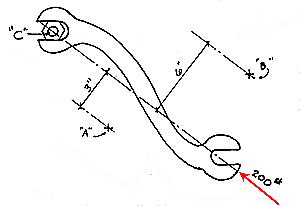
A moment causes a rotation about a point or axis. Thus, the moment of a force taken about any point that lies on its own line of action is zero. Such a force cannot cause a rotation because the moment arm is non-existant.
In this second example, a 200 pound force is applied to the wrench. The moment of the 200 pound force applied at C is zero because 200 pounds x 0 inches = 0 inch-pounds (Fxd = M). In other words, there is no tendency for the 200 pound force to cause the wrench to rotate the nut. One could increase the magnitude of the force until the bolt finally broke off.
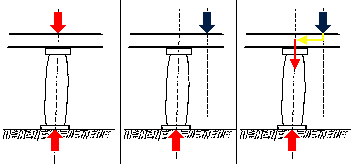
A moment can also be considered to be the result of forces detouring from a direct line drawn between the point of loading of a system and its supports. In this case, the blue force is an eccentric force. In order for it to reach the base of the column, it must make a detour through the beam. The greater the detour, the greater the moment. The most efficient structural systems have the least amount of detours possible. This will be discussed in more detail in Lecture 37 and later courses.
There are cases in which it is easier to calculate the moments of the componenets of a force around a certain point than it is to calculate the moment of the force itself. It could be that the determination of the perpendicular distance of the force is more difficult than determining the perpendicular distance of components of the force. The moment of several forces about a point is simply the algebraic sum of their component moments about the same point. When adding the moments of componenets, one must take great care to be consistant with the sense of each moment. It is often prudent to note the sense next to the moment when undertaking such problems.
Combined Moments
Moments on a Beam
Any difficulty with calculating a moment can usually be traced to one of the following: