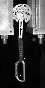
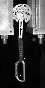 |
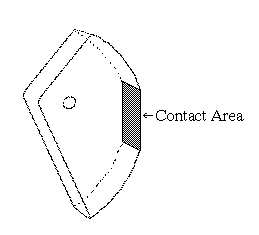
Spring loaded camming devices (SLCDs) are a type of anchor that rock climbers use to connect themselves to cracks or other irregularies in a rock cliff. These devices work through a combination of the wedge principle and friction: once the cams are placed in a crack, any force pulling the cams down causes the cams to press tightly against the crack walls, generating a frictional force that retards the downward pull. Figure 1 (80K) shows a typical SLCD placed in a test fixture crack. Springs built into the device (not visible) keep the cams snug against the walls. Any downward load applied at the carabiner rotates the cams and forces them against the walls, effectively wedging the device more tightly in place. Over the past two decades, SLCDs have proven to be an effective anchor, and now SLCDs are manufactured in a variety of sizes, shapes, configurations, and constructions.
The current methods of testing the spectrum of available SLCDs are
based either on anecdotal evidence that lacks an experimental control
or on pull-to-failure tests that determine the maximum force
obtainable before the device collapses. Such tests provide neither a
full nor accurate picture of a device's holding ability. As a first step
toward developing better methods for the testing of SLCDs, this
report develops a mathematical model for how SLCDs work, suggests
theoretical limitations of SLCD performance determined by the model,
shows preliminary verification of this model, and suggests
implications for both cam testing and the use of SLCDs.
These models are developed for the condition shown in Figure 1, an SLCD subject to a downward
applied force while placed in a vertical, parallel crack. The
parallel crack constraint is chosen for two reasons. From the point
of view of the climber, any evaluation of these devices must address
performance in parallel cracks because SLCDs are designed explicitly
for use in such a situation. The parallel crack criterion is also
important because it bounds narrowing and flaring cracks; parallel
crack results define a performance limit for each regime.
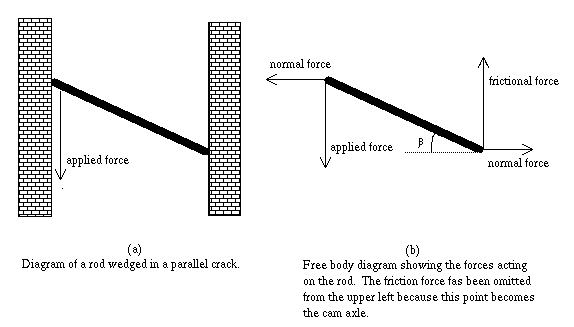
As a first approximation, a camming device can be modeled as a rod
wedged or ``cammed'' in a parallel crack as shown in Figure 2a below. If the rod does not slip out, a
downward tug or force applied to the upper end wedges the rod harder
into the crack, causing the rod to push against the walls with a
normal force. Whether or not the rod slips out is determined by a
third force, that of friction. Figure 2b shows
the forces on the rod; the friction force on the upper left end of the
rod is intentionally omitted. For camming devices that rely on
friction, this upper left end corresponds to an internal axle (see Figure 1 or Figure 4) and
thus experiences negligible friction.
If the rod shown in Figure 2 does not move, both the forces and
torques must each sum to zero. These equalities and the definition of
the friction force yield four equations that define the relation
between the applied, normal and friction forces. R is the rod
length,
Two important results are derived from algebraic manipulation of these
equations:
Equation 1 shows the wedging effect that multiplies the applied force
by a factor of
To produce a camming device that works over a wide range of crack
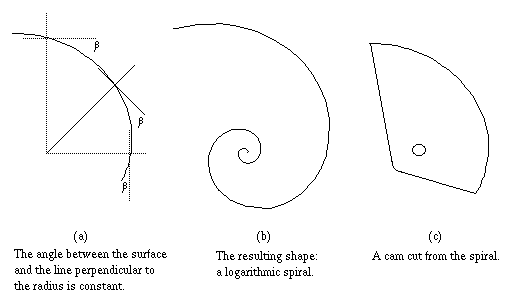
sizes, multiple rods are combined into a two dimensional surface in
the shape of a cam. This shape satisfies the criterion shown in Figure 3a below: the angle between the surface and
the line perpendicular to the radius must remain a constant, the
camming angle,
Rearranging and integrating yields:
Equation 3 defines the logarithmic spiral plotted in
Figure 3b. A section cut from this spiral produces the
cam (Figure 3c). Typically three or four such cams are
mounted together on an axle to produce a complete SLCD.
Modeling SLCDs in Parallel Cracks
A succession of two models is used to develop an understanding of SLCD
performance in parallel cracks. The rigid model assumes that the
actual materials that compose the cams are perfect: perfectly rigid
and strong. This rigid model provides a basic theory of why camming
devices work, defines the cam's shape, and determines the relationship
between the shape and the friction coefficient. The elastic model
builds on the rigid model by additionally taking elasticity and shear
yield into account. The elastic model provides estimates of cam
deformation, the resulting shear loading, and the maximum applied
force to failure.
The Rigid Model -- Explaining How Camming Devices Work
 is the friction coefficient, and
is the friction coefficient, and 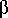 is the
angle the rod makes with the horizontal.
is the
angle the rod makes with the horizontal.
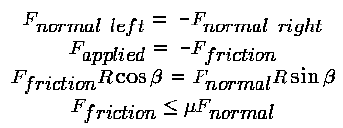
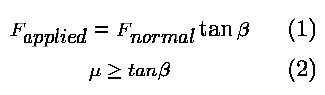
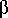 .
.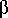 , at which the rod can remain in
the crack is limited by the coefficient of friction,
, at which the rod can remain in
the crack is limited by the coefficient of friction, 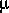 between the rod and the crack surface. For an aluminum rod in a
granite crack, a measured value for the friction coefficient is .38,
and the corresponding maximum camming angle is about 20 degrees; a rod
tipped more than 20 degrees from horizontal would slip out of a
granite crack.
between the rod and the crack surface. For an aluminum rod in a
granite crack, a measured value for the friction coefficient is .38,
and the corresponding maximum camming angle is about 20 degrees; a rod
tipped more than 20 degrees from horizontal would slip out of a
granite crack. 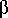 . In polar coordinates, such a shape is defined by:
. In polar coordinates, such a shape is defined by:
![]()
![]()
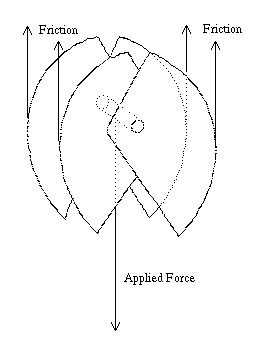 |
Figure 4 shows the forces on a complete SLCD in a parallel crack. The
free body diagram is very similar to the rod in Figure
2, though now the contact forces are spread out evenly over all
four cams. The camming angle is set by the tightness of the spiral
rather than by the rod length and crack width. The relationship
between the camming angle and the friction coefficient is still
determined by Equation 2: any given cam can only hold if tan
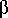 <
< 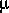 . If the friction coefficient
between the cam and the rock surface drops below tan
. If the friction coefficient
between the cam and the rock surface drops below tan 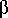 ,
the device fails due to a lack of frictional holding ability.
,
the device fails due to a lack of frictional holding ability.
The Elastic Model -- Materials Failure Modes
 |
Because this equation is derived for cylinders, it only approximates
the deformations of cams. Five simplifications may not reflect actual
cam geometries:
An approximate size of this contact area can be obtained by applying
Hertz's theory2 of the contact between
two elastic bodies.
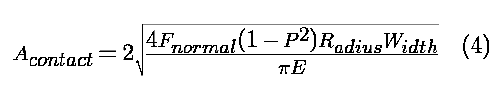
Given these simplifications, Equation 4
approximates the relationship between the applied force, the geometry,
and the material properties: the contact area is proportional to the
square root of the compression force, the radius, and the width.
While the resulting area is not exact, Equation 4 can be used to
estimate the shear stress that develops at the contact area.
Given the contact area from Equation 4, the shear stress at the
cam/crack boundary is approximately
These estimates do not necessarily reflect actual performance; rather,
the force estimates are plotted to show the wide range of maximum
forces that devices might be expected to sustain. These force
estimates span the range of forces that climbers generate. The
highest force that a climber can expect is about 12,000N and a climber
hanging from an anchor applies a force of about 1500N. According to
the elastic model, larger SLCDs can sustain larger forces and the
smaller devices are expected to fail under conditions commonly
experienced by climbers. Even though several estimations and
simplifications are incorporated into the elastic model, the range of
performance expectations remains large. The lower end of the applied
force range is of particular importance because the smaller devices may
fail under nominal conditions.
The perfect SLCD is light weight and durable, fits in a wide range of
crack sizes, anchors reliably to the most slippery rock, has a narrow
profile (width) that allows placement in shallow cracks, and can
sustain the largest applied forces a falling climber can exert. These
optimal characteristics can only be obtained through variation of the
cam's geometry and material properties: the camming angle, radius,
width, Young's Modulus, Poisson's Ratio, and the shear yield. Every
cam is a compromise; efforts to lighten or narrow the cam reduce both
durability and maximum load, and greater range is traded for less
frictional holding ability. These compromises are implicit in
Equation 2, which constrains the camming angle to
be less than the arctan of the friction coefficient, and
Equation 5, which defines the maximum load that can be
applied before the onset of shear failure. Even though these
equations provide only estimates of cam performance, the model
predicts both the wide variation of performance among different SLCDs
and the likelihood that some SLCDs, especially smaller ones, fail at
forces commonly produced by falling climbers.
Published measurements of force to shear yield and frictional holding
ability would provide information that allows climbers to make
intelligent decisions concerning SLCDs. Most importantly, climbers
would be aware when devices have dangerously low frictional holding
ability or maximum load to shear failure. Of similar importance, an
explicit awareness of cam limitations allows climbers to place the
devices more securely and with greater confidence. Finally,
performance information would provide climbers with a way of comparing
SLCDs made by different manufacturers. To date, this information is
either not explicitly stated or simply not available to the climbing
community. Making performance information available would alert
climbers to the existence of SLCD limitations and provide climbers
with the information required to successfully work around these
limitations.
2
from Ball and Roller Bearings, Eschmann, Hasbargen, Weigand, J
Wiley and Sons, pg 113.
3
The literature suggests that the effect of the non-compressive force
is small (Contact Mechanics, KL Johnson, Cambridge University
Press, 1985).
4
Finite element analysis work by Luke Sosnowski suggests a negligible
difference between logarithmic and circular curvature.
5
Ball and Roller Bearings, Eschmann, Hasbargen, Weigand, J Wiley
and Sons, pg 118.
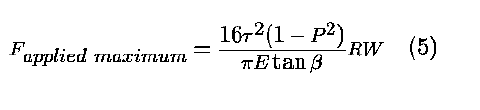
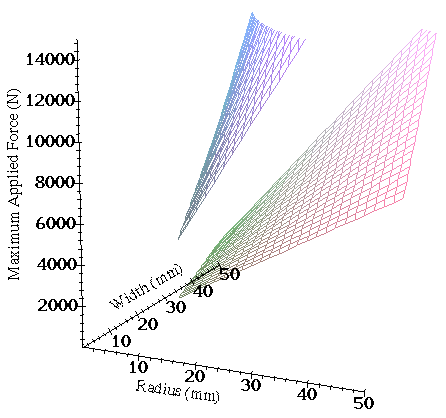
Figure 6: Estimated maximum applied force
sustainable for two types of SLCDs.
Footnotes
![]() Dave Custer's home page
Dave Custer's home page