Spreading Behavior of Molten Metal Microdroplets
by
Ho-Young Kim
B. S., Mechanical Engineering, Seoul National University (1994)
S. M., Mechanical Engineering, Massachusetts Institute of Technology
(1996)
Submitted to the Department of Mechanical Engineering
in Partial Fulfillment of the Requirements for the Degree of
DOCTOR OF PHILOSOPHY IN MECHANICAL ENGINEERING
at the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
February 1999
© 1999 Massachusetts Institute of Technology
All Rights Reserved
Signature of Author:
Department of Mechanical Engineering
February 3, 1999
Certified by:
Jung-Hoon Chun
Associate Professor of Mechanical Engineering
Chairman, Doctoral Thesis Committee
Accepted by:
Ain A. Sonin
Professor of Mechanical Engineering
Chairman, Department Graduate Committee
Spreading Behavior of Molten Metal Microdroplets
by
Ho-Young Kim
Submitted to the Department of Mechanical Engineering
on February 3, 1999 in Partial Fulfillment of the Requirements
for the Degree of
Doctor of Philosophy in Mechanical Engineering
ABSTRACT
Deposition of molten microdroplets is fundamental to many emerging
technologies, such as the Droplet-Based Manufacturing (DBM) process. Although
the spreading behavior of ordinary liquid and molten droplets have been
studied extensively for many years, some basic questions remain unanswered.
Specifically, to determine the optimal deposition conditions for the DBM
process, it is essential to understand the fundamental mechanisms behind
abnormal spreading behavior, such as splashing and bouncing. In this thesis,
the fundamental, but still poorly understood, behavior of the liquid and
molten metal droplets upon colliding with solid surfaces is investigated.
As the first problem, the splashing of liquid droplets is addressed.
A linear perturbation theory is developed for the interface instabilities
of a radially-expanding, liquid sheet in cylindrical geometries. The theory
is then applied to rapidly spreading droplets as the fundamental mechanism
behind splashing. The effects of such factors as the transient profile
of the interface radius, the perturbation onset time, and the Weber number
on the analysis results are examined. The analysis shows that the wave
number of maximum instability does not remain constant but rather, changes
during spreading because of time-dependent coefficients in the amplitude
equation. It is also found that large impact inertia, associated with a
high Weber number, promotes interface instability and that prefers high
wave number for maximum instability.
In the next stage of research, the oscillations of liquid droplets
upon colliding with solid surfaces are investigated as a prerequisite for
the understanding of droplet bouncing. Experiments using a high speed video
system show that the droplets with higher impact inertia oscillate more
vigorously upon colliding with a solid surface. The oscillation is strongly
affected by the wetting between the liquid droplet and the solid surface,
such that the oscillation is greatly promoted in poor wetting conditions.
In addition, approximate models based on the variational principle, rather
than the Navier-Stokes equation, are developed in this thesis. The results
of the models are in good agreement with experimental data. In addition,
the analysis shows that the relative magnitudes of surface energy and viscous
dissipation play critical roles in determining droplet dynamics. Significant
computational effort is saved by the models which solve a single second
order, nonlinear differential equation.
Following the study of the oscillations, the bouncing of molten
metal droplets upon colliding with subcooled target surfaces is studied.
To determine the conditions for bouncing and sticking, an empirical regime
map is constructed using an approximate model and extensive experimental
data. A clear trend develops, illustrating that bouncing occurs when solidification
is slow compared to oscillation, when a molten metal droplet collides with
a nonwetting surface. It is also found that bouncing is prohibited by good
wetting between the droplet and the target, which suggests that the wetting
be an additional parameter which may affect the bouncing behavior.
Thesis Supervisor: Dr. Jung-Hoon Chun
Title: Associate Professor of Mechanical Engineering
Acknowledgments
Table of Contents
Title Page 1
Abstract 2
Acknowledgments 3
Table of Contents 4
List of Tables 6
List of Figures 7
CHAPTER 1 INTRODUCTION 2
1.1. General background 2
1.2. Scope of the present investigation 3
1.3. Organization of thesis 4
CHAPTER 2 SPLASHING OF LIQUID DROPLETS UPON COLLIDING
WITH SOLID SURFACES 5
2.1. Introduction 5
2.2. Derivation of the amplitude equation 7
2.3. Numerical simulation results 11
2.4. Conclusions 13
CHAPTER 3 THE OSCILLATIONS OF LIQUID DROPLETS UPON
COLLIDING WITH SOLID SURFACES 25
3.1. Introduction 25
3.2. Modeling 26
3.2.1. Formulation of the problem using a cylinder
model 27
3.2.2. Formulation of the problem using a truncated
sphere model 31
3.3. Description of the experimental apparatus 33
3.4. Experimental and modeling results 34
3.5. Discussions and conclusions 36
CHAPTER 4 BOUNCING OF MOLTEN METAL DROPLET UPON
COLLIDING WITH SOLID SURFACES 58
4.1. Introduction 58
4.2. Description of the experimental apparatus 58
4.3. Results and discussion 59
4.3.1. Experimental observations 60
4.3.2. An approximate model 60
4.3.3. Regime map of droplet boucing 62
4.5. Conclusions 63
CHAPTER 5 CONCLUSIONS 74
BIBLIOGRAPHY 76
APPENDICES 82
APPENDIX A. NONDIMENSIONAL QUANTITIES 82
APPENDIX B. FREQUENCY OF PERTURBATIONS TO A CONSTANT
RADIUS LIQUID SHEET 83
APPENDIX D. MEASUREMENT OF EQUILIBRIUM CONTACT ANGLES
84
List of Tables
TABLE 3.1. Physical properties of the liquids used
in the experiments 39
TABLE 3.2. Dissipation factors 39
TABLE D.1. Equilibrium contact angles 85
List of Figures
FIGURE 2.1. Release of a liquid sheet upon the droplet
collision with a solid target. 15
FIGURE 2.2. Disturbed liquid sheet which expands
radially. 15
FIGURE 2.3. Limiting cases of droplet spreading.
The original droplet radius and velocity are both unity after nondimensionalization.
(a) Volume 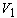 is
displaced to
is
displaced to 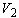 while the droplet descends with the speed of unity. The cylinder radius
while the droplet descends with the speed of unity. The cylinder radius 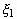 is expressed as Eq. (23). (b)
is expressed as Eq. (23). (b) 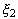 is the intersection radius of the target surface and the droplet traveling
with no deformation. 16
is the intersection radius of the target surface and the droplet traveling
with no deformation. 16
FIGURE 2.4. (a) Transient radius profiles of an expanding
liquid sheet expressed as 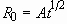 .
(b) Corresponding deceleration. Note that the significant deceleration
is experienced by the interface immediately after impact, which drives
the Rayleigh-Taylor instability. 17
.
(b) Corresponding deceleration. Note that the significant deceleration
is experienced by the interface immediately after impact, which drives
the Rayleigh-Taylor instability. 17
FIGURE 2.5. The coefficients of Eq. (23) when 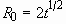 and
and 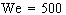 . (a) The
coefficient a is given by
. (a) The
coefficient a is given by 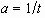 .
(b) The coefficient b vs. time for various wave numbers. 18
.
(b) The coefficient b vs. time for various wave numbers. 18
FIGURE 2.6. (a) Temporal evolution of the shape amplitudes
of various wave numbers until 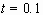 .
(b) Temporal evolution of the shape amplitudes until
.
(b) Temporal evolution of the shape amplitudes until 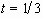 .
Initial conditions at
.
Initial conditions at 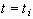 are
are 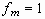 and
and 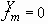 .
The computation was performed for
.
The computation was performed for 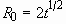 ,
, 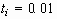 ,
and
,
and 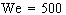 . Perturbations
of
. Perturbations
of 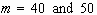 are exceeded
by that of
are exceeded
by that of 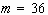 during
spreading. Perturbations of
during
spreading. Perturbations of 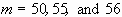 decay after initially growing period. The perturbation amplitude of
decay after initially growing period. The perturbation amplitude of 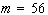 even decays to the value less than the initially assigned one before t
reaches
even decays to the value less than the initially assigned one before t
reaches 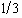 . We define
a wave number, which is less than the so-found wave number by one, as a
pseudo-cutoff wave number - in this case, it is 55. 19
. We define
a wave number, which is less than the so-found wave number by one, as a
pseudo-cutoff wave number - in this case, it is 55. 19
FIGURE 2.7. (a) Perturbation amplitude vs. wave numbers
for different time. Initial conditions for solid lines are 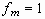 and
and 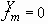 . Initial
conditions for a dotted line are
. Initial
conditions for a dotted line are 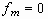 and
and 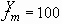 . The computation
was performed for
. The computation
was performed for 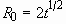 ,
, 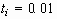 ,
and
,
and 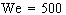 . (b) Changes
of a mode number of maximum instability and a pseudo-cutoff wave number
with time. Computation conditions are those of the solid lines in (a).
(c) Growth of azimuthal disturbances during spreading at the modes of maximum
instability. From the innermost corrugated circle,
. (b) Changes
of a mode number of maximum instability and a pseudo-cutoff wave number
with time. Computation conditions are those of the solid lines in (a).
(c) Growth of azimuthal disturbances during spreading at the modes of maximum
instability. From the innermost corrugated circle, 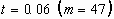 ,
, 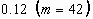 ,
, 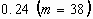 ,
and
,
and 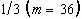 . Initial
conditions are
. Initial
conditions are 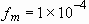 and
and 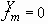 . The other
conditions are identical to those of (a). 20
. The other
conditions are identical to those of (a). 20
FIGURE 2.8. Effect of the coefficient A on instability.
(a) Wave number of maximum instability vs. A. (b) Perturbation amplitude
of those numbers vs. A. 22
FIGURE 2.9. Effect of the perturbation onset time 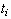 on instability. (a) Wave number of maximum instability vs.
on instability. (a) Wave number of maximum instability vs. 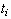 .
(b) Perturbation amplitude of those numbers vs.
.
(b) Perturbation amplitude of those numbers vs. 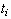 .
23
.
23
FIGURE 2.10. Effect of Weber number on instability.
(a) Wave number of maximum instability vs. We. (b) Perturbation amplitude
of those numbers vs. We. 24
FIGURE 3.1. Geometry of the cylinder model 40
FIGURE 3.2. Initial diameter and height of the cylinder
versus contact angle as given by Eq. (3.24) and (3.4) 41
FIGURE 3.3. Geometry of the truncated sphere model
42
FIGURE 3.4. Experimental apparatus for the high speed
imaging of the droplet oscillations 43
FIGURE 3.5. Images of a water droplet colliding with
acrylic surface. (a) Original droplet diameter = 3.6 mm, Impact velocity
= 0.77 m/s, We=30, Re=3214. (b) Original droplet diameter = 3.5 mm, Impact
velocity = 3.47 m/s, We=582, Re=13850. 44
FIGURE 3.6. The temporal evolution of the base diameter
of water droplets colliding with acrylic surface. The impact conditions
for triangles and squares are the same as the FIG. 3.5 (a) and (b), respectively.
The impact conditions for circles 47
FIGURE 3.7. Predictions of the models and the experimental
measurements for water droplets on acrylic surface. Modeling results using
the truncated sphere model and the cylinder model are presented. In the
cylinder model, two different initial base diameters can be used as shown
in Fig. 3."D0 and h0 vs. theta", and both the results are shown. 48
FIGURE 3.8. Effect of target surfaces on droplet
dynamics. (a) Water droplet on acrylic and silicon oxide. (b) Ink droplet
on acrylic and silicon oxide. 49
FIGURE 3.9. Images of a ink droplet colliding with
acrylic surface. Original droplet diameter = 3.2 mm, Impact velocity =
1.75 m/s, We=190, Re=2296. 50
FIGURE 3.10. (a) Dynamic behavior of water, ink,
and silicone oil droplets colliding with the acrylic surface. (b) Dynamic
behavior of water, and ink droplets colliding with the silicon oxide surface.
52
FIGURE 3.11. Images of a silicone oil droplet colliding
with acrylic surface. Original droplet diameter = 2.8 mm, Impact velocity
= 1.44 m/s, We=166, Re=118. 53
FIGURE 3.12. (a) Effect of the Weber number. (b)
Effect of the Reynolds number. (c) Effect of the contact angle. 55
FIGURE 3.13. Necking of a rising water column during
a recoiling process. 56
FIGURE 4.1. Experimental apparatus for the high speed
imaging of molten droplet impact. 65
FIGURE 4.3. (a) Images of molten tin droplets arrested
by solidification upon colliding with the aluminum 6061 surface. Original
droplet diameter = 1.57 mm, Impact velocity = 3.04 m/s, Droplet temperature
at impact = 261?C, Target temperature = 30?C. (b) Images of molten tin
droplets bouncing off the stainless steel 304 surface. Original droplet
diameter = 1.67 mm, Impact velocity = 3.08 m/s, Droplet temperature at
impact = 263?C, Target temperature = 195?C. (c) Images of molten tin droplets
colliding with the stainless steel 304 surface, showing the transitional
behavior. Original droplet diameter = 1.40 mm, Impact velocity = 2.91 m/s,
Droplet temperature at impact = 257?C, Target temperature = 183?C. 66
FIGURE 4.4. Micro tin droplets deposited on stainless
steel targets. 70
FIGURE 4.5. Micro tin droplets deposited on solid
tin targets. 71
FIGURE 4.6. Geometry and temperature profile of the
solidification model. 72
FIGURE 4.7. (a) Regime map of bouncing and sticking
on nonwetting surfaces. Squares and circles denote bouncing and sticking,
respectively. The slope is for the straight line in the linear scale. (b)
Sticking of tin droplets on tin targets. 73
FIGURE D.1. Geometry of a sessile droplet of the
spherical cap shape 85
CHAPTER 1
INTRODUCTION
1.1. General background
The deposition of molten metal droplets plays an important role
in many emerging fields of technology, such as spray forming, spray coating,
rapid prototyping, and electronic packaging. Deposition phenomena comprise
the impact of individual droplets on substrates, coalescence of adjacent
splats after impact, bonding between droplets and the deposit, and microstructural
evolution of a sprayed deposit. The impact and spreading behavior of each
droplet are crucial to the overall deposition process, for they govern
the subsequent processes. Accurate understanding and control of droplet
deposition is essential since it determines geometric definition, such
as surface porosity and conformity to the target shapes, and mechanical
properties of deposit. Although extensive research on the spreading behavior
of molten metal droplets has been performed so far (Madejski 1976; McPherson
1981; Liu et al. 1995; Pasandideh-Fard et al. 1998; Xiong et al. 1998),
complicated physical phenomena involved in the subject have rendered serious
difficulties in understanding the problem. The difficulties mainly arise
from the inherently coupled nature of fluid motion and cooling.
Describing the motion of a spreading droplet requires solving the
moving boundary problem for the Navier-Stokes equation, which is known
to be notoriously difficult (Mei 199?). Furthermore, the contact between
a liquid droplet and a solid surface demands consideration of the physics
of wetting, of which complete understanding is still beyond our ability
(de Gennes 1985). Due to scientific interests on the subject as well as
its practical applications, the spreading behavior of ordinary liquid droplets
without solidification has also been studied extensively for many years
(Worthington 1877a,b; Engel 1955; Bechtel et al. 1981; Stow and Hadfield
1981; Chandra and Avedisian 1991; Pasandideh-Fard et al. 1996). Regardless
of the degree of solidification during spreading, the fluid motion is fundamental
to understanding molten metal impact behavior. Moreover, at the limit when
solidification is much slower than the fluid motion, the treatment of our
problem is identical to that of ordinary liquid droplets (Trapaga and Szekely
1991; Bennett and Poulikakos 1993).
Nonetheless, the description of dynamics of molten metal droplets
deposited on subcooled (colder than the melting point of the droplet material)
target surfaces involve solidification in addition to fluid motion. Approximate
but analytical approaches to the simultaneous effects of solidification
and fluid flow in spreading droplets were taken by Madejski (1976) and
Solonenko et al. (1994). However, the majority of past modeling efforts
employed computational methods due to the complexity of the phenomenon.
The full Navier-Stokes equation and the Stefan problem of solidification
were simultaneously solved by Liu et al. (1993), San Marchi et al. (1993),
and Liu et al. (1994). Trapaga et al. (1992), Waldvogel and Poulikakos
(1997), and Pasandideh-Fard et al. (1998) solved the two-dimensional energy
equation, instead of the Stefan problem, with the Navier-Stokes equation.
In addition to the modeling efforts, experimental studies were carried
out on the behavior of impacting droplets (Inada 1988; Watanabe et al.
1992; Inada and Yang 1994; Schiaffino 1996). The experiments showed that
although the effects of solidification are negligible in the initial stages
of rapid spreading, in the later stages, solidification arrests the fringe
of the impacting droplet and also interacts with the droplet oscillations.
1.2. Scope of the present investigation
Most spray-deposition processes desire to achieve the deposition
of droplets in a controlled and precise manner. Therefore, the mechanisms
behind abnormal impact behavior such as splashing and bouncing must be
understood to produce high-quality deposits. Splashing increases the bulk
and surface porosity of a deposit and consequently deteriorates its quality.
Furthermore, a high degree of splashing worsens the sticking efficiency
of the spray-deposition process, decreasing process yield. It is highly
possible that the droplets which tend to oscillate vigorously have poor
contact with the substrate, which hinders rapid solidification consequently.
In addition, the deposition of an individual molten microdroplet for the
electronic packaging demands a thorough understanding of the droplet oscillations
to prevent droplet bouncing and to predict the final bump shape.
Using dimensional analysis, we can obtain the independent parameters
which affect the spreading behavior of droplets. In the case of isothermal
deposition, neglecting gravity effects, we find the following relevant
scaling parameters: Weber number, Ohnesorge number, and additional parameter(s)
determined by the interfacial phenomena between the droplet liquid and
target solid. The Weber number, We, is the ratio of inertial to surface
tension forces at impact, and the Ohnesorge number, Oh, is the ratio of
viscous to surface tension forces. We assume that only the equilibrium
contact angle, 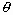 , plays
the dominant role as the interfacial parameter. The Weber number scales
the driving force for the droplet spreading, and the Ohnesorge number scales
the force that resists the spreading (Schiaffino 1996). Schiaffino derived
four different, asymptotic spreading regimes given good wetting conditions.
, plays
the dominant role as the interfacial parameter. The Weber number scales
the driving force for the droplet spreading, and the Ohnesorge number scales
the force that resists the spreading (Schiaffino 1996). Schiaffino derived
four different, asymptotic spreading regimes given good wetting conditions.
Most spray-deposition applications operate in the regime of inviscid,
impact-driven spreading, where We >> 1 and Oh << 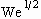 .
The regime is characterized by rapid initial spreading followed by well-pronounced
oscillations. We can subdivide this regime based on the strength of the
spreading and the oscillations. When the driving force of the spreading
is very strong, the droplet develops an unstable spreading front which
leads to splashing. In addition, when the oscillations are very strong,
the droplet may disengage from the target surface, which is referred to
as bouncing, or disintegrate, which is called necking, during recoiling.
.
The regime is characterized by rapid initial spreading followed by well-pronounced
oscillations. We can subdivide this regime based on the strength of the
spreading and the oscillations. When the driving force of the spreading
is very strong, the droplet develops an unstable spreading front which
leads to splashing. In addition, when the oscillations are very strong,
the droplet may disengage from the target surface, which is referred to
as bouncing, or disintegrate, which is called necking, during recoiling.
Therefore, this thesis investigates the droplet dynamics in the
regime of inviscid, impact-driven spreading. We study the initial spreading
stages that possess excessive driving force, to understand the splashing
phenomenon. Following the study of the initial spreading, we investigate
the subsequent oscillation phenomena. In this study, the effects of the
contact angle as well as Weber number and Ohnesorge number are investigated
since wetting plays an important role in the oscillation stages. After
describing the oscillation dynamics, we study the bouncing of molten metal
droplets as an extremely violent form of droplet oscillations. We include
the effects of solidification in the study to explain the strong dependency
of bouncing and sticking behavior on the thermal conditions.
1.3. Organization of thesis
The present chapter describes the background and the scope for
the thesis. In chapter 2, the splashing phenomena of liquid droplets are
studied. Although splashing of liquid droplets upon colliding with solid
surfaces is frequently observed in a variety of situations, the fundamental
mechanism behind it is still not fully understood. The linear perturbation
theory is developed to model the unstable spreading front of a radially
expanding liquid sheet which emerges from a droplet upon colliding with
a solid surface. Chapter 3 describes the oscillation dynamics of various
liquid droplets on different solid surfaces. We experimentally identify
the effects of impact and surface conditions on the spreading and subsequent
oscillations. The experimental data are compared with approximate models.
Following the study of the oscillations, the bouncing of molten metal droplets
upon colliding with subcooled targets is investigated in chapter 4. The
regime map for the bouncing and sticking of the molten metal droplets is
constructed based on experimental results and modeling. Chapter 5 offers
the conclusions of this thesis.
CHAPTER 2
SPLASHING OF LIQUID DROPLETS UPON
COLLIDING WITH SOLID SURFACES
2.1. Introduction
One frequently observes a droplet with large inertia, when it impinges
on a solid surface, spread with fingers extending from the edge. Although
the behavior of a spreading droplet after colliding with a target plane
has been the subject of intense study for many years (Worthington 1877a,b;
Engel 1955; Harlow and Shannon 1967; Bowden and Field 1964; Chandra and
Avedisian 1991; Fukai et al. 1995), comparatively less work has been done
on a splashing droplet - droplet that develops the unstable periphery.
Levin and Hobbs (1971) observed the formation of a
crown, i.e. the detachment of the watersheet from a target surface, when
a water drop impinges on a copper hemisphere. Stow and Hadfield (1981)
photographed the early development of the watersheet emerging from the
drop/target contact area, and were able to distinguish a splashing droplet
from non-splashing ones by the release of an unstable watersheet in the
very early stages of spreading. Mundo et al. (1995) characterized the size
and velocity of the secondary droplets produced from a droplet colliding
with a rotating disc at an angle. Thoroddsen and Sakakibara (1998) first
performed a systematic study on the evolution of the fingers developing
from a droplet interface spreading on a flat glass substrate. Furthermore,
recent experiments (Thoroddsen and Sakakibara 1998; Marmanis and Thoroddsen
1996) showed that the unstable azimuthal undulation is a characteristic
feature of splashing. For this reason, we consider that splashing is the
unstable expansion of the spreading front in colliding droplets, including
crown formation as an extreme case of splashing.
Significant experimental observations of splashing droplets are
summarized as the following: (1) Splashing manifests itself in the very
early stages of spreading. (Stow and Hadfield 1981; Thoroddsen and Sakakibara
1998) (2) It occurs when the impacting droplet has significant kinetic
energy as compared to surface energy and it is promoted by rough target
surfaces (Stow and Hadfield 1981; Mundo et al. 1995) A crown even develops
under severe destabilizing conditions. (3) Increasing the impact inertia
increases the number of fingers (Marmanis and Thoroddsen 1996), and this
number does not change significantly during spreading (Thoroddsen and Sakakibara
1998).
A few articles (Allen 1975; Mundo et al. 1995; Thoroddsen and Sakakibara
1998) have so far paid attention to the origin of
splashing, but the basic mechanism of splashing is still far from clear.
Allen (1975) suggested that a radially decelerating interface of a spreading
droplet be Rayleigh-Taylor unstable and calculated the most dangerous wavelength
based on the average deceleration required to bring the spreading to a
halt. He modeled the radially extending flow into one-directional plane
motion and assumed that the deceleration was due to viscous damping. However,
his model overlooked the effects of a changing interface length during
spreading and the curvature on the instabilities. In addition, the selection
of the representative deceleration is arbitrary to an extent. Mundo et
al. (1995) suggested that the crown develop when the total energy of a
droplet prior to impact exceeds the amount of energy dissipated by viscosity
during spreading. On the other hand, Thoroddsen and Sakakibara (1998) contended
that the fingering is due to the Rayleigh-Taylor instability of the decelerating
fluid ring at the droplet bottom before hitting a target.
To elucidate the fundamental mechanism behind splashing we note
the above experimental observation (1): the behavior of a liquid sheet
released upon impact is crucial in understanding the splashing. In the
present work, we study the Rayleigh-Taylor instability of a radially expanding
sheet, in "cylindrical" geometry, as a major mechanism to induce splashing.
Figure 2.1 shows a sheet that is typically released during impact-driven
spreading.
Although the Rayleigh-Taylor instability has been extensively studied
for many years, most of effort has been focused on the plane (Taylor 1950;
Menikoff et al. 1978; Tryggvason 1988; Berning and Rubenchik 1998) and
spherical geometries (Plesset 1954; Plesset and Mitchell 1956; Birkhoff
1956; Baker et al. 1984). Especially, interests in cavitation bubbles,
pulsations of underwater explosion bubbles, and sonoluminescence (Hilgenfeldt
et al. 1998) have brought attention to the dynamics of spherical bubbles.
Behavior of a gas bubble in an incompressible liquid under adiabatic or
isothermal conditions is described by the Rayleigh-Plesset (RP) equation
(Plesset and Prosperetti 1977; Feng and Leal 1997). The distortion amplitude
of the spherical interface is governed by an equation whose coefficients
are time-dependent as ruled by the RP equation. When the amplitude of the
radial oscillation is small, the governing equations for the shape modes
are reduced to Mathieu's equation. On the other hand, Brenner et al. (1995)
examined both the Rayleigh-Taylor and the parametric instability mechanisms
for a large amplitude case. Generally, numerical methods are required to
understand such a case.
In the present work, we investigate instabilities of a radially-expanding
circular interface in cylindrical geometries. While the bubble dynamics
are governed by the RP equation, the motion of the liquid sheet of our
interest is ruled by the dynamics of droplet spreading. Since the details
of initial droplet spreading stages are not precisely known, we build a
simple model on the expansion of a liquid sheet upon impact. It is assumed
that the deceleration of the sheet interface is due to a mass-conservation
controlled flow characteristic rather than viscous damping. An equation
governing the azimuthal instability of an expanding sheet is obtained using
domain perturbation methods. The dynamic conditions of a droplet prior
to impact is represented by Weber number in our analysis. The sensitivity
of the instability analysis to the modeling assumptions and the role of
impact conditions are investigated using numerical simulation.
2.2. Derivation of the amplitude equation
Consider a radially-expanding liquid sheet whose expansion rate,
i.e. radial velocity as a function of time, is known a priori. Stability
of the edge of the two-dimensional, liquid sheet subjected to an azimuthal
disturbance is investigated. Without disturbance, its shape is given only
by time, and the velocity is determined merely by time and radial distance.
However, under the azimuthal disturbance the location of the periphery
is, as shown in Fig. 2.2, dependent upon an azimuthal angle 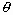 as well as time.
as well as time.
We nondimensionalize the flow parameters based on the characteristic
radius 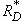 and the characteristic
velocity
and the characteristic
velocity 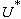 . In the case
of rapidly spreading liquid droplets,
. In the case
of rapidly spreading liquid droplets, 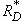 and
and 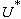 correspond to the
original droplet radius before impact and the impact velocity, respectively.
The characteristic time scale
correspond to the
original droplet radius before impact and the impact velocity, respectively.
The characteristic time scale 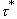 is given by
is given by 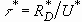 , and the velocity
potential is scaled by
, and the velocity
potential is scaled by 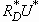 .
Following quantities are all nondimensionalized based on
.
Following quantities are all nondimensionalized based on 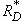 ,
, 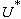 ,
, 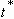 ,
and
,
and 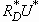 , and their forms are
shown in Appendix A.
, and their forms are
shown in Appendix A.
The velocity potential of the liquid 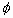 is defined such that the radial velocity
is defined such that the radial velocity 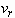 and the azimuthal velocity
and the azimuthal velocity 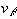 satisfy, respectively,
satisfy, respectively,
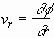 , (2.1)
, (2.1)
and
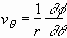 . (2.2)
. (2.2)
It is supposed that the velocity potential and the outer radius
of the fluid R are slightly disturbed, so that they are expressed
as
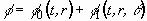 , (2.3)
, (2.3)
and
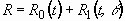 , (2.4)
, (2.4)
where 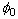 and
and 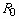 denote the base - axisymmetric spreading - solutions and
denote the base - axisymmetric spreading - solutions and 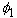 and
and 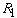 are small perturbations.
We neglect the effect of viscosity, hence the governing equation for incompressible
and irrotational flow is
are small perturbations.
We neglect the effect of viscosity, hence the governing equation for incompressible
and irrotational flow is
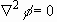 . (2.5)
. (2.5)
We model the axisymmetric liquid expansion by a line source at
the center, thus the base flow solution is given by
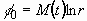 , (2.6)
, (2.6)
where M is the strength of the source. Then the base solution
of the radial velocity is expressed as
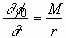 . (2.7)
. (2.7)
Kinematic boundary condition (KBC) at the edge of the expanding
fluid is
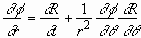 . (2.8)
. (2.8)
Using Eqs. (2.3) and (2.4), we can rewrite KBC as
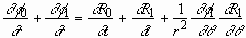 . (2.9)
. (2.9)
It is noted that KBC is imposed on a moving interface at 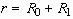 ,
whose location is not known a priori. Therefore, the domain perturbation
method is applied to find a boundary condition which is to be imposed on
an unperturbed interface. From the Taylor series expansion, we obtain the
following expressions which are correct to the first order:
,
whose location is not known a priori. Therefore, the domain perturbation
method is applied to find a boundary condition which is to be imposed on
an unperturbed interface. From the Taylor series expansion, we obtain the
following expressions which are correct to the first order:
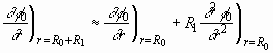 , (2.10)
, (2.10)
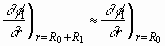 . (2.11)
. (2.11)
Hence KBC to be imposed on 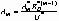 ,
for zeroth order, is
,
for zeroth order, is
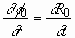 , (2.12)
, (2.12)
and KBC of first order is, using Eq. (2.6),
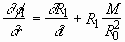 . (2.13)
. (2.13)
In addition, combining Eqs. (2.7) and (2.12), we obtain the following
expressions for M:
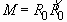 , (2.14)
, (2.14)
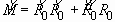 . (2.15)
. (2.15)
Dynamic boundary condition (DBC) on a free surface at 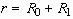 is
is
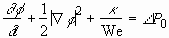 , (2.16)
, (2.16)
where 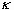 denotes
the curvature of the interface and
denotes
the curvature of the interface and 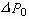 the pressure adjustment. Weber number We is given by
the pressure adjustment. Weber number We is given by 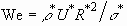 ,
, 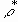 and
and 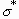 being the density
and the surface tension of the liquid, respectively. The curvature
being the density
and the surface tension of the liquid, respectively. The curvature 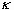 is expressed as, to the first order,
is expressed as, to the first order,
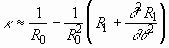 . (2.17)
. (2.17)
Domain perturbation is again applied to DBC to obtain a condition
for the unperturbed interface. DBC to be imposed on 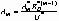 for the first order is
for the first order is
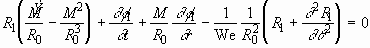 . (2.18)
. (2.18)
As a solution of the Laplace equation, 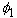 is expressed as a superposition of normal modes:
is expressed as a superposition of normal modes:
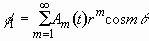 , (2.19)
, (2.19)
where only sinusoidal perturbations were considered. Choosing a
potential which corresponds to a disturbance decreasing away from the interface
in the inward direction (Plesset 1954) has eliminated terms having 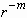 from the solution of the Laplace equation. Consequently, the shape perturbation
is given by
from the solution of the Laplace equation. Consequently, the shape perturbation
is given by
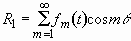 . (2.20)
. (2.20)
Substitution of Eqs. (19) and (20) into Eq. (13) yields
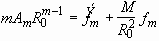 . (2.21)
. (2.21)
Equation (2.18) becomes, after substituting Eqs. (2.19) and (2.20)
in it,
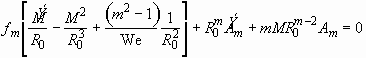 . (2.22)
. (2.22)
Combining Eqs. (2.21) and (2.22), we finally obtain an equation
for the shape perturbation amplitude 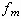 :
:
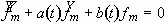 , (2.23)
, (2.23)
where a and b are given as the following, by virtue
of Eqs. (2.14) and (2.15):
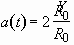 , (2.24)
, (2.24)
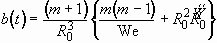 . (2.25)
. (2.25)
In a special case where 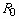 is kept at unity throughout time, the frequency for the mth mode
perturbation,
is kept at unity throughout time, the frequency for the mth mode
perturbation, 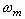 , is given
by
, is given
by
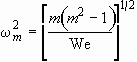 , (2.26)
, (2.26)
which is identical to Chandrasekhar's result (1961). See Appendix
B for the detail.
In short, Eq. (2.23) describes the development of a nonaxisymmetric
perturbation on a cylindrical spreading sheet. The coefficients are known
if the spreading dynamics is known. We note that Eq. (2.23) is a second
order linear ordinary differential equation with variable coefficients.
This equation cannot be solved analytically although stability of the solution
can be obtained for limit cases when the coefficients are periodic functions
of t.
2.3. Numerical simulation results
We begin to investigate the instability by obtaining the base flow
solutions. According to Bowden and Field's model (1964), we expect a nearly
immediate generation of a liquid sheet on impact when Mach number, 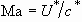 ,
, 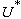 being the impact velocity and
being the impact velocity and 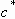 the sound speed in the liquid medium, is very small. However, due to a
lack of quantitative empirical data on the behavior of droplets immediately
after impact, we resort to simple models to obtain the base flow solutions.
In addition, we investigate the sensitivity of the instability to our assumptions.
the sound speed in the liquid medium, is very small. However, due to a
lack of quantitative empirical data on the behavior of droplets immediately
after impact, we resort to simple models to obtain the base flow solutions.
In addition, we investigate the sensitivity of the instability to our assumptions.
To obtain the base flow solution, i.e. the expansion rate of the
liquid sheet or contact area, we consider the following limiting case.
Suppose that the descending speed of a droplet after impact is invariant
from its original speed, which is often observed in the early stages of
spreading (Stow and Hadfield 1981, Thoroddsen and Sakakibara 1998). As
shown in Fig. 2.3 (a), we assume that the bottom of the spherical droplet
is displaced to the periphery of the droplet spreading on the surface,
resulting in a shape of truncated-sphere-on-cylinder. Using volume conservation,
the radius of the cylinder or contact radius is calculated to be
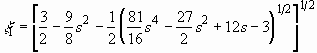 , (2.27)
, (2.27)
where 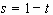 (
(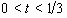 ).
For
).
For 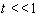 ,
, 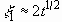 .
It is interesting to note that if the droplet continues to travel after
hitting the surface as if it did not exist (See Fig. 2.3 (b)), the radius
of intersecting area is expressed as
.
It is interesting to note that if the droplet continues to travel after
hitting the surface as if it did not exist (See Fig. 2.3 (b)), the radius
of intersecting area is expressed as 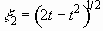 ,
which is approximated to be
,
which is approximated to be 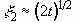 for
for 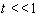 . We suppose that the
expanding liquid sheet exhibits the same tendency as
. We suppose that the
expanding liquid sheet exhibits the same tendency as 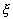 's
modeled above, then we write
's
modeled above, then we write
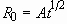 , (2.28)
, (2.28)
where the coefficient A is to be determined empirically
for each impact situation. Figure 2.4 shows radius and deceleration profiles
depending on the value of A.
We predict that in the context of the Rayleigh-Taylor instability,
when the expanding liquid decelerates with respect to a lighter atmospheric
gas, it tends to be destablized while the surface tension has stabilizing
effect. It is also possible to approximately predict the stability by observing
the behavior of the coefficients, a and b. Figure 2.5 shows
a and b as the functions of time based on Eq. (2.28). In
general, positive a, as shown in Fig. 2.5 (a), corresponds to the
positive energy dissipation, thus it has stabilizing effect. On the other
hand, b, the restoring term, is negative at small t for all
wave numbers shown in Fig. 2.5 (b), thus destabilizing the interface. As
the wave number increases, b becomes positive during spreading due
to the presence of surface tension, thus stabilizing the corresponding
perturbation.
However, there is no simple method but numerical simulation to
exactly predict the most dangerous wave number and the rate of growth for
the shape perturbation because of time dependent coefficients of Eq. (2.23).
Based on the base solutions, we numerically solve Eq. (2.23) under given
initial conditions such as 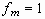 and
and 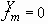 , and
, and 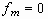 and
and 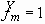 . The modified Euler
method has been employed to solve the initial value problem (Nakamura 1991).
. The modified Euler
method has been employed to solve the initial value problem (Nakamura 1991).
Factors which determine the magnitude of deceleration of a liquid
interface, i.e. the driving mechanism of the Rayleigh-Taylor instability,
include the initiation time of perturbation as well as the coefficient
A. Mathematical singularity occurs as 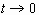 when both the velocity and the deceleration of the sheet reach infinity.
We physically reason that the sheet emerges from a finite initial radius
which corresponds to a finite nonzero initiation time. Since there is no
conclusive experimental data on exactly when the liquid sheet emerges,
we examine the sensitivity of the perturbation analysis to the perturbation
onset time
when both the velocity and the deceleration of the sheet reach infinity.
We physically reason that the sheet emerges from a finite initial radius
which corresponds to a finite nonzero initiation time. Since there is no
conclusive experimental data on exactly when the liquid sheet emerges,
we examine the sensitivity of the perturbation analysis to the perturbation
onset time 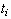 . On the other
hand, effects of impact inertia and surface tension are manifested through
Weber number in our analysis. Presence of surface tension that stabilizes
the interface leads to the mode of maximum instability. In the following
we present the numerical simulation results including the roles of such
parameters as described above.
. On the other
hand, effects of impact inertia and surface tension are manifested through
Weber number in our analysis. Presence of surface tension that stabilizes
the interface leads to the mode of maximum instability. In the following
we present the numerical simulation results including the roles of such
parameters as described above.
Figure 2.6 shows the temporal evolution of shape perturbations
for different wave numbers. For a computation time range, we used the limit
to which Eq. (2.27) holds, i.e. 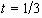 .
Perturbations of different wave numbers compete with one another and the
mode number of maximum instability varies with time, unlike time-independent
coefficient systems. In addition, neither the growth rate of the perturbation
nor the cutoff wave number is easily defined. As predicted in Fig. 2.5,
the perturbations of high wave numbers are stabilized as t increases
although the instants when the amplitudes alter their slopes do not exactly
coincide with those at which the b's change the sign.
.
Perturbations of different wave numbers compete with one another and the
mode number of maximum instability varies with time, unlike time-independent
coefficient systems. In addition, neither the growth rate of the perturbation
nor the cutoff wave number is easily defined. As predicted in Fig. 2.5,
the perturbations of high wave numbers are stabilized as t increases
although the instants when the amplitudes alter their slopes do not exactly
coincide with those at which the b's change the sign.
Figure 2.7 (a) shows that there exists a wave number which maximizes
the amplitude perturbation at every moment during spreading. Furthermore,
the number tends to decrease during spreading (Fig. 2.7 (b)). More studies
are required to understand how fingers merge during spreading and which
wave number manifests itself in the competition of many modes during spreading.
Such questions are expected to be anwered by considering nonlinear effects
of finite amplitude perturbations, which are beyond the scope of the present
work. However, it is clear that high wave numbers excited in earlier stages
are overwhelmed by lower wave numbers in the course of spreading as the
deceleration gradually comes to a stop. It is also noted that disturbances
of very high wave numbers are rapidly stabilized by surface tension.
Effects of the coefficient A, or the expansion rate of the
liquid sheet, on instability are shown in Fig. 2.8. We note that when the
sheet radius is given by Eq. (2.28), a high expansion rate due to large
A results in a high magnitude of deceleration, which eventually
promotes the instability of higher wave numbers. Figure 2.9 illustrates
the effect of perturbation onset time on instability. Perturbations initiated
earlier exhibit larger deceleration thus promoting instability of higher
wave number. However, it is noteworthy that the analysis results are rather
insensitive to 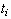 . Figure
2.10 presents the role of Weber number on the instability. As Weber number
increases, that is, when the effect of surface tension is weakened and
that of inertia strengthened, the higher wave numbers are more excited.
It is consistent with Thoroddsen and Sakakibara's (1998) observation that
higher impact speed results in greater finger numbers.
. Figure
2.10 presents the role of Weber number on the instability. As Weber number
increases, that is, when the effect of surface tension is weakened and
that of inertia strengthened, the higher wave numbers are more excited.
It is consistent with Thoroddsen and Sakakibara's (1998) observation that
higher impact speed results in greater finger numbers.
2.4. Conclusions
We developed a linear perturbation theory of interface instabilities
of a radially-expanding, liquid sheet in cylindrical geometries. The theory
was applied to an expanding sheet under a spreading droplet to elucidate
the origin of splashing. The base flow solutions were estimated by using
mass conservation. It was shown that significant deceleration occurs in
the early stages of spreading, which triggers the Rayleigh-Taylor instability.
The model supposes that the main factor inducing the deceleration is not
the viscosity but the continuity of flow around the impact region. The
theory was able to predict the most rapidly growing mode of azimuthal disturbance
and its growth rate at each instant during spreading. It was found that
the mode number of maximum instability changes because of time-dependent
coefficients in the amplitude equation. We examined effects of several
parameters on the analysis results including the transient profile of an
interface radius, i.e. the coefficient A, the perturbation onset
time, 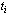 , and Weber number.
, and Weber number.
It is noted that the parameters examined above, A, 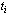 ,
and We, are interrelated with each other in reality: the impact inertia
and surface energy not only affect Weber number but they also determine
the collapsing dynamics of the droplet and sheet expansion characteristics:
A and
,
and We, are interrelated with each other in reality: the impact inertia
and surface energy not only affect Weber number but they also determine
the collapsing dynamics of the droplet and sheet expansion characteristics:
A and 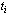 . In addition,
it is known that substrate roughness plays a significant role in splashing
(Stow and Hadfield 1981). The roughness may affect the values of A
and
. In addition,
it is known that substrate roughness plays a significant role in splashing
(Stow and Hadfield 1981). The roughness may affect the values of A
and 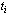 and change the mode
of the maximum instability as well as destabilize the perturbation of a
given wave number. On the other hand, the effects of thermal conditions
of the target surface are to be considered especially when a droplet hits
a surface as hot as its boiling temperature (Chandra and Avedisian 1991)
or when a molten droplet impinges on a subcooled target (Pasandideh-Fard
1998). Understanding of these topics calls for more studies in the future.
and change the mode
of the maximum instability as well as destabilize the perturbation of a
given wave number. On the other hand, the effects of thermal conditions
of the target surface are to be considered especially when a droplet hits
a surface as hot as its boiling temperature (Chandra and Avedisian 1991)
or when a molten droplet impinges on a subcooled target (Pasandideh-Fard
1998). Understanding of these topics calls for more studies in the future.
In conclusion, we find that the rapidly expanding liquid sheet
released upon droplet collision with a solid target is subjected to Rayleigh-Taylor
instability. Numerical computations of the transient evolution of shape
perturbations are able to determine the most rapidly growing wave number
and the growth rate of perturbation amplitudes. Our analysis reveals that
larger impact inertia associated with higher We, and thus presumably higher
A, promotes interface instability and prefers higher wave number
for maximum instability. However, further analysis is required to accurately
determine the correlation between the sheet expansion profile and impact
conditions. We relate this instability with the fundamental mechanism of
splashing from the viewpoint that the inherent feature of splashing is
an unstable expansion of the spreading front of droplets.
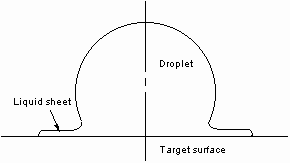
FIGURE 2.1. Release of a liquid sheet upon the droplet collision
with a solid target.
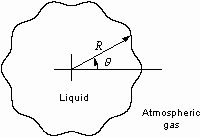
FIGURE 2.2. Disturbed liquid sheet which expands radially.
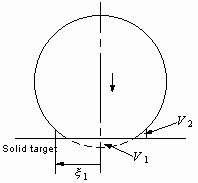
(a)
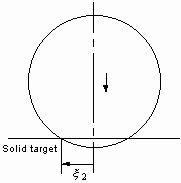
(b)
FIGURE 2.3. Limiting cases of droplet spreading.
The original droplet radius and velocity are both unity after nondimensionalization.
(a) Volume 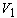 is displaced
to
is displaced
to 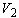 while the droplet descends
with the speed of unity. The cylinder radius
while the droplet descends
with the speed of unity. The cylinder radius 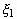 is expressed as Eq. (23). (b)
is expressed as Eq. (23). (b) 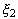 is the intersection radius of the target surface and the droplet traveling
with no deformation.;
is the intersection radius of the target surface and the droplet traveling
with no deformation.;
FIGURE 2.4. (a) Transient radius profiles of an expanding
liquid sheet expressed as 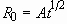 .
(b) Corresponding deceleration. Note that the significant deceleration
is experienced by the interface immediately after impact, which drives
the Rayleigh-Taylor instability.;
.
(b) Corresponding deceleration. Note that the significant deceleration
is experienced by the interface immediately after impact, which drives
the Rayleigh-Taylor instability.;
FIGURE 2.5. The coefficients of Eq. (23) when 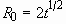 and
and 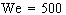 . (a) The coefficient
a is given by
. (a) The coefficient
a is given by 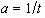 .
(b) The coefficient b vs. time for various wave numbers.;
.
(b) The coefficient b vs. time for various wave numbers.;
FIGURE 2.6. (a) Temporal evolution of the shape amplitudes
of various wave numbers until 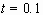 .
(b) Temporal evolution of the shape amplitudes until
.
(b) Temporal evolution of the shape amplitudes until 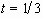 .
Initial conditions at
.
Initial conditions at 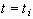 are
are 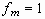 and
and 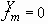 .
The computation was performed for
.
The computation was performed for 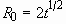 ,
, 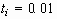 ,
and
,
and 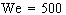 . Perturbations of
. Perturbations of 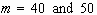 are exceeded by that of
are exceeded by that of 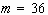 during spreading. Perturbations of
during spreading. Perturbations of  decay after initially growing period. The perturbation amplitude of
decay after initially growing period. The perturbation amplitude of 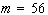 even decays to the value less than the initially assigned one before t
reaches
even decays to the value less than the initially assigned one before t
reaches 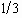 . We define a wave
number, which is less than the so-found wave number by one, as a pseudo-cutoff
wave number - in this case, it is 55.;
. We define a wave
number, which is less than the so-found wave number by one, as a pseudo-cutoff
wave number - in this case, it is 55.;
FIGURE 2.7. (a) Perturbation amplitude vs. wave numbers
for different time. Initial conditions for solid lines are 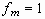 and
and 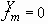 . Initial conditions
for a dotted line are
. Initial conditions
for a dotted line are 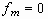 and
and 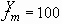 . The computation was
performed for
. The computation was
performed for 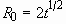 ,
, 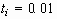 ,
and
,
and 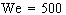 . (b) Changes of a
mode number of maximum instability and a pseudo-cutoff wave number with
time. Computation conditions are those of the solid lines in (a). (c) Growth
of azimuthal disturbances during spreading at the modes of maximum instability.
From the innermost corrugated circle,
. (b) Changes of a
mode number of maximum instability and a pseudo-cutoff wave number with
time. Computation conditions are those of the solid lines in (a). (c) Growth
of azimuthal disturbances during spreading at the modes of maximum instability.
From the innermost corrugated circle, 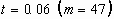 ,
, 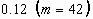 ,
, 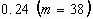 ,
and
,
and 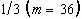 . Initial conditions
are
. Initial conditions
are 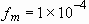 and
and 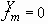 .
The other conditions are identical to those of (a).;
.
The other conditions are identical to those of (a).;
FIGURE 2.8. Effect of the coefficient A on
instability. (a) Wave number of maximum instability vs. A. (b) Perturbation
amplitude of those numbers vs. A.
FIGURE 2.9. Effect of the perturbation onset time 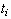 on instability. (a) Wave number of maximum instability vs.
on instability. (a) Wave number of maximum instability vs. 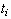 .
(b) Perturbation amplitude of those numbers vs.
.
(b) Perturbation amplitude of those numbers vs. 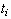 .;
.;
FIGURE 2.10. Effect of Weber number on instability.
(a) Wave number of maximum instability vs. We. (b) Perturbation amplitude
of those numbers vs. We.
CHAPTER 3
THE OSCILLATIONS OF LIQUID DROPLETS UPON
COLLIDING WITH SOLID SURFACES
3.1. Introduction
This chapter aims to investigate the oscillations of liquid droplets
upon colliding with solid surfaces which depend on various dynamic and
wetting conditions. The post-impact oscillations of a liquid droplet consist
of the initial spreading of the droplet until it reaches its maximum base
diameter and subsequent oscillatory motions of recoiling and re-spreading,
if any. Dynamics of liquid droplets colliding with solid surfaces has been
extensively studied for more than a century (Worthington 1877a,b). However,
the majority of this effort has been focused on the initial spreading process,
i.e. from the moment of impact to the moment when the droplet reaches its
maximum base diameter (Engel 1955; Harlow and Shannon 1967; Stow and Hadfield
1981; Tsurutani et al. 1990; Trapaga and Szekely 1991; Shi and Dear 1992).
As a result, it appears to be only recent that the post-impact oscillations
gained the full interests of the scientific communities.
Fukai et al. (1995) conducted a theoretical study on the spreading
and recoiling of a liquid droplet upon colliding with a solid surface.
In the study, the numerical simulation results were compared with experimental
data that used water droplets and Pyrex glasses of different surface roughness
and a wax coating as the target materials. To account for the effects of
wetting, different values for the advancing and receding contact angles,
measured while allowing droplets to slide down an inclined test surface,
were adopted per target material. Their model is based on solving the full
Navier-Stokes equation by utilizing deforming finite elements and allowing
the contact line to slip. Their prediction was generally in good agreement
with experimental measurements. Pasandideh-Fard et al. (1996) performed
a similar study by numerically solving the full Navier-Stokes equation
using a modified SOLA-VOF method and a no-slip boundary condition. In the
experiments, droplets of water with different surfactant concentrations
were deposited on polished, stainless steel surfaces. Dynamic contact angles
were measured from photographs and the values were used as a boundary condition
for the numerical model. Their model accurately predicted experimental
measurements taken during the spreading stages. However, a discrepancy
was found during the recoiling stages. Zhang and Basaran (1997) performed
an experimental study using distilled water and aqueous surfactant solutions
as the droplet material and glass as the target surface. They measured
the long-time behavior, i.e. oscillation, of a liquid droplet using high
speed video. They found that the decrease of surface tension due to the
presence of a surfactant enhanced the spreading while Marangoni stresses
induced by non-uniform surfactant distribution inhibited the spreading.
Studies of the oscillation dynamics of sessile and pendant drops
began only recently. An extensive review on the subject is given by Wilkes
and Basaran (1997) and will not be repeated in this chapter. Since the
studies concern the motion of supported droplets, i.e. drops placed on
solid supports a priori., the effect of impingement with the solids
on the droplet dynamics is beyond the scope of the studies. Schiaffino
and Sonin (1997) discussed the oscillations of a droplet's centerline elevation
after its footprint is arrested by freezing on a subcooled target of its
own kind. They found that the oscillation damping time of deposited water
droplets is in good agreement with the damping time of a negligibly viscous,
liquid drop which oscillates freely.
Our theoretical study is motivated by a unique approach, originated
by Kendall and Rohsenow (1978) and Bechtel et al. (1981), to the dynamics
of the droplet impact. The approach is based on the variational principle
rather than on the Navier-Stokes equation which requires significant computational
efforts. Its advantage is that by assuming the geometry of the deforming
droplet, a very simple differential equation is obtained to describe the
droplet dynamics. From the experimental aspect, the current study aims
to investigate the spreading and subsequent oscillations of various liquid
droplets upon colliding with different solid surfaces. Although similar
experimental studies have been performed by previously mentioned authors
(Fukai et al.; Pasandideh-Fard et al.; and Zhang and Basaran), this study
not only examines a broad spectrum of dynamic impact conditions such as
Weber number and Reynolds number, but also investigates the wetting effects
caused by various combinations of liquid droplets and solid targets. In
this chapter, we compare the modeling results and the experimental measurements
to show the capability of our model to predict the complicated phenomena
of the droplet spreading.
3.2. Modeling
We model the oscillations of a droplet by adopting the variational
principle instead of solving the Navier-Stokes equation with moving boundaries.
We assume two different droplet shapes in performing the variational method,
i.e., a cylinder and a truncated sphere. We derive the cylinder model in
a similar manner to Kendall and Rosehnow's model (1978). Our model extends
theirs to include the wetting properties of the liquid droplet with a solid
surface and the frictional dissipation. In addition, the initial conditions
are determined to satisfy the energy conservation exactly. A variational
method using a truncated sphere was derived by Bechtel et al. (1981), and
we briefly introduce their results as well.
3.2.1. Formulation of the problem using a cylinder model
The variational principle can be written as (Crandall et al. 1968):
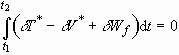 , (3.1)
, (3.1)
where 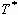 denotes
the kinetic coenergy,
denotes
the kinetic coenergy, 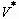 the potential energy, and t the time. The frictional work
the potential energy, and t the time. The frictional work 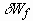 is expressed as
is expressed as
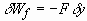 (3.2)
(3.2)
where F denotes the frictional force and y the displacement
of the frictional motion. In a case where the frictional force is due to
the wall shear stress, we write Eq. (3.1) as
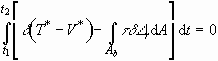 , (3.3)
, (3.3)
where 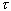 is the shear
stress at the base of the droplet,
is the shear
stress at the base of the droplet, 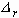 the radial displacement, and
the radial displacement, and 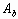 the base area. Each term in the integrand can be evaluated when the shape
of the deforming droplet and the velocity profile are known. The initial
velocity and the diameter of the original droplet before collision are
the base area. Each term in the integrand can be evaluated when the shape
of the deforming droplet and the velocity profile are known. The initial
velocity and the diameter of the original droplet before collision are 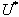 and
and 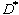 , respectively. The
droplet has the density
, respectively. The
droplet has the density 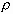 ,
the surface tension
,
the surface tension 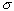 , and
the viscosity
, and
the viscosity 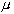 . We choose
. We choose 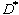 ,
, 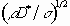 ,
and
,
and 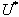 as the characteristic
length, time and velocity scales, respectively. The following quantities
are nondimensionalized based on those scales unless noted otherwise, and
their forms are summarized in Appendix C.
as the characteristic
length, time and velocity scales, respectively. The following quantities
are nondimensionalized based on those scales unless noted otherwise, and
their forms are summarized in Appendix C.
We model the oscillating droplet on a solid surface as a cylinder
whose base diameter and height are 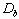 and h, respectively, as shown in Fig. 3.1. The volume of the cylinder
is the same as that of the droplet, thus
and h, respectively, as shown in Fig. 3.1. The volume of the cylinder
is the same as that of the droplet, thus
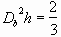 (3.4)
(3.4)
is satisfied for any 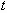 .
If either
.
If either 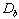 or
or 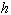 is specified in time, the other is known straightforwardly by Eq. (3.4).
Therefore, it is enough to simulate the temporal evolution of either
is specified in time, the other is known straightforwardly by Eq. (3.4).
Therefore, it is enough to simulate the temporal evolution of either 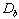 or
or 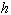 to fully describe the
dynamics of the oscillating cylinder. We derive the equation for
to fully describe the
dynamics of the oscillating cylinder. We derive the equation for 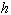 in the following.
in the following.
Assuming axisymmetric motion, the nondimensional kinetic coenergy
is written as
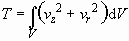 , (3.5)
, (3.5)
where 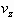 and
and 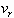 denote the axial and radial velocity of the flow inside the cylinder, respectively.
For the energy and volume scales, we choose
denote the axial and radial velocity of the flow inside the cylinder, respectively.
For the energy and volume scales, we choose 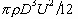 ,
and
,
and 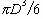 , which correspond
to the original kinetic coenergy and the volume of the colliding droplet,
respectively. We relate the axial velocity
, which correspond
to the original kinetic coenergy and the volume of the colliding droplet,
respectively. We relate the axial velocity 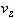 with h as
with h as
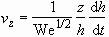 , (3.6)
, (3.6)
where We is the Weber number defined as 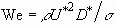 .
The radial velocity
.
The radial velocity 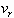 is
given by continuity as
is
given by continuity as
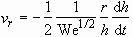 . (3.7)
. (3.7)
The flow field given by Eq. (3.6) and (3.7) is that of the potential
flow which satisfies the Laplace equation. Substituting Eqs. (3.6) and
(3.7) into Eq. (3.5) and performing integration over the volume of the
cylinder, we obtain
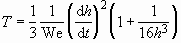 . (3.8)
. (3.8)
In evaluating the potential energy we do not include gravity since
we are mainly interested in the oscillation due to interfacial phenomenon.
Hence the potential energy V is written as
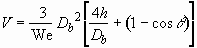 , (3.9)
, (3.9)
where 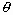 is the equilibrium
contact angle between the liquid droplet and the solid surface. By using
Eq. (3.4), we express the potential energy by
is the equilibrium
contact angle between the liquid droplet and the solid surface. By using
Eq. (3.4), we express the potential energy by 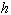 only:
only:
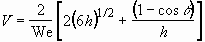 . (3.10)
. (3.10)
The dissipative work is estimated in the same manner as Bechtel
et al.'s (1981). Since the potential flow field we obtained does not afford
the viscous effects, we estimate the external viscous stress, 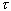 ,
based on that of the oscillating stagnation flow with the period
,
based on that of the oscillating stagnation flow with the period 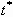 .
Defining the characteristic hydrodynamic boundary layer thickness
.
Defining the characteristic hydrodynamic boundary layer thickness 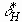 as
as
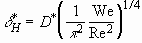 , (3.11)
, (3.11)
we write
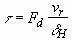 , (3.12)
, (3.12)
where 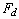 is the dissipation
factor. We choose
is the dissipation
factor. We choose 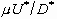 as the
characteristic stress scale
as the
characteristic stress scale 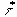 .
Substitution of Eq. (3.7) into Eq. (3.12) yields
.
Substitution of Eq. (3.7) into Eq. (3.12) yields
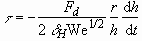 . (3.13)
. (3.13)
The radial displacement 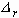 is written, in the present nondimensionalization, as:
is written, in the present nondimensionalization, as:
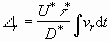 . (3.14)
. (3.14)
Substituting Eq.(3.7) into Eq. (delta r) we obtain
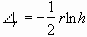 , (3.15)
, (3.15)
where we arbitrarily set the integration constant to zero since 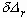 is of our interest.
is of our interest.
Performing the variation of the kinetic coenergy with respect to 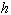 and using integration by parts, we get
and using integration by parts, we get
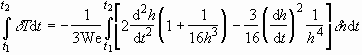 . (3.16)
. (3.16)
By a similar procedure, we obtain
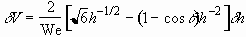 , (3.17)
, (3.17)
and
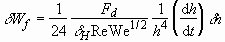 . (3.18)
. (3.18)
On substituting Eqs. (3.16), (3.17), and (3.18) into Eq. (3.3),
we require that the coefficient of 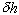 should be zero for the variational formula to be satisfied. After arrangement,
we obtain an equation to describe the temporal evolution of h:
should be zero for the variational formula to be satisfied. After arrangement,
we obtain an equation to describe the temporal evolution of h:
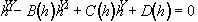 , (3.19)
, (3.19)
where the dot denotes 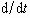 .
The coefficients are give by
.
The coefficients are give by
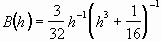 , (3.20)
, (3.20)
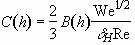 , (3.21)
, (3.21)
and
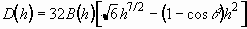 . (3.22)
. (3.22)
The initial conditions, i.e., 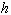 and
and 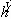 at
at 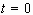 ,
should be specified to solve Eq. (3.19). Since the original droplet and
a cylinder have a substantial difference in shape, we seek initial conditions
which ensure that the initial kinetic coenergy and potential energy of
the cylinder are the same as those of the original droplet. In addition,
the volume must be conserved as stated in Eq. (3.4). The equality of initial
potential energies of the original droplet and a cylinder yields the following
relation:
,
should be specified to solve Eq. (3.19). Since the original droplet and
a cylinder have a substantial difference in shape, we seek initial conditions
which ensure that the initial kinetic coenergy and potential energy of
the cylinder are the same as those of the original droplet. In addition,
the volume must be conserved as stated in Eq. (3.4). The equality of initial
potential energies of the original droplet and a cylinder yields the following
relation:
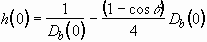 . (3.23)
. (3.23)
Further arrangement of Eq. (3.23) is made by using Eq. (3.4):
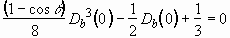 . (3.24)
. (3.24)
Therefore, Eqs. (3.24) and (3.4) determine the initial diameter
and height of the cylinder. The initial 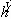 is given by the equality of the kinetic coenergies:
is given by the equality of the kinetic coenergies:
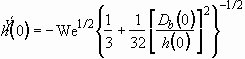 (3.25)
(3.25)
We note that the initial diameter and height of the cylinder depends
solely on the contact angle 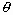 ,
and Fig. 3.2 shows
,
and Fig. 3.2 shows 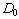 and
and 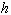 versus
versus 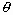 .
.
Summarizing our problem formulation, the second order nonlinear
differential equation, Eq. (3.19), completely describes the dynamics of
a liquid cylinder oscillating on a solid surface. The initial value problem
can be solved numerically with the initial conditions specified by Eqs.
(3.23), (3.24), and (3.25).
3.2.2. Formulation of the problem using a truncated sphere model
We briefly present Bechtel et al.'s truncated sphere model in this
section with the estimation of the frictional term modified. The geometry
of a truncated sphere is shown in Fig. 3.3. They assumed the same velocity
profiles as we did in the cylinder model above, and the equation for the
temporal evolution of h is given by
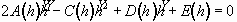 , (3.26)
, (3.26)
where the coefficients are given by
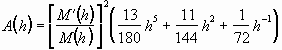 , (3.27)
, (3.27)
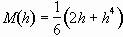 , (3.28)
, (3.28)
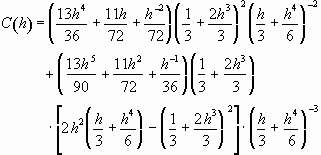 (3.29)
(3.29)
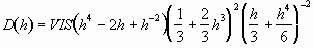 , (3.30)
, (3.30)
and
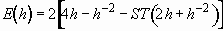 . (3.31)
. (3.31)
The parameters ST and VIS are given, in the present
nondimensionalization, by
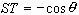 (3.32)
(3.32)
and
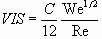 (3.33)
(3.33)
where C is related to the boundary layer thickness of an
oscillating flow with the period 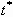 and Re denotes the Reynolds number defined as
and Re denotes the Reynolds number defined as 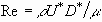 ;
; 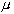 being the viscosity. We modify Bechtel et al.'s model to include the dissipation
factor,
being the viscosity. We modify Bechtel et al.'s model to include the dissipation
factor, 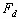 , in the estimation.
Thus, C is given by
, in the estimation.
Thus, C is given by
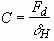 , (3.34)
, (3.34)
where 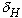 is given
by Eq. (3.11). The base diameter is related to h by
is given
by Eq. (3.11). The base diameter is related to h by
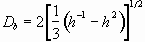 . (3.35)
. (3.35)
Since the initial droplet shape assumed by this model accurately
represents the real spherical shape, the initial conditions are obtained
straightforwardly. The initial height is set equal to the original diameter
of the droplet and the initial velocity is set equal to the velocity of
the droplet prior to collision. After nondimensionalization, we write
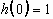 , (3.36)
, (3.36)
and
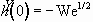 . (3.37)
. (3.37)
However, we note that while the exact value of the initial kinetic
coenergy is 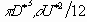 , its value
given by this model is
, its value
given by this model is 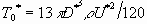 due to the assumed velocity profile.
due to the assumed velocity profile.
3.3. Description of the experimental apparatus
The experimental apparatus is illustrated in Fig. 3.4. It consists
of a pipette which gently ejects a liquid droplet, a flat target on which
the droplet falls, a high-speed video system, and a stroboscope which is
synchronized with the video system. As the experimental liquids, deionized
water, ink, and silicone oil (Dow Corning 704 diffusion pump oil) are used.
Table "3-properties" shows the physical properties of the liquids. To examine
various collision conditions, the velocity prior to impact is varied by
changing the distance between the pipette and the target. In addition,
two different sizes of pipettes are used to vary the original droplet diameter.
Acrylic and silicone oxide (SiO2) are used as the
target surfaces. The equilibrium contact angles between the liquids and
the surfaces are measured to evaluate the wetting characteristics The measurement
procedure and the values are presented in Appendix D.
The spreading and subsequent oscillation of a droplet on a solid
surface is recorded with a high speed video system (Kodak Ektapro EM, Model
1012) at a rate of 1000 frames per second. An image stored in the system
consists of 192 X 239 pixels. The illumination is provided by a stroboscope,
which is synchronized with the camera; thus, very sharp images can be captured.
The stored images in the digital memory are downloaded onto a video tape
using a S-VHS video tape recorder, and analyzed by an image analysis software
which is capable of measuring the dimensions of objects by the number of
pixels. An object of a known size (8 mm in diameter) is recorded by the
same video setup and used for calibration. In addition, to obtain the highly
accurate conditions of the droplet impact, the weight of the droplet is
measured during each experiment. The diameter deduced by the weight-measurement
method is compared with that obtained by the image calibration. The values
are in very close agreement in all cases, with less than 2% discrepancy.
Using the image analysis software, we measure the base diameter of the
droplet at each frame to determine the temporal evolution of droplet oscillations.
3.4. Experimental and modeling results
In this section, we present experimental observations on the oscillations
of different liquid droplets on different target surfaces. In addition,
we compare our measurement results with the predictions of the models discussed
above. Figure 3.5 shows the dynamics of a water droplet colliding with
an acrylic surface. Two very different kinds of dynamic impact behavior
are shown in the figure. The oscillating droplet of Fig 3.5 (b) exhibits
a much smaller base diameter and thus, higher centerline elevation than
that of (a). The droplet motion after the first oscillation period, i.e.,
after the first recoiling is completed, is much more vigorous in (b) than
(a), as well. It is well known that high impact inertia associated with
high Weber number and Reynolds number results in a greater spread factor 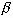 .
The spread factor is defined as the ratio of the maximum base diameter
during spreading to the original droplet diameter:
.
The spread factor is defined as the ratio of the maximum base diameter
during spreading to the original droplet diameter: 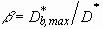 .
High Weber number also induces an unstable spreading front as observed
by other researchers (Allen 1975, Thoroddsen and Sakakibara 1998). In addition,
our figure shows that high impact inertia, i.e., high We and Re, results
in vigorous post-impact oscillations relative to those generated by low
inertia impact.
.
High Weber number also induces an unstable spreading front as observed
by other researchers (Allen 1975, Thoroddsen and Sakakibara 1998). In addition,
our figure shows that high impact inertia, i.e., high We and Re, results
in vigorous post-impact oscillations relative to those generated by low
inertia impact.
The temporal evolution of the base diameter of the oscillating
droplet was measured and the results are shown in Fig.3.6. The vigorous
oscillations of the droplet with high impact inertia are clearly observed
as well as the increased spread factor in the initial stages of the spreading.
Next, we compare the predictions of the models with the experimental data,
in Fig. 3.7. We present the results of three different models, the cylinder
model with two different, initial base diameters and the truncated sphere
model. Dissipation factors are empirically determined to best fit the experimental
data in general. In the low impact inertia case as shown in Fig. 3.7 (a),
both the cylinder model with the smaller initial base diameter and the
truncated sphere model show qualitatively good agreement with the experimental
measurements. Figure 3.7 (b) shows that the cylinder models with two different
initial diameters yield almost identical results and that they closely
predict the experimental measurements. However, the truncated sphere model
deviates significantly from the experimental data. Figure 3.7 (c), the
high impact inertia case, shows that the cylinder model with the greater
initial base diameter predicts the experimental results very well.
In general, we observe that the cylinder model better predicts
the experiments than the truncated sphere model. This is easily explained
by investigating the images in Fig 3.5. The recoiling droplet resembles
a cylinder more closely than the truncated sphere. Nevertheless, we note
that the truncated sphere model succeeds in predicting the initial spreading
stage before the droplet reaches the maximum base diameter in all the cases.
This is because the truncated sphere represents the shape of the collapsing
droplet in the inital stages with sufficient accuracy.
Next, we examine the effect of the target solids on the droplet
dynamics. Figures 3.8 (a) and (b) compare the base diameters of water and
ink droplets, respectively, on different target surfaces, acrylic and silicon
oxide. We note that water and ink commonly wet the silicon oxide surface
better than the acrylic surface. Under similar impact conditions, the base
diameters in the initial spreading stage are essentially alike. However,
in the recoiling stage, the droplet deposited onto the acrylic (poor wetting
surface) retracts its base diameter faster than the droplet on the silicon
oxide (nice wetting surface). We use the cylinder model to simulate the
dynamics of the water droplets and the truncated sphere model for the ink
droplets. The images in Fig. 3.9 confirm the validity of using the truncated
sphere model, instead of the cylinder model, for ink droplets. The agreeement
between the predictions and the experimental data is very strong in each
case.
Figure 3.10 illustrates the dynamic behavior exhibited by droplets
of different liquids colliding with the same target surface. Although the
Weber numbers of the impacting droplets are similar, the variation in the
liquid properties causes a significant difference in the Reynolds number
and the contact angle. We observe that the decrease in the Reynolds number
reduces the spread factor in both Fig. 3.10 (a) and (b). Furthermore, the
recoiling is less pronounced when wetting is improved (see the equilibrium
contact angles in Appendix D). In all the cases, the models predict the
experimental results very closely. Images of a silicone oil droplet colliding
with an acrylic surface are shown in Fig. 3.11. After the silicone oil
droplet recoils to form a relatively tall truncated sphere, it spreads
to a very thin film since its equlibrium contact angle with the acrylic
is very small.
Having investigated the effets of impact conditions on the post-impact
oscillations, we examine the individual effect of impact conditions such
as the Weber number, the Reynolds number, and the contact angle on the
droplet dynamics, through theoretical modeling. Figures 3.12 (a) and (b)
show the effects of the Weber number and the Reynolds number, respectively,
on the temporal evolution of the base diameter. For these graphs, the contact
angle between a water droplet and acrylic surface is used. We use the cylinder
model which has been proven to best fit the experimental data for water
droplets on acrylic, as shown above. Although a higher Weber number and
a higher Reynolds number both increase the spread factor, the recoiling
processes show different features. With the same Reynolds number, droplets
with low Weber number recoil faster and require less time to return to
the equibrium base diameter. On the other hand, when the Weber number remains
constant, droplets with higher Reynolds number recoil faster than those
with low Reynolds number. Figure 3.12 (a) can be explained as follows.
Low Weber number implies that the relative magnitude of the surface energy
to the initial impact energy is greater than high Weber number, and thus,
this contributes to the faster recoiling which is a surface-energy dominated
phenomenon. Furthermore, the increase in the degree of spreading due to
the high Weber number, causes more viscous dissipation even at the same
Reynolds number. This is because as the base area increases, more friction
is experienced by the droplet on the target surface. On the other hand,
the events depicted in Figure 3.12 (b) are explained as follows. Droplets
with high Reynolds number experience less viscous dissipation. Therefore,
droplets with higher Reynolds number recoil faster when the relative magnitude
of the surface energy to the initial impact energy is the same.
The effect of contact angle on droplet oscillations is illustrated
in Fig. 3.12 (c). We show the temporal evolution of the base diameter dependent
upon the contact angle while keeping the Weber number and Reynolds number
constant. As the contact angle decreases, the spread factor increases owing
to the improved wetting. The recoiling process is fairly sensitive to the
contact angle such that the droplets with higher contact angle (poor wetting)
retract much faster than those with lower contact angle.
3.5. Discussions and conclusions
We have investigated the spreading and subsequent oscillations
of various liquid droplets upon colliding with different solid surfaces.
In our experiments, sequential images of the impacting droplets are captured
by a high speed video system. We analyze the images to obtain the temporal
evolution of the base diameter of the droplet. To understand the physical
phenomena, we develop a model based on the variational principle, assuming
the droplet shape to be cylindrical. We also modify an existing variational
model which assumes the droplet to be a truncated sphere.
Our experiments show that droplets with high impact inertia, associated
with high We and Re, oscillate more vigorously upon colliding with the
solid surface. The oscillation is greatly affected by the wetting between
the liquid droplet and the solid surface. Nice wetting weakens and slows
down the recoiling process. Moreover, experiments using droplets of different
liquids and the same target solid show the strong effects of liquid properties
and wetting behavior on the oscillation phenomena. Modeling results are
in good agreement with the experimental data, demonstrating the capability
of our models to predict the complicated phenomena of the droplet spreading
and recoiling. In addtion, the individual effects of parameters such as
We, Re, and the contact angle are examined by using our model. The analysis
shows that surface energy and viscous dissipation play critical roles in
determining droplet dynamics. It is also shown through the model that the
droplet dynamics are strongly affected by the contact angle, thus, poor
wetting greatly promotes the recoiling.
When the recoiling of the liquid droplet is vigorous, we may even
observe a necking of the liquid column moving upward, as shown in Fig.
3.13. Similar phenomena were observed by Wachters and Westerling (1966)
and Chandra and Avedisian (1991). Their observations were made on liquid
drops impacting heated targets above the boiling temperature of the liquid.
It is interesting to note that Chandra and Avedisian observed a very different
recoiling process for different target temperatures. According to their
measurement, the contact angle strongly depends on the target temperature.
Therefore, the droplets hitting hot surfaces with a large contact angle
recoil very vigorously while the droplets do not exhibit such recoiling
on cold surfaces with small contact angle. This is consistent with our
experimental observations.
In both the cylinder and the truncated sphere models, it is necessary
to determine the dissipation factor, 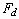 .
We have determined the values such that the modeling results best fit the
experimental data. Although the method is purely empirical, we find that
the values are constant for each liquid and for each model regardless of
the target material. The values of
.
We have determined the values such that the modeling results best fit the
experimental data. Although the method is purely empirical, we find that
the values are constant for each liquid and for each model regardless of
the target material. The values of 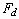 used in our simulation are summarized in Table 3.2.
used in our simulation are summarized in Table 3.2.
Our models using the variational principle predict the experimental
data surprisingly well, considering their approximate nature. A significant
computational effort is saved by solving a single second-order, nonlinear
differential equation instead of solving the full Navier-Stokes equation
with the moving boundary. Furthermore, our current study shows that by
using the equilibrium contact angle, the experimental measurements can
be predicted very closely. However, we see room where the dynamic contact
angles may improve the prediction accuracy especially for water droplets
on acrylic. The measurements show that the base diameter remains for a
finite time around the maximum spread diameter while our cylinder model
predicts an immediate recoiling. In reality, the droplet spends more time
than the model predicts before the recoiling starts due to the contact
angle hysterisis. While the droplet reverses its direction of motion, the
dynamic contact angle should change from the advancing angle to the receding
angle. That is, the recoilng is delayed in reality since the contact line
may stay at rest within a range of contact angles (contact angle hysterisis).
TABLE 3.1. Physical properties of the liquids used in the experiments
|
Liquid
|
Density (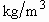 ) )
|
Surface tension (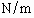 ) )
|
Viscosity (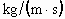 ) )
|
|
Water
|
996
|
0.0717
|
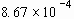
|
|
Ink
|
1052
|
0.055
|
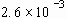
|
|
Silicone oil
|
1064
|
0.0373
|
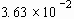
|
TABLE 3.2. Dissipation factors
|
Liquid
|
Assumed shape in model
|
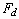
|
|
Water
|
Cylinder
|
15
|
|
Water
|
Truncated sphere
|
5.3
|
|
Ink
|
Truncated sphere
|
3.2
|
|
Silicone oil
|
Truncated sphere
|
3.2
|
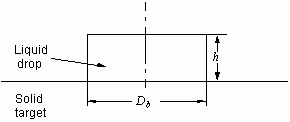
.1. Geometry of the cylinder model;
FIGURE 3.1. Geometry of the cylinder model
FIGURE 3.2. Initial diameter and height of the
cylinder versus contact angle as given by Eq. (3.24) and (3.4)
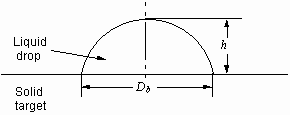
.3. Geometry of the truncated sphere model;
FIGURE 3.3. Geometry of the truncated sphere model
.4. Experimental apparatus for the high speed imaging
of the droplet oscillations;
FIGURE 3.4. Experimental apparatus for the high
speed imaging of the droplet oscillations
FIGURE 3.5. Images of a water droplet colliding with
acrylic surface. (a) Original droplet diameter = 3.6 mm, Impact velocity
= 0.77 m/s, We=30, Re=3214. (b) Original droplet diameter = 3.5 mm, Impact
velocity = 3.47 m/s, We=582, Re=13850.
FIGURE 3.6. The temporal evolution of the base diameter
of water droplets colliding with acrylic surface. The impact conditions
for triangles and squares are the same as the FIG. 3.5 (a) and (b), respectively.
The impact conditions for circles: Original droplet diameter = 3.7 mm,
Impact velocity = 1.63 m/s, We=137, Re=6950.
FIGURE 3.7. Predictions of the models and the experimental
measurements for water droplets on acrylic surface. Modeling results using
the truncated sphere model and the cylinder model are presented. In the
cylinder model, two different initial base diameters can be used as shown
in Fig. 3."D0 and h0 vs. theta", and both the results are shown.
FIGURE 3.8. Effect of target surfaces on droplet
dynamics. (a) Water droplet on acrylic and silicon oxide. (b) Ink droplet
on acrylic and silicon oxide.
FIGURE 3.9. Images of a ink droplet colliding with
acrylic surface. Original droplet diameter = 3.2 mm, Impact velocity =
1.75 m/s, We=190, Re=2296.
FIGURE 3.10. (a) Dynamic behavior of water, ink,
and silicone oil droplets colliding with the acrylic surface. (b) Dynamic
behavior of water, and ink droplets colliding with the silicon oxide surface.
FIGURE 3.11. Images of a silicone oil droplet colliding
with acrylic surface. Original droplet diameter = 2.8 mm, Impact velocity
= 1.44 m/s, We=166, Re=118.
FIGURE 3.12. (a) Effect of the Weber number. (b)
Effect of the Reynolds number. (c) Effect of the contact angle.
FIGURE 3.13. Necking of a rising water column during
a recoiling process.
CHAPTER 4
BOUNCING OF MOLTEN METAL DROPLETS UPON COLLIDING
WITH SOLID SURFACES
4.1. Introduction
The deposition of molten metal droplets is fundamental to many
industrial technologies, such as spray forming, thermal spraying, rapid
prototyping, and electronic packaging. Due to its practical applications,
the spreading behavior of molten droplets has been the subject of intense
study recently. Those studies mainly focus on the mechanism which arrests
the motion of a droplet spreading on a subcooled target. However, our current
study aims to investigate a rather strange behavior of molten metal droplets.
Under certain conditions, metal droplets do not stick to target surfaces
but rather, they bounce off. Spreading and the subsequent arrest by solidification
of molten droplets can occur only when bouncing is absent or prevented.
Understanding of bouncing phenomenon is especially important in electronic
packaging where an individual solder droplet is deposited and its shape
is critical for the quality of the connection (Waldvogel and Poulikakos
1997). In addition, since bouncing induces poor physical contact between
the droplet and its target, the quality of spray-formed deposits is greatly
affected by the phenomenon as well (Matson et al. 1998).
In this chapter, we examine the basic physics of the bouncing of
molten metal droplets. We investigate the effects of both the dynamic and
thermal conditions of the droplet impact on the bouncing. It is observed,
by high speed imaging, that bouncing is a very violent form of droplet
oscillation upon its collision with a solid surface. It is also observed
that the bouncing is prevented when the base of the droplet freezes faster
than recoiling can take place. Based on the observations, we develop a
simple model leading to a regime map which divides the bouncing and sticking
regions based on thermal and dynamic conditions.
4.2. Description of the experimental apparatus
Pure tin is used as the droplet material. We employ two different
methods to investigate the bouncing of molten tin droplets. The first method
is illustrated in Fig. 4.1. Tin is melted in a stainless steel crucible.
A thermocouple which is inserted in the crucible and a band heater which
is wrapped around the crucible are connected to a controller to maintain
a constant temperature of the melt. Molten material is ejected through
an orifice, 100 µm in diameter, by supplying high pressure, nitrogen
gas into the crucible. We observe that when initiating the ejection of
molten material, a certain pressure difference needs to be established
and that a jet is always formed instead of drops. After establishing a
jet, we rapidly relieve the pressure inside the crucible to produce molten
material in the form of a droplet. The diameter range of the droplets which
can be generated by such means, is from approximately 1.3 mm to 2.7 mm.
The molten droplet falls onto a solid target surface located 0.43 m below
the orifice. As the target solids, pure copper, 6061 aluminum alloy, pure
tin, silicon bronze, 304 stainless steel, and plane glass are used. All
the surfaces are polished with a 1-µm diamond paste except the glass
surface. The surface is heated underneath by an aluminum block in which
a cartridge heater is inserted. The surface temperature is measured by
a miniature thermocouple tightly pressed onto the surface. The temperature
varies from room temperature to near the melting temperature of the droplet
material, or 232?C for pure tin. Droplets are generated and deposited in
a chamber which is constantly flushed with positive gauge pressure (34
kPa) of nitrogen gas to prevent oxidation.
The dynamic behavior of a droplet upon colliding with a subcooled
surface is recorded with a high speed video system (Kodak Ektapro EM, Model
1012) at a rate of 1000 frames per second. An image stored in the system
consists of 192 X 239 pixels. The illumination is provided by a stroboscope
which is synchronized with the camera, thus, very sharp images can to be
captured. The stored images in the digital memory are downloaded onto a
video tape using a S-VHS video tape recorder, and analyzed by an image
analysis software which is capable of measuring the dimensions of objects
by the number of pixels. An object of a known size (8 mm in diameter) is
recorded by the same video setup and used for calibration.
While this method makes use of millimeter-sized droplets, another
method is used to generate droplets with a diameter on the order of 100
µm. The second method utilizes the uniform droplet spray process
to produce microdroplets of a uniform size, velocity, and temperature.
The description of the droplet generation process is presented elsewhere
(Yim et al. 1996). Because the currently available imaging system is unable
to capture such a fast phenomenon as the impact of microdroplets, we observe
the final shapes of splats collected on solid surfaces. The surfaces of
the same materials used above, are heated in the same manner as described
in the first method. The experiments are performed in a nitrogen-flushed
atmosphere as well. The schematic of the method is illustrated in Fig.
4.2.
4.3. Results and discussion
4.3.1. Experimental observations
We first compare images of droplets colliding with solid surfaces
of different thermal states, as shown in Fig. 4.3. The fringe of the droplet
in Fig. 4.3 (a) is arrested due to solidification at approximately 2.9
ms after impact while the rest of molten volume recoils back to the center
until it completely freezes. On the other hand, the droplet in Fig.4.3
(b) shows a very vigorous oscillation upon colliding with the target, due
to the absence of solidification. The strong oscillation brings the droplet
back to its original spherical shape while lifting it into the air. In
other words, the image at 17.6 ms after impact, in Fig. 4.3 (b), looks
similar to an elastic solid ball bouncing off a solid wall. Fig.4.3 (c)
shows a transitional phenomena between (a) and (b): although the recoiling
of the droplet is more pronounced and lasts longer than (a), the droplet
fails to disengage from the surface due to freezing.
Next, we investigate the effect of droplet size on bouncing, which
is well pronounced in the impact of microdroplets. The small droplet of
Fig. 4.4 (a) bounces and creates a highly irregular shape of splats, while
the large droplet of Fig. 4.4 (b) forms a regular splat shape due to freezing
before bouncing. This result indicates that the role of droplet size should
be considered in addition to the thermal aspects to fully describe the
bouncing behavior.
In our experimental study, it was observed that droplets bounce
upon colliding with hot surfaces of all of the target materials except
tin. Figure 4.5 shows a very different behavior of molten tin droplets
upon colliding with a tin target. Although the dynamic and thermal states
of the droplet and the target satisfy the conditions for bouncing (see
below), the droplet does not bounce off the target of its own material.
We note that any liquid wets a solid of the same material. Therefore, this
result implies that good wetting between the droplet and the target surface
prevents bouncing.
The experimental observations described so far provide basic features
of the bouncing of molten metal droplets. In the following section, we
develop an approximate model which quantifies criteria to determine whether
the droplet bounces off or sticks to the target surface.
4.3.2. An approximate model
As observed above, molten tin droplets tend to bounce off solid
surfaces when oscillating violently upon colliding with the nonwetting
surfaces in the absence of solidification. If the heat loss to the subcooled
target surface is significant, solidification arrests the recoiling front
of the droplet, preventing it from bouncing. In addition, under certain
thermal conditions, only small droplets, which have a short oscillation
time, bounce while the larger ones do not. Based on these experimental
observations, we assume that the bouncing of molten droplets is dependent
upon the relative magnitudes of the oscillation and solidification times
in nonwetting conditions.
The period of the free oscillation of a liquid drop is used as
the oscillation time scale. Therefore, our oscillation time, 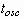 ,
is written as
,
is written as
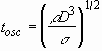 . (4.1)
. (4.1)
We note that the kinetic energy of the impacting
droplet affects the degree of bouncing. Schiaffino and Sonin (1997) observed
a mercury droplet colliding with glass fully disengage from the surface
when the Weber number exceeds 1.2. The Weber numbe is defined as 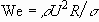 ,
where
,
where 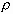 denotes the density,
denotes the density, 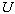 the impact velocity,
the impact velocity, 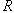 the
radius, and
the
radius, and 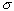 the surface
tension of the droplet. When the Weber number is smaller than 1.2, the
droplet does not completely detach from the surface. We assume that the
tin droplets have a similar Weber number to that of mercury for the disengagement
threshold. Since the impact inertia of the droplets used in our experiments
is well above unity, the bouncing always occurs in the nonwetting condition
when solidification is absent.
the surface
tension of the droplet. When the Weber number is smaller than 1.2, the
droplet does not completely detach from the surface. We assume that the
tin droplets have a similar Weber number to that of mercury for the disengagement
threshold. Since the impact inertia of the droplets used in our experiments
is well above unity, the bouncing always occurs in the nonwetting condition
when solidification is absent.
The solidification time is estimated by considering one dimensional
heat conduction from a molten droplet to a subcooled target solid. Carslaw
and Jaeger (1959) offered the analytical solution to the problem in which
two semi-infinite bodies of different temperature are in perfect contact
while one of them undergoes solidification. The solution considers the
superheat of the molten state and is able to obtain the exact thermal profile
inside a solidifying layer. We apply this model to obtain the approximate
solidification time of a droplet on a solid surface, and the schematic
of the problem is illustrated in Fig. 4.6. In the following, subscripts
1 and 2 denote target solid and droplet, respectively, and
superscripts s and l denote solid and liquid phase, respectively.
The thickness of a solidifying layer, 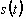 is given by
is given by
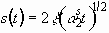 , (4.2)
, (4.2)
where 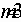 is the thermal
diffusivity of the solid state of the droplet, and t the time. A
parameter
is the thermal
diffusivity of the solid state of the droplet, and t the time. A
parameter 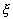 is determined
from the solution of the following:
is determined
from the solution of the following:
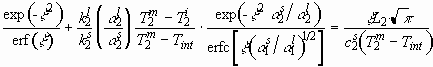 (4.3)
(4.3)
Furthermore, the interface temperature 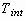 is obtained by using the following:
is obtained by using the following:
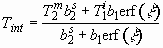 (4.4)
(4.4)
where the effusivity, b, is defined as 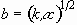 ,
whence
,
whence 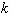 ,
, 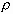 ,
and
,
and 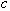 being the thermal
conductivity, density, and specific heat, respectively. The solidification
time is obtained by Eq. (4.2) after specifying the solidifying layer thickness,
s. Since we are interested in the solidification which hinders the
motion at the droplet fringe before bouncing, our characteristic solidification
thickness is assumed to scale as the hydrodynamic boundary layer thickness.
The boundary layer thickness,
being the thermal
conductivity, density, and specific heat, respectively. The solidification
time is obtained by Eq. (4.2) after specifying the solidifying layer thickness,
s. Since we are interested in the solidification which hinders the
motion at the droplet fringe before bouncing, our characteristic solidification
thickness is assumed to scale as the hydrodynamic boundary layer thickness.
The boundary layer thickness, 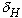 ,
is estimated by modeling the flow as one on an oscillating wall with the
period of
,
is estimated by modeling the flow as one on an oscillating wall with the
period of 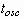 (Batchelor,
1967):
(Batchelor,
1967):
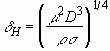 (4.5)
(4.5)
Therefore, our solidification time, 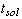 ,
is written as
,
is written as
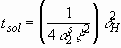 (4.6)
(4.6)
We predict that when the solidification time is longer than the
oscillation time, the droplet will bounce before its bottom gets arrested.
In the opposite case, the droplet will freeze at its bottom and get arrested,
failing to disengage from the target.
4.3.3. Regime map of droplet boucing
In this section, we provide experimental data on the bouncing behavior
obtained by varying the dynamic and thermal conditions of droplets and
target surfaces. The data are interpreted using our model presented above.
We calculate the oscillation and solidification times for each experimental
condition and predict whether the droplets will bounce or stick. It is
noted that our primary goal is to seek the existence of a trend which can
be explained in the frame of our model.
Table 4."complete-data" shows the conditions of all the experiments
whose results are presented in Fig. 4.7. Figure 4.7 (a) shows the data
collected by using nonwetting target surfaces. As predicted by our model,
when the oscillation time is short compared to the solidification time
(lower right portion of the graph), the droplets bounce off the target.
On the other hand, the droplets stick to the target when the oscillation
time is long compared to the solidification time. Seeking a threshold ratio
of the oscillation time to the solidification time which determines whether
the droplet will bouce or stick, we draw straight lines which enclose the
boundary dividing the bouncing and sticking regions. The slopes of the
straight lines correspond to the ratio of the two time scales, 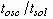 .
Our data show that when the time ratio is smaller than approximately 1.02,
the molten metal droplets bounce off the target surfaces. When the time
ratio is greater than approximately 1.05, the droplets stick to the targets.
The region between the two lines is considered where a transition from
bouncing to sticking occurs.
.
Our data show that when the time ratio is smaller than approximately 1.02,
the molten metal droplets bounce off the target surfaces. When the time
ratio is greater than approximately 1.05, the droplets stick to the targets.
The region between the two lines is considered where a transition from
bouncing to sticking occurs.
Figure 4.7 (b) shows the experimental results obtained by depositing
molten tin droplets on solid tin targets. The droplets stick to the target
even when the time ratio is significantly smaller than the threshold value.
This phenomenon is speculated to be caused by the strong wetting between
the droplet and the target surface. Based on this observation, we find
that the wetting or contact angle is an additional parameter which affects
the bouncing and sticking behavior of molten droplets. That is, it appears
that we can construct the regime map for bouncing and sticking using three
independent parameters, i.e. the solidification time, the oscillation time,
and the contact angle. However, we do not exclude the possibility that
the contact angle should play only minor role such that there exists a
threshold value under which strong wetting arrests the recoiling (as tin
droplet on tin target in our study), while over which value bouncing is
not greatly affected. A quantitave assessement of the effects of wetting
is not offered in this thesis, and further research on this subject is
strongly recommended.
4.5. Conclusions
In this chapter, the fundamentals of the bouncing behavior of molten
metal droplets are studied using experiments and an approximate model.
Two experimental methods are adopted. One uses molten tin droplets of milimeter
size generated by slow ejection of molten material. Images of droplets
bouncing or sticking upon colliding with various target conditions are
recorded using a high speed video system. The other method utilizes the
uniform droplet spray process to generate microdroplets and observation
of the final splat shapes, collected on various target conditions, is carried
out.
We interpret the experimental data based on the following assumption:
whether the droplet will bounce or stick is determined by the competition
between the relative magnitudes of the oscillation and solidification times.
We scale the oscillation time to the oscillation period of a free liquid
droplet. The solidification time is assumed to be the time it takes for
the hydrodynamic boundary layer to solidify. The heat transfer from the
droplet to the target is modeled by the heat conduction between two semi-infinite
bodies, one of which undergoes solidification.
An empirical regime map is constructed based on the two time scales
discussed above. We find a clear trend that the bouncing occurs when the
solidification is slow compared to the oscillation, while the sticking
is observed when the solidification is fast. Our experimental data suggest
that there exist threshold ratios of the two time scales which determine
whether the droplet will bounce or stick. The boundary appears to be nearly
linear, thus the ratios are almost constant, regardless of the droplet
sizes investigated in this study. We also find that bouncing is prohibited
by good wetting between the droplet and the target as well as by the solidification.
In other words, when the droplet and the target are of the same material,
no bouncing is observed even though when the solidification is fairly slow
compared to the oscillation, i.e., when the time ratio is well below the
threshold value, 1.02. This finding suggests the possible existence of
the third independent parameter, wetting, to affect the bouncing behavior.
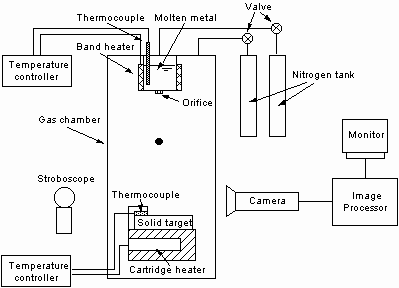
FIGURE 4.1. Experimental apparatus for the high
speed imaging of molten droplet impact.
FIGURE 4.3. (a) Images of molten tin droplets arrested
by solidification upon colliding with the aluminum 6061 surface. Original
droplet diameter = 1.57 mm, Impact velocity = 3.04 m/s, Droplet temperature
at impact = 261?C, Target temperature = 30?C. (b) Images of molten tin
droplets bouncing off the stainless steel 304 surface. Original droplet
diameter = 1.67 mm, Impact velocity = 3.08 m/s, Droplet temperature at
impact = 263?C, Target temperature = 195?C. (c) Images of molten tin droplets
colliding with the stainless steel 304 surface, showing the transitional
behavior. Original droplet diameter = 1.40 mm, Impact velocity = 2.91 m/s,
Droplet temperature at impact = 257?C, Target temperature = 183?C.
FIGURE 4.4. Micro tin droplets deposited on stainless
steel targets.
FIGURE 4.5. Micro tin droplets deposited on solid
tin targets.
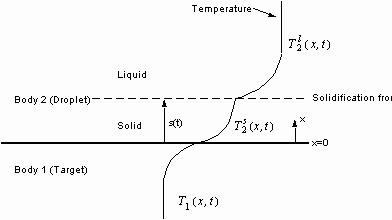 FIGURE 4.6. Geometry and temperature profile of
the solidification model.
FIGURE 4.6. Geometry and temperature profile of
the solidification model.
FIGURE 4.7. (a) Regime map of bouncing and sticking
on nonwetting surfaces. Squares and circles denote bouncing and sticking,
respectively. The slope is for the straight line in the linear scale. (b)
Sticking of tin droplets on tin targets.
CHAPTER 5
CONCLUSIONS
In this thesis, we have investigated the fundamental behavior of
liquid and molten metal droplets upon colliding with solid surfaces. Specifically,
we have examined physics behind splashing, post-impact oscillations, and
bouncing. The studies on these phenomena are expected to expand our knowledge
of the spreading behavior of liquid and molten droplets. In addition, the
results obtained in this work contribute to the search for the optimal
process conditions in the droplet-based manufacturing process.
First, we examined the fundamental mechanism that induces the splashing
of liquid droplets. In chapter 2, we developed a linear perturbation theory
of interface instabilities of a radially-expanding, liquid sheet in cylindrical
geometries. The theory was applied to the expanding sheet under a spreading
droplet to elucidate the origin of splashing. The base flow solutions were
estimated by using mass conservation. It was shown that significant deceleration
occurs in the early stages of spreading, which triggers the Rayleigh-Taylor
instability. The model supposes that the main factor inducing the deceleration
is not the viscosity but the continuity of flow around the impact region.
The theory was able to predict the most rapidly growing mode of azimuthal
disturbance and its growth rate at each instant during spreading. It was
found that the mode number of maximum instability changes because of time-dependent
coefficients in the amplitude equation. We examined the effects of several
parameters on the analysis results including the transient profile of an
interface radius, i.e. the coefficient A, the perturbation onset
time,  , and Weber number.
It was shown that larger impact inertia associated with higher We, and
thus presumably higher A, promotes interface instability and prefers
higher wave number for maximum instability.
, and Weber number.
It was shown that larger impact inertia associated with higher We, and
thus presumably higher A, promotes interface instability and prefers
higher wave number for maximum instability.
Chapter 3 investigated the oscillations of liquid droplets upon
colliding with solid surfaces. Our experiments showed that the droplets
with high impact inertia, associated with high We and Re, more vigorously
oscillate upon colliding with the solid surface. The oscillation was greatly
affected by the wetting between the liquid droplet and the solid surface.
Good wetting weakened and slowed down the recoilng process. Moreover, experiments
using droplets of different liquids and the same target solid showed the
strong effects of liquid properties and wetting behavior on the oscillation
phenomena. We developed a model based on the variational principle, assuming
the droplet shape as a cylinder. We also made modifications to the already
existing variational model which assumed the droplet shape as a truncated
sphere. Modeling results were in good agreement with experimental data,
showing the capability of our models to predict the complicated phenomena
of droplet spreading and recoiling. In addtion, the individual effects
of parameters such as We, Re, and the contact angle, was examined by using
our model. The analysis showed that the relative magnitudes of surface
energy and viscous dissipation play critical roles in determining droplet
dynamics. It was also shown that droplet dynamics are strongly affected
by the contact angle, e.g., poor wetting greatly promotes recoiling. A
significant computational effort was saved by solving a single second order,
nonlinear differential equation instead of solving the full Navier-Stokes
equation with the moving boundary. Furthermore, our current study showed
that use of the equilibrium contact angle yields the prediction sufficiently
close to the experimental measurements.
Bouncing of the molten metal droplets upon colliding with subcooled
target surfaces was studied in chapter 4. Experiments were performed with
various conditions to obtain the fundamental understanding of the bouncing
and sticking of molten droplets. We interpreted the experimental data based
on the following assumption: whether the droplet will bounce or stick is
determined by the competition between the relative magnitudes of the oscillation
and solidification times. An empirical regime map was constructed based
on these two time scales. We found a clear trend that bouncing occurs when
solidification is slow compared to oscillation, while sticking is observed
when the solidification is fast. Our experimental data suggested that there
exist threshold ratios of the two time scales which determine whether the
droplet will bounce or stick. The boundary appeared to be nearly linear,
thus the ratios were almost constant regardless of the droplet sizes investigated
in this study. We also found that the bouncing is prohibited by good wetting
between the droplet and the target, which suggests that wetting possess
finite degree of effects on the bouncing behavior.
In conclusion, the spreading behavior of molten metal droplets
in the inviscid, inertia-driven impact regime can be best explained by
examining the effects of factors such as We, Re, Oh, and contact angle.
To determine the optimal process conditions for the droplet-based manurfacturing
processes, it is necessary to understand the physical mechanisms that lead
to abnormal impact behavior such as splashing and bouncing. This thesis
offers physical models and experimental data to better control and prevent
such phenomena.
BIBLIOGRAPHY
Allen, R. F., 1975, "The role of surface tension in splashing,"
Journal of Colloid and Interface Sciece, vol. 51, p. 350
Baker, G. R., Meiron, D. I., and Orszag, S. A., 1984, "Boundary
integral methods for axisymmetric and three-dimensional Rayleigh-Taylor
instability problems," Physica D, vol. 12, p. 19
Batchelor, G. K., 1967, An Introduction to Fluid Dynamics,
Cambridge University Press, Cambridge, Great Britain
Bechtel, S. E., Bogy, D. B., and Talke, F. E., "Impact of liquid
drop agains a flat surface," 1981, IBM Journal of Research and Development,
vol. 25, p. 963
Bennett, T. and Poulikakos, D., 1993, "Splat-quench solidification:
estimating the maximum spreading of a droplet impacting a solid surface,"
Journal of Materials Science, vol. 28, p. 963
Berning, M. and Rubenchik, A. M., 1998, "A weakly nonlinear theory
for the dynamical Rayleigh-Taylor instability," Physics of Fluids,
vol. 10, p. 1564
Birkhoff, G., 1956, "Stability of spherical bubbles," Quarterly
of Applied Mathematics, vol. 13, p. 451
Bowden, F. P. and Field, J. E. 1964, "The brittle fracture of solids
by liquid impact, by solid impact, and by shock," Proceedings of the
Royal Society of London, A, vol. 282, p. 331
Brenner, M. P., Lohse, D., and Dupont, T. F., 1995, "Bubble shape
oscillations and the onset of sonoluminescence," Physical Review Letters,
vol. 75, p. 954
Carslaw, H. S. and Jaeger, J. C., 1959, Conduction of Heat in
Solids, 2nd Ed., Oxford University Press, Oxford, Great Britain
Chandra, S. and Avedisian, C. T., 1991, "On the collision of a
droplet with a solid surface," Proceedings of the Royal Society of London,
A, vol. 432, p. 13
Chandrasekhar, S., 1961, Hydrodynamic and Hydromagnetic Stability,
Oxford University Press, Oxford, Great Britain
Crandall, S. H., Karnopp, D. C., Kurtz, Jr., E. F., and Pridmore-Brown,
D. C., 1968, Dynamics of Mechanical and Electromechanical Systems,
Robert E. Krieger Publishing Co., Malrbar, FL
de Gennes, P. G., 1985, "Wetting: Statics and dynamics," Review
of Modern Physics, vol. 57, p. 827
Engel, O. G., 1955, "Waterdrop collisions with solid surfaces,"
Journal of Research of the National Bureau of Standards, vol. 54,
p. 281
Feng, Z. C. and Leal, L. G., 1997, "Nonlinear bubble dynamics,"
Annual Review of Fluid Mechanics, vol. 29, p. 201
Fukai, J., Shilba, Y., Yamamoto, T., Miyatake, O., Poulikakos,
D. , Megaridis, C. M., and Zhao, Z., 1995, "Wetting effects on the spreading
of a liquid droplet colliding with a flat surface: Experiment and modeling,"
Physics of Fluids, vol. 7, p. 236
Harlow, F. H. and Shannon, J. P., 1967, "The splash of a liquid
drop," Journal of Applied Physics, vol. 38, p. 3855
Hildebrand, F. B., 1976, Advanced Calculus for Applications,
2nd Ed., Prentice-Hall, Englewood Cliffs, New Jersey
Hilgenfeldt, S., Brenner, M. P., Grossmann, S., and Lohse, D.,
1998, "Analysis of Rayleigh-Plesset dynamics for sonoluminescing bubbles,"
Journal of Fluid Mechanics, vol. 365, p. 171
Inada, S., 1988, "Transient heat transfer from a free-falling molten
drop of lead to a cold plate," Journal of Chemical Engineering of Japan,
vol. 21, p. 583
Inada, S. and Yang, W.-J., 1994, "Solidification of molten metal
droplets impinging on a cold surface," Experimental Heat Transfer,
vol. 7, p. 93
Kendall, G. E. and Rohsenow, W. M., 1978, "Heat transfer to impacting
drops and post critical heat flux dispersed flow," Technical Report No.
85694-100, Department of Mechanical Engineering, Masschusetts Institute
of Technology, Cambridge, MA
Levin, Z. and Hobbs, P. V., 1971, "Splashing of water drops on
solid and wetted surfaces: hydrodynamic and charge separation," Philosophical
Transactions of the Royal Society of London, A, vol. 269, p. 555
Liu, H., Lavernia, E. J., Rangel, R. H., 1993, "Numerical simulation
of substrate impact and freezing of droplets in plasma spray processes,"
Journal of Physics, D, vol. 26, p. 1900
Liu, H., Lavernia, E. J., Rangel, R. H., 1994, "Numerical investigation
of micropore formation during substrate impact of molten droplets in plasma
spray processes," Atomization and Sprays, vol. 4, p. 369
Liu, H., Lavernia, E. J., Rangel, R. H., 1995, "Modeling of molten
droplet impingement on a non-flat surface," Acta Metallurgica et Materialia,
vol. 43, p. 2053
Madejski, J., 1976, "Solidification of droplets on a cold surface",
International Journal of Heat and Mass Transfer, vol. 19, p. 1009
Marmanis, H. and Thoroddsen, S. T., 1996, "Scaling of the fingering
pattern of an impacting drop," Physics of Fluids, vol. 8, p. 1344
Matson, D. M., Rolland, M., and Flemings, M. C., 1998, Solidification
1998, Edited by Marsh S.P., Dantzig, J. A., Trivedi, R., Hofmeister,
W., Chu, M. G., Lavernia, E. J., and Chun, J.-H., The Minerals, Metals
& Materials Society, p. 389
McPherson, R., 1981, "The relationship between the mechanism of
formation, microstructure and properties of plasma-sprayed coatings," Thin
Solid Films, vol. 83, p. 297
Menikoff, R., Mjolsness, R. C., Sharp, D. H., Zemach, C., and Doyle,
B. J., 1978, "Initial value problem for Rayleigh-Taylor instability of
viscous fluids," Physics of Fluids, vol. 21, p. 1674
Mundo, CHR., Sommerfield, M., and Tropea, C., 1995, "Droplet-wall
collisions: experimental studies of the deformation and breakup process,"
International Journal of Multiphase Flow, vol. 21, p. 151
Nakamura, S., 1991, Applied Numerical Methods with Software,
Prentice-Hall, Englewood Cliffs, New Jersey
Pasandideh-Fard, M., Qiao, S., Chandra, S., and Mostaghimi, J.,
1996, "Capillary effects during droplet impact on a solid surface," Physics
of Fluids, vol. 8, p. 650
Pasandideh-Fard, M., Bhola, R., Chandra, S., and Mostaghimi, J.,
1998, "Deposition of tin droplets on a steel plate: simulations and experiments,"
International Journal of Heat and Mass Transfer, vol. 41, p. 2929
Plesset, M. S., 1954, "On the stability of fluid flows with spherical
symmetry," Journal of Applied Physics, vol. 25, p. 96
Plesset, M. S. and Mitchell, T. P., 1956, "On the stability of
the spherical shape of a vapor cavity in a liquid," Quarterly of Applied
Mathematics, vol. 13, p. 419
Plesset, M. S. and Prosperetti, A., 1977, "Bubble Dynamics and
Cavitation," Annual Review of Fluid Mechanics, vol. 9, p. 145
Rayleigh, Lord, 1879, "On the capillary phenomena of jets," Proceedings
of the Royal Society of London, vol. 29, p. 71
San Marchi, C., Liu, H., Lavernia, E. J., Rangel, R. H., Sickinger,
A., and Muehlberger, E., 1993, "Numerical analysis of the deformation and
solidification of a single droplet impinging onto a flat substrate," Journal
of Materials Science, vol. 28, p. 3313
Schiaffino, S., 1996, "The fundamentals of molten microdrop deposition
and solidification," Ph.D. Thesis, Department of Mechanical Engineering,
Massachusetts Institute of Technology, Cambridge, Massachusetts
Schiaffino, S. and Sonin, A. A., 1997, "Molten droplet deposition
and solidification at low Weber numbers," Physics of Fluids, vol.
9, p. 3172
Shi, H.-H. and Dear J. P., 1992, "Oblique high-speed liquid-solid
impact," JSME International Journal, I, vol. 35, p. 285
Solonenko, O. P., Ushio, M., and Ohmori, A., 1994, "The complex
study of "metal drop-substrate" interaction," Proceedings of International
Seminar ISECTA '93, Almaty, Kazakhstan, p. 319
Stow, C. D. and Hadfield, M. G., 1981, "An experimental investigation
of fluid flow resulting from the impact of a water drop with an unyielding
dry surface," Proceedings of the Royal Society of London, A, vol.
373, p. 419
Taylor, G. I., 1950, "The instability of liquid surfaces when accelerated
in a direction perpendicular to their planes. I," Proceedings of the
Royal Society of London, A, vol. 201, p. 192
Thoroddsen, S. T., and Sakakibara, J., 1998, "Evolution of the
fingering pattern of an impacting drop," Physics of Fluids, vol.
10, p. 1359
Trapaga, G. and Szekely, J. 1991, "Mathematical modeling of the
isothermal impingement of liquid droplets in spraying processes," Metallurgical
Transactions, B, vol. 22B, p. 901
Trapaga, G., Matthys, E. F., Valencia, J. J., and Szekely, J.,
1992, "Fluid flow, heat transfer, and solidification of molten metal droplets
impinging on substrates: comparison of numerical and experimental results,"
Metallurgical Transactions, B, vol. 23B, p. 701
Tryggvason, G., 1988, "Numerical simulations of the Rayleigh-Taylor
instability," Journal of Computational Physics, vol. 75, p. 253
Tsurutani, K., Yao, M., Senda, J., and Fujimoto, H., 1990, "Numerical
analysis of the deformation process of a droplet impinging upon a wall,"
JSME International Journal, II, vol. 33, p. 555
Waldvogel, J. M. and Poulikakos, D., 1997, "Solidification phenomena
in picoliter size solder droplet deposition on a composite substrate,"
International Journal of Heat and Mass Transfer, vol. 40, p. 295
Watanabe, T., Kuribayashi, I., Honda, T., and Kanzawa, A., 1992,
"Deformation and solidification of a droplet on a cold substrate," Chemical
Engineering Science, vol. 47, p. 3059
Wilkes, E. D. and Basaran, O. A., "Forced oscillations of pendant
(sessile) drops," 1997, Physics of Fluids, vol. 9, pp. 1512
Worthington, A. M., 1877a, "On the forms assumed by drops of liquid
falling on a horizontal plate," Proceedings of the Royal Society of
London, vol. 25, p. 261
Worthington, A. M., 1877b, "A second paper on the forms assumed
by drops of liquid falling on a horizontal plate," Proceedings of the
Royal Society of London, vol. 25, p. 498
Xiong, B., Megaridis, C. M., Poulikakos, D., Hoang, H., 1998, "An
investigation of key factors affecting solder microdroplet deposition,"
Journal of Heat Transfer, vol. 120, p. 259
Yim, P., Chun, J.-H., Ando, T., and Sikka, V. K., 1996, "Production
and characterization of mono-sized Sn-Pb alloy balls," International
Journal of Powder Metallurgy, vol. 32, p. 155
Zhang, X. and Basaran, O. A., 1997, "Dynamic surface tension effects
in impact of a drop with a solid surface," Journal of Colloid and Interface
Science, vol. 187, p. 166
APPENDICES
APPENDIX A. NONDIMENSIONAL QUANTITIES
The following gives the definitions of the nondimensional quantities
used in chapter 2. Note that all the asterisked symbols denote dimensional
quantities, whereas non-asterisked symbols are the corresponding nondimensional
quantities.
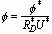
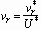
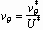
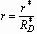
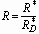
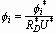 (
(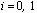 )
)
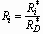 (
(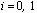 )
)
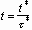
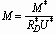
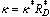
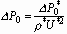
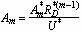
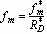
APPENDIX B. FREQUENCY OF PERTURBATIONS TO A CONSTANT
RADIUS LIQUID SHEET
In Chandrasekhar (1961), the frequency for the mth mode
azimuthal perturbation on a columnar liquid jet  is given by, in the present nondimensionalization,
is given by, in the present nondimensionalization,
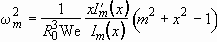 , (B1)
, (B1)
where 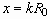 , k
denoting the wave number in z-direction, and
, k
denoting the wave number in z-direction, and 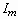 is the modified Bessel function of the first kind, of order m. We
show that for a two dimensional liquid sheet whose unperturbed radius
is the modified Bessel function of the first kind, of order m. We
show that for a two dimensional liquid sheet whose unperturbed radius 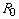 is kept unity, Eq. (B1) is reduced to Eq. (26). Using the following identities
(Hildebrand 1976):
is kept unity, Eq. (B1) is reduced to Eq. (26). Using the following identities
(Hildebrand 1976):
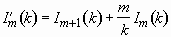 , (B2)
, (B2)
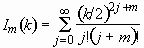 , (B3)
, (B3)
we find
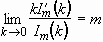 . (B4)
. (B4)
Therefore, in the limit  ,
Eq. (B1) is identical to Eq. (26).
,
Eq. (B1) is identical to Eq. (26).
APPENDIX D. MEASUREMENT OF EQUILIBRIUM CONTACT ANGLES
We use the sessile drop method to measure the equilibrium contact
angles between various liquids and solids. In this method, a small droplet
is placed on a solid surface and its contact angle is deduced by measuring
the base diameter and the height of the sessile drop. Assuming that the
sessile droplet takes a shape of a spherical cap, as shown in Figure D.1,
we obtain the following relation between the contact angle  and the height h and the base diameter
and the height h and the base diameter 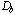 of the sessile droplet:
of the sessile droplet:
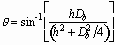 when
when  .
(D.1)
.
(D.1)
To take into account a slight deformation of the sessile droplet
of a finite volume due to gravity, measurements are made with droplets
of decreasing volumes and the equilibrium value is obtained by extrapolating
the data to zero volume (Schiaffino 1996). The volume of the droplet 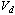 is given by
is given by
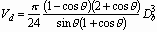 when
when  .
(D.2)
.
(D.2)
Table D.1 presents the measurement results.
TABLE D.1. Equilibrium contact angles
|
Liquid
|
Solid
|
Contact angle
|
|
Deionized water
|
Acrylic
|
87.4?
|
|
Deionized water
|
Silicon oxide
|
58.6?
|
|
Ink
|
Acrylic
|
70.9?
|
|
Ink
|
Silicon oxide
|
51.5?
|
|
Silicone oil
|
Acrylic
|
6.2?
|
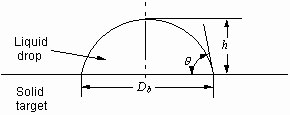
FIGURE D.1. Geometry of a sessile droplet of the spherical cap
shape
![]() is
displaced to
is
displaced to ![]() while the droplet descends with the speed of unity. The cylinder radius
while the droplet descends with the speed of unity. The cylinder radius ![]() is expressed as Eq. (23). (b)
is expressed as Eq. (23). (b) ![]() is the intersection radius of the target surface and the droplet traveling
with no deformation. 16
is the intersection radius of the target surface and the droplet traveling
with no deformation. 16
![]() .
(b) Corresponding deceleration. Note that the significant deceleration
is experienced by the interface immediately after impact, which drives
the Rayleigh-Taylor instability. 17
.
(b) Corresponding deceleration. Note that the significant deceleration
is experienced by the interface immediately after impact, which drives
the Rayleigh-Taylor instability. 17
![]() and
and ![]() . (a) The
coefficient a is given by
. (a) The
coefficient a is given by ![]() .
(b) The coefficient b vs. time for various wave numbers. 18
.
(b) The coefficient b vs. time for various wave numbers. 18
![]() .
(b) Temporal evolution of the shape amplitudes until
.
(b) Temporal evolution of the shape amplitudes until ![]() .
Initial conditions at
.
Initial conditions at ![]() are
are ![]() and
and ![]() .
The computation was performed for
.
The computation was performed for ![]() ,
, ![]() ,
and
,
and ![]() . Perturbations
of
. Perturbations
of ![]() are exceeded
by that of
are exceeded
by that of ![]() during
spreading. Perturbations of
during
spreading. Perturbations of ![]() decay after initially growing period. The perturbation amplitude of
decay after initially growing period. The perturbation amplitude of ![]() even decays to the value less than the initially assigned one before t
reaches
even decays to the value less than the initially assigned one before t
reaches ![]() . We define
a wave number, which is less than the so-found wave number by one, as a
pseudo-cutoff wave number - in this case, it is 55. 19
. We define
a wave number, which is less than the so-found wave number by one, as a
pseudo-cutoff wave number - in this case, it is 55. 19
![]() and
and ![]() . Initial
conditions for a dotted line are
. Initial
conditions for a dotted line are ![]() and
and ![]() . The computation
was performed for
. The computation
was performed for ![]() ,
, ![]() ,
and
,
and ![]() . (b) Changes
of a mode number of maximum instability and a pseudo-cutoff wave number
with time. Computation conditions are those of the solid lines in (a).
(c) Growth of azimuthal disturbances during spreading at the modes of maximum
instability. From the innermost corrugated circle,
. (b) Changes
of a mode number of maximum instability and a pseudo-cutoff wave number
with time. Computation conditions are those of the solid lines in (a).
(c) Growth of azimuthal disturbances during spreading at the modes of maximum
instability. From the innermost corrugated circle, ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() . Initial
conditions are
. Initial
conditions are ![]() and
and ![]() . The other
conditions are identical to those of (a). 20
. The other
conditions are identical to those of (a). 20
![]() on instability. (a) Wave number of maximum instability vs.
on instability. (a) Wave number of maximum instability vs. ![]() .
(b) Perturbation amplitude of those numbers vs.
.
(b) Perturbation amplitude of those numbers vs. ![]() .
23
.
23
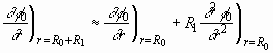 , (2.10)
, (2.10)
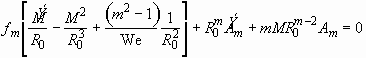 . (2.22)
. (2.22)
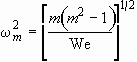 , (2.26)
, (2.26)
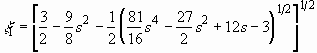 , (2.27)
, (2.27)


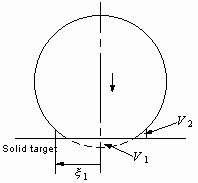

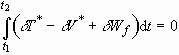 , (3.1)
, (3.1)
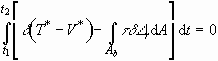 , (3.3)
, (3.3)
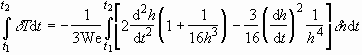 . (3.16)
. (3.16)
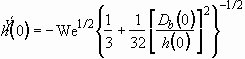 (3.25)
(3.25)
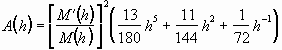 , (3.27)
, (3.27)
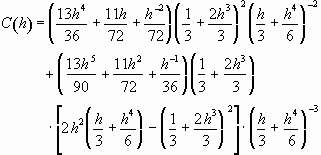 (3.29)
(3.29)

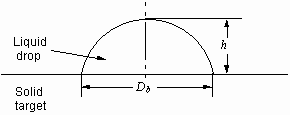

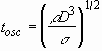 . (4.1)
. (4.1)
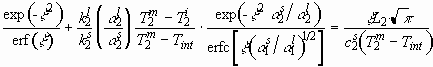 (4.3)
(4.3)
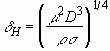 (4.5)
(4.5)


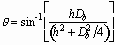 when
when 